A mirror gives light an extra twist

Chiral enantiomers—molecules that, like our left and right hands, are mirror images of each other but aren’t superimposable—are troublesome to differentiate. Identical in chemical formula, they behave interchangeably for the most part but distinguish themselves in the presence of other chiral molecules or fields.

Chiral enantiomers differ, for example, in how they interact with circularly polarized light (CPL). Like a screw, CPL’s polarization vector describes either a clockwise (right-handed) or counterclockwise (left-handed) helix in space; opposite-handed beams tend to veer in opposite directions as they refract through a chiral material. (See PHYSICS TODAY, December 2006, page 22 .)

Chiral molecules also absorb opposite-handed CPL at different rates. That difference is the basis for what’s known as circular dichroism (CD) spectroscopy. By measuring the dissymmetry factor, the difference between absorption rates of left- and right-handed CPL, normalized by the mean, scientists can discern the enantiomeric composition of, say, a biomolecule sample. But only a small fraction of absorption events—those due to coupling of electric- and magnetic-dipole forces—are chirality specific. Pure electric-dipole excitations occur far more frequently and with equal probability for left- and right-handed CPL. As a result, measured dissymmetry factors are rarely more than one part per thousand.

The relatively small contribution of chirality to absorption is partly the result of mismatched length scales. An optical field twists exactly once per wavelength—typically hundreds of nanometers—but biomolecules are often just a few nanometers across. At molecular scales, left- and right-handed CPL simply don’t look all that different.

Last year, Adam Cohen and his graduate student Yiqiao Tang, both at Harvard University, predicted that larger dissymmetries could be obtained using more contorted electromagnetic fields. ¹ They further noted that Maxwell’s equations should permit optical fields that are more contorted than CPL. Now, with a standard green laser, a mirror, and a glass coverslip, they’ve put their theory into practice. ²

Something from zilch

To start, Cohen and Tang wanted a way to describe not just whether a light field was left- or right-handed, but how much so. Adhering to basic symmetry constraints—chirality is time even, parity odd, and independent of orientation—they arrived at a quantity they termed optical chirality. Defined as [ε₀E · (∇ × E) + µ₀^-1B · (∇ × B)] / 2, where ε₀ and µ₀ are the vacuum permittivity and permeability, respectively, optical chirality is small for a gently twisted helix and large for a tightly twisted one.

As it turns out, the quantity isn’t new. Working at American Electronic Laboratories nearly a half-century ago, Daniel Lipkin described a property of electromagnetic fields that is conserved in a vacuum and “accompanies any circularly polarized wave,” and whose flow direction “reverses with the screw sense of the wave.” ³ The spatial density of that property—Lipkin termed it “zilch”—is Cohen and Tang’s optical chirality.

Lipkin and his contemporaries, concerned foremost with light in a vacuum, dismissed zilch as a curious but physically irrelevant property. Cohen and Tang’s theory suggests, however, that when light and matter interact, zilch is plenty meaningful. Specifically, the Harvard pair predicted that the dissymmetry factor of a chiral sample in an optical field should grow as the ratio of optical chirality to electric field intensity.

The theory’s first test came last year via experiments led by Malcolm Kadodwala of the University of Glasgow in the UK. ⁴ Kadodwala and company had fashioned spiraled gold nanostructures that exhibited plasmon resonances at optical frequencies. (For more on plasmonics, see the article by Mark Stockman, PHYSICS TODAY, February 2011, page 39 .) Laid flat on an insulating surface and irradiated with CPL, the plasmonic structures produced sharply contorted electric fields. In turn, dissymmetry factors for surface-adsorbed proteins were 10⁶ times larger than they were with CPL alone.

If Cohen and Tang’s model is correct, those increased dissymmetry factors should likely correspond to an increase in optical chirality. Adopting the pair’s definition, Kadodwala and company calculated that the plasmonic fields were about 10 times more chiral than the incident CPL beam—a large gain, but not large enough to explain the millionfold increase in dissymmetry. Explains Kadodwala, “We were perhaps running before we could walk. Our experimental system and our biomolecules were a bit complex for Cohen’s theory.”

Eccentricity, my dear Watson

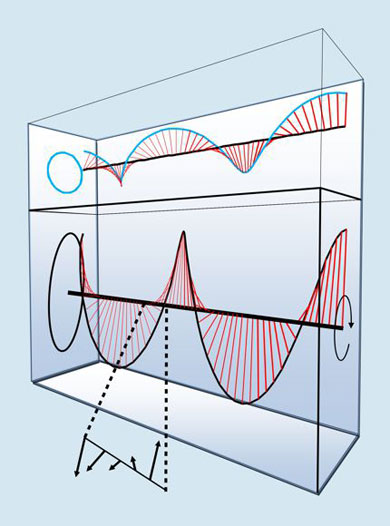
Cohen and Tang devised a simpler test: directing a beam of CPL at normal incidence toward a partially reflecting mirror. As illustrated in figure 1, the resulting interference should produce a wave that describes an elliptical helix in space and rotates circularly about the propagation axis with time. At each minimum in the electric field, the intensity diminishes but the optical chirality doesn’t, since the field’s orientation shifts dramatically in the regions nearby. The net effect, then, should be increased dissymmetry near those minima. The more eccentric the ellipse—that is, the more reflective the mirror—the greater the dissymmetry factor.

To test their idea, the researchers needed only to detect absorption rates for chiral material near one of the electric-field minima. That target region, however, is both very narrow—just a few nanometers wide—and very dim; the placement of the sample had to be precise and the absorption detection had to be sensitive.

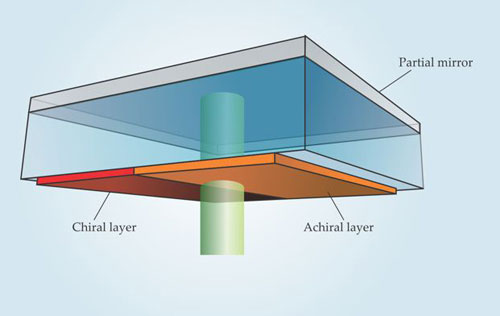
The team’s solution was to coat a glass coverslip with reflecting material on one side and a sample of fluorescent chiral molecules on the other, as illustrated in figure 2. The glass coverslip held the sample a fixed distance from the mirror, and its slight slant ensured that some parts of the sample lay near a minimum in the electric field. The tiny absorption rates could then be detected, by proxy of fluorescence, with a CCD camera.

Applied to a chiral, naphthalene-based compound, the scheme yielded a dissymmetry roughly 10 times that for plain CPL—a result that matched the team’s prediction to within 15%. The gain, however, comes at the cost of measurement precision. Says Cohen, “The energy density in the dim regions is so small that shot noise begins to drown out the signal. The more we enhance the dissymmetry, the noisier the signal.”

In fact, although the dissymmetry factor increased considerably, the measurement error grew in equal proportion. In part for that reason, Cohen says he’d “be surprised if this particular arrangement leads to better CD measurements. But we wanted to demonstrate the physical quantity, and these fields were simple enough to calculate with pencil and paper.”

Cohen hopes the work can help to put more complicated experiments on a sounder theoretical footing and aid in the design of more effective CD spectroscopy methods. Kadodwala, for one, is optimistic: “I’m convinced that these concepts will be a real boon for chiroptical spectroscopy.”