A leap in precision for diamond-defect NMR

Known for its noninvasiveness, NMR has long been a fixture in medicine, structural biology, and many other arenas. In conventional implementations, induction coils are used to detect magnetic signals generated when a sample’s nuclei, polarized by an external magnetic field, are manipulated with RF pulses. (See the article by Clare Grey and Robert Tycko, Physics Today, September 2009, page 44 .) But because nuclear spins polarize weakly—at room temperature, even a state-of-the-art magnet pulls only about 1 extra spin per 10 000 into alignment with its field—NMR doesn’t work well on tiny samples. A microliter (1 mm³) or more of material is typically required to produce a detectable signal.

Researchers have long sought to perform NMR spectroscopy at far smaller scales—on single biological cells, single proteins, even single atoms. To do so, they’ve proposed swapping out induction coils for more sensitive instruments: atomic-scale diamond defects known as nitrogen–vacancy (NV) centers.

In an NV center, two adjacent carbon atoms are replaced with a nitrogen atom and a vacancy. Isolated in the diamond lattice, the defect’s spin-1 electronic state is highly sensitive to external magnetic fields. NV centers can therefore serve as exquisite magnetometers, able to sense nanotesla fields generated by a sample at the crystal’s surface. (See the article by Lilian Childress, Ronald Walsworth, and Mikhail Lukin, Physics Today, October 2014, page 38 .) Conveniently, the defects fluoresce with a probability that depends on the spin state, so the magnetometer can be read out optically.

Over the past 10 years, researchers have made steady progress toward NV-center NMR spectroscopy. But they’ve struggled to achieve the spectral resolution necessary to tease out subtle frequency shifts in molecules’ NMR signals caused by nuclear interactions and shielding effects of electrons. Those shifts, known respectively as scalar couplings and chemical shifts, give a molecule its unique spectral fingerprint; if they’re unresolved, you can, for example, detect a hydrogen nucleus, but you can’t identify its host molecule.

Now a Harvard University team led by Ronald Walsworth, Mikhail Lukin, and Hongkun Park has demonstrated that with a clever measurement scheme and an appropriate sensor design, NV-center NMR can indeed resolve scalar couplings and chemical shifts. ¹ The sample volume need only be a few picoliters—about the size of a biological cell.

The lifetime problem

The Harvard team’s scheme is illustrated in figure 1. The sensor, a diamond implanted with a thin subsurface layer of NV centers, is topped with a small amount of liquid sample. A magnetic field B₀ polarizes the sample’s nuclear spins, and a subsequent RF pulse tips the spins into the transverse plane where they precess, generating an oscillating magnetic field.

Figure 1.

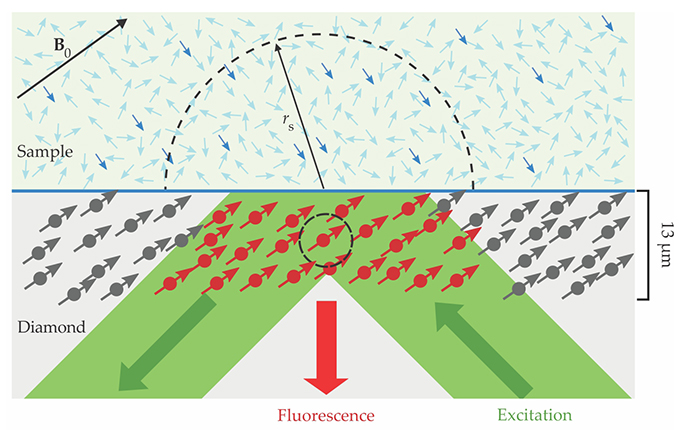
To detect that field, the researchers apply to the NV centers a magnetometry pulse sequence. An optical pulse initializes the NV centers in the |0⟩ electronic spin state, a microwave pulse tuned to a spin-state transition prepares them in a superposition of |0⟩ and |−1⟩ states, and—as the systems evolve—a train of so-called π pulses, applied at intervals τ, repeatedly flips their phase.

Provided the frequency f₀ = (2τ)⁻¹ associated with the phase flips differs from the frequency f of the precessing nuclear spins, the NV centers accumulate phase under the influence of the sample’s magnetic field. Finally, a microwave pulse “undoes” the superposition, yielding a population of |0⟩ and |−1⟩ states that depends on the total phase accumulated. That population can be inferred from the intensity of the defects’ fluorescence response to an optical readout pulse.

Similar approaches have been used to detect NMR signals from zeptoliter organic samples ² and even single proteins. ³ (See Physics Today, April 2013, page 12 .) But the spectral precision in those experiments wasn’t sharp enough to tease out molecular structure. That’s largely because spectral precision is determined by the measurement time, which, in turn, is limited by the NV center’s spin-state lifetime. Since that lifetime is a few milliseconds at best—much shorter than the NMR signal’s duration—the spectral resolution is typically just a few hundred hertz. Most scalar couplings, and many chemical shifts, become apparent only at resolutions of 10 Hz or better.

Three years ago Walsworth’s postdoc David Glenn thought of a way around the spin-lifetime problem: One could use an external clock to synchronize pulse sequences and make several measurements over the course of a single NMR signal; as long as all the magnetometry pulses are applied at some integer multiple of τ, the measurements can be stitched together into one high-precision measurement of the NMR signal, as illustrated in figure 2.

Figure 2.

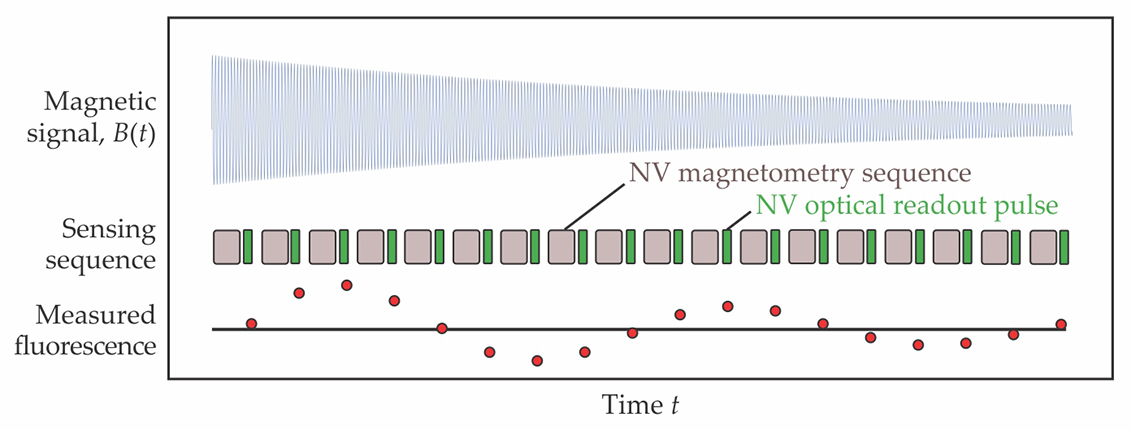
The Harvard researchers weren’t alone in noticing the virtues of synchronized measurement. Within a couple of years, two other teams had deployed similar synchronization schemes, ⁴ and a third had used quantum memories to extend NMR measurements beyond the NV center’s spin-state lifetime. ⁵ Those experiments refined the spectral precision of NV-center magnetometers to millihertz levels, well beyond the requirement for spectroscopy.

Still, linewidths in actual NV-center NMR experiments never budged below 10 hertz. No longer was it the NV magnetometers that limited spectral linewidths. It was the samples themselves.

The sample-size problem

In typical NV-center NMR experiments, the defects are embedded just a few nanometers below the diamond surface. Such shallow defects are sensitive primarily to the nuclear spins within a nanometer-scale hemispherical volume just above the surface. (Detection volume scales proportionally with depth.) The small volumes present complications: Diffusing molecules linger in the detectable region for just milliseconds before drifting away, molecules stuck to the diamond surface contribute an outsized share of the signal, and there are so few spins in the detection volume that random fluctuations can mask the magnetic-field-induced polarization. Collectively, those effects not only smear spectral lines but make them harder to detect.

To avoid those problems, the Harvard team buried its NV centers deeper than usual, in a layer about 13 µm thick. The resulting picoliter detection volumes yielded NMR signals with linewidths around a hertz, sharp enough to reveal scalar couplings and chemical shifts in all three organic molecules the group tested. Figure 3 shows an NMR spectrum, obtained under ambient conditions, of one of those molecules, para-xylene. The two peaks reflect the different chemical shifts associated with the molecule’s two distinct hydrogen positions—on the central benzene ring and in the electron-dense methyl groups; they are separated by just 20 hertz.

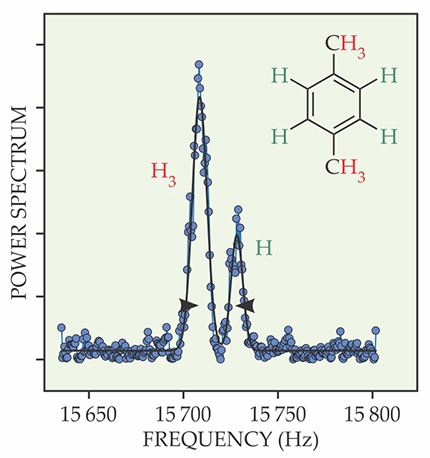
Figure 3.

“It’s quite a tour de force,” says Christian Degen, an experimentalist at ETH Zürich. “Different groups had been improving various aspects of NV-center NMR. It’s exciting to see someone put all the pieces together.”

The sensitivity problem

By increasing the detection volume, the Harvard researchers effectively traded spatial resolution for spectral resolution. That likely puts single-proton and single-protein NMR out of reach. But, says Walsworth, “at the micron scale, things are still very interesting. That’s the size of individual biological cells.”

Before Walsworth and his colleagues can extract meaningful spectra from living cells—or from more prosaic chemical species that are just hard to obtain in large quantities—they’ll need to improve their device’s sensitivity. So far, they’ve obtained results only from 100% pure samples, and even those require hours of signal averaging per spectrum.

Walsworth, however, sees plenty of room for improvement. “This was a skunkworks project,” he explains, noting that his team used a 50-year-old electromagnet, donated by Columbia University, to produce their 88 mT polarizing fields. With a stronger magnet and state-of-the-art microwave electronics to match, he says, the team could increase the field—and thus the measurement sensitivity—by orders of magnitude. Better diamonds, measurement protocols, and fluorescence detection schemes could boost sensitivity by an additional factor of 100.

The Harvard group is also exploring hyperpolarization techniques, which enhance a sample’s spin polarization by transferring spin from electrons, which polarize easily, to protons, which are more stubborn. (See Physics Today, June 1995, page 17 .) The effort to incorporate those techniques into NV-center experiments is still in the early goings, says Walsworth, “but we and many others have done the calculations, and they look very promising.”