When fermions become bosons: Pairing in ultracold gases
DOI: 10.1063/1.3001867
If you ask an undergraduate student, “What do neutron stars, metals, nuclei, and atoms have in common?” you might hear the answer, “They are made of neutrons, protons, quarks, and electrons.” While it is common for students to have heard about the existence of those microscopic particles and their individual properties like charge, spin, and color, it is far less common to hear from them that neutrons, protons, quarks, electrons, and atoms may exhibit a collective and macroscopic property called superfluidity, in which a large number of particles can flow coherently without any friction or dissipation of heat.
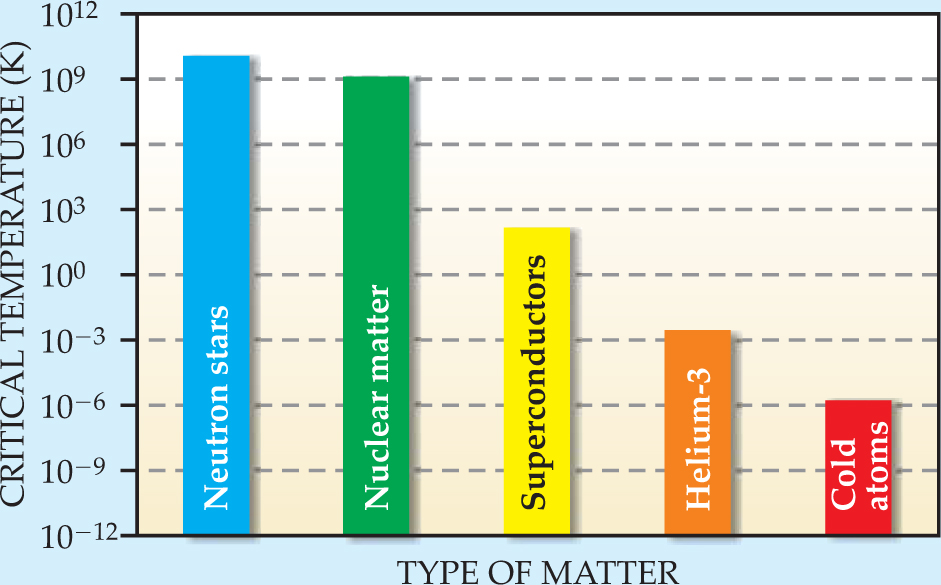
Neutron stars, metals, nuclei, and ultracold atoms have revealed their amazing superfluid state in ingenious experiments (see figure 1 for estimated critical temperatures of fermion superfluids). The first discovery of superfluid behavior was made nearly 100 years ago, when Heike Kamerlingh Onnes in 1911 cooled a metallic sample of mercury to temperatures below 4.2 K, using liquid helium-4 as the refrigerant, and found to his astonishment that the sample conducted electricity without dissipation. That dramatic drop in electrical resistivity to an essentially zero-resistance state was coined superconductivity, also known as charged superfluidity.

Figure 1. Fermionic superfluidity is a collective phenomenon found in neutron stars, nuclear matter, superconductors, liquid helium-3, and ultracold atoms, though they exhibit large differences in the critical temperature for the onset of superfluidity, as shown here. The key to their common behavior is the pairing of fermions to produce highly correlated fluids, which reveal themselves in several ways: They flow without dissipation, may exhibit an energy gap in the elementary excitation spectrum, have a nonclassical moment of inertia, and may exhibit vortex lattices upon rotation.
Revealed through Kamerlingh Onnes’s push to reach very low temperatures, that incredible quantum phenomenon emerged several years before the formulation of Schrödinger’s equation and the basic developments of quantum theory. It took nearly 50 years after the discovery of superconductivity for the development of a microscopic theory of the phenomenon. In the intervening years, many new superconductors (charged superfluids) were discovered, but only one neutral superfluid: liquid 4He.
Liquid helium-4: A boson superfluid
Although individual neutrons, protons, quarks, and electrons are all fermions with spin
The idea of boson condensation was put forth by Albert Einstein in 1924–25, after he had read and translated a paper by Satyendra Nath Bose on the statistics of photons and had extended Bose’s idea to the realm of massive bosons. 2 Einstein noted that a finite fraction (called the condensate fraction) of the total number of massive bosons would macroscopically occupy the lowest-energy (zero momentum) single-particle state at sufficiently low temperatures. For noninteracting bosons, the fraction of zero-momentum particles is 100% at zero temperature, but interactions in liquid 4He are sufficiently strong to reduce the condensate fraction to 10%, even at zero temperature.
Some microscopic understanding was developed by Nikolai Bogoliubov, who demonstrated that the excitation spectrum of a weakly interacting Bose gas is linear in the momentum of the excitation and that the critical velocity—the flow speed at which superfluidity is destroyed—is finite. Bogoliubov concluded that weak repulsive interactions do not destroy the Bose–Einstein condensate, and that an ideal Bose gas in its BEC phase has a vanishing critical velocity and thus is not a superfluid. Therefore, quite generally, the formation of a Bose–Einstein condensate does not guarantee superfluidity, which is associated with the existence of currents that flow without dissipation and requires correlations—that is, interactions—between bosons.
Superconductivity and the BCS theory
Drawing from the lessons of superfluid 4He and the connection to BEC, Max Schafroth proposed in 1954 that superconductivity in metals was due to the existence of a charged Bose gas of two-electron bound states—local fermion pairs—that condense below a critical temperature. However, experiments did not seem to support that simple picture. It was not until 1956 that a key idea emerged: Leon Cooper discovered that an arbitrarily small attractive interaction between two fermions (electrons) of opposite spins and opposite momenta in the presence of many others could lead to the formation of bound pairs. Since the pairing occurs in momentum space and the attraction between electrons is weak, the bound pairs, now known as Cooper pairs, are quite large and thus different from the local pairs envisioned by Schafroth. The origin of the glue between fermions was argued to be electron–phonon interactions, which could produce an effective attractive interaction between electrons that in turn could overcome their Coulomb repulsion.
The existence of a single fermion pair, however, was not sufficient to describe the macroscopic behavior of superconductors. It was still necessary to invent a collective and correlated state in which many fermion pairs acting together could produce a zero-resistance state. The invention of such a special state of matter occurred in 1957, when John Bardeen, Cooper, and Robert Schrieffer (BCS) proposed a many-particle wavefunction corresponding to largely overlapping fermion pairs with zero center-of-mass momentum, zero angular momentum (s-wave), and zero total spin (singlet). 3 As emphasized by BCS, their theory did not describe the picture proposed by Schafroth, Stuart Butler, and John Blatt, also in 1957, in which Bose molecules—local pairs of electrons with opposite spins—form an interacting charged Bose gas that condenses and becomes a superconductor. 4
One of the most fundamental features of the BCS state is the existence of correlations between fermion pairs, which lead to an order parameter for the superconducting state. In the original BCS work, the order parameter was found to be directly related to the energy gap E g in the elementary excitation spectrum. Since all relevant fermions participating in the ground state of an s-wave superconductor are paired, creating a single fermion excitation requires breaking a Cooper pair, but that costs energy. Thus the contribution of elementary excitations to the specific heat and other thermodynamic properties shows exponential behavior ~ exp(−E g/T) at low temperature T. Unlike the alternative theory of Bose molecules, the BCS theory was an immediate success, since it could explain many experimental results of the time at a quantitative level.
After its great success in describing superconductors (charged superfluids), the BCS theory was quickly generalized: to higher angular momentum pairing; to neutral superfluids such as liquid 3He (a fermion isotope of helium with two protons, one neutron, and two electrons), where spin-triplet p-wave superfluidity was found experimentally in the 1970s; and to pairing mechanisms beyond phonon mediation. But equally important were applications of the BCS theory to describe superfluid phases of fermions in nuclear matter and neutron stars, where nuclear forces provide the glue for fermion pairs. Glitches in the rotational periods of neutron stars have been attributed to the depinning of vortices—fundamental excitations of rotating superfluids—in the stars’ solid crust. For some nuclei, the energy gap in the elementary excitation spectrum and the nonclassical moment of inertia indicate the existence of a superfluid state.
Feshbach resonances
The evolution from a Bardeen-Cooper-Schrieffer superfluid to a Bose–Einstein condensation superfluid cannot be studied in neutron stars, nuclear matter, superconductors, or liquid helium-3, but in ultracold atoms it can be. Feshbach resonances are the tools that allow the interactions between atoms to be changed as a function of the applied magnetic field. The underlying requirement, shown schematically on the left, is that at zero magnetic field, the interatomic potentials of two atoms in their ground state (the so-called open channel) and in an excited state (the closed channel) be not too different in energy. The resonance, characterized by a divergence in the scattering length a s, occurs when the energy difference ΔE between a bound state with energy E res in the closed channel and the asymptotic, threshold energy E th of scattering states in the open channel is brought to zero by an applied external magnetic field B 0. For magnetic fields B close to B 0, the background scattering length a bg is renormalized to a s ≈ a bg[1 + ΔB/(B – B 0)], where ΔB is the width of the Feshbach resonance. When a bg is negative, a s is positive close to the resonance for magnetic fields smaller than B 0, as seen on the right, and two fermions can form Feshbach molecules of characteristic size a s. The most commonly studied Feshbach resonances for s-wave scattering occur at B 0 = 83.4 mT (834 gauss) for lithium-6 and at B 0 = 22.4 mT (224 gauss) for potassium-40, both stable fermionic isotopes.

From BCS to BEC superfluids
Although the BCS theory and its generalizations have found applications in several areas of physics where the mechanisms for fermion pairing are quite different, it is intrinsically a weak-attraction theory. Nature was very kind to the BCS theory because it saved some of its most precious Fermi superfluids to be discovered only in the mid-1980s (high-T c cuprate superconductors) and mid-2000s (ultracold lithium-6 and potassium-40 fermionic atoms), when strong deviations from BCS behavior were found. But prior to those experimental discoveries, a generalization of the BCS theory was slowly developed to encompass the strong-attraction regime in which fermion pairs become tightly bound diatomic Bose molecules and undergo Bose–Einstein condensation. The key question addressed theoretically was, Are the BCS and BEC theories the endpoints of a more general theory that connects Fermi superfluids to molecular Bose superfluids?
The simplest conceptual and physical picture of the evolution from BCS to BEC superfluidity for s-wave pairing can be constructed for low fermion densities and short-ranged interactions, for which the interaction range is much smaller than the average separation between fermions. In that limit the essence of the evolution at zero temperature is reflected in the ratio of the size of fermion pairs to the average separation between the fermions. In the BCS regime, the attraction is weak, the pairs are much larger than their average separation, and they overlap substantially. In the BEC regime, the attraction is strong, the pairs are much smaller than their average separation, and they overlap very little.
Amazingly, a clear picture of the BCS-to-BEC evolution at zero temperature didn’t emerge until 1980, when Anthony Leggett realized that the physics could be captured by a simple description in real space of paired fermions with opposite spins. 5 Leggett considered a zero-ranged attractive potential—that is, a contact interaction—between fermions and showed that when the attraction was weak, a BCS superfluid appeared, and when the attraction was strong, a BEC superfluid emerged. Philippe Nozières and Stephan Schmitt-Rink (NSR) used a diagrammatic method with a finite-ranged attraction to extend Leggett’s description to temperatures near the critical temperature for superfluidity. 6 Such ideas remained largely academic, however, since the evolution from the BCS to the BEC regime had not materialized in the experimental world.
But the discovery of cuprate high-T c superconductors in 1986 created a new paradigm for superconductivity. The BCS theory seemed to fail dramatically in some important regions of the phase diagram of cuprate superconductors, some of which have critical temperatures near 100 K. Motivated by the inapplicability of the BCS theory to cuprate superconductors, which seemed to have small electron pairs, Jan Engelbrecht, Mohit Randeria, and I extended the preliminary results of Leggett and NSR as an attempt to understand cuprates. 7 We used a zero-ranged attraction characterized by the experimentally measurable length scale a s, the so-called scattering length. The natural momentum scale is the Fermi wavenumber k F, and the strength of the attractive interactions can be described by the dimensionless scattering parameter 1/k F a s. That parameter changes sign in going from weak to strong attraction: The BCS weak-attraction limit is characterized by 1/k F a s ≪ −1; the BEC strong-attraction limit, by 1/k F a s ≫ +1. The crossover region between the two limits occurs for −1 < 1/k F a s < +1.
The phase diagram in figure 2 illustrates two important physical concepts of the evolution from BCS to BEC superfluidity. First, the normal state for weak attractions is a Fermi liquid, which evolves smoothly into a molecular Bose liquid. The two regimes are separated by a pair formation (or molecular dissociation) temperature T pair characterized by chemical equilibrium between bound fermion pairs and unbound fermions. Second, T pair and the critical temperature T c are essentially the same in the BCS limit: Pairs form and develop phase coherence (condense) at the same temperature. But in the BEC limit, fermion pairs (diatomic molecules) form first around T pair and condense at the much lower temperature T c = T BEC , where phase coherence is established.

Figure 2. Phase diagram for fermionic superfluids. To see the superfluid Bardeen-Cooper-Schrieffer or Bose–Einstein condensation phases for fermions, it is necessary to cool them to a small fraction of their Fermi temperature T F. When fermions pair to produce a superfluid state (yellow region), they exhibit two characteristic temperatures: the pairing temperature T pair (pink) at which fermion pairs first form and the critical temperature T c (blue) at which phase coherence between the pairs is established. In the BCS regime of large pairs and weak attraction, the two temperature scales are essentially the same. However, in the BEC regime of small pairs (diatomic molecules) and strong attraction, the two temperature scales are very different. The unitarity limit occurs when the scattering parameter 1/k F a s goes to zero, where k F is the Fermi wavenumber and a s is the scattering length, but the de facto separation between the BCS and BEC regimes is where the chemical potential μ goes to zero. (Adapted from ref.
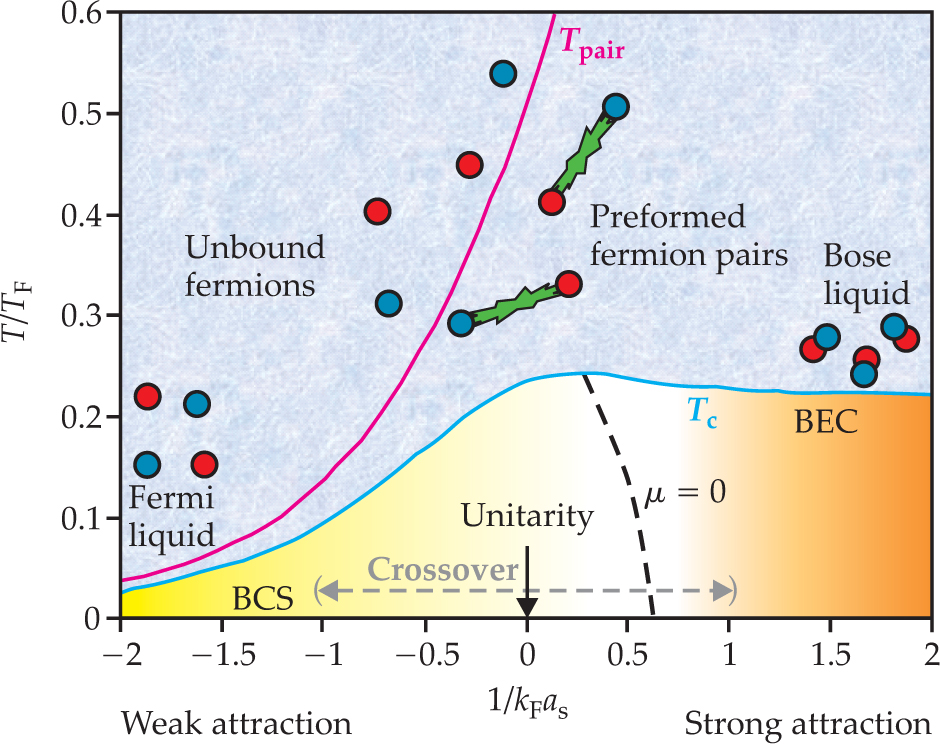
Two other concepts are shown in figure 2. First is the so-called unitarity limit, where the scattering length diverges. As the scattering parameter 1/k F a s changes sign from negative to positive, a two-body bound state with characteristic size equal to the scattering length emerges in vacuum (see the
Tuning the interactions
In superconductors some tunability of the fermion density can be achieved through chemical doping or electrostatic gating in the same material, and in liquid 3He some change in density is possible under pressure, but essentially no control over interactions is possible. In nuclei and neutron stars, the situation is even worse—there is no control at all over the density or interaction strength. But five years ago, the tuning of interactions became possible in ultracold Fermi atoms through magnetically driven Feshbach resonances (see the
In late 2003, almost simultaneously, three experimental groups succeeded in producing BEC of bound fermion molecules in optical traps at ultracold temperatures. Two groups, Rudolf Grimm’s at the University of Innsbruck
8
and Wolfgang Ketterle’s at MIT,
9
used 6Li atoms, and a third group, Deborah Jin’s at JILA,
10
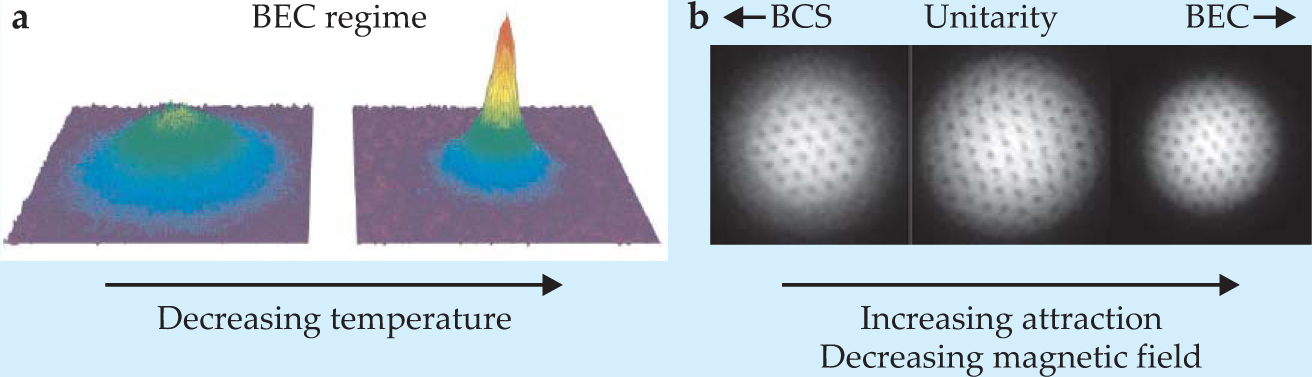
used 40K. Absorption images of the atoms after they were released from the trap showed a sharp central peak in the density (figure 3(a)), an important signature of the condensation of molecular bosons (that is, tightly paired fermions). But the true evidence for superfluidity was the experimental detection by the MIT group
11
of a vortex lattice in 6Li when the cloud of trapped fermions was first rotated and then allowed to expand (see figure

Figure 3. Evidence of superfluidity. (a) Two maps of the density of potassium-40 in the regime where the atoms form small fermion pairs, or molecular bosons. On the left, the temperature is above the critical temperature and the molecules are uncondensed. On the right, the temperature is below the critical temperature and the molecules undergo Bose–Einstein condensation, as evidenced by the sharp peak. (Adapted from ref.
Additional experimental developments at MIT 12 and Rice University 13 in 2005 initiated the study of Fermi systems (6Li) with population imbalance—that is, having unequal numbers of fermions in distinct hyperfine states, labeled “up” and “down.” Starting from an equal population mixture, appropriate application of RF pulses can arbitrarily change the relative populations by converting up fermions to down and vice versa. The ability to control the population of fermions and create imbalances varying almost continuously from equal mixtures to only one occupied state has stimulated substantial experimental and theoretical work to understand phase diagrams throughout the evolution from BCS to BEC superfluidity at zero and finite temperatures.
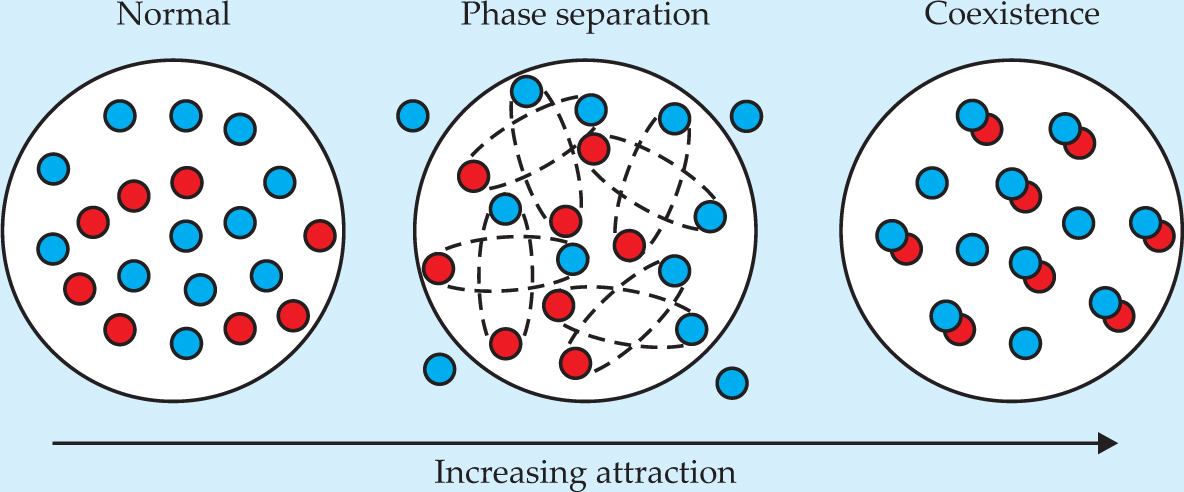
One expects a minimum of three phases when the population imbalance is fixed and the interaction is changed. As the interaction increases at zero temperature, the system is first a normal, unpaired fluid. It then separates into distinct regions, one containing a paired superfluid and the other containing excess unpaired fermions, before it finally reaches a phase in which the superfluid and excess fermions coexist (see figure 4). A key feature of the phases is that they are perfectly symmetric with respect to population imbalance, and it does not matter if the excess fermions are up or down, since atoms have the same mass.

Figure 4. Population imbalances, which can be created by applying RF pulses, can affect the superfluid state as it evolves from the Bardeen-Cooper-Schrieffer to the Bose–Einstein condensation regime. Some of the possible phases at zero temperature are illustrated here for an excess of “up” (blue) atoms. For a fixed and sufficiently large population imbalance the ground state of the system with weak attraction between the fermions is a normal mixture of unpaired “up” and “down” (red) atoms—they cannot overcome a pairing barrier created by their population imbalance. As the attraction increases, the blue and red atoms acquire enough energy to pair with each other but repel the excess atoms, which leads to phase separation between the superfluid’s paired fermions and excess, unpaired fermions. As the attraction between fermions is increased further, the pairs become more tightly bound and repel the excess atoms less; the result is a mixed state of coexisting superfluid and excess fermions.
The next frontiers
The unprecedented control and tunability in ultracold fermions may illuminate the physics of strongly correlated fermions in standard condensed-matter physics, nuclear physics, and astrophysics, where control is much more limited or nonexistent. Among the many possible experimental and theoretical directions, five are perhaps of the most immediate nature.
Mixtures of fermions of unequal masses. New possibilities arise when one considers mixtures of fermions of unequal masses, such as 6Li and 40K, 6Li and 87Sr, or 40K and 87Sr. Studying such mixtures is significant not only for atomic physics, but also for condensed-matter physics, where they could simulate fermions with different effective masses, and for quantum chromodynamics (QCD), where they could simulate mixtures of quarks with unequal masses. As in the case of equal masses, a minimum of three phases (normal, phase-separated, and coexisting) is expected for unequal masses throughout the evolution from BCS to BEC superfluidity. However, there is a dramatic asymmetry in the phase diagram of population imbalance versus interaction parameter.
Conceptually, the easiest limit to understand is the BEC regime of a mixture of equal numbers of up and down fermions. If their masses are different, they form heteronuclear diatomic molecules that repel each other weakly and produce a molecular BEC. When excess fermions are present, the paired fermions also repel the excess fermions, but the repulsion is smaller when lighter fermions are in excess, and larger when heavier fermions are in excess, which makes the coexistence region between pairs and lighter excess fermions larger than that of pairs and heavier excess fermions. That asymmetry awaits experimental confirmation, but two major experimental advances are narrowing the gap with theory: Quantum degenerate mixtures of 6Li and 40K have been created experimentally, 14 and Feshbach resonances that permit the control of interactions in such mixtures have been reported. 15
BCS-to-BEC evolution for higher angular-momentum pairing. Although the evolution from BCS to BEC superfluidity for s-wave pairing is fairly well understood theoretically and experimentally, there is no experimental realization of the phenomenon for p-wave pairing. Even though p-wave pairing has been extensively studied in connection with superfluid liquid 3He, some superconductors, and even neutron stars, most theoretical work has built on the BCS theory, under the assumption that the systems are somewhat weakly interacting. However, ultracold fermions like 6Li and 40K have some known p-wave Feshbach resonances between atoms in identical hyperfine states, and those may allow the tuning of p-wave interactions.
Although p-wave resonances are typically much narrower than s-wave and are much more difficult to study, they possess much richer physics due to their anisotropy. A simple conceptual example of that richness is the presence of an anisotropic elementary excitation spectrum that is gapless in the BCS regime but becomes fully gapped in the BEC regime. That evolution represents a phase change that is not accompanied by a change in the order-parameter symmetry (p-wave in both regimes), and thus it cannot be fully described by current theories of phase transitions. An experimental observation of the phenomenon would be a textbook example of the need for a new, generalized theory.
Effects of disorder in BCS-to-BEC evolution. Although disorder is difficult to control in standard condensed-matter systems, random potentials for trapped ultracold fermions can be produced under controlled circumstances. That allows the study of the effects of weak and strong disorder throughout the evolution from BCS to BEC superfluidity and the study of three-dimensional phase diagrams involving temperature, interaction, and disorder.
To give a sense of how rich that phase diagram can be, consider first a random potential that is independent of the hyperfine state of the atoms. Such a potential corresponds to the case of nonmagnetic impurities in standard condensed-matter systems. For an s-wave BCS superfluid, the amplitude and phase of the order parameter are strongly coupled, such that the breaking of Cooper pairs and destruction of phase coherence occur simultaneously. Because the random potential is not pair-breaking, it does not affect the phase coherence associated with the order parameter, and thus the critical temperature in the presence of weak disorder is essentially unchanged. The robustness of s-wave BCS superfluids with time-reversed fermion pairing (for example, pairs with opposite momenta and spin) in the presence of weak disorder was proposed nearly 50 years ago by Philip Anderson and is known as Anderson’s theorem. For weakly disordered BEC superfluids, in contrast, the breaking of local pairs and the loss of phase coherence occur at very different energy scales. The critical temperature is strongly affected by weak disorder, since phase coherence is more easily destroyed without the need to break local pairs simultaneously, and Anderson’s theorem doesn’t apply.
One can also study the phase diagram for s-wave superfluids in random potentials that are dependent on the hyperfine state of the atoms; such potentials simulate the effects of magnetic impurities in standard condensed matter. The effects of weak disorder in the BCS regime in this case are substantial, since the random potential is pair-breaking, which leads to the loss of phase coherence and to a quick suppression of T c . The T c reduction in the BEC regime is also strong, as with state-independent random potentials, since phase coherence is again quickly destroyed without pair breaking. However, the effects of strong disorder on superfluidity are more complex, thanks to disorder-induced localization—termed Anderson localization—of fermions in the normal state of the BCS regime and of bosons in the normal state of the BEC regime. The understanding of the normal and superfluid states in the strong-disorder limit throughout the evolution from BCS to BEC is still a theoretical challenge, but experimentalists may be able to reach that exciting regime in a controlled way and to study disorder-induced phase transitions.
Mixtures of fermions with three hyperfine states. Expanding the number of hyperfine states from two to three, which can be labeled red, blue, and green (or 1, 2, and 3), opens quite interesting possibilities, as there can be three types of s-wave pairings: red–blue, blue–green, and green–red. Such pairs may form a color superfluid with the coexistence of the three types of superfluids. That is analogous to a situation encountered in QCD in which quarks may pair in different color states in the cores of neutron stars and produce a color superconductor at densities several times larger than those found in typical nuclear matter (see figure 5(a)).

Figure 5. Simulating other systems. The ability to control interactions among ultracold fermions allows connections to be made with other areas of physics and may help address some of the key issues involving strongly correlated fermions in neutron stars, nuclei, and condensed matter. (a) Quarks of color quantum states red, blue, and green may pair at “low” temperatures and high densities, producing a color superconductor in the core of a neutron star. Color superconductivity might be simulated in ultracold Fermi atoms if a stable mixture of three hyperfine states for the same type of atom can be produced. (b) Cuprate superconductors, which have this complicated phase diagram, might be simulated by ultracold fermions in optical lattices. Although the temperature scales and the densities for ultracold atoms are much smaller than the corresponding temperatures and densities for color or cuprate superconductors, the ratios of the temperature to the Fermi temperature may be close, permitting some parallels to be drawn. It would be remarkable to achieve color superconductivity without quarks, and high-temperature superconductivity in a lattice without copper and oxygen.
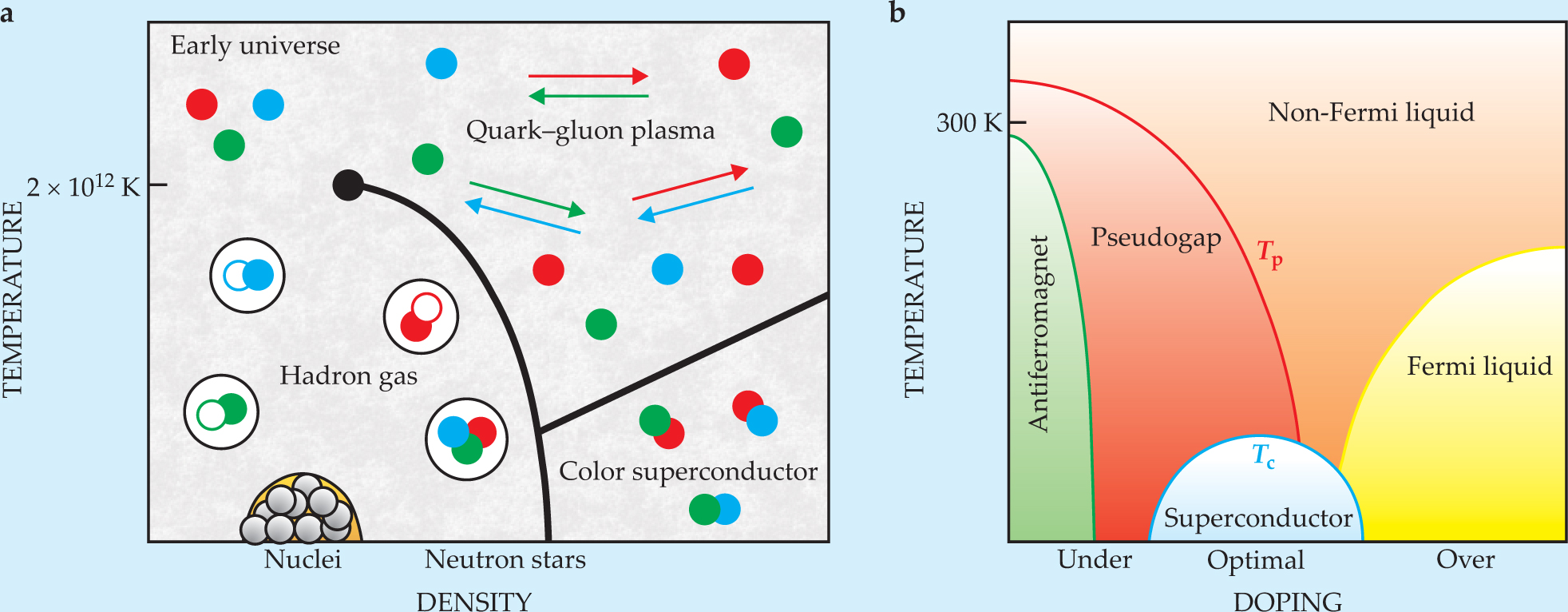
Important differences exist, however, between the color superconductor expected in QCD and the color superfluid expected in ultracold fermions. First, ultracold atoms are neutral and quarks are fractionally charged particles. Second, the densities of ultracold fermions are extremely low, while the densities for quarks are extremely high. Third, whereas quarks have a threefold degeneracy of their color, the degeneracy of hyperfine states in ultracold atoms is usually lifted by an external magnetic field. The need to control two-body collisions and prevent three-body collisions of trapped atoms involving three distinct hyperfine states makes experiments difficult, and color superfluidity has not yet materialized in ultracold fermions. Still, it is not crazy to think about it! A natural candidate for color superfluidity is 6Li, which has three hyperfine states that might be suitable, if losses can be cleverly controlled. Other ultracold fermions, including Fermi isotopes of ytterbium, are on the horizon. Furthermore, there is the promise of being able to control the interactions and populations of ultracold atoms to obtain and explore phases that do not yet have analogous behavior in QCD.
Ultracold fermions in optical lattices. The evolution from BCS to BEC superfluidity for s-wave systems in 3D cubic lattices was first discussed by NSR in 1985, but experiments probing superfluidity of ultracold fermions in optical lattices are just beginning. Tilman Esslinger and colleagues at ETH Zürich reported the production of 40K molecules in 3D cubic optical lattices using s-wave Feshbach resonances in early 2006,
16
but no evidence of a superfluid state was found until later that year, when Ketterle and coworkers loaded 6Li atoms in optical lattices and their pairs formed a condensate.
17
Those two experiments opened the door to studies of superfluid-to-insulator transitions in optical lattices and are likely to stimulate and renew the interest on the possible realization of d-wave superfluidity in nearly 2D lattices like those encountered in the high-T c cuprate superconductors, which have a complex phase diagram (see figure
Predicting the future
The unprecedented control over interactions in various dimensionalities and geometries has put research of ultracold fermions in harmonic traps and optical lattices at the forefront of investigations into the behavior of Fermi condensates and strongly interacting fermions. In particular, exotic phases of QCD, like color superconductivity, and superfluid phases in neutron stars and nuclear matter may have analogous counterparts in tabletop experiments involving ultracold fermions. Furthermore, studies of disorder-induced phenomena are also within experimental reach, and insights into p- and d-wave superconductivity found in condensed-matter physics are just around the corner, as ultracold fermions loaded into optical lattices begin to be explored. No one has a crystal ball to predict the future, but research on ultracold atoms will likely provide insight into the simulation and understanding of many known and unknown phases of nuclear, atomic, molecular, and condensed-matter physics.
I thank Sam Bader, Ian Spielman, Kris Helmerson, and Steve Anlage, among other colleagues, for reading this manuscript at various stages of its production and for their valuable suggestions. This article is dedicated to my father and mother, who passed away during its writing.
References
1. F. London, Nature 141, 643 (1938);https://doi.org/NATUAS
10.1038/141643a0
Phys. Rev. 54, 947 (1938).https://doi.org/PHRVAO10.1103/PhysRev.54.947 2. A. Einstein, Preuss. Akad. Wiss. Berlin Ber. 22, 261 (1924);
Preuss. Akad. Wiss. Berlin Ber. 23, 3 (1925);
S. N. Bose, Z. Phys. 26, 178 (1924).https://doi.org/ZEPYAA10.1007/BF01327326 3. J. Bardeen, L. N. Cooper, J. R. Schrieffer, Phys. Rev. 106, 162 (1957);https://doi.org/PHRVAO
10.1103/PhysRev.106.162
Phys. Rev. 108, 1175 (1957).https://doi.org/10.1103/PhysRev.108.11754. M. R. Schafroth, S. T. Butler, J. M. Blatt, Helv. Phys. Acta 30, 93 (1957).https://doi.org/HPACAK
5. A. J. Leggett, J. Phys. Colloq. 41, 7 (1980).https://doi.org/JPQCAK
10.1051/jphyscol:1980704 6. P. Nozières, S. Schmitt-Rink, J. Low Temp. Phys. 59, 195 (1985).https://doi.org/JLTPAC
10.1007/BF00683774 7. C. A. R. Sá de Melo, M. Randeria, J. R. Engelbrecht, Phys. Rev. Lett. 71, 3202 (1993).https://doi.org/PRLTAO
10.1103/PhysRevLett.71.3202 8. S. Jochim, M. Bartenstein, A. Altmeyer, G. Hendl, S. Riedl, C. Chin, J. Hecker Denschlag, R. Grimm, Science 302, 2101 (2003).https://doi.org/SCIEAS
10.1126/science.1093280 9. M. W. Zwierlein, C. A. Stan, C. H. Schunck, S. M. F. Raupach, S. Gupta, Z. Hadzibabic, W. Ketterle, Phys. Rev. Lett. 91, 250401 (2003).https://doi.org/PRLTAO
10.1103/PhysRevLett.91.250401 10. M. Greiner, C. A. Regal, D. S. Jin, Nature 426, 537 (2003).https://doi.org/NATUAS
10.1038/nature02199 11. M. W. Zwierlein, J. R. Abo-Shaeer, A. Schirotzek, C. H. Schunck, W. Ketterle, Nature 435, 1047 (2005).https://doi.org/NATUAS
10.1038/nature03858 12. M. W. Zwierlein, A. Schirotzek, C. H. Schunck, W. Ketterle, Science 311, 492 (2005).https://doi.org/SCIEAS
10.1126/science.1122318 13. G. B. Partridge, W. Li, R. I. Kamar, Y. Liao, R. G. Hulet, Science 311, 503 (2006).https://doi.org/SCIEAS
10.1126/science.1122876 14. M. Taglieber, A. C. Voigt, T. Aoki, T. W. Hänsch, K. Dieckmann, Phys. Rev. Lett. 100, 010401 (2008).https://doi.org/PRLTAO
10.1103/PhysRevLett.100.010401 15. E. Wille, F. M. Spiegelhalder, G. Kerner, D. Naik, A. Trenkwalder, G. Hendl, F. Schreck, R. Grimm, T. G. Tiecke, J. T. M. Walraven, S. J. J. M. F. Kokkelmans, E. Tiesinga, P. S. Julienne, Phys. Rev. Lett. 100, 053201 (2008).https://doi.org/PRLTAO
10.1103/PhysRevLett.100.053201 16. T. Stöferle, H. Moritz, K. Günter, M. Kühl, T. Esslinger, Phys. Rev. Lett. 96, 030401 (2006).https://doi.org/PRLTAO
10.1103/PhysRevLett.96.030401 17. J. K. Chin, D. E. Miller, Y. Liu, C. Stan, W. Setiawan, C. Sanner, K. Xu, W. Ketterle, Nature 443, 961 (2006).https://doi.org/NATUAS
10.1038/nature05224
More about the authors
Carlos Sá de Melo is a professor of physics at the Georgia Institute of Technology in Atlanta.
Carlos A. R. Sá de Melo, Georgia Institute of Technology, Atlanta, US .




