Ultrafast spectroscopy of quantum materials

Is “ultrafast spectroscopy of quantum materials” the winning square in Buzzword Bingo or a new area of scientific research that will advance the design and discovery of new materials? The recent developments described in this article point definitively to the latter. For decades, chemists and biologists have used light pulses with femtosecond durations to witness phenomena ranging from photodissociation to complex pathways in photosynthesis. Lately, an increasing number of researchers are directing ultrashort laser pulses at quantum materials—systems in which strong electron–electron and electron–lattice interactions lead to a multiplicity of competing phases, such as antiferromagnetism and superconductivity. Many physicists believe that ultrafast spectroscopic techniques will provide new insights into quantum materials by selectively exciting collective and single-particle modes of such phases and tracking in real time their subsequent decay pathways back to the ground state.

The union of the fields of ultrafast spectroscopy and quantum materials, though, has not always been a smooth one. For one thing, there is something of a culture clash in the style and personality of research in the two areas. Traditional experiments on quantum materials are performed in environmentally shielded, low-temperature laboratories that have the silent aura of a Carthusian monastery, while some laser labs are more reminiscent of a video-game arcade. In attempting to explain to low-temperature physicists what happens in our laser lab, I would often encounter the question, “So you take this crystal and blast it with a pulse of light?” However, as we will see, contemporary ultrafast optical experiments are far removed from indiscriminate blasting. Rapid developments in laser technology enable sensitive “weak-probe” measurements and experiments in which light is used to drive selective modes far from equilibrium.

Some historical perspective

Quantum materials is a label that has come to signify the area of condensed-matter physics formerly known as strongly correlated electronic systems. Although the field is broad, a unifying theme is the discovery and investigation of materials whose electronic properties cannot be understood with concepts from contemporary condensed-matter textbooks. Of those concepts, one of the most celebrated is Landau’s Fermi-liquid theory of the metals, which posits that the fundamental properties of the metallic state are the same as those of a system of noninteracting electrons, despite the presence of Coulomb forces between them.

Landau’s theory is based on the notion that the lowest-lying excitations above the metallic ground state are quasiparticles—quantum mechanical resonances that carry the same spin and charge as electrons, but with finite lifetime and enhanced effective mass. The ultimate message of Landau’s theory is that the ground state of strongly interacting fermions is limited to either liquid-like states that behave like noninteracting electrons or, if interactions are sufficiently strong, a state with spontaneously broken symmetry—for example, superconductivity or magnetism.

The remarkable properties of heavy-fermion materials ¹ epitomize Landau’s idea. In heavy-fermion metals, the conducting electrons interact strongly with a lattice of localized spins and would appear to be destined for some exotic phase at low temperature. However, it turns out that despite strong interactions between local and itinerant spins, the ground state is still a weakly interacting Fermi liquid, albeit one with an unseemly large enhancement of the quasiparticles’ mass that exceeds 10 000 in some cases.

The discovery of heavy-fermion systems in the late 1970s and early 1980s led to a pervasive notion that the Fermi-liquid ground state must be inevitable in metals that did not order—for example, in the configurations of their electrons’ charge or spin degrees of freedom. Although a profound idea, the message that materials with arbitrarily strong interactions manifest the same ground state as noninteracting electrons was not an especially inspiring one. In a classic case of an exception that proves the rule, the celebrated fractional quantum Hall effect (FQHE) was discovered at about the same time. The low-lying excitations of the FQHE state carry fractional charge and statistics, proving that emergent non-Fermi liquids could indeed exist. However, early demonstrations of the FQHE carried the implication that such states were to be found only under exotic conditions of ultrahigh mobility, reduced dimensionality, low temperature, and high magnetic field.

Thus the stage was set for the enormous psychological impact of high-T_c superconductivity in copper oxide materials. I recall sitting in a large auditorium at Bell Labs in Murray Hill, New Jersey, in 1988 as onstage Robert Cava and Bertram Batlogg connected a ceramic of yttrium barium copper oxide (YBCO) to a pair of electrodes and dunked the small puck-shaped object into liquid nitrogen. When the digital voltmeter’s LED readout counted down to 0.00000, indicating zero resistance, the reaction of the standing-room-only crowd was as if Elvis Presley had suddenly appeared from the wings.

What the assembled scientists were responding to was the sudden appearance of exotic quantum physics in a real material under conditions that, if not quite ambient, were not far from it. Within months, Philip Anderson set the agenda for the next quarter century of high-T_c research when he proposed that what was really special about the new superconductors was that their normal-state properties reflected a breakdown of the Landau paradigm. ²

Materials mash-up

Some of the most interesting quantum materials under investigation today were known 40 years ago. Although the materials were intriguing, they were also considered too messy to yield to fundamental understanding, an idea that echoed Wolfgang Pauli’s notorious warning not to work on dirty semiconductors. However, mess is in the eye of the beholder, and the urgency created by the discovery of high-T_c superconductivity in a complicated transition-metal oxide propelled many of us past our reluctance.

The ensuing years of research have shown that the apparent mess arises because competing spin, orbital, and lattice interactions yield a multiplicity of nearly degenerate ground states and complex phase diagrams. It has become increasingly clear that it is precisely in such systems—where complexity rules—that the most interesting and technologically important properties emerge. Competing interactions can enable a rapid transformation of a material from insulator to superconductor, or from magnet to paramagnet, in response to relatively weak external stimuli.

To convey the progress of decades of quantum materials research in a paragraph, I resort to the fictitious phase diagram of figure 1, which is a mash-up of salient features of systems such as heavy-fermion materials, copper oxide superconductors, and iron pnictide superconductors. The vertical axis represents temperature T, and although the horizontal axis represents charge-carrier concentration x, it could equally well stand for chemical potential, pressure, or magnetic field.

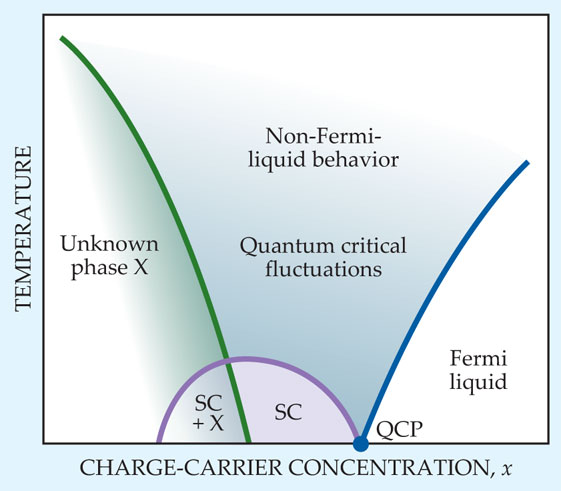
If we start a tour of the phase diagram at zero T and low x, we may encounter region “X,” a phase whose order parameter and symmetry are unknown (and exemplified by the pseudogap phase of the high-T_c cuprates). Moving on toward higher x, we find superconductivity together with some remnant of X; often no one knows whether the phases coexist spatially or are heterogeneous on mesoscopic length scales. Still further, superconductivity emerges as the dominant phase, only to disappear again at a quantum critical point (QCP), a continuous zero-temperature phase transition driven by variation of a parameter of the Hamiltonian (see the article by Subir Sachdev and Bernhard Keimer in Physics Today, February 2011, page 29 ). In the fan-shaped region above the QCP, raging fluctuations between phases may wipe out Landau’s quasiparticle resonances and, according to some, generate high-T_c superconductivity itself. At the highest carrier concentrations, Landau’s Fermi liquid may have dominion.

Ultrafast spectroscopy arrives

Around the time the first high-T_c superconductors were discovered in 1986, a revolution was occurring in the field of ultrafast optical spectroscopy. Rapid advances in laser technology allowed researchers to probe materials on time scales beyond the reach of broadband electronic instruments. Although the demonstration of pulses as short as 10 fs in the late 1980s was remarkable, the real revolution came from the low noise, stability, and turnkey operation of lasers based on solid-state media, such as titanium-doped sapphire. Quite suddenly, researchers could turn their attention from babysitting cranky dye lasers to addressing the complexity and subtlety of quantum materials phenomena.

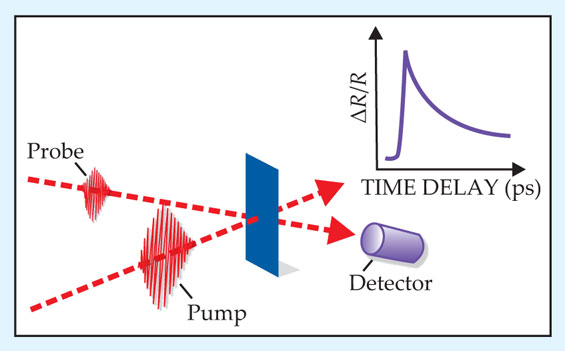
Figure 2 illustrates the simplest version of the pump–probe motif that is the basis for ultrafast spectroscopy. A beam of near-IR pulses from a Ti:sapphire laser is split in two: One beam photoexcites electrons in the lattice, and the other probes the induced transient changes in transmission or reflection. Before reaching the sample, the probe beam bounces off a movable mirror that provides a variable path length, and hence a time delay, relative to the absorption of the pump beam. Thanks to the stability of the Ti:sapphire laser, fractional changes in reflectivity, ΔR(t)⁄R, or transmission, ΔT(t)⁄T, of less than one part in a million can be time resolved on a femtosecond time scale.

Not only is that simple experiment powerful, it’s also the basis for more sophisticated techniques. For instance, rather than interrogate the sample at the photon energy of the Ti:sapphire laser itself (1.5 eV), the probe beam can first be directed to nonlinear optical crystals that provide far-IR (THz) pulses through optical rectification or UV pulses through harmonic generation. With a far-IR pulse, experiments can selectively probe low-energy modes, such as the superconducting energy gap, Josephson plasma resonances, or specific lattice vibrations. With UV pulses, the photoexcited state can be probed by angle-resolved photoemission, described in more detail below. The pump wavelength can be shifted as well, tuned so as to selectively excite specific modes of a material under study.

The appeal of those techniques made it inevitable that the lasers would be pointed at quantum materials. In the rest of this article, I describe examples of two classes of ultrafast optical experiments. In the first, the focus is on electrons excited above the energy gap that often accompanies the onset of ordered phases. In the second class, the goal is to manipulate the order parameter itself. Usually, photoexcitation weakens the degree of order, but for systems with coexisting and competing order parameters, one phase’s loss can be another’s gain.

Lessons from chemistry

Although measurements with resolution on electronic time scales were enabled by the remarkable Ti:sapphire laser, a pulse of visible light seemed to be a rather blunt instrument when unleashed on a correlated electron system such as a high-T_c superconductor. To skeptics, injecting photons, each delivering 1.5 eV of energy—a hundred times larger than the characteristic energy scale for superconductivity, k_BT_c—was like detonating a nuclear device in a public library reading room. Beginning in the early 1990s, though, a few believers began to aim their lasers at high-T_c superconductors. ³

Initial results showed that a phase transition to the superconducting state reveals itself in a small but clearly discernible ΔR signal. The fact that one can probe the onset of superconductivity in the near-IR evidently means that a quantum material such as YBCO changes color when it enters that state, although the 0.01% change in reflectivity of visible light is too subtle for the unaided eye. The mechanism for the color change in highly correlated superconductors remains a mystery and an active field of research to this day. ⁴

Whatever the underlying mechanism, reflectivity changes could be exploited to probe superconductivity on subpicosecond time scales. It was assumed, and later confirmed, that absorption of a 1.5-eV photon promotes an electron to a state high above the Fermi level, from which it decays rapidly by creating an avalanche of broken Cooper pairs (quasiparticles) and phonons. The ΔR(t) signal is then directly proportional to the nonequilibrium quasiparticle density, Δn(t).

To illustrate what can be learned from time-resolved measurements of Δn(t), consider a simpler system—a buffered solution of, for example, sodium chloride dissolved in water. By measuring ionic concentration as a function of temperature, one can determine the free-energy difference between dissociated NaCl and its crystalline phase. And yet such equilibrium measurements tell us nothing about the strength of the interaction between the ions in solution; that information is hidden in the kinetics of the reaction Na⁺ + Cl⁻ → NaCl.

The distinction between energetics and kinetics applies equally to superconductors, in which the role of solid NaCl is played by the condensate of Cooper-paired electrons; the solvated ions correspond to the gas of quasiparticles that coexists with the condensate. In equilibrium, quasiparticles evaporate from the condensate and, at the same rate, undergo the reverse process of recombining as quasiparticle pairs. When a quasiparticle pair jumps back into the condensate, its binding energy is released to the system. In conventional superconductors, that energy takes the form of a quantum of lattice vibrational energy, or phonon—the same excitation that provides the glue that binds electrons into Cooper pairs. In high-T_c materials, where the binding interaction is unknown, identifying the boson (or bosons) created by quasiparticle recombination is a tantalizing prospect.

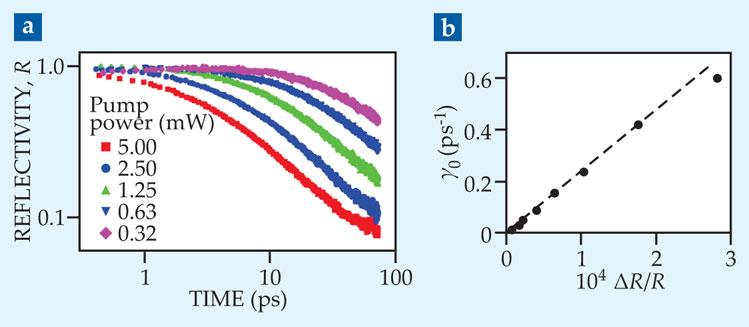
Figure 3 shows the change in reflectivity obtained from experiments that measure the kinetics of quasiparticle recombination.⁵ The data reveal that the analogy between quasiparticle dynamics and the reaction rates of physical chemistry is quite precise and quantitative. As discussed above, ΔR(t) is proportional to the photogenerated quasiparticle density, Δn(t). Each curve in figure 3a corresponds to a different laser power, which determines the number of excess quasiparticles immediately after photoexcitation, Δn(t = 0). When plotted on double logarithmic axes, the curves acquire a “knee” that shifts to shorter time delay as the initial quasiparticle concentration increases. The inverse of the time at which the knee occurs is the characteristic decay rate γ₀. Moreover, for times greater than 1/γ₀, the curves straighten out and become parallel, indicating a power law decay that is independent of Δn(t = 0). All those features of the data are predicted by a simple chemical rate equation, known as second-order kinetics, d/dt Δn(t) = −β[Δn(t)]², which describes a decay process requiring the interaction of a pair of particles.

The dreaded bottleneck

A seemingly paradoxical aspect of quasiparticle recombination in high-T_c superconductors is that the pair-wise kinetics are in accord with calculations based on Bardeen-Cooper-Schrieffer theory, ⁶ while results on more conventional superconductors are not. In fact, one of the puzzles that arose in studying superconductors that were known forty years ago was that the decay of a nonequilibrium quasiparticle population proceeded exponentially, rather than as a power law, and took a much longer time than predicted by BCS theory.

The apparent discrepancy was explained by Allen Rothwarf and B. N. Taylor, ⁷ who introduced the notion of a “phonon bottleneck” in 1967. According to BCS theory, when a quasiparticle pair reenters the condensate, its energy remains behind in the form of a newly created phonon. However, the leading cause of death of that phonon is the reverse process of decay into a quasiparticle pair. Thus conservation of energy locks the excess quasiparticle and phonon populations together, and the eventual return to equilibrium occurs only when the excess energy, or heat, propagates away from the photoexcited volume. As a result, measuring the return to equilibrium in a bottlenecked superconductor informs us only about rates of heat diffusion, while the underlying process of quasiparticle recombination remains hidden.

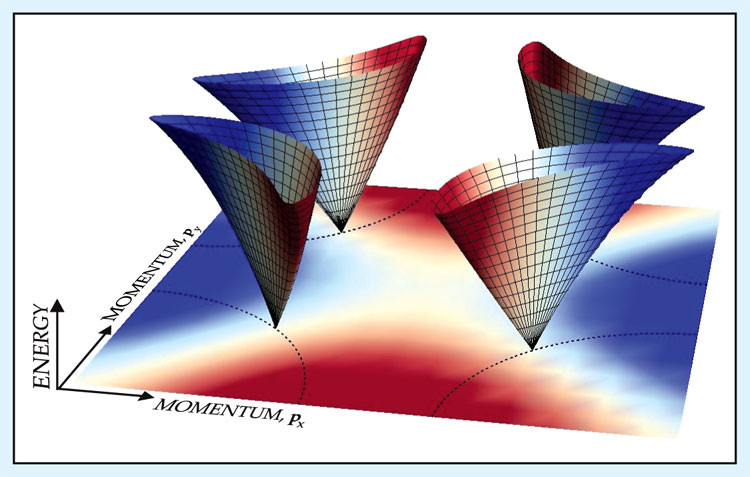
That explanation of quasiparticle kinetics in conventional superconductors raises the question of why the more revealing second-order kinetics of physical chemistry are observed in many high-T_c superconductors. The answer may lie in the fact that in quantum materials, more pathways are open to the decay of a quasiparticle pair than just the emission of a single phonon. Figure 4 is a visualization of the quasiparticle states in d-wave superconductors, such as the cuprates. Each horizontal cut through the curvy funnels is a contour of constant quasiparticle energy. At the bottom of each funnel is a nodal point, where the quasiparticle energy is zero. When high-energy (so-called antinodal) quasiparticles with momenta far from the node recombine, they can emit multiple low-energy quasiparticles. And just as shards of a shattered wine glass are unlikely to re-form, those low-energy quasiparticles will not regenerate the original quasiparticle pair. They thus defeat the bottleneck and restore the intrinsic second-order kinetics. ⁸

Taking a quasiparticle’s temperature

Does the experience of the high-energy antinodal quasiparticles differ from the ones near the bottom of the energy valleys? Because it averages over momentum space, IR reflectivity is blind to the distinction. But new methods, particularly the extension of angle-resolved photoelectron spectroscopy (ARPES) into the time domain, are helping to address the question.

Figure 5 shows the experimental setup for time-resolved ARPES. Samples are photoexcited with a pulse of 1.5-eV photons, and photoemission is induced by 6-eV photons generated by two stages of second-harmonic upconversion of pulses derived from the same laser used as a pump. ⁹ Excited-state electrons ejected from the surface are collected by a detector that measures their angle and kinetic energy distribution. From that information and the application of simple kinematic constraints, it is possible to infer the energy ε and momentum p of each electron before it is kicked out of the solid. Ultimately, the analysis leads to the determination of f(ε,t)A(p,ε,t), the product of the Fermi distribution function and the density of states at a time delay t after photoexcitation.

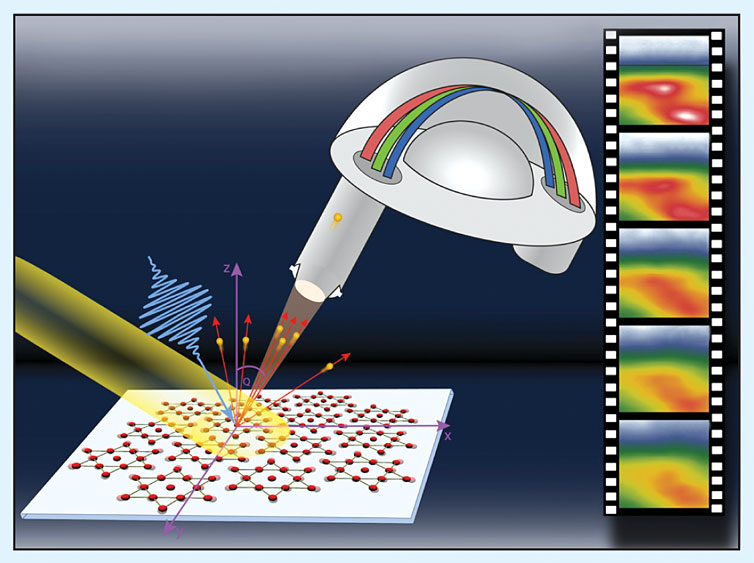
Five years ago Martin Wolf of the Free University of Berlin led a groundbreaking ARPES experiment to explore the near-nodal regions of momentum space in cuprate superconductors. ¹⁰ Along the nodal direction in momentum space, the density of states is essentially constant, and the photoemission intensity is directly proportional to f(ε,t). The sensitivity of the experiment is impressive, as the high-energy tail of the quasiparticle distribution function was measured down to one part in a thousand. Wolf and company observed that the occupation of states decays exponentially with energy; that is, f(ε,t) ∝ exp[−ε/k_BT_e(t)], where T_e(t) is the time-dependent nonequilibrium electronic temperature. By measuring the rate of cooling of the nodal quasiparticles, the researchers directly inferred the strength of their coupling to acoustic phonons.

The obvious next step is to map quasiparticle lifetimes as a function of their momentum. Unfortunately, it’s not currently possible to access the antinodal region with 6-eV photons generated from the Ti:sapphire laser. Nonetheless, studies looking as far from the node as possible with 6-eV photons are already revealing intriguing results. ^{11 , 12} Earlier this year, for example, a team of researchers from Lawrence Berkeley National Laboratory, led by Alessandra Lanzara, showed that quasiparticle lifetimes decrease rapidly with only a 20° deviation from the nodal direction, ¹² a measurement hinting that experiments may soon detect a resonant interaction with an as yet unidentified pathway for quasiparticle decay. The promise of such results has stimulated worldwide efforts to develop tunable pulsed sources, both laboratory- and synchrotron-based, that will capture the pathways of quasiparticle scattering and decay throughout momentum space.

Beyond quasiparticles: Manipulating order

As mentioned earlier, quantum materials are characterized by multiple, strongly interacting types of order. Although a single order parameter may dominate at any point in a material’s complex phase diagram, competing forms of order often lurk slightly higher in free energy. Ultrafast spectroscopy using a weak pump is emerging as a way to detect that competing order. At the same time, more intense pulses are being used to restructure the free-energy landscape, reshuffle the ranking of the various forms of order, and generate rapid switching from one to another.

Iron pnictide superconductors, the latest system to join the high-T_c family, provide a good example of a system whose competing order can be straightforwardly detected. ¹³ The phase diagram of the compound Ba_1−xK_xFe₂As₂ exemplifies the mash-up phase diagram of figure 1, except that the unknown phase X is actually known to be a metallic antiferromagnet (AF). At potassium concentrations near x = 0.2, the material enters the AF phase at 80 K and becomes a superconductor below a critical temperature of around 28 K.

Ultrafast spectroscopy reveals a photoinduced reflectivity change with two components that serve as markers for AF and superconducting (SC) order. The SC component increases rapidly upon cooling through T_c, as expected, but can still be seen in the normal state, which indicates the persistence of fluctuating SC order to more than twice T_c. A still more striking observation is that the AF component decreases just as fluctuating SC appears, an indication of competition between the two phases.

By stimulating quantum materials with higher-intensity laser pulses, researchers are moving to exploit such competition as a step toward manipulation and control. The most basic form of manipulation is photoinduced weakening of SC order. Dragan Mihailovic and coworkers at the Jozef Stefan Institute in Slovenia have investigated what happens when the energy delivered per pulse is increased beyond the linear response regime in a wide variety of superconducting materials. ¹⁴ For each system, they found a characteristic laser energy density at which the Cooper-pair condensate evaporates. Recent experiments on Nd_2−xCe_xCuO₄ have exploited that laser-induced suppression of superconductivity to enhance a mysterious form of order that exemplifies the unknown phase X in figure 1.

Weakening superconductivity with a laser is one thing, but strengthening it would be better. Last year researchers did just that in ultrafast optical experiments ¹⁵ on a very special member of the cuprate family, La_1.8−xEu_0.2Sr_xCuO₄ (LESCO). ¹⁶ In layered systems like the cuprates, superconductivity develops first in individual Cu-O atomic planes, with each plane described by a condensate wavefunction that has an amplitude and phase. In the typical cuprate, the onset of superconductivity in each layer is followed almost immediately by phase locking between adjacent planes, which yields a true, three-dimensional superconductor. But in LESCO (figure 6), 3D phase-locking requires cooling to 5 K, despite the fact that the individual planes become superconducting at 40 K. From the work of John Tranquada and collaborators,¹⁷ it’s clear that the simultaneous presence of stripe-like modulations of charge and spin density in the planes is somehow frustrating their natural tendency to phase lock.

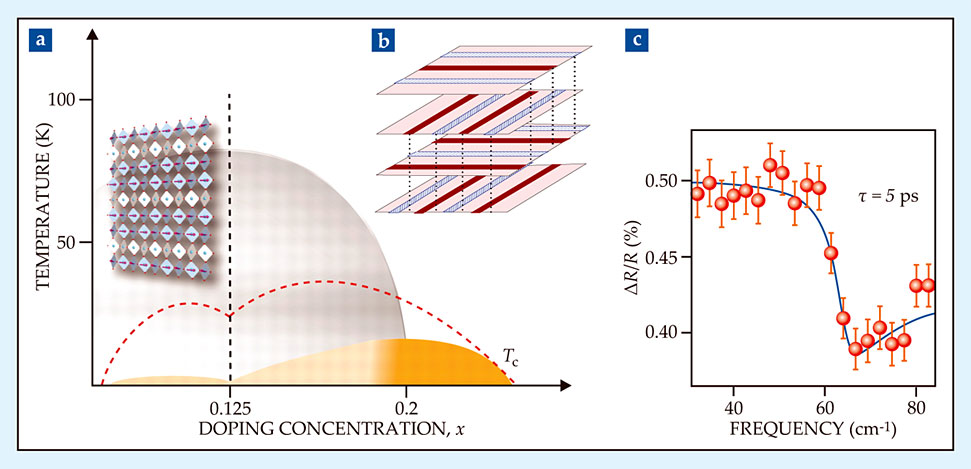
Rather than punish the frustrated superconductivity phase further with photoexcitation by near-IR 1.5-eV photons, Andrea Cavalleri and coworkers set out to encourage it with short pulses of mid-IR photons. That wavelength was chosen to resonate with in-plane Cu-O vibrational modes, and the researchers hypothesized that the resonance would weaken stripe order and relieve the interplane frustration. To detect photoinduced superconductivity, they tuned the probe wavelength to terahertz frequencies and searched for a particular mode—the so-called Josephson plasmon—that is the signature of phase coherence between planes. The spectrum in figure 6c shows the mode’s appearance as a plasma resonance in photoexcited LESCO. It is a demonstration that light has weakened stripe order and thus enabled the emergence of a 3D superconducting state.

A beautiful friendship

Although not necessarily love at first sight, the interaction of ultrafast spectroscopy and quantum materials research has blossomed into a vibrant branch of condensed-matter science. The basic pump–probe strategy is evolving rapidly toward selective excitations of well-defined modes using laboratory, linear accelerator, and synchrotron sources. On the probe side, spin- and angle-resolved photoemission, x-ray absorption, circular dichroism, and diffraction experiments are already yielding fascinating results. Thus it would seem that despite the initial clash of cultures, the fields of quantum materials and ultrafast spectroscopy are headed for that classic Hollywood ending—the start of a beautiful friendship.