Ultracold neutral plasmas
DOI: 10.1063/1.3366240
Plasmas are collections of charged particles that can exhibit an impressively diverse set of collective phenomena. They exist in an extraordinary variety of environments and span a great range of densities and temperatures, from 15 million kelvin in the core of the Sun to 200 K in the ionosphere and from 1030 particles per cubic centimeter in a white dwarf to 1 particle per cm3 in interstellar space. They can find application in lighting sources, manufacturing of computer chips, and fusion energy research. Plasmas created in the laboratory are used to replicate and study those that occur naturally and to probe the fundamental and complex behavior of plasmas.
Plasmas tend to be hot, because collisional energies of 1 eV or higher are required to ionize atoms and molecules. But in the past decade, a new laboratory plasma has emerged on the scene—the ultracold neutral plasma. With electron and ion temperatures as low as 1 K, ultracold neutral plasmas extend the temperature range of neutral and quasi-neutral plasmas by two orders of magnitude, and they allow researchers to explore the boundary between traditional plasmas and those in which spatial correlations and so-called strong coupling become important. Several surprising new phenomena have already been revealed. The low temperature and well-controlled creation process also allow experimenters to cleanly demonstrate classic phenomena of plasma physics, such as collective modes and thermalization.
As described in
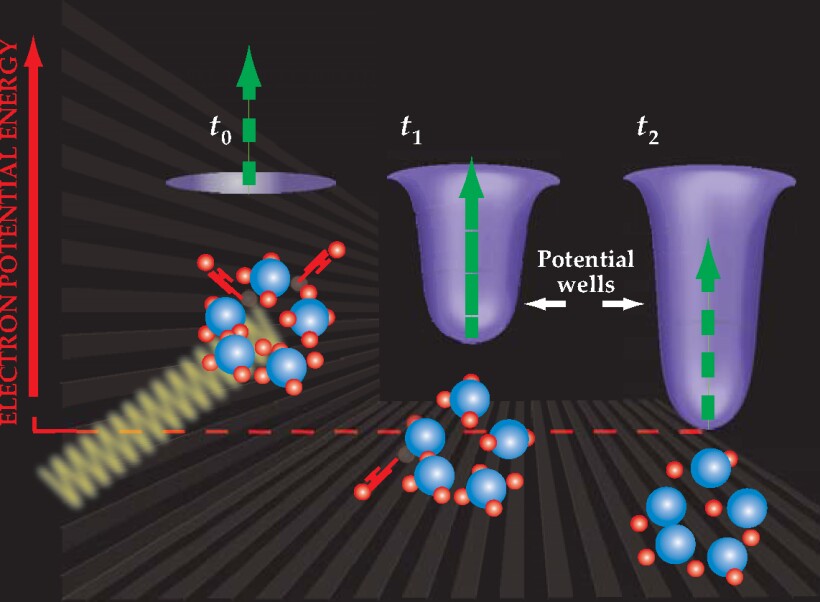
Box 1. How ultracold plasmas form
When a cloud of laser-cooled atoms is struck by a pulse of light tuned just above the ionization threshold (at t 0 in the figure), electrons are liberated from their atoms. From simple kinematics, the electrons carry almost all of the excess energy, which is typically 1-100 K but can be tuned as high as 1000 K. Even at 1 K, electrons have very high thermal velocity, so in the first few nanoseconds after the laser pulse, some electrons escape from the cloud. The remaining plasma has a slight positive charge, which creates a potential well (at t 1) that the next electrons must overcome if they are to escape.
As more electrons leave, the well gets deeper (t 2). When the well depth equals the kinetic energy of the electrons (which typically happens when a few percent of the electrons have escaped), the remaining electrons are unable to leave. Despite the plasma’s slight charge, researchers still call it a neutral plasma to distinguish it from plasmas containing only ions or only electrons. The ultracold plasma then expands at 50-100 m/s due to the outward pressure of the electrons on the ions.
Usual phenomena in an unusual plasma
Not every ionized gas is a plasma. Qualitatively, a system of charged particles becomes a plasma when collective motions and responses to external perturbations become organized and dominate over the behavior of individual particles. For example, charges in a plasma must be able to rearrange themselves to screen electric fields from penetrating significantly into the system. The length scale for screening is the Debye length,
Another characteristic of plasmas is a rich spectrum of collective modes, or wave motions. The first collective mode seen in an ultracold plasma (and the first collective mode presented in virtually every plasma physics textbook) was the Langmuir oscillation, an oscillation of the electron density at the electron plasma frequency. 1 The mode can be excited by an RF electric field, and as is common with plasmas, the excitation spectrum provides information about properties such as the electron density.
In a traditional plasma, electron-density oscillations such as the Langmuir oscillation are detected by inserting an electrical probe into the plasma. But that approach is practically impossible for ultracold systems, because the plasmas are so small and because heating would result from a connection to the outside environment. Langmuir oscillations are detected in ultracold plasmas by remotely collecting the electrons that escape from the plasma when energy is resonantly pumped into it.
The small plasma size and inhomogeneous density distribution were instrumental in the observation of collective modes beyond the fundamental Langmuir oscillations. In recent experiments by one of us (Rolston) and coworkers at the University of Maryland, a series of resonances were observed at radio frequencies above the Langmuir oscillation. We identified them as standing electron sound waves, similar to the so-called Tonks—Dattner resonances in traditional plasmas. Normally, and especially at low temperature, electron waves are local density oscillations and do not propagate like sound. But in the small ultracold plasma, the length scale of wave motion must also be small, which changes the oscillation into a sound wave. 2 In the usual Tonks-Dattner situation, the resonant mode frequencies and wavelengths are determined by an outer boundary such as the metallic wall that confines the plasma; the inner boundary is the point in the inhomogeneous density where the wave becomes evanescent and can no longer propagate. But in an ultracold plasma freely expanding into vacuum, there is no obvious outer turning point. An ad hoc choice of an outer turning point of three times the plasma root-mean-square size gave good agreement with a Tonks-Dattner model, but a rigorous description of the mode structure of such a boundaryless system is still an open problem.
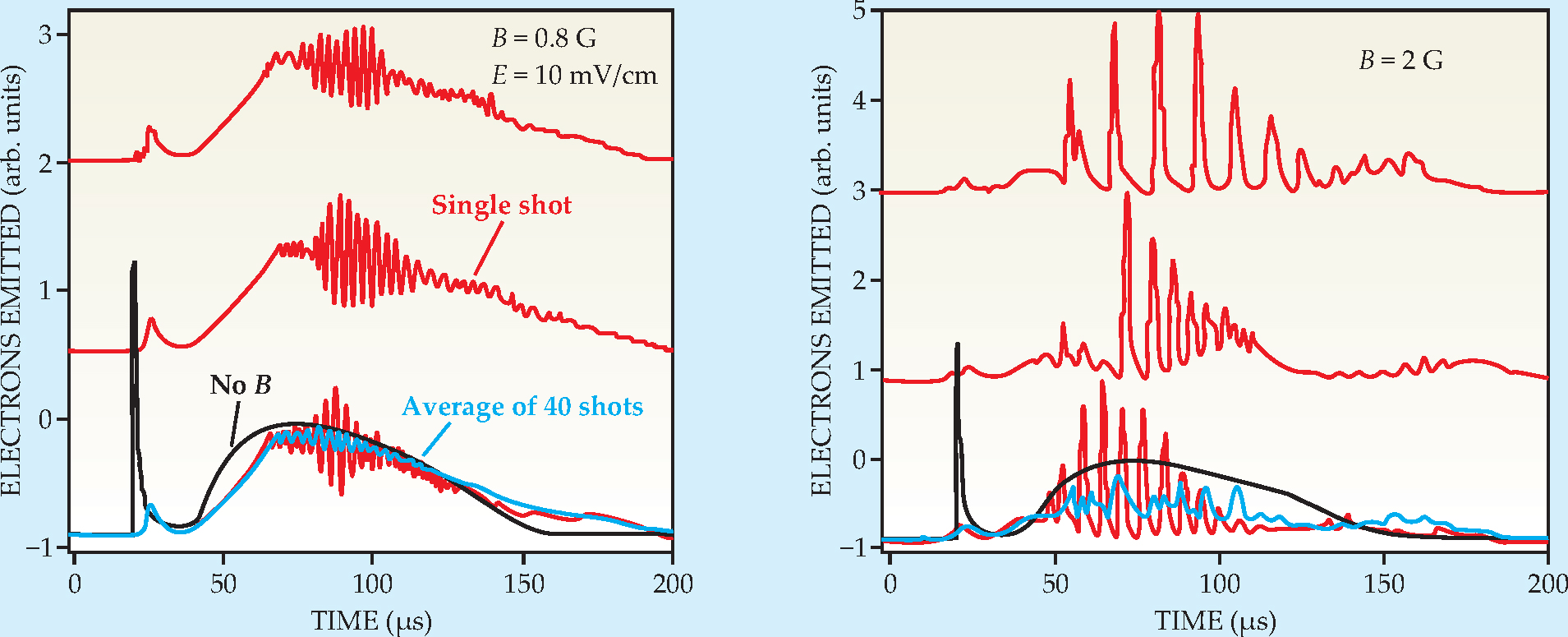
Collective modes in plasmas are often unstable. They can grow exponentially in oscillation amplitude until they become so large that they destroy the plasma or nonlinear effects start to limit the growth. In the pursuit of fusion power, instabilities can rob the plasma of the energy necessary for sustained fusion, so understanding, controlling, and eliminating them is critical. Ultracold plasmas also are susceptible to instabilities. In other work at the University of Maryland, an ultracold plasma subjected to crossed electric and magnetic fields emitted periodic bursts of electrons, as shown in figure 1. The cause of the bursts was identified as a high-frequency drift instability, in which harmonics of the cyclotron frequency couple to the electron motion driven by E x B drift. The magnetic field magnetizes the electrons, so that their cyclotron orbits are smaller than the plasma itself, and the dynamics are significantly altered. (The ions remain unmagnetized because they are so much more massive.) Because an ultracold plasma’s electrons have so little thermal energy, the fields necessary to see the instability are exceedingly small (1 G and 10 mV/cm) compared with those required for more energetic plasmas. The same instability also occurs in a plasma-based propulsion device called the Hall thruster, which has been used in hundreds of Russian spacecraft and is being evaluated as an option in US spacecraft. (See the Quick Study by Mark Cappelli, Physics Today, April 2009, page 76

Figure 1. An ultracold plasma instability. When an ultracold plasma is subjected to crossed electric and magnetic fields, E and B, it emits electrons not continuously but in pulses, a signature of a plasma instability. Each red curve (offset for clarity) is the signal from a single plasma realization, and the blue curves are averages over 40 realizations. Black curves show the typical smooth signal in no magnetic field.
Surprising connections between ultracold plasmas arise with rather disparate fields of physics. Several authors, such as Pierre Pillet and Daniel Comparat at the Laboratoire Aimé Cotton in Orsay, France, have pointed out the similarity between the dynamics of particles in an ultracold plasma and the dynamics of stars in a globular cluster. For example, recombination in ultracold plasmas—the collision of two electrons and one ion to yield an energetic electron and a bound, highly excited atom or molecule—is analogous to binary-star formation: Some binaries form through the interaction of three stars, with the extra body carrying away the binary binding energy. Care must be taken in both systems to describe dynamics on different time scales, because the motion of tightly bound pairs is much faster than the drift of individual particles. The thermodynamics of open systems also arises in both cases. Both the electrons in an ultracold plasma and the stars in a globular cluster are trapped in a potential well of finite depth. Thus neither system can achieve equilibrium, since collisions can always promote electrons or stars above the energy needed to escape. But the rate of escape eventually slows down, and a quasi-equilibrium state is established. The Michie—King distribution, which describes the velocities of stars in a cluster, has been suggested as the correct description for ultracold plasmas as well. 3 Ultracold plasmas offer the opportunity—unavailable in the study of galaxies—to probe the underlying physics through direct detection of the evaporating electrons and control of the confining potential.
Ultracold plasmas have also proven to be a good testing ground for molecular dynamics simulations. 4 – 6 Simulating any plasma is a difficult computational challenge, since the relevant time scales for motion of the ions and electrons can differ by six orders of magnitude. So far, full simulations have been able to capture only the first few hundred nanoseconds after plasma creation, during which local thermal equilibrium is established and recombination begins. To model physics at longer time scales, researchers must make approximations, such as treating electrons as a smooth neutralizing background for ions. But under that approximation, electron-ion collisions and recombination cannot be treated exactly. Since ultracold plasmas can be precisely controlled and accurately monitored, they can serve as benchmarks for molecular dynamics simulations. Computational methods that reproduce the data well can then be applied to more complicated systems, such as plasmas created by intense laser irradiation of solid targets, in which diagnostics are more challenging because of their fast collisional time scales.
Strong coupling
Most elementary plasma textbooks restrict their attentions to systems whose Debye lengths are larger than their typical interparticle spacings; that is, nλ D 3 > 1. The very idea of Debye shielding—that charges redistribute themselves to screen electric fields on the length scale of λ D —is hard to picture when the probability of finding any charge within a volume λ D 3 becomes small. The criterion nλ D 3 > 1 also ensures that charged-particle interactions are dominated by many weak interactions with far-away neighbors rather than isolated collisions between local pairs. The nature of the interactions has implications for the rate of collisional thermalization of a plasma out of equilibrium, which was described in seminal calculations by Lev Landau and Lyman Spitzer. 7
Box 2. Strongly coupled plasmas
The condition for strong coupling, nλ D 3 < 1, is mathematically equivalent, up to a constant of order unity, to the statement that the Coulomb interaction energy between neighboring particles exceeds the average kinetic energy, or that the coupling constant, the ratio of Coulomb energy to thermal energy, exceeds 1. (The coupling constant equals q 2/4πɛ0 akBT, where a = (3/4πn)1/3 is the Wigner-Seitz radius, q is the charge of each particle, and T is the temperature; for quantum-degenerate fermions, the thermal energy would be replaced with the Fermi energy.) Strongly coupled plasmas appear in extreme environments, such as the interiors of gas giant planets, white-dwarf stars, and matter irradiated with intense laser fields. They include dusty plasmas of highly charged macroscopic particles and nonneutral trapped ion plasmas that are laser cooled until they freeze into solidlike Wigner crystals (see Physics Today, September 1988, page 17

But when nλ D 3 < 1, the approximations normally used to describe Debye shielding and collisional thermalization become invalid. Many phenomena emerge that cannot be captured with standard theoretical tools, such as hydrodynamics and the Vlasov equations. Hydrodynamics treats the plasma as a continuous fluid, and the Vlasov equations describe the evolution of the plasma’s one-particle position and momentum distribution functions, neglecting binary collisions. Neither picture can describe the discreteness and strong, short-range interactions that are critical when λ D is smaller than the distance between particles.
Systems of charged particles with high density or low temperature can have nλ D 3 < 1 and still be plasmas in the sense that they are clearly dominated by collective behavior. Such plasmas are called “strongly coupled” because the Coulomb interaction energy between neighboring particles exceeds the average kinetic energy (a criterion equivalent to nλ D 3 < 1 up to a constant of order unity).
8
As a plasma becomes strongly coupled, spatial correlations develop between the particles, and the system can undergo a phase transition to a liquidlike or even solidlike state, as described in
Electrons in ultracold plasmas seem to remain weakly coupled, primarily because they are heated by recombination collisions. 9 The ions, however, start with much less energy and do not suffer from recombination heating, so they do cross into the strongly coupled regime.
Because ultracold plasmas are formed in a well-defined nonequilibrium state, they have been particularly useful for probing the way strongly coupled plasmas approach equilibrium. The results are applicable to other laser-produced plasmas, such as those formed by laser implosion of inertial confinement fusion pellets, which are so dense that their equilibration is difficult to study. In ultracold systems, strong coupling occurs at low density, which slows the equilibration time scale to a manageable few microseconds.
The first indication of previously unseen equilibration dynamics for ions in ultracold plasmas was a rapid heating in the first microsecond after photoionization reported independently by one of us (Killian) and by Scott Bergeson and coworkers at Brigham Young University. When ions are created, they inherit the spatial and velocity distributions from the very cold and essentially noninteracting neutral atoms. Ions have very little kinetic energy, but they have a large excess of potential energy because their spatial positions are completely uncorrelated: Some ions are created close to other ions, so they have a large Coulomb interaction energy. On a time scale of the inverse ion plasma frequency, about 1 µs, ions move under the influence of forces from nearby ions, short-range spatial correlations develop, and the ion spacing becomes more regular. Their potential energy decreases while their kinetic energy increases, raising the ion temperature by about 1 K.
That disorder-induced heating would be insignificant if the system were not strongly coupled, because the released potential energy would be negligible compared with the thermal energy. Disorder-induced heating also limits the minimum temperature, and thus the degree of coupling, that can be found in a laser-produced plasma after equilibrium. For ions in ultracold plasmas, the coupling constant, defined as the ratio of Coulomb energy to thermal energy (see
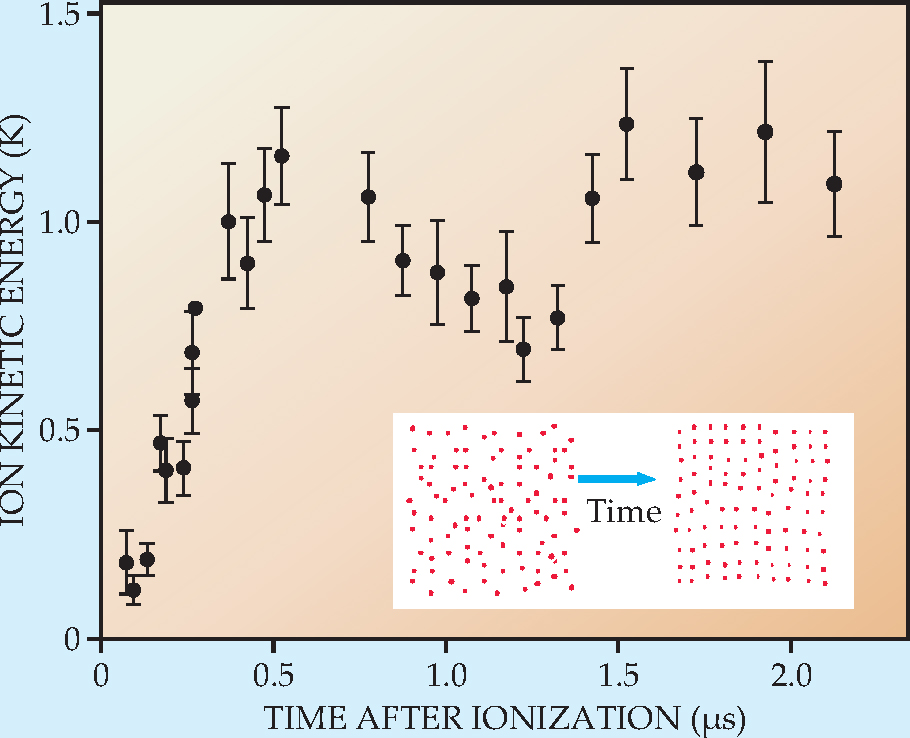
Close inspection of the data on disorder-induced heating reveals that the average kinetic energy overshoots and oscillates before settling into equilibrium, as shown in figure 1. That behavior is fundamentally different from the everyday experience with systems that are initially out of equilibrium, such as a cup of hot coffee left standing too long, in which the average kinetic energy monotonically approaches its limit. The unusual behavior of strongly coupled ultracold plasmas arises because each ion feels a caging potential from its neighbors, and it is probably not initially at that potential’s local minimum. As the ions settle into their wells, the whole system undergoes heavily damped but observable oscillations about equilibrium.
Why that phenomenon is not seen in other systems can be explained using language from statistical mechanics. The two-particle velocity distribution function, which embodies the correlation between the motion of one particle and that of its neighbors, usually equilibrates much faster than the single-particle velocity distribution function, which embodies the system’s temperature. That relationship is known as the Bogoliubov hierarchy, 10 and it greatly simplifies the statistical description of many-body systems. The condition for strong coupling in a Coulomb system is equivalent to the statement that the equilibration time scales have become equal, so a simplifying separation is no longer possible. In that sense, kinetic-energy oscillations are universal to equilibration in strongly coupled systems in which the plasma oscillation frequency is a universal time scale.
Studies of strong coupling in ultracold neutral plasmas complement work done on trapped nonneutral plasmas (see the article by Thomas O’Neil, Physics Today, February 1999, page 24
Rydberg atoms
In any plasma, atoms produced by three-body recombination collisions are formed in highly excited Rydberg states. And since the recombination rate scales as T -9/2, Rydberg atoms are copiously produced in ultracold plasmas. The energy carried away by the third body in the collision heats the plasma significantly, but the overall temperature evolution also depends on subsequent collisions between the Rydberg atoms and the plasma electrons, which can add or subtract thermal energy. The fate of any one Rydberg atom in an ultracold plasma is uncertain: It can be reionized, it can be driven to higher or lower principal quantum number through electron collisions, or it can radiatively decay to a more tightly bound state.
In fact, the distinction between a dense gas of cold Rydberg atoms and a plasma is tenuous. Researchers have discovered that dense clouds of Rydberg atoms—created by tuning the excitation laser from slightly above to slightly below the ionization threshold—spontaneously evolve into ultracold plasmas. Thomas Gallagher at the University of Virginia and Pillet and coworkers have shown that strong attractive interactions between the highly polarizable Rydberg atoms lead to ionizing collisions, which produce electrons that ionize other Rydberg atoms. Once electrons begin to get trapped by Coulomb attraction to the ions, they ionize even more atoms, and the resulting avalanche creates a plasma.
The avalanche ionization approach to forming an ultracold plasma has recently been applied to molecules—specifically, nitrogen monoxide molecules in a supersonic beam. 12 Such molecular plasmas are orders of magnitude more dense than those made from laser-cooled atoms. Their electrons, unlike those in atomic systems, appear to be cold enough (a few kelvin) to be strongly coupled, as estimated through plasma expansion studies. What exactly is different about the molecular plasma that allows strongly coupled electrons is an open question.
Antimatter plasmas
Most ultracold plasmas are produced by lasers. A notable exception is the antimatter plasmas at the heart of low-energy antihydrogen research. Precision tests of CPT symmetry (charge conjugation, parity, and time reversal) and the gravitational acceleration of antimatter require cold antihydrogen, preferably confined to a trap. To achieve that goal, experimenters at the antiproton decelerator facility at CERN capture antiprotons and positrons in separate Penning traps, in which they are subject to a large magnetic field (see the Quick Study by Gerald Gabrielse on
It was recognized in 1988 that three-body recombination, with its T-9/2 scaling, might be an efficient mechanism for antihydrogen formation in ultracold antimatter plasmas.
13
In 2002 two collaborations, ATHENA and ATRAP, observed low-energy antihydrogen. (Antihydrogen formed at high energies in a beam had been detected six years earlier.) ATHENA detected the antihydrogen from its annihilation on trap walls—neutral antihydrogen atoms are not confined by the fields of the Penning trap. (See Physics Today, November 2002, page 17
In zero field, recombination involves not a single collision but a series of collisions. An atom is formed with a small binding energy and is buffeted by electrons, which may reionize the atom or increase or decrease the binding energy. If the atom reaches a low enough principal quantum number, further collisions and radiation will probably drive it to the ground state. In a 5-T magnetic field, positrons are tightly bound to the magnetic field lines, and atoms that form are not the simple highly excited Bohr atoms familiar from quantum textbooks. Rather, they are so-called guiding-center atoms, in which the positrons slowly drift around the antiprotons while rapidly circling with small Larmor radii, as shown in figure 3. Collisions also look much different: When a guiding-center atom collides with a free positron, the free positron and the bound positron tend to switch places. As a result of such radically altered dynamics, the overall three-body collision rate may be about an order of magnitude slower than the field-free rate. 14 The ATRAP field-ionization results showed that the antihydrogen atoms were traveling faster than expected and that the number of atoms ionized scaled with the ionizing field in an unanticipated way. Further theoretical work revealed the complexity of atom formation in high fields. Monte Carlo simulations showed that a significant charge-exchange process was occurring and the guiding-center atom approach was starting to break down, with the electron orbits becoming chaotic for more tightly bound atoms. 15
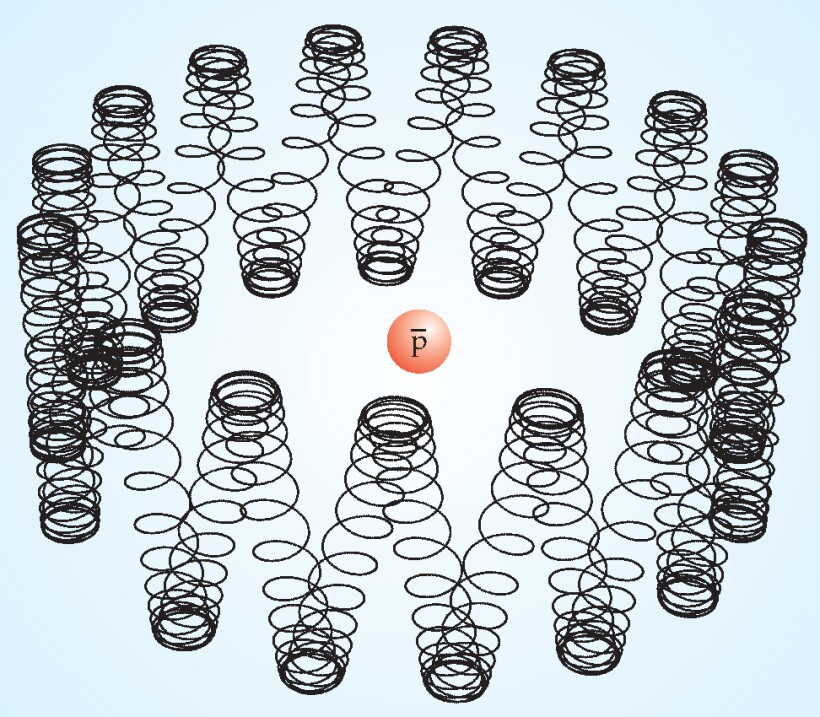
Figure 3. A classical trajectory of a positron in an antihydrogen Rydberg atom in a strong magnetic field. The positron undergoes cyclotron motion with small Larmor radius, bounces back and forth along a field line, and drifts around the antiproton. The complicated motion alters the dynamics of an antimatter plasma containing such atoms.
One can wonder whether it would make more sense to study the recombination physics of magnetized plasmas using matter—protons and electrons—rather than the much more expensive antimatter. Although hard to come by, antimatter does have certain advantages, such as easy detection through the annihilation products. Although no one has yet made a proton—electron ultracold plasma, Georg Raithel and colleagues have produced a rubidium ultracold plasma in nested Penning traps at high magnetic field. Their system may provide a recombination testing ground that can be of use to the antihydrogen community.
Future directions
As the relatively young field of ultracold plasmas continues to grow, work continues on many fronts. Ultracold plasmas are a good system for studying heat transport and global thermal equilibration in strongly coupled plasmas. Recent experiments with molecular plasmas demonstrate new phenomena such as dissociative recombination and suggest that thermalization of ions with the cold background gas in the supersonic expansion could yield larger values of the coupling constant Г. Ultracold plasmas are also being investigated as a bright electron or ion source for applications such as ion milling, microscopy, and seeding free-electron lasers. 16 Although ultracold plasmas are in many ways extremely simple systems, they display a broad range of phenomena of interest to many sectors of physics. Researchers have learned a tremendous amount by studying classical plasma concepts and by probing the effects of correlations and strong coupling. As experiment and theory explore this new playground at the boundary of plasma physics, many more discoveries will surely come.

Figure 2. Equilibration dynamics in an ultracold plasma. In the first 0.5 µs after ionization, the plasma experiences rapid disorder-induced heating as the ions’ excess potential energy is converted into kinetic energy. Thereafter, the kinetic energy exhibits damped oscillations about its equilibrium value as the cloud of ions settles into its potential-energy minimum and adopts a liquidlike short-range order, as shown in the inset.
We acknowledge Anthony Chan and Daniel Vrinceanu for helpful discussions. We acknowledge Georg Raithel for conceptual input regarding figure
References
1. S. Kulin et al., Phys. Rev. Lett. 85, 318 (2000). https://doi.org/10.1103/PhysRevLett.85.318
2. D. Bohm E. P. Gross, Phys. Rev. 75, 1851 (1949). https://doi.org/10.1103/PhysRev.75.1851
3. D. Comparat et al., Mon. Not. R. Astron. Soc. 361, 1227 (2005). https://doi.org/10.1111/j.1365-2966.2005.09245.x
4. S. Mazevet, L. A. Collins, J. D. Kress, Phys. Rev. Lett. 88, 055001 (2002); https://doi.org/10.1103/PhysRevLett.88.055001
D. Vrinceanu, G. S. Balaraman, L. A. Collins, J. Phys. A 41, 425501 (2008). https://doi.org/10.1088/1751-8113/41/42/4255015. S. G. Kuzmin T. M. O’Neil, Phys. Rev. Lett. 88, 065003 (2002). https://doi.org/10.1103/PhysRevLett.88.065003
6. T. C. Killian et al., Phys. Rep. 449, 77 (2007). https://doi.org/10.1016/j.physrep.2007.04.007
7. L. D. Landau, JETP 7, 203 (1937)
;
L. Spitzer, Physics of Fully Ionized Gases, Interscience, New York (1956).8. S. Ichimaru, Rev. Mod. Phys. 54, 1017 (1982). https://doi.org/10.1103/RevModPhys.54.1017
9. F. Robicheaux J. D. Hanson, Phys. Rev. Lett. 88, 055002 (2002). https://doi.org/10.1103/PhysRevLett.88.055002
10. N. N. Bogoliubov, in Studies in Statistical Mechanics, vol. 1, E. K. Gora, trans. J. de Boer, G. E. Uhlenbeck, eds., North-Holland, Amsterdam (1962), p. 1.
11. G. E. Morfill A. V. Ivlev, Rev. Mod. Phys. 81, 1353 (2009). https://doi.org/10.1103/RevModPhys.81.1353
12. J. P. Morrison et al., Phys. Rev. Lett. 101, 205005 (2008). https://doi.org/10.1103/PhysRevLett.101.205005
13. G. Gabrielse et al., Phys. Lett. A 129, 38 (1988). https://doi.org/10.1016/0375-9601(88)90470-7
14. M. E. Glinsky T. M. O’Neil, Phys. Fluids B 3, 1279 (1991). https://doi.org/10.1063/1.859820
15. T. Pohl, H. R. Sadeghpour, G. Gabrielse, Phys. Rev. Lett. 97, 143401 (2006). https://doi.org/10.1103/PhysRevLett.97.143401
16. M. P. Reijnders et al., Phys. Rev. Lett. 102, 034802 (2009). https://doi.org/10.1103/PhysRevLett.102.034802
More about the Authors
Thomas Killian is an associate professor in the department of physics and astronomy at Rice University in Houston, Texas.
Steve Rolston is a professor of physics and a codirector of the Joint Quantum Institute at the University of Maryland, College Park.
Thomas C. Killian. 1 Department of physics and astronomy at Rice University in Houston, Texas, US .
Steven L. Rolston. 2 Joint Quantum Institute at the University of Maryland, College Park, US .




