The stormy fluid dynamics of the living cell

Cell biology has its beginnings in the first observations of cells through primitive microscopes and in the formulation of cell theory, which postulates that cells are the fundamental building blocks of life. Light microscopes showed that the insides of cells contained complex structures, such as nuclei, spindles, and chromosomes. The advent of electron microscopy in the mid 20th century brought the first truly detailed views of cell innards. Images revealed complexity at all observable scales, including cell-spanning networks of polymers, intricate organelles made of membranes, and a variety of micron- to nanometer-sized sacs and granules such as vesicles, lipid droplets, and ribosomes. (For a glossary of cellular components, see the Quick Study by Ned Wingreen, Physics Today, September 2006, page 80 .) Those structures are immersed in or part of the aqueous cytoplasm—the cell’s fluidic medium.

Scientists have known for centuries that some plant and amoeboid cells have cytoplasmic flow inside them, as illustrated in figure 1a. Modern light microscopy has shown that such directed motions in cells are quite common. Researchers have studied those flows using such sophisticated methods as particle imaging velocimetry and simulations (see figures 1b and 1c). Such flows underlie the most basic biological functions of cells and can be a cause, an effect, or both. In any case, understanding them requires the study of forces and stresses that are created from activity inside the cell itself.

Figure 1.

The self-contained character of subcellular fluid mechanics makes its nature fundamentally different from other areas of fluid dynamics—weather, for example. Both systems are incredibly complex, but weather is driven externally, by daily and yearly cycles of rotation and orbit, whereas cells are driven internally. What’s more, the basic fluid-dynamical equations and thermodynamics of the atmosphere are known. That information enables one to predict its short-term behavior. By contrast, although our basic understanding of the molecular constituents that make up cellular structures is firm, biophysicists don’t yet have a sophisticated enough theoretical understanding to fully comprehend and predict a cell’s dynamics. Nonetheless, as with weather, we believe that fluid mechanics and flows will be an important part of the story.

Crowded and complicated

The cytoplasm is not a simple liquid. As shown in figure 2a, even a cellular volume of a few cubic microns is filled with an aqueous slurry of components: working proteins, polymer meshes, and organelles of different sizes and compositions. ¹ The slurry is active—that is, its component parts convert a local source of (usually chemical) energy to change their shape and generate forces. And the slurry can change markedly over the life of the cell. For example, organelles such as the endoplasmic reticulum—essentially tubes in the cytoplasm—fragment during cell division but otherwise form an interpenetrating structure.

Figure 2.

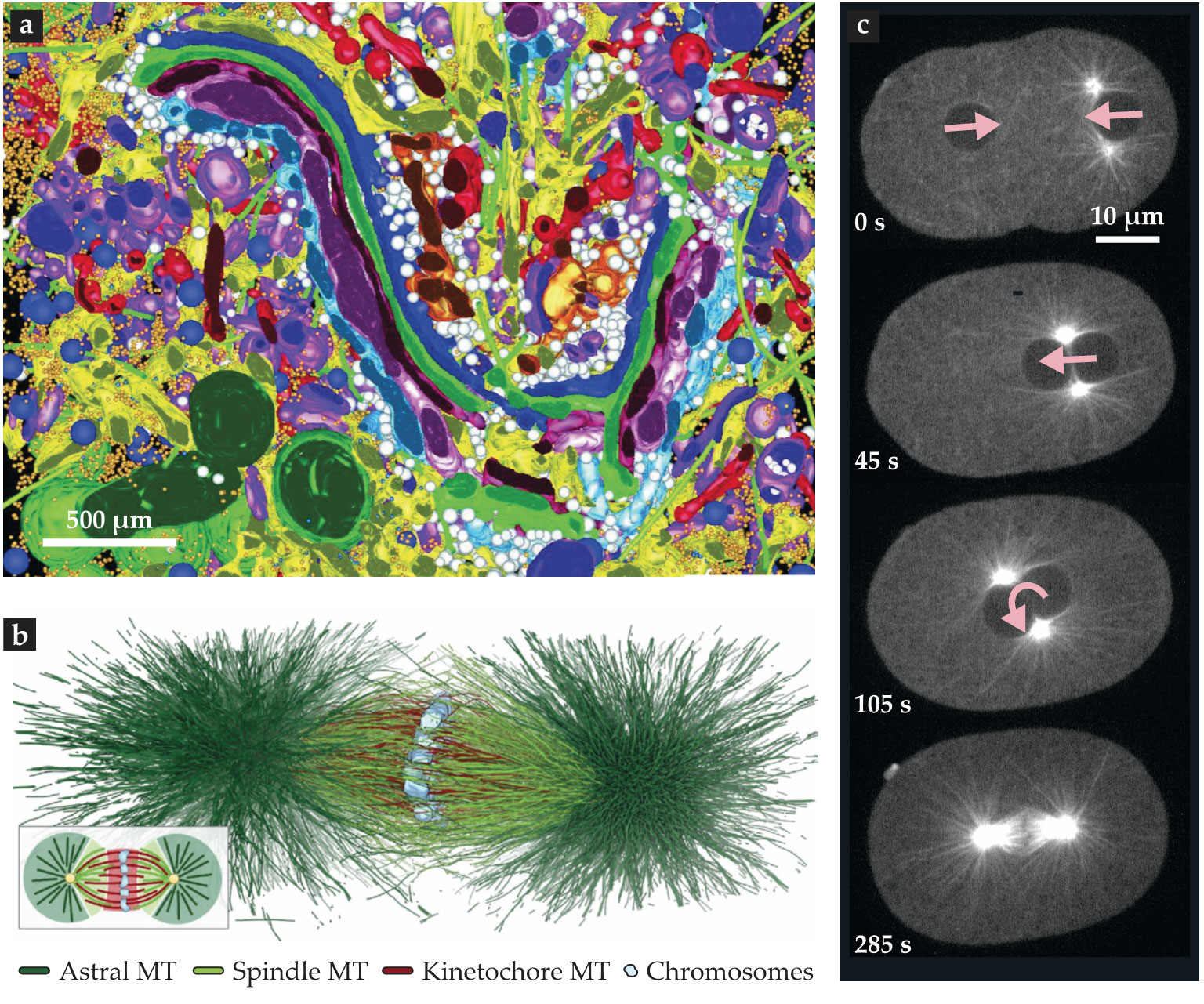
Actin and microtubule polymers are another example of active cellular components. Both are stiff filaments that constantly assemble and disassemble, with lifetimes on the order of seconds or minutes. Individually, they are transitory, but collectively, they self-organize into much longer-lived subcellular structures. Microtubules organize themselves into the spindle that segregates chromosomes during cell division, and actin organizes itself into a specialized layer of proteins known as the cortex, which has different functions, such as controlling cell shape, in different cells. Figure 2b shows an electron-tomography reconstruction of a mitotic spindle of a nematode embryo, Caenorhabditis elegans. Just 10 µm long, the spindle is a dense network of 10 000 microtubules that holds the chromosomes at its center and reaches throughout the cytoplasm.

From one viewpoint, the cell is the ultimate multiscale system, with scores of interlocking components. From another, its subcellular structures, such as the nucleus, spindle, and endoplasmic reticulum, are active materials that can be conceptualized at a coarse-grained level. Indeed, the perspective for best viewing the cell and its contents depends on the problem at hand.

An interest of ours is how, after fertilization, DNA from mother and father come together and become positioned in the middle of the cell. Figure 2c shows snapshots of that process. At its start (t = 0 s) the DNA is located inside membrane-bound organelles called pronuclei, with arrays of stiff microtubules attached to the male pronucleus. Those structures come together to form the pronuclear complex (t = 45 s), which migrates through the cytoplasm to the cell’s center, where it rotates to align with the cell’s long axis (t = 105 s). There, the pronuclear membrane breaks down and the mitotic spindle forms (t = 285 s, roughly corresponding to figure 2b). To understand pronuclear migration, it’s useful to think of the cytoplasm as a viscoelastic continuum.

Accounting for forces

Living cells are small, and their internal motions are slow. That truism simplifies the fluid dynamics. Consider a body of linear dimension l moving with speed u in a cell whose cytoplasm has a viscosity µ and density ρ. The cytoplasm’s Reynolds number, the ratio of inertial to viscous forces, is given by (1) $$\mathit{Re}=\frac{\mathrm{inertial\; force}~\rho u^2{l}^2}{\mathrm{viscous\; force}~\mu ul}=\frac{\rho ul}{\mu }$$ Take the transport of an l ≈ 10 µm pronucleus in C. elegans as a paradigmatic example. The cell’s cytoplasm has a viscosity about 1000 times that of water, and the embryo’s pronucleus moves through it with speed u ≈ 0.1 µm/s. That yields a Reynolds number of approximately 10⁻⁹, a situation in which inertial forces are so low they’re irrelevant.

Such a low Reynolds number puts us in the regime famously discussed by Edward Purcell ² in his paper “Life at low Reynolds number,” in which the velocities of objects follow from balancing applied forces with viscous drag. Whereas Purcell’s article explored small things living and moving in fluids, here we explore fluids moving in small things.

One can think of the cell’s interior, crowded with various organelles and polymer networks, as an active, multiphase material that is both viscous and elastic. ³ For viscoelastic materials a common measure of the relative importance of viscous to elastic responses is the Weissenberg number, (2) $$\mathit{Wi}=\stackrel{·}{\gamma }{\tau }_{\mathrm{e}}$$ where $\stackrel{·}{\gamma }$ is a typical strain rate of the flow and ${\tau }_{\mathrm{e}}$ is the relaxation time of the elastic medium. The migration of the C. elegans pronuclei to the center of the cell is slow and happens over the time scale of minutes. So, we estimate $\stackrel{·}{\gamma }$ ~ u/l ~ 10⁻² s⁻¹. The faint elastic response ⁴ of the embryonic cytoplasm produces a relaxation time ${\tau }_{\mathrm{e}}$ ~ 1 s. Thus, Wi = 10⁻² ≪ 1, and for the purposes of studying positioning, the cytoplasm can reasonably be treated as a purely viscous medium.

That approximation considerably simplifies the response of the cytoplasm to motion, but it’s not universal. Some events, such as ruptures of the nuclear membrane, can be more rapid; in cancer cells they happen on time scales of seconds. Such fast motions yield much higher values of Wi. In general, a cell’s internal mechanics are cell-type and cell-stage dependent, and its mechanical responses are a function of both the length and time scales of the measurement ¹ and of where in the cell the responses are measured. ⁴

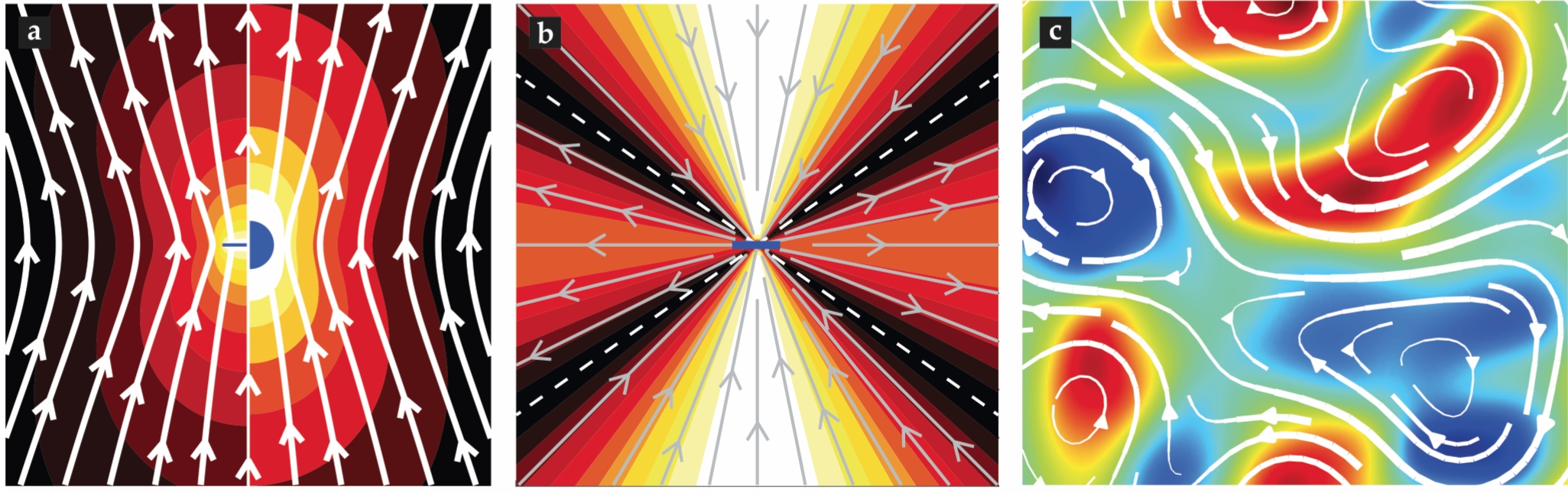
Viscous forces alone lead to unusual features of cell mechanics. One is the nature of drag on moving objects: At low Reynolds number, drag scales with length as μlu. Consider a microtubule having the same linear dimension as the pronuclear payload, l = 10 µm, and moving at the same speed. That microtubule is just 25 nm in diameter, which makes its surface area 1/1000 that of the pronucleus, yet it’s drag is nonetheless 1/4 of the pronucleus drag. That’s because drag in that regime results from objects shearing the viscous fluid; even thin objects carry along and distort large regions of fluid (compare the left and right sides of figure 3a). Our daily experience, by contrast, takes place mostly in high-Reynolds-number environments, where just by moving we push fluid aside with the surface area we present to it.

Figure 3.

That microtubules carry considerable fluid is underappreciated. Scientists unfamiliar with fluid mechanics tend to think of the cytoplasm as simply a source of local friction on objects moving through it. That assumption can lead to the wrong conclusion that drag is an additive force. It would imply, for instance, that the drag on a 10 000-microtubule array—roughly the number in the C. elegans pronuclear complex—would be 10 000 times the drag on a single microtubule. It turns out, though, that comoving microtubules in an array collectively entrain fluid, or equivalently, move in each others’ wake. Thus, drag on the assembly is on the order of the drag on just a single microtubule.

When microtubules or other objects carry fluid around, confinement by cell boundaries can have a surprisingly strong effect. To appreciate the consequences, imagine the single-cell C. elegans embryo as a sphere of diameter L ≈ 50 µm filled with purely viscous cytoplasm, and the pronucleus as a sphere of diameter l ≈ 10 µm. A classical solved problem in a low-Reynolds-number flow is the drag on one sphere moving in a larger sphere. It depends fundamentally on only the geometric ratio—the so-called confinement number Cn, the ratio of the payload size to the confining dimension: (3) $$\mathit{Cn}=\frac{l}{L}$$ For Cn = 0.2 it takes almost twice the force to move the payload at a given speed as to move it in an unbounded medium. The required force increases quickly with Cn and is the cost of redirecting the induced cytoplasmic flow at the cell periphery. Further accounting for the presence of attached microtubule arrays, which effectively increases l and hence Cn, results in a 100-fold increase in drag. ⁵

Internal forces drive internal flows

Motions, and hence flows, in cells are often driven by motor proteins that move in the cytoplasm. Many of those motor proteins can sequentially bind to, move along, and unbind from polymers, such as microtubules and actin. That generates forces between the motor and polymer, and the resulting directed motion is only possible because motor proteins transduce chemical energy supplied by adenosine triphosphate (ATP), which is held out of equilibrium with its breakdown products by the cell’s metabolism. Energy available from the disequilibrium of ATP and its breakdown products acts as a battery that motor proteins can tap to perform mechanical work. When abutting or attached to other objects, the polymers themselves can also generate active forces through their assembly or disassembly.

For cellular forces, intuition can be highly misleading. For example, the magnitude of a conservative force such as gravity or electrostatics on an object can be measured by determining the experimentally applied opposing force that halts the object’s motion. But that procedure fails utterly in the case of motor proteins. To understand why, keep in mind that the force between a polymer and an isolated motor is balanced by drag through the surrounding fluid.

Because of the motor’s small size (about 1 nm) and speed (about 1 µm/min), that drag is about 1 femtonewton. Applying an opposing force to the motor slows it down, but a motor protein typically halts only when it is subject to forces in the piconewton range, thousands of times greater than the forces it exerts in the absence of additional applied forces. The upshot is that forces exerted by motor proteins in situ cannot be measured simply by subjecting the proteins to external forces.

Inside cells, motor proteins exert forces in different ways, and those forces have consequences for the flows they produce. For example, the mechanism of pronuclear migration is currently debated: Some researchers argue that the pronuclear complex is positioned by motors anchored at the cortex; others argue that it’s positioned by motors in the cytoplasm. The first model postulates that motors fixed on the cell boundary reel in the microtubules they walk on. Microtubules would thus be transported to the cell surface and drag along the pronuclear complex and the neighboring fluid.

In the second model, by contrast, motors in the cytoplasm bind and walk along microtubules and thereby induce fluid to flow along the microtubules’ surfaces. By momentum balance, pushing fluid backward propels the microtubule forward so that it “swims” through the cytoplasm. Measurements of fluid flow should provide a clear way to determine which model is correct: Roughly speaking, motors at the cortex would drive fluid in the same direction as the pronuclei, whereas motors in the cytoplasm would drive fluid in the opposite direction. But the detailed predicted flow patterns are complicated by the incompressibility of the fluid and confinement from the cell boundary. ⁵

The movement of motor proteins on polymers in the cytoplasm is ubiquitous in cell biology. The resultant forces between the motors and polymers must be equal and opposite. Thus, the forces those objects exert form force dipoles (see figure 3b). Collections of objects exerting dipolar forces on fluids can produce spectacular phenomena, such as self-organized, swirling flows called active turbulence, shown in figure 3c, and confinement-induced coherent flows. Both types have been observed in cell extracts and reconstituted mixtures of motor proteins and microtubules. ⁶

That purified biological components can robustly create such intricate patterns of flow is remarkable. In vitro systems may chart a promising pathway to investigate principles relevant for subcellular biological fluid mechanics and self-organization. And they open the possibility of engineering artificial, active materials with lifelike properties. The dynamics of such collections of objects exerting dipolar forces on fluids can be characterized in terms of the activity number (4) $$A=\frac{\mathrm{active\; forces}~\sigma c}{\mathrm{viscous\; forces}~\frac{u}{L}\mu }=\frac{\sigma cl}{u\mu }$$ Here c and σ are the concentration and magnitude of force dipoles, respectively; u is the characteristic fluid velocity produced by a dipole, and L is the system size. When A exceeds a critical value, the system changes to a state of active turbulence. ⁷

When polymers are anchored to the cell boundary, as for the actin cortex, motors can move along the boundary. The force acting on the motor from the boundary is balanced by the drag force generated by the motor moving through, and shearing, the fluid that surrounds it. When such motors are at low density, they move relatively independently of each other. At high density, the parcels of fluid dragged by the motors overlap, which can lead to large-scale flows in the cytoplasm.

At what density of motors does the large-scale flow occur? Objects in a fluid create flow perturbations on the scale of their own size, so for the fluid to be entrained collectively, the spacing between motors must be comparable to their size. Motor proteins are a few nanometers in size but typically microns apart in cells. With that spacing, motors are unlikely to produce coherent flows—that is, to carry the fluid collectively. But in many contexts motor proteins transport not just themselves, but also micron-sized organelles. The additional fluid moved by the large payloads can be sufficient to produce bulk flows in cytoplasm. Known as cytoplasmic streaming, such bulk flows are observed in a wide variety of systems, including plant cells and egg cells. ⁸

Diffusion helps and is hindered

The flows generated by cytoplasmic streaming or active turbulence can, in principle, advect and mix objects in the cytoplasm. In addition to being carried by the flows, mobile objects can also collide randomly with neighboring molecules and give rise to diffusive motion. The size of cells and the mobile objects in them greatly influences the efficacy of transport processes. ¹ The Peclet number (5) $$\mathit{Pe}=\frac{ul}{D}$$ quantifies the relative importance of the rates of advection and diffusion for an object moving at a velocity u over a length l, where D is the diffusion coefficient. The dependence of Pe on the length scale over which transport occurs shows that advection becomes increasingly important as length scales get larger. The size dependence may explain why cytoplasmic streaming is most commonly seen in large plant and algal cells, but it doesn’t solve the problem of how cellular reactants become well mixed. That process might require complex flows that stretch fluid to bring reactants into close proximity or to enhance the effective diffusion through dispersion (reference ; see also the article by Michael Brenner and Howard Stone, Physics Today, May 2000, page 30 ). The flows produced by active turbulence are well suited for such mixing and may be useful in microfluidic devices.

Models and methods

The numerical modeling of flows in cells is still in its infancy. The cells’ internal complexity makes the task computationally demanding and reliant on fluid models to organize and account for the complexity. The most basic fluid model is the incompressible, homogeneous Stokes equations of a low-Reynolds-number flow, which is solved as a boundary-value problem using the forces and velocities of objects moving in the fluid. In other settings, the Stokes equations are replaced by simpler porous-medium approximations, or forcing terms are added to model the effects of immersed structures.

Usually, the modeling approach depends on the particular cell in question and on the goal of studying it. In the case of pronuclear positioning, microtubules are the objects through which forces are transmitted to the pronuclear complex. Simulating microtubules introduces a few challenges. For starters, microtubules are extremely thin and yet microns long. They are also numerous, typically with 10 000 in an array, which complicates the flow geometry. What’s more, motor proteins can readily bend the microtubules, which further complicates the geometry. And finally, microtubules are transitory, typically living just 30 s, and they exhibit various lengths because of their constant assembly and disassembly. That heterogeneity leads to a wide range of time scales because relaxation times from bending are length dependent.

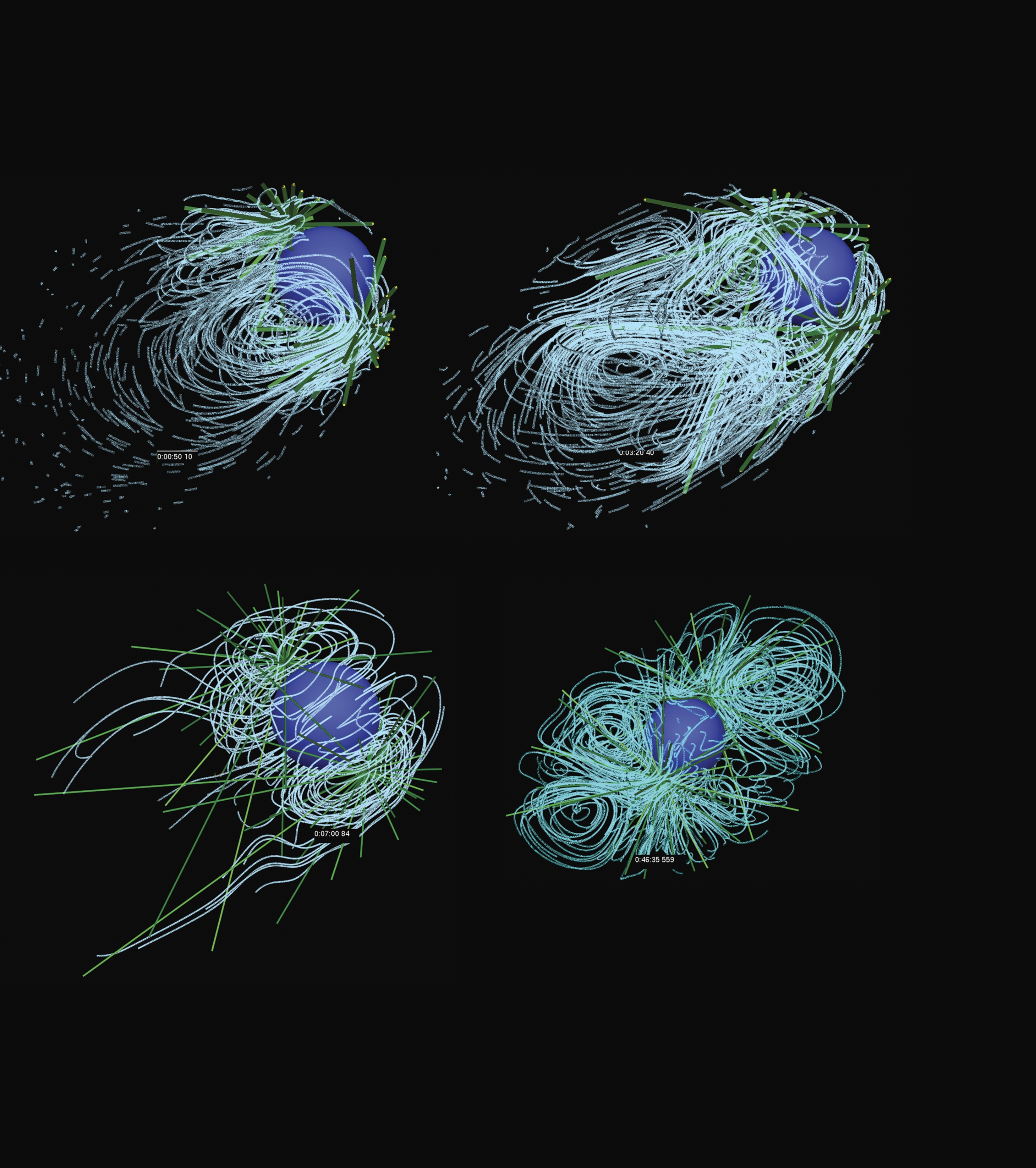
We have recently developed specialized methods to simulate the fluid dynamics of microtubule systems. The methods use Green functions of the three-dimensional homogeneous Stokes equations to derive integral equations on immersed and bounding surfaces. Because of the thinness of microtubules, the integrals over their surfaces can be further reduced to 1D line integrals. These reductions in dimensionality, together with other techniques, simplify the simulation of the flows generated by thousands of moving, bending microtubules over time scales (typically tens of minutes) that are relevant to pronuclear transport. ⁵

Those methods are optimal for capturing the detailed hydrodynamics of microtubules, but they remain limited in scope and can handle at best a few thousand filaments. In other cases, researchers are interested in hundreds of thousands or even millions of cytoskeletal filaments. Capturing the hydrodynamics of such problems requires approaches that “coarse-grain” the fine details. In the example of Drosophila oocytes, molecular motors moving on wall-anchored microtubules set up complex flows believed to move signaling molecules about the cell and help establish its internal asymmetry, or polarity. 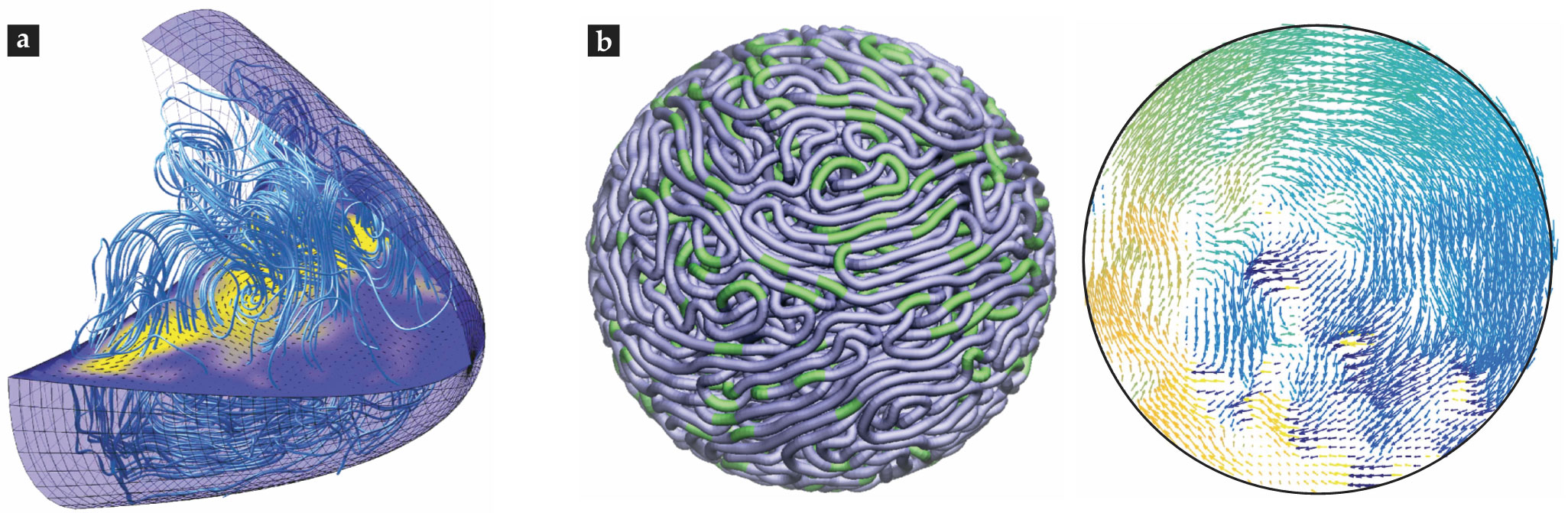⁹ Biophysicists have studied the flows produced by the motors’ activity by numerically solving a Stokes equation augmented by a coarse-grained forcing term that represents the directed motion of the motors moving along microtubules (see figure 4a).

Figure 4.

For other problems it is useful to treat the internal mechanics of the cell as arising from a coarse-grained, possibly multiphase, complex material. In that general approach the cytoplasm is modeled as particle-packed, or visco(poro)elastic, and driven by internal forces from molecular motors or polymerization. ⁴ The biophysics of cell motility is one area in which considerable efforts have been made to simulate such coarse-grained models. ¹⁰ A related area is that of cell-shape changes, which arise naturally in cell motility and in cell–cell interactions.

Finally, not all cellular fluid dynamics takes place in the cytoplasmic volume. DNA can move in seemingly coordinated ways in the cell’s nucleus. Recent modeling and simulations suggest that those motions may arise from force dipoles created by molecular machines acting within the fluidic nucleoplasm, ¹¹ as shown in figure 4b.

A to-do list

For understanding subcellular fluid mechanics, this article has outlined five dimensionless numbers: the Reynolds, Weissenberg, confinement, activity, and Peclet. It is easy to think of others, such as the volume fractions of mobile particles and of polymer meshes and arrays. As the study of subcellular fluid mechanics matures, the dimensionless numbers postulated to describe it will grow, no doubt, to rival the variety commonly used to categorize the dynamics of Earth’s oceans and atmosphere.

Much work remains. Biophysicists still lack validated theories of the collective properties of active fluidic materials and a framework that explains how large-scale behaviors, such as active turbulence, depend on the behaviors of constituent molecules. The contribution of fluid mechanics to distinct subcellular phenomena is also yet to be worked out. And its absence is a major hurdle to understanding the mechanics and behaviors of those phenomena.

Progress will surely require new conceptual and technical advances. The potential payoff for such work is huge. Not only will it provide insight into beautiful and mysterious processes that epitomize the unique properties of living matter, it will also have practical import. Just as an understanding of planetary fluid flows (see the article by Erdal Yiğit and Alexander S. Medvedev, Physics Today, June 2019, page 40 ) has enabled predictions of the weather and led to transformative economic and social improvements, an understanding of cellular fluid flows will allow scientists to predict the behavior of biological processes. And those predictions, in turn, are likely to have a transformative effect on the treatment of diseases.