The physics of eukaryotic chemotaxis
DOI: 10.1063/PT.3.1884
A small scratch on the skin can be quite painful. Fortunately, the pain is transitory and dissipates quickly once the wound heals. The healing process is facilitated by neutrophils, a type of white blood cell that removes bacteria and other foreign materials from a wound. Neutrophils normally reside in your circulatory system but, when needed, are able to leave the bloodstream and efficiently navigate through connective tissue to the injured area. How do they figure out where to go? The answer is chemotaxis, the process of cells following chemical gradients.
In addition to wound healing, chemotaxis is important to many other biological processes. Chemical information can help sperm find the egg cell during fertilization. In embryonic development, cells are often directed to their proper location through gradients. Chemotaxis can also aid the spread of cancer during metastasis, the process by which cells leave the primary tumor and seed new tumors in other parts of the body. Experiments have shown that gradients of growth factors guide an initial step in the metastatic process; that step involves the movement of malignant cells away from the tumor and toward blood vessels.
A model amoeboid
The above examples involve eukaryotic cells—nucleus-containing cells that form the basis of multicellular life. Chemotaxis, however, is not limited to eukaryotic cells but is also employed by bacterial (prokaryotic) cells. Bacteria typically use chemical gradients to determine the location of food sources. The motility mechanisms they employ, however, are fundamentally different from the ones used by the much larger eukaryotes (see the article by Howard Berg in Physics Today, January 2000, page 24
In this article, we review the physics behind eukaryotic chemotaxis using a model system, the crawling motion of the amoeboid Dictyostelium discoideum. When they are deprived of food, Dictyostelium cells use chemotaxis to form large-scale aggregates. That survival mechanism eventually leads to a so-called fruiting body, an approximately 1-mm-tall stalk with a spherical head containing spore cells. Dictyostelium has become a favorite model system for chemotaxis among biologists and physicists alike for a number of reasons. First, its cells are relatively easy to grow and do not require special temperature or atmospheric conditions. Second, they move much faster than most chemotaxing cells, at approximately one cell diameter (10 µm) per minute. Third, the Dictyostelium genome has been fully sequenced and annotated, which makes it relatively easy to construct fluorescent markers and mutants that can be used to probe the dynamics of the molecular components involved in chemotaxis. As a result, scientists have generated high-quality quantitative data that can be used to construct accurate mathematical models. Conversely, predictions generated by modeling studies can often be tested directly in experiments. Of course, those advantages would be limited if the chemotactic mechanisms employed by Dictyostelium were unique to that species. Fortunately, the general mechanisms that underlie chemotaxis and motility are similar for many cell types, and many of the molecular components are conserved across different species.
Chemotaxis in brief
Because of the similarities, we introduce eukaryotic chemotaxis in a cell-independent way. As shown schematically in figure 1, a cell can detect external chemical signals through receptors that are embedded in the cell membrane and that reversibly bind the externally diffusing chemicals. Those receptors are distributed uniformly along the cell body; a priori, there is no cell front or back. If the cell is placed in a gradient, the resulting distribution of bound receptors becomes asymmetric, with more bound receptors in the membrane at the locations where concentrations are highest. Subsequent conformational changes of the receptors lead to the excitation of internal signaling pathways. Some of the pathway components become localized or are activated at the front or the back of the cells. That polarization leads to a breaking of the cell’s internal symmetry, 1 as seen in figure 2, which shows the response of cells to a chemoattractant gradient created by a leaking pipette. The cells have been engineered to contain a green fluorescent protein that binds to one of the signaling components of the internal pathway. All cells display a fluorescent crescent at the membrane closest to the pipette, indicating an asymmetric distribution of that signaling component. Importantly, that asymmetry is not permanent; it can be changed by repositioning of the pipette.

Figure 2. Sensing and signaling a gradient. In these Dictyostelium discoideum cells, green fluorescing regions indicate the response of a signaling component to a chemoattractant gradient produced by a pipette shown at the center of the image (red region). The front–back asymmetry in the distribution of the signaling component is several times greater than that of the chemoattractant concentration—that is, the chemical input signal has been significantly amplified. To decouple signaling from motion, the cells were treated with latrunculin, a drug that renders the cells immobile and round. (Image courtesy of Christopher Janetopoulos, Vanderbilt University; see also ref.
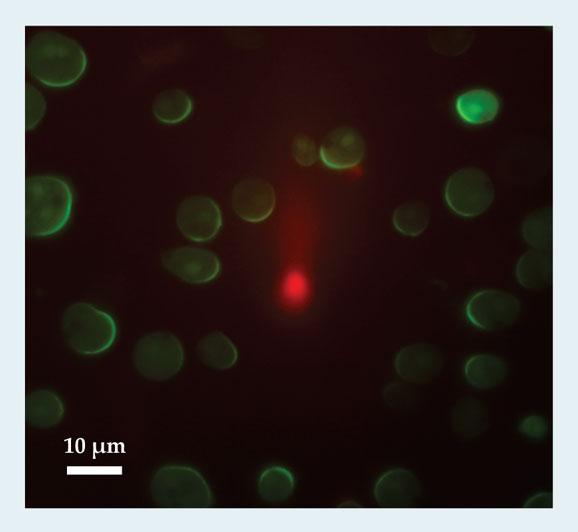

Figure 1. Chemotaxis in a nutshell. This illustration shows a cell moving to the right in response to a chemical gradient indicated by the gray-scaled background. The white lines show the outline of the cell membrane at earlier times. The motion-inducing gradient is detected by the cell through the binding of chemoattractants, shown as green balls in the inset, to receptors bound to the cell membrane. Changes in the shape of the receptors trigger internal signaling pathways; some pathway components are localized at the front of the membrane (red), others congregate at the back (green). Called pseudopods, membrane protrusions (orange) self-organize at the front of the cell. The inset also shows the branched actin network (light blue) that pushes the membrane forward, with several individual filaments highlighted in red.
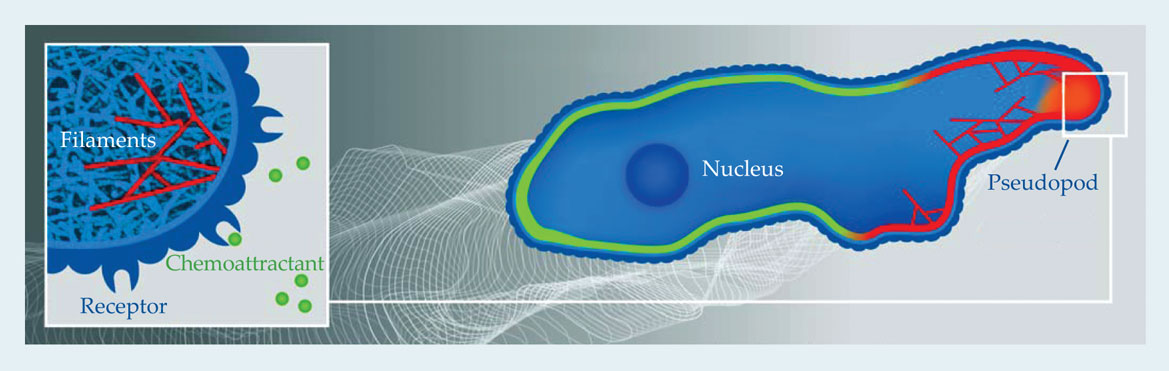
In time the cascade of internal signaling events results in the polymerization of actin filaments at the front of the cell. 2 The filaments push against the membrane and deform it. In Dictyostelium, the deformations result in localized regions of protrusion called pseudopods. Obviously, for net translation, protrusive movement at the front needs to be complemented by retraction at the back. That retraction is partially mediated by the motor protein myosin, which is also responsible for our own muscular contractions. The protrusion and retraction forces act on the cell and its membrane, a lipid bilayer whose shape is affected by such physical properties as surface tension and bending rigidity. Forces generated by actin polymerization and myosin contraction combine with friction with the cell’s surroundings to determine all mechanical aspects of cell motion.
Physics is involved in almost every level of the chemotactic process. The binding and unbinding of molecules to the receptors is an inherently stochastic process, and several interesting sensitivity questions can be addressed with techniques developed in statistical physics. Understanding the subsequent recognition of the gradient by the internal pathways and the concomitant polarization of the cell requires the development and analysis of spatially extended nonlinear reaction–diffusion models. The physics of elasticity is critical for determining how the internally generated forces create motion. Moreover, physics can be useful in the development of novel experimental techniques. Microfluidic devices that precisely control the conditions experienced by cells have become an integral component of chemotactic experiments. In the following sections, we look more carefully at some of the crucial physical processes underlying cell motility.
Signal detection
The first requirement for directed motility is the detection of an external gradient. Experiments show that a Dictyostelium cell can discern a change in chemical concentrations across its body of only a few percent; moreover, that exquisite sensitivity persists for a large range of background concentrations. 3 As already mentioned, cells sense chemical gradients via specialized proteins embedded in their membranes. Those surface receptors reversibly bind the chemical to be detected and report the results to the cell interior through changes in the shape of their cytoplasmic segments. For Dictyostelium, the protein responsible for chemotaxis is cAR1 (cyclic AMP receptor, type 1), a prototypical G-protein-coupled receptor of the type used throughout the biological world to detect external environmental conditions.
A Dictyostelium cell has about 70 000 cAR1 proteins, each of which acts as an independent two-state system, either bound (denoted by S = 1) or unbound (S = 0) to the chemical to be detected. The rate of binding of a receptor is proportional, with coefficient k+, to the chemical concentration c at its location. On the other hand, the rate of unbinding (k−) is constant. Thus in equilibrium, the probability of occupation of a single receptor is

where Kd = k−/k+ is the dissociation constant, the concentration at which the occupation probability equals 0.5. For the entire array of N receptors, neglecting for the moment any motion they might have, the overall distribution is just the product of independent binomials given by equation
The receptor distribution conveys information about the gradient’s direction. To see how, imagine a two-dimensional circular cell of diameter d with receptors located at equidistant angles θj and consider the cell placed in a linearly varying field. The statistic Φ defined through

acts as an estimator of the gradient direction. (“Arg” stands for “argument,” the phase of the complex number that follows the term.) That is because, in the sum on the right-hand side of equation
To compute the signal-to-noise ratio (SNR) for the estimator Φ, we will focus for simplicity on small gradients. Then the strength of the directional signal is directly proportional to the cell diameter d multiplied by the magnitude of the gradient of the occupation probability, ∣∇[c/(c + Kd)] ∣. The noise is due to the inherent fluctuations of the sum in the definition of Φ. To lowest order, one may neglect the gradient in calculating the variance of Φ; the result, up to a geometrical factor, is

with c‾ the mean concentration. Dividing the strength of the signal by the square root of the variance gives for the signal-to-noise ratio

With tools borrowed from information theory, one can derive more general expressions valid for finite gradients, more complex cell shapes, and nonuniform receptor spacing.
In deriving equation
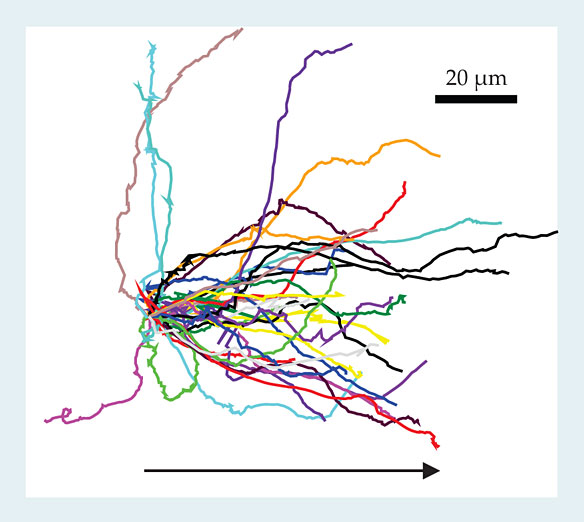
Recently it has become possible to compare the above detection theory with results of experiments that exploit microfluidic technology. The microfluidic devices can easily be designed and manufactured to allow for precise control of the chemical concentrations presented to cells. With that technology, a researcher can obtain reproducible distributions of cell behavior as a function of applied conditions; figure 3 shows an example. Careful quantitative measurements via such devices have confirmed the intuitive notion that at small SNR, cell behavior is limited by the cell’s ability to accurately detect gradient directionality. 4

Figure 3. Cell tracks. The colored lines, whose origins have been brought to a common point, depict the observed paths of Dictyostelium discoideum cells through a chemical solution whose concentration changes by 10% across the 10-µm distance typical of a cell diameter. The tracks exhibit considerable motile variability; even for gradients steeper than those pertinent to the figure, a typical maximal chemotactic index, defined as the ratio of the distance traveled in the gradient direction to the total distance traveled, is at most about 0.7. The arrow indicates the direction of increasing chemoattractant concentration. (Adapted from ref.
Of course, not all sources of noise are directly due to the stochastic binding–unbinding process. For example, the cell is moving and changing shape as it does, and the receptors themselves can diffuse in the membrane, at least over short distances. However, given the typical one-second time scale for detection, effects due to motion are rather small. Suppose, for example, that a cell moves at a speed of 0.1 µm/s through a solution with c = Kd = 50 nanomoles/liter ≡ 50 nM and a concentration gradient of 1 nM/µm. Then the change in occupation probability after one second is roughly 10−3. In contrast, the standard deviation of the binomial binding–unbinding process is √
In addition, the chemoattractant ligand concentration itself fluctuates, as studied in the seminal work of Howard Berg and Edward Purcell on chemosensing in bacteria 5 and as extended by others. 6 Those fluctuations eventually increase the amount of time it takes to equilibrate the receptor array to a changed chemical field. 7
Signal processing
After detection comes processing. Chemical networks in the cell interior sense the difference in receptor occupation probability, use that information to “decide” on the gradient direction, and polarize the cell accordingly. Such chemical networks and their role in cellular information processing have become popular research topics of late, and they have been studied extensively with techniques borrowed from the physics of nonlinear dynamical systems. One application is to stem cells, which retain maximal flexibility in their functional capabilities and can become more specialized in response to external signals.
The chemotaxis network is more complex than the stem cell’s circuit, which responds only to average chemical concentrations. A gradient response arises via a comparison of receptor binding values from different parts of the cell, a process that requires communication of information between different cell parts to ensure that only the cell part experiencing the highest local concentration will be identified as the front. That communication could be chemical, mechanical, or both.
A simple assumption proposed by Carole Parent and Peter Devreotes is that the communication takes the form of a diffusing messenger that inhibits signals leading to the actin polymerization responsible for protrusions. 8 That assumption has been incorporated into numerous modeling studies, and although the details differ from model to model, the basic idea is that the cell’s response is governed by a competition between that global signal and a locally produced, membrane-bound activator.
The 2D LEGI (local excitation, global inhibition) equations introduced by Andre Levchenko and Pablo Iglesias offer a specific realization of how that competition might work. 9 In their model, an input variable S(s), which depends on position s along the membrane and reflects the likelihood that a receptor at s is bound, directs the production of a membrane-resident activator with concentration A and an intracellular inhibitor with concentration I. The activator and inhibitor, in turn, have competing effects on a downstream, surface-bound response element with concentration R. Specifically,

where D is a diffusion coefficient. Equation

The key mechanism embodied in the above model can be seen by considering a uniform signal S. Equations
To test that basic property, one needs to identify specific molecules related to the abstract activator, inhibitor, and response variables in the LEGI equations. Earlier we introduced cAR1 as a G-protein-coupled receptor. The nomenclature refers to the first stages of the intracellular processing cascade, which involves the dissociation of a specific protein—a G protein—into separate parts that can catalyze downstream effects. One result is the activation of the Ras protein 10 via the exchange of a low-energy nucleotide (guanosine diphosphate, or GDP) with a high-energy one (guanosine triphosphate, or GTP). The exchange is catalyzed by a guanosine exchange factor (a RasGEF) and the reverse process by a GTPase-activating protein (a RasGAP). The simplest possibility is to associate the activator with the RasGEF, the inhibitor with the RasGAP, and the response with the concentration of activated Ras.
Armed with that dictionary, we joined other colleagues to quantify the activated Ras response of Dictyostelium cells to abrupt changes in chemoattractant concentration and found that the response did indeed perfectly adapt after roughly 30 seconds.
11
Furthermore, we were able to argue that of all possible means of achieving perfect adaptation, only the incoherent feedforward topology at the heart of the LEGI model and described in the
In the simple LEGI model we have been discussing, the ratio of the response between the front and the back of the Dictyostelium cell is no greater than the ratio of the concentration of the external chemoattractant. But Dictyostelium cells can detect very shallow gradients, which suggests that one key early step of the processing machinery is the amplification of the external gradient. Indeed, experiments using fluorescent markers have revealed greater than fivefold amplification. 12 , 13
Differing models of chemotaxis incorporate that amplification in a variety of ways. One speculative idea that shows promise
14
involves replacing the second part of equation

The equilibrium value of R can be strongly amplified if the constants KI and KA are small, and if β ≡ krAeq/k−rIeq ≈ 1. That is, in the specified parameter regime, even a small change in the ratio of A to I will dramatically change the value of R.
Pseudopod formation
The online version of this article includes
In fact, 15 the pseudopods form at locations that correspond to the stochastic appearance and disappearance of patches of activated Ras (see figure 4a). Evidently, although the LEGI mechanism explains how the gradient limits activation to the front of the cell, the story outlined so far needs to be augmented by additional dynamical processes for it to be quantitatively applied to moving cells. In our view, the most compelling hypothesis is that the formation of pseudopods is an excitable process due to the positive feedback present in the dynamics of actin polymerization. 15 , 16

Figure 4. Pseudopod dynamics. (a) This chemotaxing cell, which is moving to the right, contains a fluorescent marker that shows when the regulator protein Ras is activated. The marker displays dynamic patches—regions of elevated fluorescence intensity that come and go—that are correlated with the formation of pseudopods at the cell’s leading edge. (b) Pseudopod formation may be an exemplar of so-called excitable processes, which amplify perturbations. The plot here represents the simulated behavior of a circular cell during an excitable process. Colors depict the value of one component in the model of reference
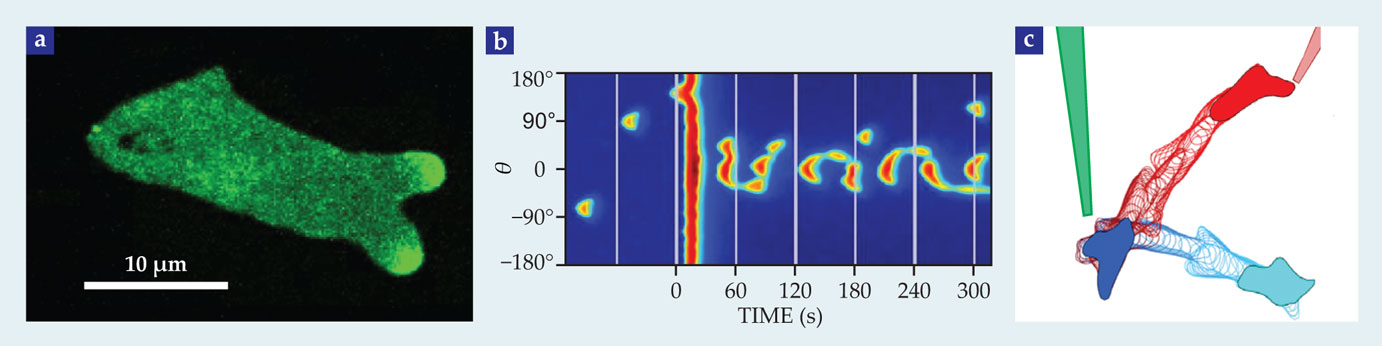
An excitable process is one by which a system will strongly amplify an above-threshold perturbation of a stable state but eventually return back to that original state. In biology, the best-known example of such a process is the propagation of electrical waves down the axons of neuronal cells due to positive feedback between voltage and conductance. Actin at the leading edge of a motile cell forms a branched network that is constantly growing via both the addition of monomers and the catalyzed formation of new branches. As the network grows, it creates free ends that further accelerate the growth—hence, positive feedback.
Several groups have built models of pseudopods by combining the LEGI paradigm with excitable dynamics (see figure 4b). Because the dynamics are excitable, a pseudopod has a finite lifetime, as is typically observed. The coming and going of individual protrusions implies that a cell will be able to quickly redirect its response following a change in the gradient direction.
How does one test some of the above ideas and couple them to actual cell motion? A fully comprehensive cell-motility model would include such physical properties of the membrane as surface tension and bending rigidity, the adhesive forces between the cell and its surroundings, and internal signaling pathways. Furthermore, experiments have demonstrated that the cytoskeleton, or cellular scaffolding, is not stationary but instead flows within the cell, so a comprehensive motility model would need to incorporate the viscoelastic dynamics of the actin network. Incorporating all those features is a major challenge for the future. In the interim, investigators have gotten insight by using simple geometrical assumptions regarding membrane dynamics to study motility models that relate protrusion forces (as determined by the excited patches) to actual cell shape and motion. Reference describes one such model that we developed with other colleagues, in which membrane motion is given by

Here, f(R) represents the driving force that is associated with patches of a response element R, vn is the normal component of the membrane velocity, κ is the curvature, γ represents the membrane rigidity, λ is a friction coefficient, and C is a Lagrange multiplier to implement the constraint that the total enclosed area remains equal to A0.
Our model produces realistic motion, an example of which is shown in figure 4c. What is more important, it can help scientists develop insight into how the different dynamical processes involved in cell motility interact. Such insights can then be tested on experimental data and on more quantitatively realistic models of cell mechanics.
In our approach, the gradient “instructs” the cell as to where to place pseudopods. As we have discussed, that notion is supported by observations of gradient sensing in immobilized cells, as seen in figure 2, and by the measurements of adaptation described in the
The combined efforts of the physicists and biologists—both theorists and experimentalists—who have studied chemotaxis have revealed a fascinating set of dynamical processes that allow the cell to go from the molecular input to the utilitarian output. The lessons we have learned may see practical applications in preventing tumor cells from navigating to the bloodstream, enhancing wound healing, and so forth, though such applications are far from certain. What is certain is that we have learned and will continue to learn valuable lessons about the myriad of ways in which physics sets up the framework inside which biological systems manage to accomplish the art of living.
Activators and inhibitors fight to a draw
Perfect adaptation occurs when a steady-state response signal R—for example, the concentration of a regulatory protein—is independent of an input signal S such as the concentration of a chemoattractant. 18 One pathway to perfect adaptation is the so-called incoherent feedforward topology. As shown schematically in the left-hand panel, it involves an input signal that leads to the production of both an activator A and an inhibitor I.

The incoherent feedforward topology lies at the core of equations
The incoherent feedforward topology is qualitatively and quantitatively consistent with experiments that have measured the response of activated Ras (a regulator protein) in Dictyostelium discoideum cells following a sudden change in the concentration of cAMP, a chemoattractant. The right panel, adapted from reference , shows the near-perfect adaptation response. The parameter I(35) denotes the fluorescent intensity of Ras 35 seconds after the application of the stimulus, normalized to the initial intensity. The concentration of cAMP is in nanomoles per liter.
Supplemental videos

This video
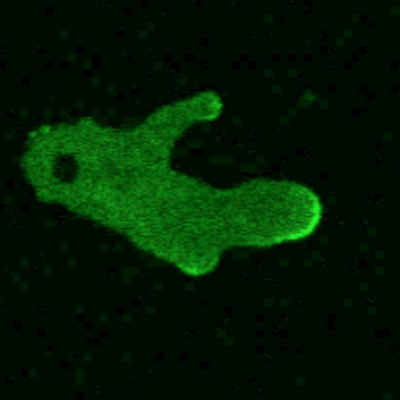

This video
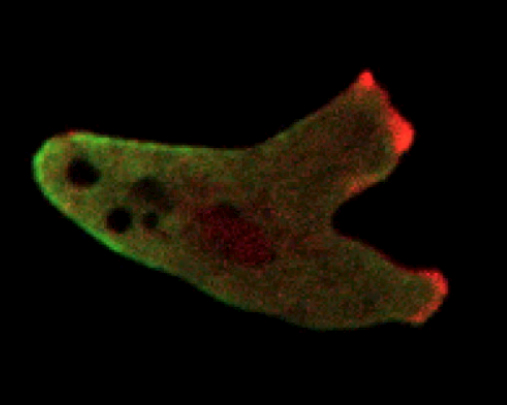
This work was supported by the National Institutes of Health.
References
1. K. F. Swaney, C.-H. Huang, P. N. Devreotes, Annu. Rev. Biophys. 39, 265 (2010). https://doi.org/10.1146/annurev.biophys.093008.131228
2. A. E. Carlsson, D. Sept, Methods Cell Biol. 84, 911 (2008). https://doi.org/10.1016/S0091-679X(07)84029-5
3. L. Song et al., Eur. J. Cell Biol. 85, 981 (2006). https://doi.org/10.1016/j.ejcb.2006.01.012
4. D. Fuller et al., Proc. Natl. Acad. Sci. USA 107, 9656 (2010); https://doi.org/10.1073/pnas.0911178107
see also M. Ueda, T. Shibata, Biophys. J. 93, 11 (2007). https://doi.org/10.1529/biophysj.106.1002635. H. C. Berg, E. M. Purcell, Biophys. J. 20, 193 (1977). https://doi.org/10.1016/S0006-3495(77)85544-6
6. W. Bialek, S. Setayeshgar, Proc. Natl. Acad. Sci. USA 102, 10040 (2005); https://doi.org/10.1073/pnas.0504321102
R. G. Endres, N. S. Wingreen, Proc. Natl. Acad. Sci. USA 105, 15749 (2008). https://doi.org/10.1073/pnas.08046881057. K. Wang et al., Phys. Rev. E 75, 061905 (2007). https://doi.org/10.1103/PhysRevE.75.061905
8. C. A. Parent, P. N. Devreotes, Science 284, 765 (1999). https://doi.org/10.1126/science.284.5415.765
9. A. Levchenko, P. A. Iglesias, Biophys. J. 82, 50 (2002). https://doi.org/10.1016/S0006-3495(02)75373-3
10. S. Zhang, P. G. Charest, R. A. Firtel, Curr. Biol. 18, 1587 (2008). https://doi.org/10.1016/j.cub.2008.08.069
11. K. Takeda et al., Sci. Signal. 5, ra2 (2012). https://doi.org/10.1126/scisignal.2002413
12. C. Janetopoulos et al., Proc. Natl. Acad. Sci. USA 101, 8951 (2004). https://doi.org/10.1073/pnas.0402152101
13. X. Xu et al., Mol. Biol. Cell 16, 676 (2004). https://doi.org/10.1091/mbc.E04-07-0544
14. A. Goldbeter, D. E. Koshland Jr, Proc. Natl. Acad. Sci. USA 78, 6840 (1981). https://doi.org/10.1073/pnas.78.11.6840
15. I. Hecht et al., PLoS Comput. Biol. 7(6), e1002044 (2011). https://doi.org/10.1371/journal.pcbi.1002044
16. Y. Xiong et al., Proc. Natl. Acad. Sci. USA 107, 17079 (2010). https://doi.org/10.1073/pnas.1011271107
17. H. Meinhardt, J. Cell Sci. 112, 2867 (1999);
L. Bosgraaf, P. J. M. Van Haastert, PLoS One 4(8), e6842 (2009); https://doi.org/10.1371/journal.pone.0006842
J. S. King, R. H. Insall, Trends Cell Biol. 19, 523 (2009). https://doi.org/10.1016/j.tcb.2009.07.00418. W. Ma et al., Cell 138, 760 (2009). https://doi.org/10.1016/j.cell.2009.06.013
More about the Authors
Herbert Levine is the Hasselmann Professor of Bioengineering at Rice University in Houston, Texas. Wouter-Jan Rappel is a research scientist in the department of physics at the University of California, San Diego in La Jolla. Both are members of the NSF-sponsored Center for Theoretical Biological Physics.




