The nearly perfect Fermi gas

It is hard to imagine that the most strongly interacting nonrelativistic system known is a quantum degenerate atomic Fermi gas comprising just a few hundred thousand spin-up and spin-down atoms in an optical trap. An external magnetic field controls the strength of the scattering between spin-up and spin-down atoms, which interact very strongly when the field is correctly tuned. Evaporative cooling in the optical trap efficiently brings the temperature down to the quantum degenerate regime, where the atomic momentum is so small that the de Broglie wavelength is comparable to the interatomic spacing and quantum statistics is important. Quantum degenerate, strongly interacting Fermi gases, first produced ¹ in 2002, are now widely studied. ² They provide model systems for tabletop studies of high-temperature superconductivity, neutron stars, and nuclear matter.

Remarkably, those supercold Fermi gases share a feature with an exotic soup of quarks and gluons, a quark-gluon plasma (QGP), that existed just microseconds after the Big Bang. Heavy ion collisions at Brookhaven National Laboratory’s Relativistic Heavy Ion Collider have produced a strongly interacting QGP that is 19 orders of magnitude hotter and 25 orders of magnitude denser than the Fermi gases (see and the article by Barbara Jacak and Peter Steinberg on page 39). Yet both substances exhibit similar so-called elliptic flow, a consequence of extremely low viscosity hydrodynamics. Figure 1 illustrates the phenomenon for an atomic gas of lithium-6.

Universal behavior and perfect fluidity

A pair of colliding spin-up and spin-down atoms interacts most strongly when its total energy is near that of a so-called Feshbach resonance (see the Reference Frame by Daniel Kleppner in Physics Today, August 2004, page 12 ). To achieve that condition, an experimenter tunes an external magnetic field so that the sum of the kinetic and magnetic-interaction energies of the colliding pair equals that of a bound dimer. Near resonance, the properties of the gas are universal—that is, independent of the details of the two-body interaction. (For a review of universal behavior in few-body systems, see the article by Chris Greene in Physics Today, March 2010, page 40 ).

In particular, a strongly interacting gas in the universal regime is scale invariant; its properties are determined by the density n and the temperature T, the same variables that determine the properties of a noninteracting ideal gas. The ground-state energy of a strongly interacting Fermi gas differs from that of a noninteracting one at the same density by a universal factor whose precisely calculated value is in close agreement with measurements from experiments worldwide. ^2,4

The normal, nonsuperfluid strongly interacting Fermi gas is of great interest because it might be a perfect fluid—one having the minimum value allowed by quantum mechanics for the ratio of shear viscosity to entropy density, η/s. Superfluids have very small viscosity, but η/s actually increases below the normal-to-superfluid transition temperature.

Dimensional analysis suggests a quantum viscosity scale with the appropriate units of momentum/area. A natural momentum scale is ħ/L, where ħ is Planck’s constant and L is the interparticle spacing, which also determines a natural area L ² . Thus the shear viscosity can be expressed as $\eta =\alpha \hslash /L^3=\alpha \hslash n$ . Here α is a dimensionless function of the temperature and density—that is, a function of the ratio of the thermal de Broglie wavelength to the interparticle spacing. For air, $\alpha \approx 6000$ , whereas for water, $\alpha \approx 300$ those high values reflect that the flow of air and water is governed by classical physics. But for liquid helium-4 near the superfluid transition (the so-called λ-point), $\alpha \approx 1$ , indicative of flow in the quantum regime. Recent theoretical viscosity estimates for a strongly interacting Fermi gas ⁵ suggest that $\alpha \le 0.2$ .

In 2005 Pavel Kovtun and colleagues applied string theory methods to relate a class of strongly interacting systems to “dual” weakly interacting systems (for additional detail, see the article by Clifford Johnson and Peter Steinberg on page 29). As a result of their studies, they conjectured that for those strongly interacting systems, η/s must have a minimum, nonzero value. ⁶ Typically, the entropy density is something like nk _B, where k _B is Boltzmann’s constant, so η/s may naturally be expressed in terms of the density-independent unit ħ/k _B. Kovtun and company’s conjectured inequality,

$\frac{\eta }{s}\ge \frac{1}{4\pi }\frac{\hslash }{k_B}$ ((1)) suggests a fundamental and measurable connection between hydrodynamic and thermodynamic properties of strongly interacting systems with extremely low viscosity. The strongly interacting Fermi gas can serve as a model system for which both the viscosity and entropy can be measured and the ratio compared with the string-theory bound. ^7,8 As an added bonus, such studies provide benchmarks for nonperturbative many-body theories.

Measuring entropy and energy

The temperature of a trapped gas is spatially constant, but the density varies. Thus $\eta /s=\alpha \hslash /(s/n)$ is not constant. Nonetheless, since s/n is the local entropy per particle, it is reasonable to estimate

$\frac{\eta }{s}=\frac{\hslash }{k_B}\frac{〈\alpha 〉}{S/k_B}$.((2)) Here S is the average entropy of the trapped gas particles; thermodynamic measurements can determine its value. The density-weighted average value of α in the trap, 〈α〉, can be estimated from hydrodynamic measurements.

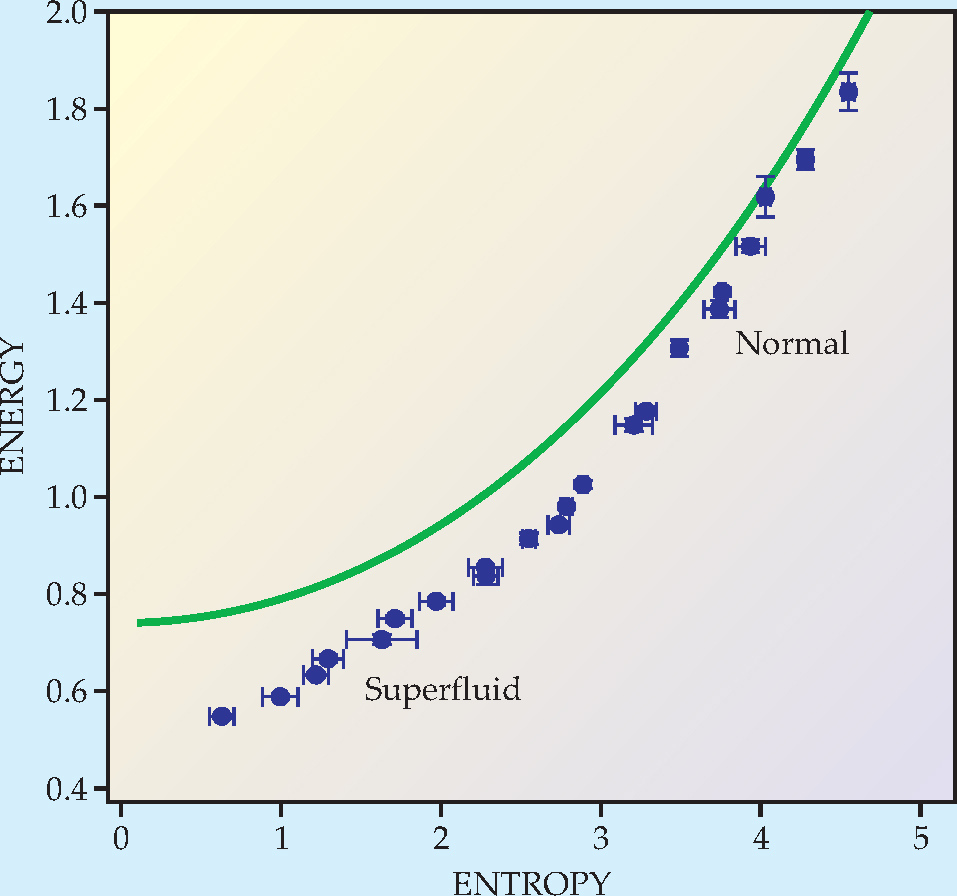
In part to characterize the entropy and viscosity of a normal strongly interacting Fermi gas, Le Luo, Bason Clancy, and I measured the entropy and the energy of a gas of ⁶Li atoms throughout the superfluid and normal fluid regimes. ⁴ Figure 2 shows a shift in the scaling of energy with entropy that signals a corresponding change in thermodynamic properties. The energy at which the scaling change occurs delimits the transition from superfluid to normal fluid. Entropy and viscosity measurements above that energy thus characterize normal fluid behavior.

A remarkable feature of strongly interacting Fermi gases in the universal regime is that the energy and entropy can be determined by simple measurements of trapped cloud sizes. Energy measurements are based on the virial theorem. At low temperatures, the optical trap that confines the atoms provides a nearly harmonic potential. Then the total energy $〈U〉:E=2〈U〉=3m{\omega }_z^2〈z^2〉$ . In giving the final equality, I have assumed an isotropic pressure so that the harmonic trapping potential energy is identical in the x, y, and z directions; by definition, z is the long direction in the cigar-shaped trap. Images such as those shown in figure 3 reveal the mean-square size 〈z ²〉.

The effective spring constant, $m{\omega }_z^2$ (m is the mass of a ⁶Li atom), may be precisely determined with parametric resonance. In that method, one varies the intensity of the trapping laser beam with a small-amplitude modulation whose frequency can be tuned. When the modulation frequency is twice that of a harmonic-oscillator frequency for the atoms in the trap, the energy of the atoms resonantly increases and, hence, so does the cloud size.

The conceptual simplicity of the energy measurement is, as earlier noted, a consequence of universal behavior. The gas generally contains condensed superfluid pairs, noncondensed pairs, and unpaired atoms, all strongly interacting; nonetheless, the mean-square size of the trapped cloud determines the total energy.

The key to measuring the average entropy S is to use an adiabatic sweep of a magnetic field to tune the system from the strongly interacting regime near the Feshbach resonance to a weakly interacting regime far from resonance. In that weak regime, the entropy S _W of the cloud is nearly that of an ideal Fermi gas in a harmonic trap, which can be calculated by elementary methods from the density of states and the entropy per state of an ideal gas at temperature T. The corresponding mean-square size of a weakly interacting Fermi gas 〈z ²〉_W is both calculable and measurable. The calculation establishes the link between the observable 〈z ²〉_W and the entropy S _W.

In our experiment, Luo, Clancy, and I had to verify that the magnetic-field sweep was adiabatic and, therefore, that the determined entropy S _W is the same as that in the strongly interacting regime. To do that, we performed a roundtrip sweep. Since, within experimental error, the energy after the roundtrip was the same as before the sweep, it follows that the sweep did not change the entropy.

As noted in the caption of figure 2, an observed change in the scaling of energy with entropy indicates the transition from superfluid to normal fluid. Fitting a smooth curve to the data, and using $T=\partial E/\partial S$ to get the temperature T, we find that the transition occurs at a rather high $T\simeq 0.2\hspace{0.17em}{T}_{\text{F}}$ , where T _F is the Fermi temperature. Although T _F is only about 1 µK in our experiments, and so the transition temperature may not seem high, in a condensed-matter system, where $T_{\text{F}}\approx {10}^4\text{K}$ , the corresponding superconductor transition would occur at 2000 K!

Estimating shear viscosity

Briefly releasing a strongly interacting Fermi gas from an optical trap and then recapturing it excites a “breathing mode” hydrodynamic oscillation in the cloud size. By measuring the damping time of those oscillations, one can estimate the gas’s shear viscosity and compare it with theoretical predictions. My colleagues and I combined estimates of the shear viscosity from damping measurements with entropy data to get the η/s ratio for ⁶Li. Our value ⁸ was comparable to that of liquid He near the λ point—significantly higher than the string-theory bound in equation (2). However, damping may arise from collisions between the hydrodynamically vibrating gas and the low-density ballistically moving gas at the trap edges that oscillates at a different frequency. That effect would increase the measured viscosity.

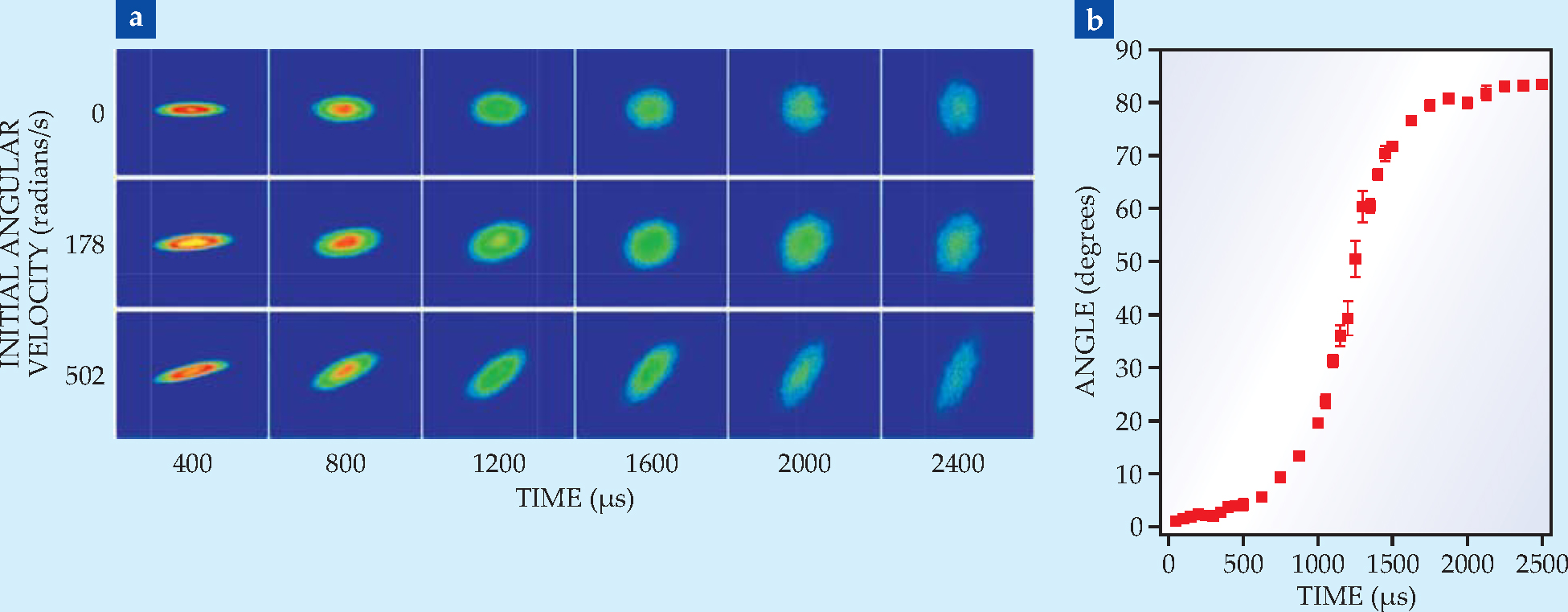
To investigate low-viscosity hydrodynamics in a trap-free environment, Clancy, Luo, and I studied the free-expansion dynamics of ⁶Li atoms released from a rotating optical trap. ⁹ We evaporatively cooled the gas to near its ground state and added a controlled amount of energy. Once the gas was released from the trap, we imaged its rotation over time; figure 4 shows typical data for a few initial angular velocities. As the gas expands, the angular velocity increases. That behavior is a consequence of the very low viscosity hydrodynamics and elliptic flow: As the cloud changes from cigar-shaped to more spherical, the moment of inertia decreases.

To estimate the viscosity, we began with an exact solution to the hydrodynamic equations absent viscosity and assumed that viscosity causes the observed slowing down relative to the zero-viscosity solution. After adding terms to the hydrodynamic equations that arise from shear viscosity, we found that the predicted slowing depends on the trap-averaged viscosity parameter, 〈α〉. The empirical data indicate that 〈α〉 increases as the initial energy of the trapped cloud is increased.

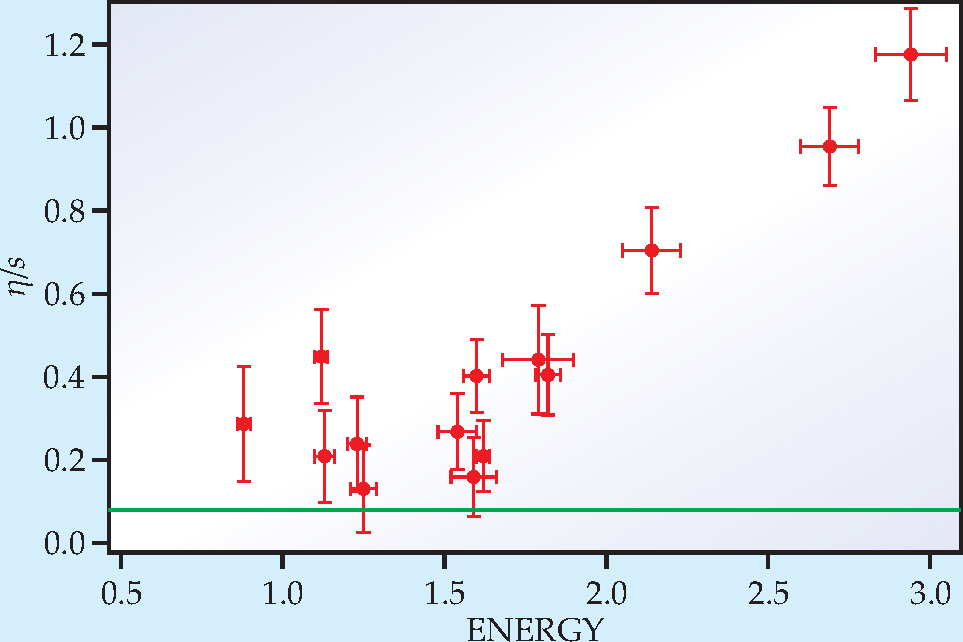
Combining the viscosity estimates from the rotating-trap experiment with the entropy measurements described earlier yields the η/s ratios shown in figure 5, which also indicates how close the measured ratios come to the conjectured lower bound. Our results suggest that a strongly interacting Fermi gas in the normal fluid regime may be a nearly perfect fluid.

Currently, my colleagues and I are developing model-independent methods for measuring shear viscosity. Combined with our model-independent measurements of the thermodynamic properties, viscosity data could offer new challenges for those doing state-of-the-art nonperturbative many-body calculations. Perhaps studies of strongly interacting gases will spur new developments in the application of string-theory methods to those fascinating systems; if so, we can look forward to a richer understanding of the deep connections between strongly and weakly interacting systems.