The Hund-metal path to strong electronic correlations
DOI: 10.1063/pt.wqrz.qpjx
Electrons in solids can behave independently from one another or as collective team players, whose interactions result in emergent cooperative phenomena such as magnetism, metal–insulator transitions, and unconventional superconductivity, to name a few. That team behavior happens in so-called strongly correlated materials that raise fundamental science questions, offer promising technological applications, and have given birth to a whole subfield of condensed-matter physics.

In weakly correlated materials, such as simple metals and semiconductors, electrons reside in extended orbitals and have a large kinetic energy. One can think of their quantum state in terms of independent waves that are delocalized through the solid and have an energy spectrum organized into bands. In contrast, electrons in strongly correlated materials reside in more localized orbitals; hence it is more natural to think of their quantum states in terms of correlated particles residing near the nuclei.
Strong-correlation phenomena abound not only in materials with partially filled d and f shells, such as transition metals, rare earths, and actinides, but also in organic materials where electrons reside in molecular orbitals. The degree of correlation is usually controlled by pressure, stress, or doping. Recently, multilayers of 2D materials, such as graphene and transition-metal dichalcogenides, were turned into strongly correlated systems by twisting or misaligning the layers and applying gate voltages. (See the article by Andrei B. Bernevig and Dmitri K. Efetov on page 38
Different families of materials follow distinct routes to strong-correlation physics. In so-called Mott insulator systems, the Coulomb repulsion of electrons impedes their motion and blocks their kinetic energy. Materials in the heavy-fermion family have two fluids of electrons, which live rather independent lives at high temperatures: mobile electrons and localized f electrons that form local magnetic moments. At very low temperatures, the hybridization, or quantum mechanical mixing, between those two species of electrons becomes relevant. Then a single fluid of itinerant, albeit slowly moving, “heavy” electronic quasiparticles emerges below a characteristic scale known as the Kondo temperature.
This article focuses on a new perspective that describes a broad family of materials whose properties cannot be understood within either the Mott or the heavy-fermion paradigms. Those materials display obvious signs of strong correlations, but unlike Mott systems, they have mobile electrons; unlike simple metals, they have local moments; and unlike heavy fermions, they involve a single fluid of electrons. As we describe below, a key concept needed to understand the puzzling materials is what’s known as Hund’s-rule coupling—the lowering of the Coulomb repulsion that accompanies the placement of two electrons of parallel spins in different orbitals. 1
The theory of what are now called Hund metals, a term coined in 2011,
2
was launched by two pioneering papers that applied dynamical mean-field theory to the study of the normal state of iron-based superconductors
3
(see the article by Qimiao Si and Nigel Hussey, Physics Today, May 2023, page 34
Researchers soon realized that a large, and still growing, family of compounds fits within the new paradigm. 2 , 5 Prominent members of that family are the ruthenium oxides, including the superconductor Sr2RuO4 and the antiferromagnet Ca2RuO4. Their puzzling thermodynamic and transport properties and intricate phase diagrams have been studied since the mid 1990s, but a consistent physical picture of their normal-state properties and the key role played by Hund coupling have only emerged in the past dozen years. 6
The modern development of the Hund-metal picture now explains the odd coexistence of itinerant and localized behaviors first noticed in photoemission studies of V5S8 by Atsushi Fujimori and coworkers 7 and has shed additional light on classic experiments showing enormous variations in the Kondo scale of different magnetic atoms embedded in a metallic host. 8 In this article we present in a pedagogical fashion the insights into Hund metals that have emerged. For a more detailed exposition, see review articles and references. 9 , 10
Atomic shells
An atomic shell with orbital angular momentum L has M = 2L + 1 orbitals corresponding to the possible values of the magnetic quantum number Lz. Orbital degeneracy is lifted by the crystalline environment and produces distinct subshells. Figure
Figure 1.

Excitations in three-orbital systems with (a) three electrons (a half-filled shell) in the ground state and (b) two electrons. Each electron is in a different orbital with parallel spins (bottom panels), in accordance with Hund’s rules. Removing or adding an electron produces a lower Hubbard band (LHB) and an upper Hubbard band (UHB) in the total density of states, plotted in the upper panels as a function of excitation energy E. The LHB and UHB are separated by an energy Ueff, the effective Coulomb interaction, which depends on the repulsion U for electrons in the same orbital and on the Hund coupling J, the energy change from aligning electron spins. For metals, the spectrum also contains low-energy quasiparticle (QP) excitations. When the Hund coupling is large, those excitations can overlap the Hubbard bands for non-half-filled shells. In such Hund metals, the QP peak has a substructure (inset).
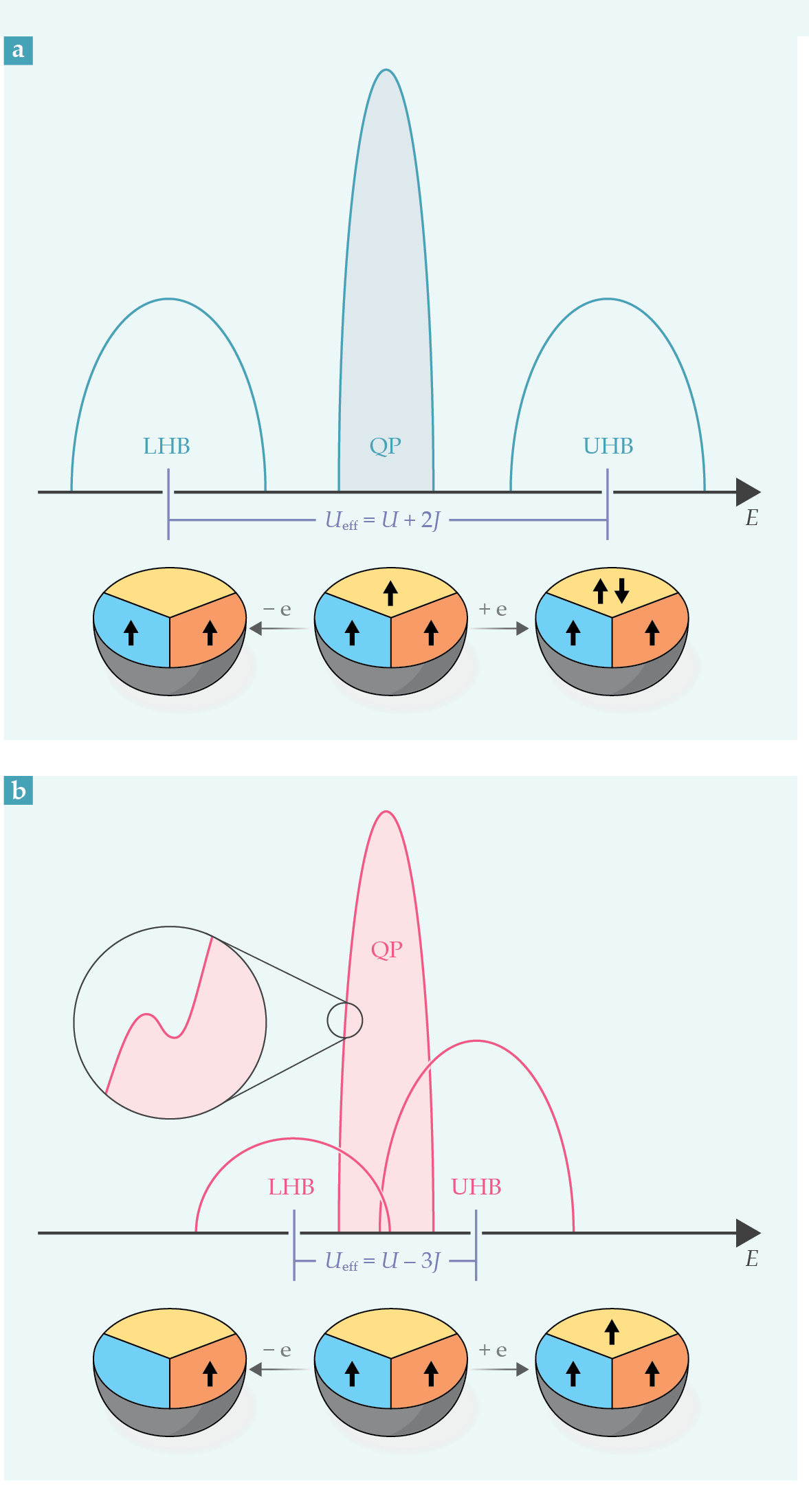
When two electrons with opposite spins occupy the same orbital, they feel the largest repulsive interaction U, the effective Coulomb interaction screened by the solid-state environment. By contrast, if two electrons occupy different orbitals, their effective repulsion is smaller—equal to an energy U′ < U if they have opposite spin, and equal to U′ − J when they have parallel spin. The Hund coupling J is the intra-atomic exchange interaction. Think of it as the energy gained by the material when its electron spins are aligned. When spherical symmetry exists, U′ ≃ U − 2J, and the interactions in decreasing order are U, U − 2J, and U − 3J.
Given the magnitude of those interaction terms, the lowest-energy configuration of N electrons in an atomic shell with M orbitals follows these rules: If N is smaller than M—that is, the shell is less than half filled—each electron occupies a different orbital and all have parallel spins, hence a total spin S = N/2. If N = M (a half-filled shell), all orbitals are singly occupied, with maximal spin S = M/2. And if N is larger than M, N − M orbitals must be doubly occupied, while the remaining spins are aligned, hence a total spin, S = M − N/2. Those statements illustrate the more general rules formulated in 1925 by Friedrich Hund. 1 For a simple picture of Hund’s rules, think of a bus with rows of two seats each. If possible, passengers (electrons) will typically spread out so that the seat next to them is empty.
The Hubbard energy U penalizes charge imbalance. It is the main player in Mott and heavy-fermion materials. It blocks charge motion, promotes localization in Mott systems, and reduces the hybridization in heavy-fermion materials. In Hund metals, by contrast, the Hubbard repulsion is too small to localize electrons. Those materials’ key parameter is J, which forces the electrons to adopt a collective configuration with the largest possible spin as they hop around and induces strong correlations. In a nutshell, Mott insulators, heavy-fermion compounds, and Hund metals are all correlated materials, but their electron correlations arise from constraints on charge, hybridization, and spin, respectively.
In a solid, an atomic configuration with one extra electron added to the ground state can move around. That excitation is known as the upper Hubbard band. Similarly, excitations with one less electron form the lower Hubbard band, as shown in figure
The so-called Mott gap between the lower and upper Hubbard bands is controlled by the energy cost Ueff = E0(N + 1) + E0(N − 1) − 2E0(N) required to transfer a single electron from one atom to another, where E0(N) is the atomic energy when the atom has N electrons. For a half-filled shell, one finds Ueff = U + 2J, and increasing the Hund coupling also increases the Mott gap. That explains why many materials with a half-filled shell are Mott insulators. But for a non-half-filled shell, Ueff = U′ − J ≃ U − 3J, and the Mott gap decreases when J is increased. As a result, J promotes metallicity by increasing the overlap between the Hubbard bands. Those effects were pointed out early on by Dirk van der Marel and George Sawatzky 11 and by Fujimori and colleagues. 7
In metals, additional excitations, called Landau quasiparticles, exist at low energy. Those quantum states are waves with a well-defined momentum that are delocalized throughout the solid. The occupied and unoccupied states are separated by a boundary in momentum space known as the Fermi surface. Interactions can strongly reduce the velocity of the quasiparticle states near the Fermi surface, which enhances the effective mass of the excitations.
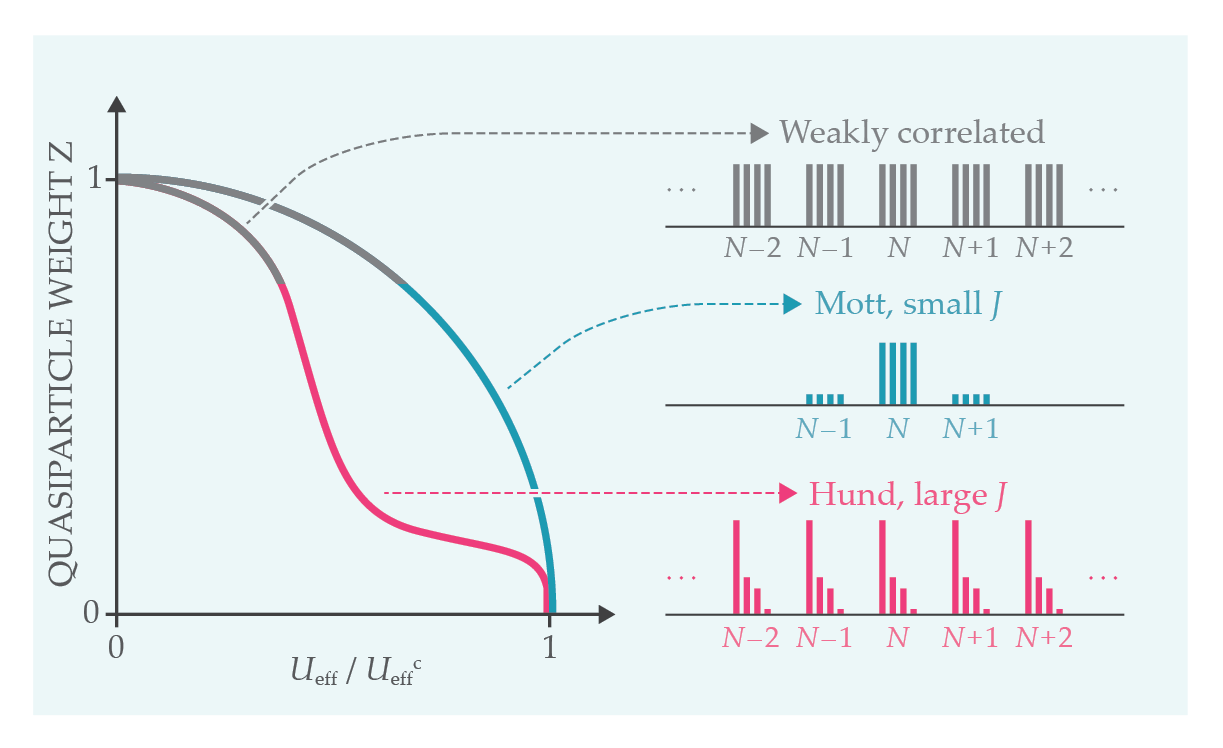
The quasiparticle weight Z is the probability of an electron being in a quasiparticle state when it is removed from (or added to) the ground state of the solid, as probed in photoemission. In a weakly correlated material, most of the excitations are quasiparticles, and Z is close to unity (see figure
Figure 2.

The quasiparticle weight Z—the probability that an electron removed or added to the ground state will be in a quasiparticle state—depends on Ueff /Ueffc, the ratio of the effective Coulomb energy Ueff to the critical value Ueffc at which the metal–insulator transition takes place. The plot compares three cases: a weakly correlated metal (gray), a strongly correlated metal close to the transition (blue), and a metal with substantial Hund coupling (pink). The Hund-metal regime has a characteristic plateau
Dynamical mean-field theory
For strongly correlated materials, a serious revision of the “standard model” of solid-state physics, which focuses solely on quasiparticles, is needed. Instead of adding correlations to an electron gas, a proper description of a correlated solid begins with the many-body eigenstates (so-called atomic multiplets) of individual atoms, which constitute a sizeable part of the excitation spectra at energies up to several electron volts.
Think of a strongly correlated material as a collection of atomic many-body systems that exchange electrons. That perspective is central to dynamical mean-field theory (DMFT). For reviews, see reference and the article by one of us (Kotliar) and Dieter Vollhardt, Physics Today, March 2004, page 53
DMFT focuses on the sequence of quantum jumps between electronic configurations of the atoms as electrons hop between them. It describes that process as the emission and absorption of electrons between an atom and an effective self-consistent bath representing the rest of the solid. The theory details whether, how, and when quasiparticles then emerge at low energy. In Sr2RuO4, for example, Landau’s Fermi-liquid regime—characterized by long-lived, coherent quasiparticles—is formed only below a temperature TFL ~ 25 K, which corresponds to an energy scale of about 2 meV.
Hund metals
Figure
The Hund coupling is two-faced: On the one hand, it pushes the Mott transition to larger values of U; on the other hand, it leads to an extended, strongly correlated metallic regime by decreasing Z and enhancing the quasiparticle effective mass. 5
A useful diagnostic of the different regimes is a histogram of the relative weights associated with each atomic configuration in the ground state of a given material. It is what an observer embedded in the solid at a given atomic site would record by measuring the time that an atom spends in each atomic configuration. As depicted in figure
Go with the flow
Figure
Figure 3.

Evolution of a material’s active degrees of freedom as a function of energy. It goes from a high-energy regime (top), in which atoms fluctuate between different atomic configurations, to a low-energy regime (bottom), in which coherent quasiparticle excitations emerge. The dynamical mean-field description of the process is depicted here as an onion-like sequence of effective energy shells added to the isolated atom, pictured at top. In Hund metals, the quenching of orbital and of spin fluctuations occurs at distinct temperatures Torb and Tsp, respectively. Between Torb and Tsp, the spin–orbital separated regime, the orbitals are quenched but a higher spin (S = 3/2 here) remains. At low energy, the so-called Fermi-liquid regime, all orbitals and spin states are effectively filled by an equal number of electrons so that the atomic degrees of freedom no longer fluctuate. A large diversity of symmetry-breaking instabilities and long-range orders, such as superconductivity and magnetism, may emerge out of either regime.
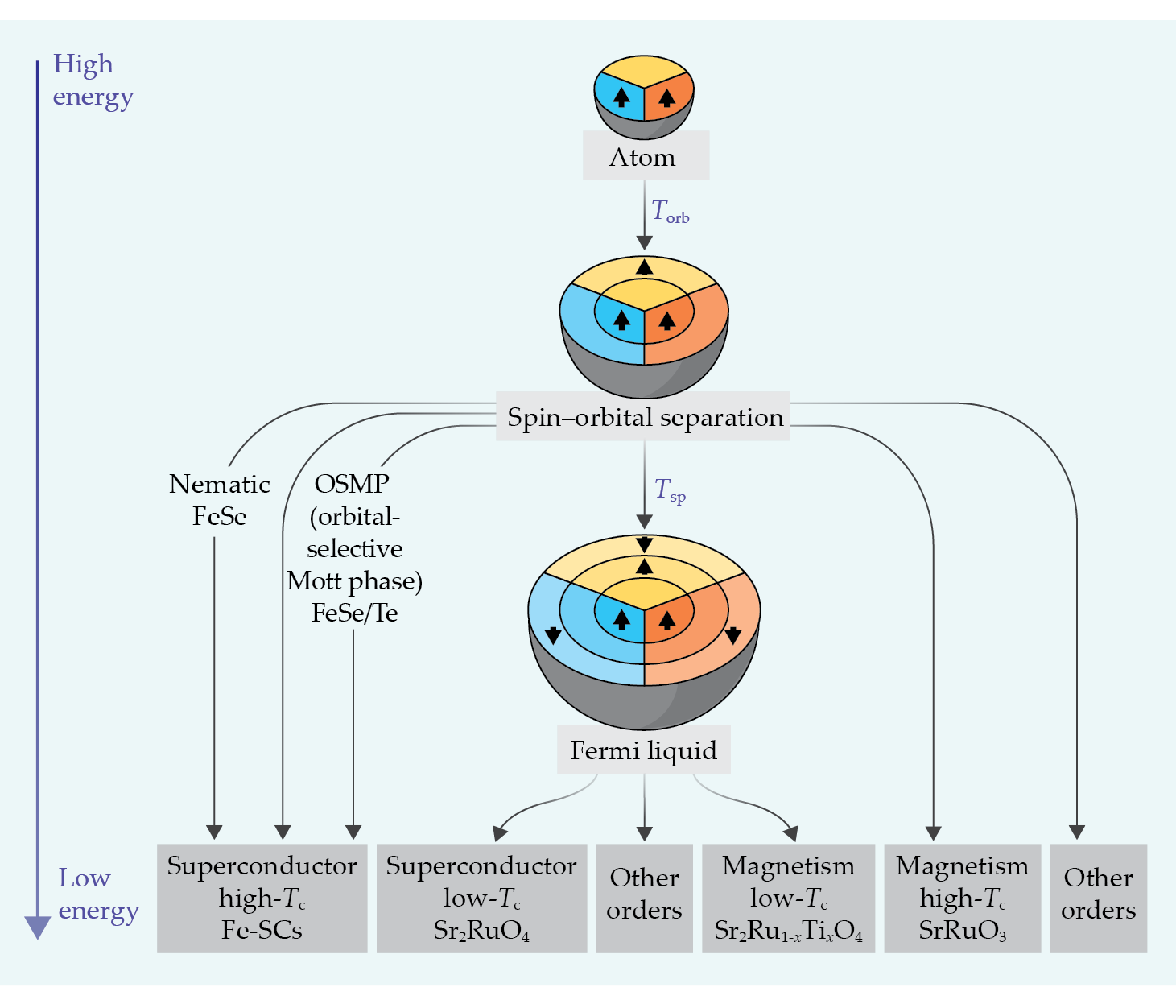
As illustrated in figure
In the SOS regime, which is a hallmark of Hund metals, the spins are quasi-localized, or “frozen” on intermediate time scales, 4 leading to a Curie–Weiss temperature dependence χ ~ 1/(T + T0) of the local magnetic susceptibility with a tiny value of T0. In contrast, the orbital and charge degrees of freedom are itinerant and the corresponding susceptibilities are temperature independent.
Smoking guns
Inelastic neutron scattering is an important experimental tool in the SOS regime because it directly probes the nature of the spin excitations. The frequency-dependent imaginary part of the spin susceptibility, averaged over wavevectors, is related to the density of states of spin excitations. Multiplying it by a Bose factor and integrating it over frequency gives the size of the fluctuating local moment. Figure
Figure 4.

Signatures of Hund metals. (a) The energy dependence of the momentum-averaged imaginary part of the magnetic susceptibility χ″ is shown for antiferromagnetic BaFe2As2 at T = 5 K and for 5% nickel-substituted BaFe2As2, a superconductor, at 5 K. Unlike the low-energy spectrum, the high-energy spectrum (above 80 meV) is only weakly doping dependent. (Adapted from ref.
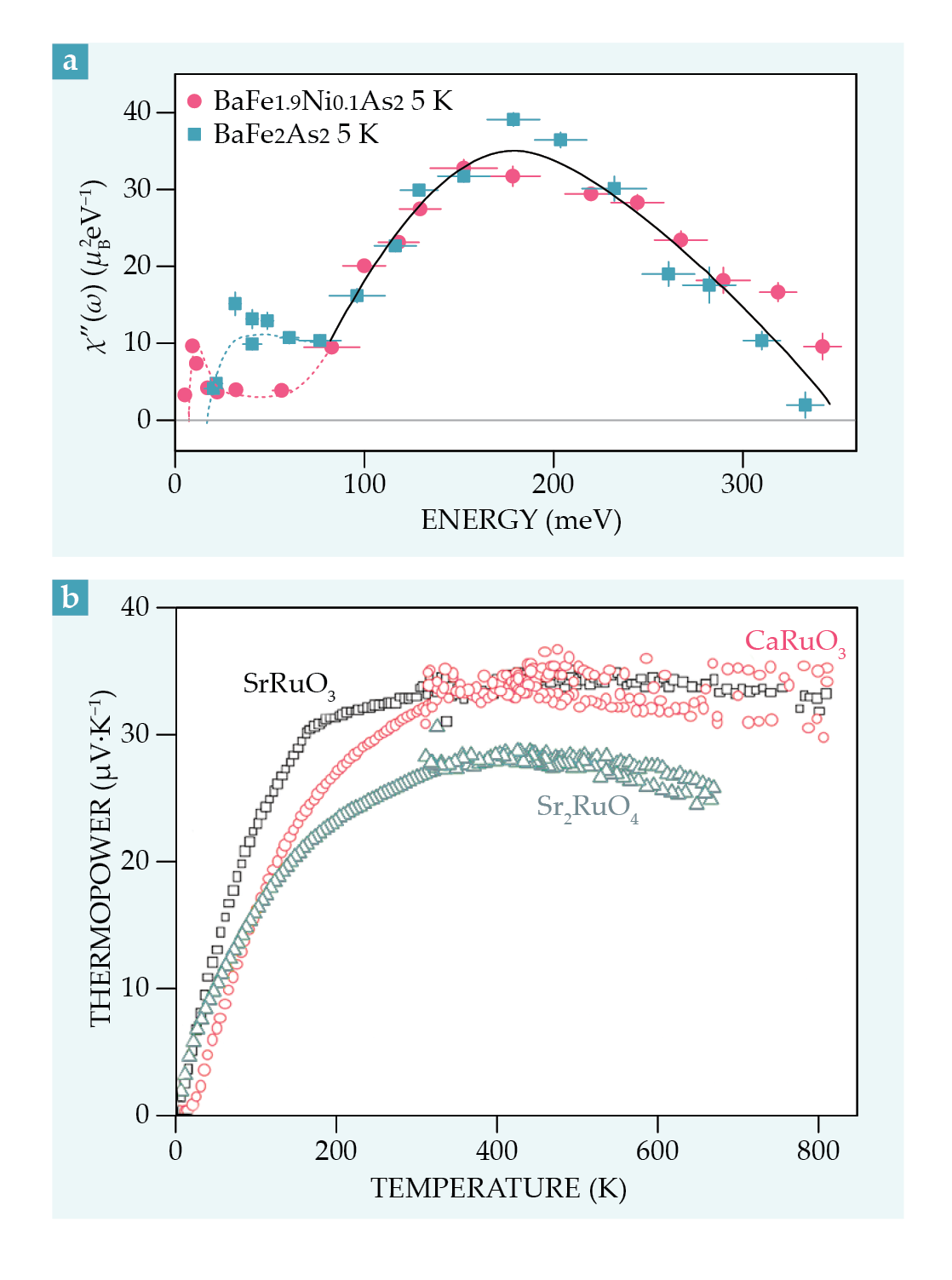
The high-energy part of the susceptibility and the fluctuating local moment do not vary much from one family member to another or as the temperature is changed. The low-energy part, however, displays a strong temperature and material dependence: Undoped BaFe2As2, for example, undergoes a transition to a stripe phase, whereas the nickel-doped compound becomes superconducting.
Those examples illustrate the large diversity of possible long-range orders at the low-energy end of the flow shown in figure
An example of the low-temperature instability is seen in Sr2RuO4: It undergoes a superconducting transition at Tc ~ 1.4 K, well below the onset of the Fermi-liquid regime at 25 K. Above TFL, the material enters the SOS regime. The ferromagnet SrRuO3 and the nematic superconductor FeSe are examples of materials that order above TFL.
At intermediate temperatures or energies, Sr2RuO4, SrRuO3, and other members of the ruthenate family display characteristic features of Hund metals. Resonant inelastic x-ray scattering measurements performed by Hakuto Suzuki and colleagues in Bernhard Keimer’s group at the Max Planck Institute for Solid-State Research in Stuttgart, Germany, in 2023 provide direct experimental evidence of the separation of energy scales associated with orbitals and spins in Sr2RuO4.
Evidence given by the Seebeck effect has shown that spins fluctuate in the SOS regime but orbitals do not. The effect measures the electrical potential drop when a sample is subject to a thermal gradient, and its value can be related to the entropy of fluctuating degrees of freedom in the material. The Seebeck coefficient of three ruthenates is shown in figure
As noted by Yannick Klein, Sylvie Hébert, and coworkers from the CRISMAT laboratory in Caen, France, and confirmed by DMFT calculations, 15 that value can only be explained by considering that the spin degrees of freedom fluctuate while the orbital ones do not. Hence spin entropy provides the only contribution to the Seebeck coefficient. Inelastic neutron scattering experiments also reveal the presence of fluctuating local moments in Sr2RuO4, as signaled by a component of the magnetic response that depends weakly on momentum. As shown by DMFT, these local spin fluctuations are associated with Hund physics. 16
Orbital differentiation
While the concept of Hund metals was emerging, it became clear that Hund coupling plays a key role in promoting orbital differentiation—the emergence of a large difference in the degree of correlations among otherwise similar orbitals. The phenomenon is especially relevant to iron-based superconductors.
17
Groups led by Séamus Davis and Zhi-Xu Shen observed it using different experimental probes—scanning electron microscopy and angle-resolved photoemission, respectively. Figure
Figure 5.

Orbital-selective phenomenon in FeTe1−xSex. (a) The material’s phase diagram as a function of dopant concentration x and temperature T. The two orange points mark the boundary of the orbital-selective Mott phase (OSMP), in which one orbital no longer hybridizes with the others. A lighter color indicates a lower degree of quasiparticle coherence. (b) The Fermi surface of FeTe0.56Se0.44 in momentum space at 15 K for the correlated metallic phase. (c) For FeTe at 80 K in the OSMP, pockets at the Fermi surface around the X point in the Brillouin zone emerge from the dehybridization of the dxy orbital. Those dramatic differences, which are produced by variations in x or T, are signatures of the orbital differentiation. (Images adapted from ref.
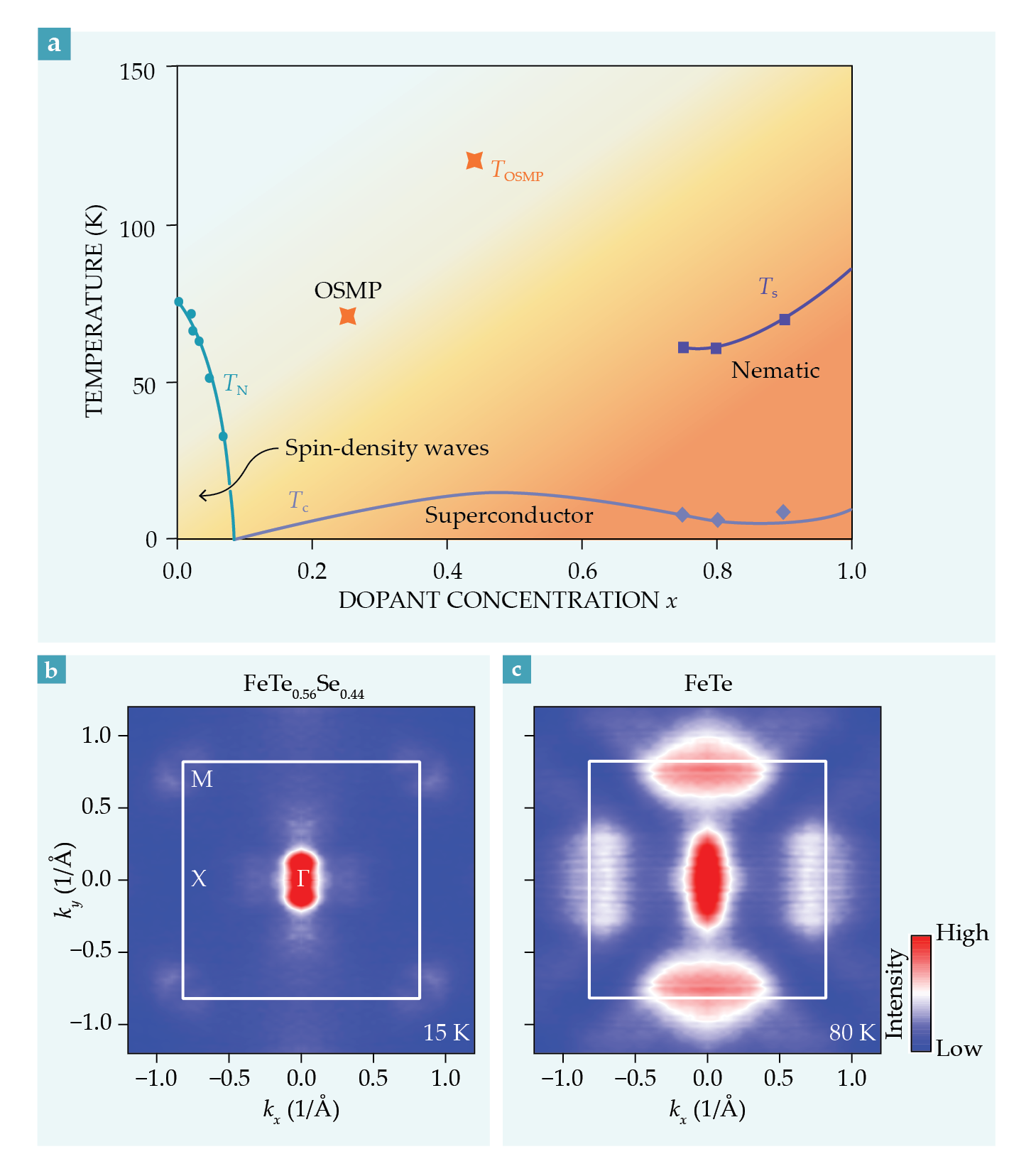
As the tellurium-rich end of the phase diagram is approached, the electrons residing in the dxy orbital become heavier and more incoherent than those in the other d orbitals, as predicted by DMFT calculations.
2
Eventually the system enters an orbital-selective Mott phase (OSMP), an extreme form of orbital differentiation in which the dxy orbital is so incoherent that its dispersion cannot be observed, while the other remaining d orbitals still form itinerant quasiparticle bands. The panels in figure
Outlook
The crucial role played by the Hund coupling in inducing strong electronic correlations is relevant to many more materials than the ones discussed in this article. Hund physics may actually occur in combination or in competition with other important factors, such as the proximity of a van Hove singularity—a region of momentum space with vanishing electronic velocity—as in Sr2RuO4, 9 and the emergence of Mott physics, for example, when iron-based superconductors are brought closer to a half-filled d5 shell by hole doping. 10
In all cases, it is essential to think in terms of the dynamical fluctuations between different many-body atomic configurations to describe Hund metals. They provide some of the most beautiful illustrations of the DMFT concept. As we have argued, DMFT provides a deep understanding of strongly correlated materials by describing the flow from fluctuations between atomic configurations at high energy to emerging, coherent quasiparticles at low energy.
Along with that conceptual framework and in combination with electronic-structure methods, DMFT offers a powerful framework to calculate and predict thermodynamic, transport, and spectroscopic properties of correlated materials, starting from their structure and chemical composition. Indeed, an extraordinary number of successful comparisons between experimental studies and materials-specific calculations by groups across the world have provided evidence of the crucial role of Hund physics.
The challenges for researchers are to understand how instabilities, such as high-temperature superconductivity, emerge out of a metallic state in which a description in terms of long-lived coherent quasiparticle excitations is not applicable and also to extend computational methods to reach lower energies and address fluctuations over long length scales.
We are grateful to Luca de’ Medici, Fabian Kugler, Jernej Mravlje, and André-Marie Tremblay for their suggestions and insightful comments, and to Pengcheng Dai, Sylvie Hébert, Jianwei Huang, Sinjie Xu, and Ming Yi for sharing their experimental data and helping to display them. We are also grateful to Lucy Reading-Ikkanda for creating the figures in the article.
References
1. F. Hund, Z. Phys. 33, 345 (1925). https://doi.org/10.1007/BF01328319
2. Z. P. Yin, K. Haule, G. Kotliar, Nat. Mater. 10, 932 (2011). https://doi.org/10.1038/nmat3120
3. K. Haule, G. Kotliar, New J. Phys. 11, 025021 (2009). https://doi.org/10.1088/1367-2630/11/2/025021
4. P. Werner et al., Phys. Rev. Lett. 101, 166405 (2008). https://doi.org/10.1103/PhysRevLett.101.166405
5. L. de’ Medici, J. Mravlje, A. Georges, Phys. Rev. Lett. 107, 256401 (2011). https://doi.org/10.1103/PhysRevLett.107.256401
6. J. Mravlje et al., Phys. Rev. Lett. 106, 096401 (2011). https://doi.org/10.1103/PhysRevLett.106.096401
7. A. Fujimori, M. Saeki, H. Nozaki, Phys. Rev. B 44, 163 (1991). https://doi.org/10.1103/PhysRevB.44.163
8. M. D. Daybell, W. A. Steyert, Rev. Mod. Phys. 40, 380 (1968). https://doi.org/10.1103/RevModPhys.40.380
9. A. Georges, L. de’ Medici, J. Mravlje, Annu. Rev. Condens. Matter Phys. 4, 137 (2013). https://doi.org/10.1146/annurev-conmatphys-020911-125045
10. L. de’ Medici, M. Capone, in The Iron Pnictide Superconductors: An Introduction and Overview, F. Mancini, R. Citro, eds., Springer (2017), p. 115;
K. Stadler et al., Ann. Phys. 405, 365 (2019). https://doi.org/10.1016/j.aop.2018.10.01711. D. van der Marel, G. A. Sawatzky, Phys. Rev. B 37, 10674 (1988). https://doi.org/10.1103/PhysRevB.37.10674
12. A. Georges et al., Rev. Mod. Phys. 68, 13 (1996). https://doi.org/10.1103/RevModPhys.68.13
13. C. Aron, G. Kotliar, Phys. Rev. B 91, 041110 (2015); https://doi.org/10.1103/PhysRevB.91.041110
A Horvat, R. Žitko, J. Mravlje, Phys. Rev. B 94, 165140 (2016); https://doi.org/10.1103/PhysRevB.94.165140
K. M. Stadler et al., Phys. Rev. Lett. 115, 136401 (2015). https://doi.org/10.1103/PhysRevLett.115.13640114. M. Liu et al., Nat. Phys. 8, 376 (2012). https://doi.org/10.1038/nphys2268
15. Y. Klein et al., MRS Online Proc. Libr. 988, 9880706 (2006); https://doi.org/10.1557/PROC-988-0988-QQ07-06
J. Mravlje, A. Georges, Phys. Rev. Lett. 117, 036401 (2016). https://doi.org/10.1103/PhysRevLett.117.03640116. P. Steffens et al., Phys. Rev. Lett. 122, 047004 (2019); https://doi.org/10.1103/PhysRevLett.122.047004
H. U. R. Strand et al., Phys. Rev. B 100, 125120 (2019). https://doi.org/10.1103/PhysRevB.100.12512017. L. de’ Medici et al., Phys. Rev. Lett. 102, 126401 (2009). https://doi.org/10.1103/PhysRevLett.102.126401
18. J. Huang et al., Commun. Phys. 5, 29 (2022). https://doi.org/10.1038/s42005-022-00805-6
More about the authors
Antoine Georges is a professor of physics at the Collège de France in Paris and director of the Center for Computational Quantum Physics of the Flatiron Institute, Simons Foundation, in New York City. He is also affiliated with the University of Geneva in Switzerland and École Polytechnique in Palaiseau, France. Gabriel Kotliar is a Board of Governors Professor of physics at Rutgers University in Piscataway, New Jersey, and is also affiliated with Brookhaven National Laboratory.






