The formation and differentiation of Earth
DOI: 10.1063/PT.3.1362
The solar system began to form 4568 million years ago, from a disk of dust and gas around the young Sun. Within a few million years, Jupiter and Saturn had formed and the terrestrial planets had reached significant fractions of their present size. The processes by which the planets formed are of particular interest at a time when the search for Earth-like planets around other stars occupies considerable attention. Earth-like exoplanets somewhat larger than our own are already detectable, and criteria are being developed to identify stars around which smaller Earths should be present. 1
As rocky planets grow by accreting surrounding material, they suffer increasingly violent collisions. Figure 1 imagines a collision between a growing Earth-like planet and a smaller planetary embryo. One such encounter at the end of Earth’s accretion is thought to have created the Moon.

Figure 1. Artist’s impression of a collision between a growing Earth-like planet and a smaller planetary embryo. (Courtesy of NASA.)

In the context of our own solar system, a combination of computer simulations, high-pressure laboratory experiments, and mass spectrometry has led in recent years to a narrow range of models capable of satisfying the known constraints on planetary formation and growth. To understand those results, it is necessary to begin with the chemical composition of the solar system.
The composition of Earth and the solar system
Because the Sun constitutes 99% of the solar system’s mass, solar composition, obtained from spectroscopic measurements, represents the best estimate of solar-system composition. Spectroscopic studies of nearby stars have found several with Sun-like composition that also host planets. 1 Those stars also probably retain the composition of the protostellar nebulae from which their planets formed.
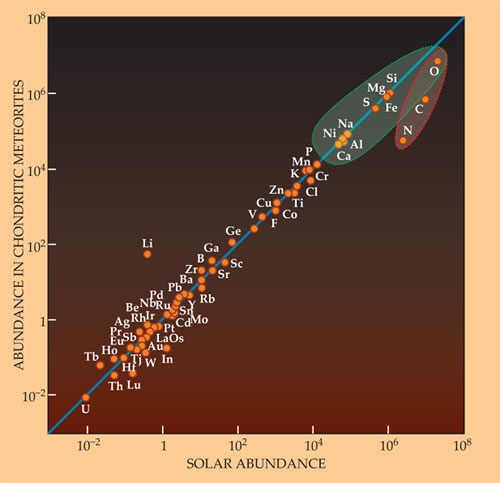
In our own solar system, detailed studies of meteorites have shown that one rare class of carbonaceous meteorite (the CI carbonaceous chondrites; the I is for the prototype Ivuna meteorite) has—with the exception of the most volatile elements such as hydrogen and helium—a chemical composition that’s almost exactly solar (see figure 2). Those meteorites represent undifferentiated protoplanetary material left over, in small asteroids, from the process of planet formation.

Figure 2. Plotting the elemental abundances in the Sun’s surface against those found in CI carbonaceous chondrites shows that those most primitive meteorites are, for the most part, reliably representative samples of the solar system’s makeup—other than hydrogen and helium. That’s certainly true of the nine elements (in the blue oval) that account for most of the mass of its rocky bodies. The adjacent orange oval encloses three elements somewhat depleted in the meteorites because they form ices that inhibited accretion into the early asteroids. Lithium is a conspicuous outlier because it is destroyed by fusion in the solar core. (Adapted from ref.
Earth, by contrast, is a highly differentiated body with a metallic core surrounded by a rocky silicate mantle and its crust. We cannot sample the core, but analysis of rocks lets us estimate the bulk composition of “Silicate Earth”—the mantle and crust. Figure 3 shows a plot of element concentrations in bulk silicate Earth, divided by those in the CI chondrites and normalized to correct for Earth’s paucity of the most volatile elements. The elemental ratios are plotted as a function of refractory character—that is, resistance to vaporization. Some refractory elements, such as Ca, Al, Sc, Ti, and the rare earths, are called lithophile (rock loving) in the sense that they concentrate in rocky silicate and are not easily leached out by molten iron.

Figure 3. Abundances of elements in Earth’s silicate crust and mantle, normalized to abundance in CI chondrite meteorites, are plotted against each element’s volatility, as measured by the condensation temperature Tc at which 50% of its atoms in the protoplanetary gas disk would have condensed. Elements with high Tc and therefore low volatility are called refractory. Their readiness to dissolve in molten iron is color-coded as siderophile (iron loving) or lithophile (rock loving). The figure shows increasing depletion in Earth’s crust and mantle (relative to the meteorites) with increasing volatility and siderophilia. (Adapted from ref.
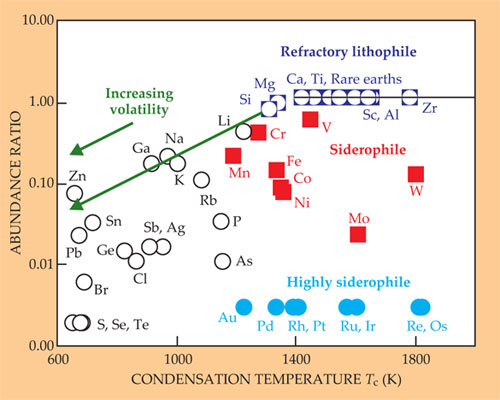
Refractory lithophiles are present in Silicate Earth in the same relative proportions as in the CI chondrites and the Sun. That similarity strongly implies that Earth as a whole has solar (chondritic) relative abundances of all the refractory elements, including the iron-loving siderophiles, which were swept down into the core by molten iron. As far as we can tell, the same applies to the Moon and Mars. Depletions in Silicate Earth of refractory siderophiles such as Ni, W, Mo, Re, Os, and iron itself are due to partial extraction of those elements into the core. The extent of that extraction can be estimated simply by comparing their concentrations in Silicate Earth with those of refractory lithophiles. The degree of extraction of individual elements helps establish the conditions under which Earth accreted and segregated its core.
The left side of figure 3 shows a decreasing relative abundance of elements in Silicate Earth with increasing volatility, which demonstrates that Earth is depleted in volatile elements relative to the chondritic reference. That depletion may reflect an approximately constant depletion of volatiles throughout Earth’s accretion (referred to as “homogeneous accretion”) or, more plausibly, an early accretion phase of very strong depletion followed by a progressive increase in the volatile-element contents of accreted materials as Earth approached its current size. That’s the competing “heterogeneous-accretion” scenario.
The growth of Earth
The planets of the solar system originated as dust and gas in the young Sun’s protoplanetary disk. The mechanisms of initial growth toward large bodies are poorly understood. But some combination of mechanical sticking and eventually gravitational perturbation must have formed many 10-km-sized objects in the first 104–105 years. 2 At that size, gravitational perturbation becomes the dominant mechanism for further accretion through collision. Although some planetesimals would have been destroyed in collisions, others would have continued to accrete.
Many-body model simulations show that once a population of larger planetary embryos emerged, they accreted rapidly at the expense of smaller objects in a period of runaway growth that was driven by dynamical friction—the preferential slowing of the most massive objects by energy equipartition—and the consequent gravitational focusing on those objects. Thus gravitational interactions led to a period of oligarchic growth. The few tens of planetary embryos that survived that period of about 1 million years were objects with masses a few percent of Earth’s.
Overall, Earth’s growth appears to have had an approximately exponential time dependence F(t) = 1 – e–t/τ, where F is the fraction of the planet’s completed mass at time t and τ is the characteristic time constant of order 10 million years. So the final stages of Earth’s accretion were relatively slow. They were presumably accompanied by scattering of planetary embryos inward and outward in the solar system, yielding a sequence of progressively more violent accretion impacts. 3 (See figure 1.)
We can calculate from the composition of Silicate Earth how different siderophile elements distributed themselves between the silicate mantle and the metal core as Earth grew. The partitioning of elements such as nickel and cobalt can then be compared with laboratory partitioning measurements to determine the conditions under which the core actually separated.
There are basically two extreme models that bracket the range of plausible scenarios of how Earth accreted and its core formed. Model A asserts that accreting planetesimals and embryos broke apart and re-equilibrated with Silicate Earth as their metal components liquefied and descended to the core. Model B asserts that accreting embryos merged their cores with Earth’s core and their silicate parts with Earth’s silicate regions, in particularly violent impacts of Earth with larger bodies, and there was no further reaction between the core and silicate phases.
It’s been known for nearly 50 years that model B cannot entirely explain the siderophile-element abundances remaining in Silicate Earth because those abundances cannot have been completely inherited from small bodies with low internal pressure. 4 More recently, high-pressure experiments have shown that the partitioning of Ni and Co between core and Silicate Earth can only be explained if the core separated out at very high pressures—greater than 25 gigapascals, which is the pressure at a depth of 700 km in the full-grown Earth. 5 This means that, as asserted by model A, there was substantial re-equilibration of metal and silicate at great depth in the forming Earth.
The apparently very high pressures of core formation have led to the “deep magma ocean” model of early Earth, as illustrated in figure 4. A deep layer of molten rock is attributed to heating by impacts and, at the earliest stages, by the decay of short-lived radionuclides. Arriving planetesimals and embryos disaggregate, and their metal components fall through the molten silicate, continually reacting with it until they reach a depth below which the silicate is solid. The metal ponds at that depth until the ponding layer is thick enough to become gravitationally unstable. At that point the metal descends rapidly to the core in great blobs about 100 km wide.

Figure 4. Deep magma ocean model of core formation. The high pressures required by partitioning of siderophile elements from Earth’s mantle to its core imply that iron descended in droplets through a deep molten silicate layer, equilibrating with the silicates as they fell. Because the pressures are much lower than at the core–mantle boundary, it’s conjectured that the molten iron and siderophile elements dissolved in it formed a pond shell at some intermediate depth where there was a transition from molten to solid silicate. The dense metal-pond layer eventually became gravitationally unstable so that large metal blobs descended to the core. (Adapted from ref.
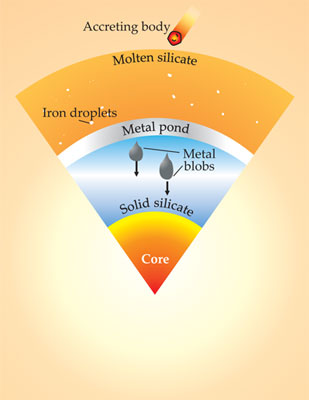
So goes the simplest version of the re-equilibration model A that’s compatible with the estimated high pressure of metal–silicate equilibrium partition. The deep-magma-ocean model has been extended to take account of the continuous process of core formation during accretion and the partitioning of many other elements (for example, tungsten, chromium, lead, copper, niobium, and manganese) between metal and silicate during the segregation of the core. The general conclusion is that pressures in the segregation region reached about 30–40 GPa and that Earth started in the inner solar system as a small body with a high ratio of metallic to oxidized iron. Then as it grew, Earth became more oxidized by accreting oxidized, volatile-rich materials from farther out in the solar system. 6 The evidence thus points to the heterogeneous accretion of Earth from materials that became progressively more oxidized and richer in volatiles. That model, first proposed by Heinrich Wänke in 1981, is consistent with the results of later many-body model simulations. 3
Recent attempts to model the accretionary process have relaxed the constraint of complete equilibrium and have allowed a mixture of equilibrium (model A) and nonequilibrium (model B) accretion. 7 The conclusions are still, however, basically the same: Earth became oxidized as it accreted, and it grew a substantial part of its core at high pressures.
Radioactive dating
In 1946 Fritz Houtermans and Arthur Holmes independently used the radioactive decays of uranium-235 (half-life 7 × 108 yr) and -238 (4.5 × 109 yr) to their stable lead daughters to show that Earth is at least 3.4 × 109 years (3.4 Gyr) old. Using the same basic method a decade later and assuming that Earth and various meteorites were formed from the same initial reservoir of U and Pb, Clair Patterson arrived at an age of 4.55 Gyr for Earth and the solar system. 8 The current meteoritic estimate of the solar system’s age is almost unchanged at 4.568 ± 0.001 Gyr. Earth, however, does not have one single age of formation. It appears to have formed over a period of about 100 Myr from the beginning of the solar system.
In addition to U–Pb, several long-lived radioactive systems, such as 87Rb–87Sr and 147Sm–143Nd, have been used to determine the ages of rocks and components in meteorites. And recent important advances have come from the discovery that many short-lived radionuclides were present at the origin of the solar system (
| Short-lived radionuclides present in early Earth | |||
|---|---|---|---|
| Parent | Daughter | Parent half-life (megayears) | Extinct after (megayears) |
| 182Hf (lithophile) | 182W (siderophile) | 8.9 | 45 |
| 107Pd (very siderophile) | 107Ag (siderophile) | 6.5 | 35 |
| 26Al (lithophile) | 26Mg (lithophile) | 0.7 | 3.5 |
| 146Sm (lithophile) | 142Nd (lithophile) | 103 | 500 |
| 60Fe (siderophile) | 60Ni (siderophile) | 1.5 | 7.5 |
| 129I (lithophile) | 129Xe (atmophile) | 15.7 | 80 |
The daughters of some of the early short-lived radionuclides (generated presumably in then-recent supernovae) can be used to determine the timing of events that occurred within about five parental half-lives of the solar system’s beginning. Their usefulness comes not only from the parents’ short lives but also from the differing chemical properties of them and their daughters, as shown in the table and in figure 5.

Figure 5. The isotopic ratio of two stable tungsten isotopes, 182W and 184W, measured in different systems, determines the time at which a planet’s core separated from its silicate mantle—assuming core formation was abrupt. Tungsten-182 is produced by the (9-Myr half-life) decay of the now extinct hafnium-182. Because Hf is lithophile, an iron core forming in a body of chondritic Hf/W abundance has its W isotopic ratio frozen in time because the core contains no Hf. By contrast, the silicate mantle goes on to evolve a W isotopic ratio higher than that in chondrites. The horizontal axis marks time since the solar system’s beginning. After about 50 Myr, the W isotopic ratio no longer grows in the mantle or the chondrites because there’s no more 182Hf left.
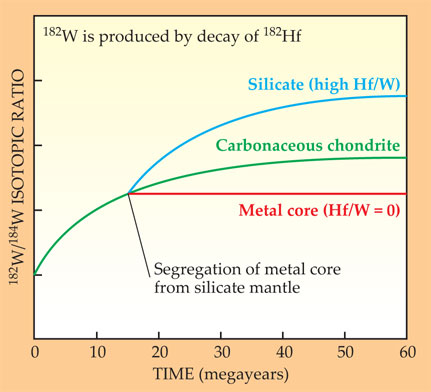
Figure 5 illustrates the use of the extinct radionuclide 182Hf and its daughter 182W to determine the time at which the metallic core separated in a planetary body. Chemically, both mother and daughter are refractory and therefore presumed to have been present in the same relative abundances in the planet before core separation as in primitive carbonaceous chondrites. In any planet having a chondritic Hf/W ratio, the proportion of the stable decay product 182W increases with time relative to other stable but nonradiogenic tungsten isotopes such as 184W. The W isotope ratio serves as the example in figure 5.
If now an iron core separates in the planet, there will be strong chemical fractionation of W from Hf, with siderophile W mostly entering the core and lithophile Hf remaining entirely in the rocky silicate layer. From then on, the core’s 182W/184W ratio remains constant because it has no 182Hf to decay to 182W. The silicate layer, by contrast, contains all the Hf and very little 184W. So in that layer, the 182W/184W ratio increases more rapidly by radioactive decay than it did in the initial mix. After five half-lives, the 182Hf is essentially extinct, so that the W isotope ratio levels off to a constant value.
Sampled now, 4.5 Gyr later, the difference between the W isotope ratio in the planet’s silicate (or metal) region and that of the carbonaceous-chondrite reference gives the age of core formation—provided one knows the preseparation concentration of 182Hf. And one can get that from the slope of the dependence of the W isotope ratio on the Hf/W chemical-abundance ratio in the chondrites. Applying this chronometry to the inner solar system leads to times of core formation after t0, the origin of the solar system, of about 2 Myr for small asteroids, 7 Myr for Mars, and 30 Myr for Earth. 9
Of course, such chronometry assumes that core segregation was a single-step event, and we have already discussed its probably continuous nature as Earth grew. The extreme continuum model A asserts that each increment of metal added to Earth was promptly partitioned between the outer silicate layer and the inner core in equilibrium proportions appropriate to the prevailing temperatures and pressures. Then the 182W data for Silicate Earth imply an exponential time constant τ for Earth’s growth of about 11 Myr. So assuming continuous exponential accretion and core formation, one would conclude that Earth was 63% formed 11 million years after t0, the beginning of the solar system, and 93% formed by 30 million years.
Many of the other extinct radionuclides may be used in similar ways to determine the times of other events in Earth’s formation. (
On the other hand, the relative abundances of different Ag isotopes in Silicate Earth are precisely chondritic, which means that the Ag we find in the crust and mantle developed its isotopic composition in an environment in which the Pd/Ag ratio was chondritic. Given that observation and the 182W data, one concludes that Ag and similar volatile solids were added to Earth after its first 30 Myr—that is, toward the end of accretion rather than throughout the planet’s formation.
Of the other short-lived isotopes, the decay of 129I to the atmophile (air loving) gas 129Xe has been used to suggest that Earth’s atmosphere lost volatile elements for the first 100 Myr. 11 And the much slower alpha decay of 146Sm to 142Nd has been used to trace the formation chronology of Earth’s earliest crust.
Origin of the Moon
Our moon is unusual among solar-system satellites because it has a relatively large mass—more than 1% of the mass of the planet it orbits. Theories for the Moon’s origin include capture, fission from the parent Earth, co-accretion during planetary growth, and generation by a colossal impact. All but the last can be excluded on dynamical or compositional grounds. That leaves the current favorite, visualized in figure 1: a collision between the growing Earth and a Mars-sized body toward the end of accretion. 12 Unlike the other theories, such a giant impact could account for the angular momentum of the Earth–Moon system.
That scenario can also explain many of the chemical similarities and differences between the two bodies. For example, Moon rocks show depletions of siderophile elements similar to what one finds in terrestrial rocks. And the Moon rocks have the same W isotopic ratio as Silicate Earth, indicating that they formed on a body with a core. But unlike Earth, whose core is 32% of its mass, the Moon has little or no core. In simulations in which Earth is struck a glancing blow by a Mars-sized body, the core of the impactor is left in the larger planet while the Moon is formed principally from silicate debris. That would explain its siderophile-element pattern, W-isotopic signature, and the lack of a lunar core.
The main problem with current simulations of the giant impact hypothesis, however, is that the Moon is chemically and isotopically much more like Earth than it ought to be. The simulations indicate that about 80% of the silicate debris that goes to form the Moon actually comes from the impactor. This means that the Moon should be chemically and isotopically distinct from Earth. But in addition to the W-isotopic system, all other elements for which we have data are identical isotopically on Earth and the Moon. (See PHYSICS TODAY, February 2008, page 16
That striking identity was first observed for oxygen isotopes, which vary considerably among Earth, Mars, and the different meteorite groups, but not between Earth and the Moon. The most logical explanation is that the Moon actually represents the silicate part of Earth at the time of the giant impact rather than the silicate part of the impactor. But how can we bring that suggestion into line with simulations that generate most properties of the Earth–Moon system but indicate the exact opposite for the source of lunar materials? To resolve this conundrum, various groups are exploring the nature of the impact and properties of the impactor.
What we do and don’t yet know
Asteroidal bodies started to form in the inner solar system 4568 Myr ago and grew into the terrestrial planets over tens of millions of years. In the case of Earth, the short-lived 182Hf–182W system indicates that the planet formed and segregated a core on a time scale of at least 30 or 40 Myr.
Chemical analysis of Earth’s silicate outer layers shows that they, in common with Mars and the Moon, are very similar in composition to primitive carbonaceous meteorites. That observation lets us estimate how different chemical elements distributed themselves between the iron-rich core and the silicate mantle as the core segregated.
High-pressure, high-temperature laboratory measurements of partitioning have yielded powerful constraints on the conditions under which Earth accreted external material. First, partitioning between core and mantle can only be reproduced if pressures were extremely high (30–40 GPa). It follows that metal and silicate substantially re-equilibrated in the growing Earth and that partitioning was not inherited from already-partitioned, low-pressure accreted bodies. Second, core–mantle partitioning is most readily reproduced if Earth started as a small, chemically reduced body and became more oxidized as accretion progressed.
That heterogeneous-accretion scenario 13 invokes the accretion of more oxidized, volatile-rich materials as Earth’s feeding zone expanded with its increasing mass to include volatile-rich materials from farther out in the solar system.
The Moon formed by the giant impact of a Mars-sized body on Earth some time before the oldest Moon rocks were formed (150 Myr after t0). Current models that reproduce the properties of the Earth–Moon system suggest that the debris that formed the Moon came predominantly from the impactor.
As might be anticipated, the above account has glossed over many big questions, some of the more important of which are as follows:
• The Moon is chemically and isotopically so much like Silicate Earth that it’s hard to accept that it was formed predominantly from the impactor rather than from Earth itself. So, is there some way in which the Moon can be formed principally from Earth while preserving the angular momentum of the Earth–Moon system? The answer will require more detailed dynamical simulations.
• How old is the Moon? It’s obviously older than the oldest Moon rocks, but there’s no current constraint on how much older it might be. Until recently it was believed that the 182Hf–182W system provided a limit of 45 Myr after t0, but that has now been called into question. 14 So constraining the lunar age requires better understanding of the Hf–W system on the Moon and Earth.
• Could the time scale of planetary accretion be much longer than that estimated from the Hf–W data? I have presented a time scale of 30–40 Myr for Earth and about 7 Myr for Mars. But that’s based on the assumption that each increment of metal added to the planet during accretion completely re-equilibrated with the outer silicate part. We do know from partitioning studies that there must have been substantial re-equilibration. But significant disequilibrium during energetic impacts cannot be excluded. The greater the degree of disequilibrium, the longer must have been the accretion time scale. The question can only be resolved by better experimental data on metal–silicate partitioning, particularly under the very high pressures relevant to the last stages of accretion, and by better information on the behavior of radioisotope systems during accretion.
• When were moderate volatiles such as Pb and Ag added to Earth? Before the wholely refractory 182Hf–182W system became technically accessible about 15 years ago, the long-lived (refractory–volatile) U–Pb system was used to estimate the accretion time scale. Although the U–Pb system is geologically complicated, it suggests that Earth’s Pb was fractionated from U about 100 Myr after t0. If the fractionation was due to Pb extraction to the core, 15 then the time scale of accretion was more protracted than implied by the Hf–W data, indicating substantial disequilibrium—that is, merging of pre-existing cores—during accretion of impacting planetesimals. On the other hand, it has been suggested that the moderately volatile elements were added to Earth only at the end of accretion and that the U–Pb age estimate is simply measuring that latest accretion event during heterogeneous accretion of Earth. 16 The 107Pd–107Ag data strongly support addition of volatile Ag toward the end of accretion but not necessarily after core formation ceased. 10 So, is U–Pb controlled by core formation, late volatile addition, or both? To answer that question, we need data on other short-lived radioactive systems involving volatiles and on the behavior of volatile elements during core formation.
• Did all the terrestrial planets undergo the same kind of heterogeneous-accretion path? Earth’s path from highly reduced to oxidized, with increasingly abundant volatiles, may be the normal one. We don’t know. But if it is, it’s applicable to understanding the formation of Earth-like planets in other stellar systems. The answer lies on Mars, from which we have some meteorites, chemical data from the Mars rovers, and—in the not-too-distant future—the return of actual surface samples.
Acknowledgments: My research has been supported by the Australian Research Council, the UK Natural Environment Research Council, the UK Science and Technology Facilities Council, and the European Research Council.
References
1. S. C. Schuler et al., Astrophys. J. Lett. 737, L32 (2011). https://doi.org/10.1088/2041-8205/737/2/L32
2. J. E. Chambers, Earth Planet. Sci. Lett. 223, 241 (2004). https://doi.org/10.1016/j.epsl.2004.04.031
3. A. Morbidelli, C. R. Geosci. 339, 907 (2007). https://doi.org/10.1016/j.crte.2007.09.001
4. A. E. Ringwood, Geochim. Cosmochim. Acta 30, 41 (1966). https://doi.org/10.1016/0016-7037(66)90090-1
5. J. Li, C. B. Agee, Nature 381, 686 (1996). https://doi.org/10.1038/381686a0
6. B. J. Wood, M. J. Walter, J. Wade, Nature 441, 825 (2006). https://doi.org/10.1038/nature04763
7. J. F. Rudge, T. Kleine, B. Bourdon, Nature Geosci. 3, 439 (2010). https://doi.org/10.1038/ngeo872
8. C. Patterson, Geochim. Cosmochim. Acta 10, 230 (1956). https://doi.org/10.1016/0016-7037(56)90036-9
9. T. Kleine et al., Nature 418, 952 (2002); https://doi.org/10.1038/nature00982
Q. Yin et al., Nature 418, 949 (2002). https://doi.org/10.1038/nature0099510. M. Schönbächler et al., Science 328, 884 (2010). https://doi.org/10.1126/science.1186239
11. D. Porcelli, D. Woolum, P. Cassen, Earth Planet. Sci. Lett. 193, 237 (2001). https://doi.org/10.1016/S0012-821X(01)00493-9
12. R. M. Canup, E. Asphaug, Nature 412, 708 (2001). https://doi.org/10.1038/35089010
13. H. Wänke, T. Gold, Philos. Trans. R. Soc. London A 303, 287 (1981).
14. C. Münker, S. König, T. Schulz, Mineral. Mag. 75, 151 (2011).
15. B. J. Wood, A. N. Halliday, Nature 465, 767 (2010). https://doi.org/10.1038/nature09072
16. F. Albarède, Nature 461, 1227 (2009). https://doi.org/10.1038/nature08477
17. D. Lauretta, Elements 7, 11 (2011). https://doi.org/10.2113/gselements.7.1.11
More about the authors
Bernard Wood is a research professor in the department of Earth sciences at the University of Oxford in the UK.




