Synthesizing molecular fishing nets

A tourist enjoying the sunset at the harbor of a Mediterranean village will likely notice fishing nets spread out on the quay walls for drying. If the observer has a sense for aesthetics of structure, he or she will recognize that the beauty of the nets lies in their regularity and simplicity. Except for where they need mending, the nets consist of knots, or cross-links, connected by rope segments of uniform length, each knot connected to three or four neighbors.

Topologically, such a net is a two-dimensional object. Stretched out flat on the ground, its regularity—or periodicity—is apparent. Gathered up into a compact, 3D state, the periodicity is hidden and the net’s beauty is diminished. Not only that, the net transitions from a more functional state to a less functional one.

Over the past several decades, chemists have been working to realize fishing nets on the molecular scale. Much the way real fishing nets are designed to capture big fish but allow small fish and tadpoles to swim free, molecular fishing nets have potential as selective membranes for gas separation, water desalination, and other applications. Unlike their larger counterparts, the molecular nets can also be tailored to have novel electronic properties and pore functionalities. In the chemists’ terminology, the molecular fishing nets are called 2D polymers. They are a new, organic class of 2D materials.

Flatland chemistry

Two-dimensional materials abound in nature. Important examples are graphene, layered silicates, and molybdenite, all of which formed through diagenesis and metamorphosis while our planet was still young and are not produced by the biosphere. Such materials can be created in a lab, but typically only under harsh conditions that preclude molecular design. The synthesis of graphene, for example, requires chemical vapor deposition at temperatures near 1000 °C. (For more on graphene-like 2D materials, see the article by Pulickel Ajayan, Philip Kim, and Kaustav Banerjee, Physics Today, September 2016, page 38 .)

Chemists realized early on that it would be useful to grow 2D materials in a more controlled manner, under milder conditions. The key ingredients for such synthesis are trifunctional building blocks—branched molecules with three reactive sites.

Such building blocks underlie the recent emergence of 2D covalent organic frameworks (COFs). ¹ The structures of 2D COFs can be widely tuned by changing the trifunctional building blocks, varying the chemical connections between those blocks, and incorporating linear, bifunctional molecules among the branched components. The materials have been intensely explored for their gas-storage, catalytic, and conductive properties.

However, such COFs often are plagued by lattice imperfections. And although their lattice structures have 2D periodicity, they are ultimately 3D macromolecules: The layers are typically stacked and connected by covalent bonds. The molecular fishing nets we discuss here are organic 2D polymers that have long-range regularity and no covalent connections between layers. They are, in the truest sense, two dimensional.

The concept of polymerization is commonly associated with linear molecules. Almost 100 years ago, Hermann Staudinger proposed the existence of long chain molecules composed of covalently bonded repeat units and dubbed them “Makromoleküle.” ² Physical entanglements between macromolecules comprising thousands of repeat units give rise to elasticity, impact resistance, and other properties that have come to be widely associated with polymers. From natural rubber to synthetic polyethylene, polymers have revolutionized our daily life. Practically every commercial product contains a “plastic” component of some form. (See Physics Today, December 2017, page 10 .)

In light of that triumph, it may appear surprising that until recently, apart from a few scattered attempts, ³ there had been no systematic investigation into the feasibility of 2D polymer synthesis. Roald Hoffmann brought that situation to light in 1993 when, in a remarkable article for Scientific American, he took up the cudgels for gaining control over the “wasteland” of 2D (and 3D) organic synthesis. ⁴ It took another 20 years before a team led by one of us (Schlüter) synthesized and structurally characterized the first 2D polymer. ⁵

The key difference between 1D and 2D polymerization boils down to connectivity. As illustrated in figure 1a, linear polymerization requires bifunctional monomers: After one of a monomer’s functional groups collides and bonds with the active end of a growing polymer chain, the monomer’s remaining functional group provides a site at which the next monomer can attach. The lone reaction site at the end of the chain is preserved with each growth event. How the chain end positions itself relative to the rest of the chain does not matter. There are no particular spatial conditions on topologically linear growth; only the efficiency of bond formation matters. That makes synthesis easy.

Figure 1.

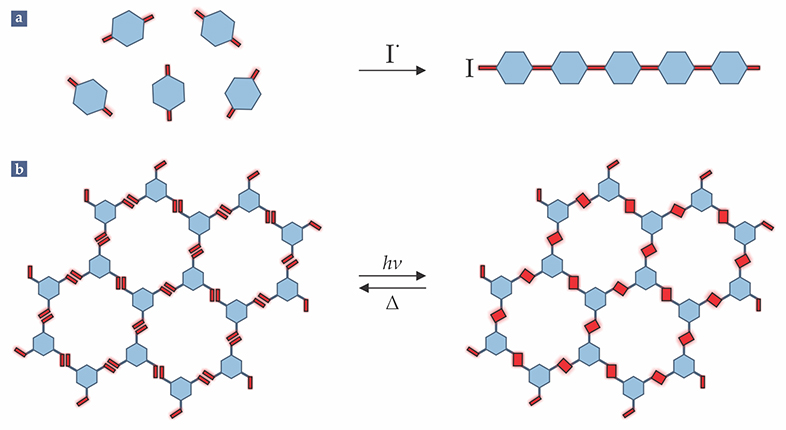
In contrast, 2D polymerization requires monomers that are, at minimum, trifunctional. After an incoming monomer bonds to a reactive site at the edge of a growing sheet, its two remaining functional groups form the sheet’s new edge. However, because bonds can rotate and molecule segments can bend, twist, and stretch, the two functional groups aren’t guaranteed to stay in the sheet’s plane. If the polymer is grown from a homogenous solution, both planar and nonplanar conformations will contribute to growth and the sheet will inevitably depart into the third dimension. The product will be not a sheet-like polymer but an irregular 3D network.

Thus to build a 2D polymer through irreversible chemical bonding, one must not only orchestrate efficient bond formation but also ensure that monomers maintain in-plane orientations. The latter condition is the essential difference between 1D and 2D polymerization, and the difficulty of meeting that condition may explain why 2D polymer science lags so far behind its 1D counterpart.

The “magic” crystals

Currently the most effective way to synthesize 2D polymers is via a two-step process, illustrated in figure 1b. First, monomers are confined to a reactive packing, a 2D crystalline arrangement in which neighboring monomers are positioned with their reactive sites aligned. Then an external stimulus, usually light, induces the sites to covalently bond, transforming the packing into a 2D polymer sheet.

For the reactive-packing step, we focus here on a method that involves coaxing monomers to precipitate from solution into a macroscopic crystalline arrangement. Such packings can contain hundreds of thousands of 2D crystalline sheets that stack noncovalently to form a layered material much the way graphene stacks to form graphite. An alternative approach involves the self-assembly of monomers into a monolayer packing at an air–water interface.

The preparation of monomers in a crystalline state can be orchestrated through careful control and manipulation of intermolecular interactions, including strong ion–dipole and dipole–dipole interactions, hydrogen bonding, and weak van der Waals interactions such as π–π stacking. To gain a measure of control over those interactions, one can vary temperature gradients, solvents, and other crystallization conditions. Or in cases in which the monomer carries a net charge, one can vary the nature of the charge’s counterions. Such manipulations are known collectively as crystal engineering.

Still, the crystallization process can be erratic. Finding the right monomer and the right conditions to produce a suitable reactive packing often takes healthy doses of luck and persistence. But the odds of success can be maximized through systematic screening of crystallization conditions.

An enormous number of chemical bonds must form to create even a micrometer-sized polymer sample, and structural defects cannot be repaired after the fact. So before polymerizing a reactive packing, one typically uses x-ray diffraction to check the quality of the crystalline arrangement. More precisely, one evaluates reciprocal-space reconstructions of hk0 planes, which can be understood as Fourier transforms of the monomers’ projection along the stacking direction of the layers.

Both the shape and size of the Bragg diffraction spots are assessed. Banana-shaped spots indicate mosaicity—the presence of grains of different orientation—and signal that the packing needs to be recrystallized. Fully circular spots signal that the packing is ready for polymerization. High-angle scattering is also desirable, as it indicates greater local order.

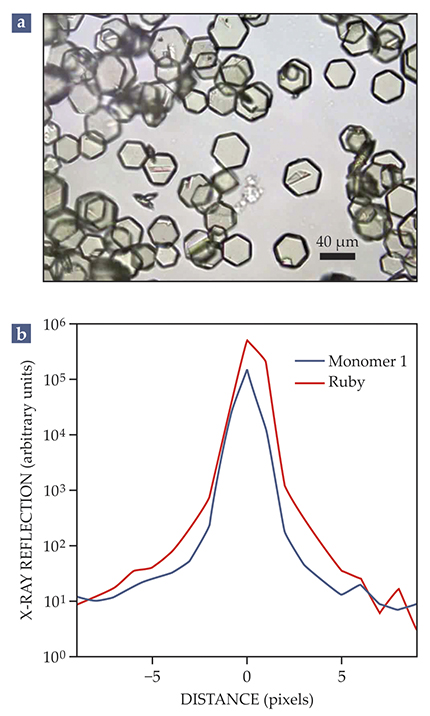
To push the limits of perfection, one will often recrystallize a sample several times, until the full width at half maximum of the Bragg reflections approaches the x-ray source’s resolution limit. Diffraction experiments at a brilliant light source have confirmed that the quality of the monomer crystals can rival that of a ruby reference crystal, as shown in figure 2.

Figure 2.

Two-dimensional polymerization is an incredibly complex synthetic process, and the separation of the reactive-packing and polymerization steps affords an invaluable opportunity to optimize the monomer packing before the trigger is pulled to transform it into a polymer. That those steps are not separated in the synthesis of 2D COFs is likely a cause of the materials’ structural defects.

500 000 bonds per square micrometer

In contrast to the harsh conditions used in chemical vapor deposition, 2D polymerization is typically carried out at or below room temperature, through photochemically triggered dimerization of adjacent reactive groups. ⁶ Typical times for full conversion range from a few minutes to a few hours, considerably longer than, say, the fraction of a second that it takes to form a polystyrene chain via radical polymerization.

Ideally, a near-perfect monomer crystal would polymerize into a stack of equally perfect 2D polymer sheets having the same porous structure and lateral size as the original crystal. However, chemical transformations in crystals are complex, ⁷ mainly due to effects of mosaicity, changes in lattice parameters during chemical conversion, and the complicated relationships between defect formation and bond-formation sequence. That sequence, a priori, is known neither in space nor in time. The more easily a crystal can accommodate local stresses and the less its lattice parameters—particularly the angle parameters—change during polymerization, the more likely that bonds will form evenly throughout the crystal volume. To help accommodate local stress, it is advantageous if the monomers are conformationally flexible. And because any mosaicity in the initial reactive packing tends to be exacerbated as polymerization proceeds, high-quality starting crystals are necessary to ensure sufficient quality of the product crystal.

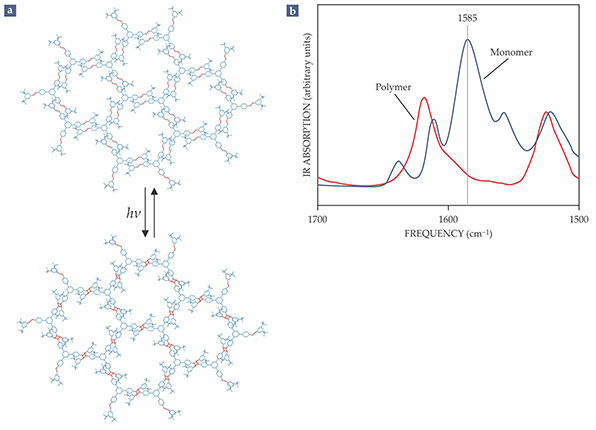
Two of the most rigorously studied molecular building blocks for 2D polymers are organic molecules known simply as monomer 1 and monomer 2. Monomer 1, a propeller-shaped molecule that presents three anthracene units as its functional groups, can be produced with industrial methods. Monomer 2 has three unsaturated, positively charged arms—each with a carbon–carbon double bond as a functional group (see figure 3a)—and is commercially available. Both monomers can be synthesized at reasonable cost in 100 g quantities, more than enough to thoroughly explore the properties of their respective polymers.

Figure 3.

The mechanism of polymerization has been extensively studied for monomer 1, and single-crystal x-ray diffraction monitoring revealed that the bond-formation sequence is nearly random. ⁸ In principle, that bodes well for the structural homogeneity of 2D polymer sheets. However, precise quantitative measurements remain difficult to obtain.

Although high-quality x-ray diffraction can provide unequivocal proof of structural regularity, it is not sensitive enough to confirm whether all of a reactive packing’s functional-group pairs—which for monomer 1 numbers between 500 000 and 1 million in a single, 1 µm² layer—have chemically bonded. Nor are any other existing analytical techniques. The IR spectra (figure 3b) of a reactive packing of monomer 2 and its corresponding 2D polymer illustrate the difficulty. The signal at 1585 cm⁻¹, corresponding to the monomer’s C=C functional groups, is strong in the reactive-packing spectrum but absent from the polymer spectrum, as expected. But the resolution does not allow one to rule out the possibility that a few unreacted C=C groups remain. The synthesis of molecular fishing nets therefore calls for not only new ways to orchestrate the formation of unprecedentedly large numbers of chemical bonds but also new analytical methods to detect them.

Singling out sheets

When 2D polymerization is carried out at an air–water interface, the reaction step yields a single polymer sheet. In the stacked, single-crystal approach, however, the additional step of exfoliation is required to obtain single sheets. The process is nontrivial. Even in wet exfoliation, a relatively gentle process, some sheets may rupture and others may stick together. Quantifying the yield of single sheets from an exfoliated crystal remains a challenge. The lack of yield data makes it difficult to tease out relationships between crystal-structure parameters, growth mechanisms, and product sheet sizes.

Structural analyses of the various 2D polymers reported to date vary significantly in depth and precision. But by and large, polymer sheets obtained from single crystals have been far better characterized than those obtained from polymerization at an air–water interface. The latter is challenging due to the minuscule amounts of material involved, the softness of the monolayer sheets, and the sheets’ sensitivity to electron beams. ^{9 , 10} The small amounts, on the order of micrograms, push many analytical methods to their resolution limit. The softness allows for constant conformational changes, which can render the sheet’s structural regularity undetectable to, for example, grazing incidence x-ray scattering. Because the 2D polymers synthesized to date all have low heat conductivities—considerably lower than graphene’s—they tend to burn away when exposed to an electron beam. Some electron diffraction results have been reported, but high-resolution imaging of a single sheet, which requires a much higher electron dose, remains elusive.

As a result, no sheet synthesized at an air–water interface has ever been unequivocally proven to be a 2D polymer, ¹¹ though one imagines that will soon change. If so, the interface approach may offer a key advantage over its single-crystal counterpart: It can generate monolayer sheets of macroscopic lateral dimensions. In principle, the sheets can be as large as any water surface used to make them.

Handling the invisible

One way to qualitatively check a polymer sheet’s mechanical coherence and robustness is to see if it will stably span the micrometer-sized holes of a transmission electron microscopy grid. In most cases, the single sheets won’t be visible with the naked eye, so one must use either differential interference contrast light microscopy or scanning electron microscopy to confirm that the holes are spanned. It can be particularly instructive to rupture the sheet by firing an electron beam through one of the grid holes. Within seconds, the sheet will roll up at the rupture line, as in figure 4a. The resulting image contrast allows one to confirm the presence of a single monolayer without having to apply spectroscopy.

Figure 4.

In solution, the polymers’ tendency to undergo conformational changes complicates their handling. Stacks of dozens of sheets, such as those in figure 4b, are usually stiff enough to preserve their shape. But as stacks are exfoliated down to single sheets, the polymers eventually undergo a hard-to-soft transition and will begin to change conformations. That breathes life into them.

Applying renormalization theory to the scaling of soft 2D polymers in dilute solution suggests two stable conformations, or fixed points, at which self-similarity and universality prevail: a compact state, which is common to 1D polymers, and a flattened state unique to 2D polymers. ¹¹ In other words, 2D polymers tend to either collapse or fully extend—and then stay that way unless conditions change.

When performing wet-exfoliation experiments, it’s important to be aware of those fixed points. Single sheets in the flattened state have a built-in tendency to aggregate by stacking and precipitate out of solution. One can often prevent that aggregation by manipulating the solution temperature or engineering higher-order interactions between functional groups on the sheet surfaces to coax the sheets into dynamic, slightly crumpled states that avoid the surrounding fixed points.

An experiment with wet-exfoliated single sheets deposited onto a silicon wafer illustrate the importance of the liquid medium. An atomic force microscopy image taken after the sheets were washed with acetone revealed rolled-up edges that weren’t observed before the wash. In the liquid-exfoliation medium, the crumpling was minimal enough that sheets tended to flatten when they absorbed onto the silicon substrate. But the acetone wash partially lifted the sheets from the substrate, whereupon they instantaneously assumed a compact, rolled-up state. Experiments of that sort promise deep insights into sheet dynamics and need to be further developed.

Polymers at work

Synthetic 2D polymer sheets range between approximately 0.8 nm and 2 nm thick, have lateral extensions ranging from micrometer to centimeter length scales, and contain structurally monodisperse pores whose sizes can be tuned from a few nanometers down to subnanometer length scales. Some have conjugated structures, with electrons delocalized along the entire network. All have addressable functional groups at the pore rims and sheet edges.

The polymers can be used as single sheets, in thin stacks of several dozen sheets, or in thick, millimeters-tall stacks of thousands of sheets. The pores in sheet stacks can be filled with guest molecules to create what could be called a nanoblend, whose properties combine those of the network and the guest. (In a single sheet, the guests would fall out immediately.)

All those features lend themselves to a host of potential applications. Single- and few-layer 2D polymers have potential as membranes for nanofiltration, water desalination, and even gas separation. Two-dimensional polymer membranes are thinner and their pores more regular than conventional membranes based on cross-linked linear polymers, and they are much thinner than porous crystalline zeolites. Unprecedentedly high permeances are therefore to be expected.

Plus, because the pores’ sizes can be tuned and have a strictly defined chemical structure at their edges, they can be adjusted to the needs of the application. One can attach functional groups—charged or neutral, polar or nonpolar, large or small—in a structurally defined manner. That flexibility opens the attractive opportunity to use the same kind of 2D polymer for different separation problems. Such variability is unheard of with other 2D materials.

Intentionally introducing pores via perforation techniques, commonly used for graphene-based membranes, is unnecessary with synthetic 2D polymers. The materials also solve the problem of how to make monodisperse holes less than 5 nm in diameter, which has long vexed membrane scientists. Another advantage of 2D polymer membranes is that they are less likely to suffer clogging by contaminants. Clogging by “cake layers”—the particulate deposits that collect on the upstream face of the membrane—remains unavoidable, but the classic problem with conventional membranes, clogging by precipitation inside the pores, is mitigated. Because the membrane is so thin, most contaminants either pass through or are sieved out.

The use of 2D polymers as membranes may also help solve the aforementioned structural-analysis problem of determining whether a monomer crystal has fully polymerized. A higher-than-expected flux through a 2D polymer membrane—especially a nonzero flux of molecules larger than the pore diameter—would indicate the presence of defects.

The potential applications of 2D polymers go beyond membranes and are as diverse as the polymers’ chemical structures. Nonconjugated polymers, which have low conductivity, can be used as nanometer-thin electrically insulating layers. Hexagonal boron nitride, the gold standard of insulating layers, is typically applied in micrometer-sized flakes. But a 2D polymer sheet fabricated at an air–water interface could in principle be used to cover an entire centimeter-sized wafer.

Two-dimensional polymers are also being explored as optical materials for nonlinear frequency conversion. Sheet stacks obtained from monomer 1 are currently being integrated into waveguide devices for frequency doubling and are expected to satisfy the demand for coherent light sources at frequencies that are not accessible with conventional lasers. Such 2D polymer sheet stacks are more easily integrated into devices than are familiar inorganic nonlinear-optics materials such as lithium niobate. Further, because the sheet stacks can exist in two states, monomer and polymer, their nonlinear optical properties can be switched back and forth.

Conjugated 2D polymers, which are expected to have defined electronic bandgaps, are intensively sought after. If obtained, they might develop into the next generation of organic electronic materials. The incorporation of metal centers into such polymers could make them useful in electronic, spintronic, and electrochromic devices and as electrocatalysts for water splitting. In contrast to conventional polymeric films, the spacing between the metal centers, and thus their interactions, could be precisely tuned.

Space to dream

There is an old saying in polymer chemistry that if a new polymer just has a novel enough structure, new properties and new applications will inevitably follow. The field of 2D polymers still has a long way to go before it can rival the societal and industrial relevance of 1D polymers, which are produced at a rate of approximately 300 megatons a year. But the goal isn’t unrealistic.

To anticipate what the future development of 2D polymers will look like, it’s useful to look at the factors that led to the success of linear polymers: the broadening of the structural basis, or range of molecules that can be made; the establishment of analytical methods and theoretical understanding; and the development of processing techniques. Since researchers are just beginning to develop 2D polymers, broadening their structural basis is currently of greatest concern, which is why we conclude this article with a discussion of that topic.

Fewer developments did more to expand the structural basis of 1D polymers than the emergence of copolymers, which combine two kinds of monomers into a single chain. A copolymer’s properties can be efficiently tuned by varying the ratios of the two monomers. Linear copolymers now constitute a billion-dollar market. Copolymerization in the 2D realm could have a similar effect and should be pursued. ^{12 , 13}

For instance, a 2D copolymer would contain at least two kinds of pores, which could be distributed over a sheet’s expanse in different ways—randomly, in alternating fashion, or in blocks, for instance. The different pores could be functionalized to be selectively addressable, so that different external stimuli could trigger their respective opening and closing mechanisms. The flux through such intelligent membranes could thus be regulated with unprecedented selectivity.

Two-dimensional copolymerization could also be used to generate quasicrystalline structures reminiscent of the famous Penrose tiling, illustrated in figure 5a. Such quasicrystalline covalent monolayer sheets don’t exist in nature. In light of the unique properties of 3D quasicrystals, including electrical and thermal conductivities that decrease with decreasing temperature, 2D quasicrystals may harbor additional surprises.

Figure 5.

The broadening of the structural basis of polymer sheets will also involve tuning their molar masses and size. That could be accomplished by using two-laser or masking techniques to selectively irradiate a given volume or area in a reactive packing during the polymerization step. Such approaches will enable investigations of size-dependent properties and open opportunities for customizing the polymers’ shapes.

The search for novel 2D polymers need not be restricted to the realm of classical organic chemistry. Although chemists have fantasized about physically knitting linear polymers into molecular fabrics, ¹⁴ the practical challenges of taming macromolecules in solution may be overwhelming. A simpler approach, inspired by real fishing nets and illustrated conceptually by the image in figure 5b, may be to weave linear polymers, say, on nanoscale “weaving looms,” and then use covalent bonds to fixate the weave at the points where the polymer threads overlay. First steps toward molecular weaving, albeit through crystallization, have recently been reported. ^{15 , 16}

Molecular-scale analogues of origami and kirigami, the Japanese arts of paper folding and cutting, have been explored as ways to craft 2D materials, such as graphene sheets, into 3D objects. ¹⁷ (See Physics Today, January 2015, page 13 .) Two-dimensional polymers, with their precisely positioned and functionalizable pores, add a new layer of possibility. For instance, in a 2D-polymer version of the origami bird shown in figure 5c, the pores on the wings might be functionalized so that they flap up and down with appropriate light triggers. Admittedly, that sounds a bit like science fiction, but without big dreams there can be no big advances.

Such dreams have become undervalued in science. In his 1934 book on aesthetics, Art as Experience, the US philosopher John Dewey wrote, “Indeed, it is safe to say that ‘creative’ conceptions in philosophy and science come only to persons who are relaxed to the point of reverie.” ¹⁸ We could not agree more. Yet scientists are increasingly forced to comply with performance indicators and other irrelevant obligations that leave little space for daydreams. We invested 10 practically publicationless years to develop the first 2D polymer. That few of today’s scientists are afforded the same freedom strikes us as a recipe for stifling creativity and reducing the chances of nonincremental discoveries.