Superfluid helium interferometers

Superfluid helium is a macroscopic quantum system, as are superconductors, gaseous Bose–Einstein condensates, and the interiors of neutron stars. The common feature of those disparate systems is a complex “order parameter” having magnitude and phase. The order parameter can be a Schrödinger-like wavefunction, or it can be some other function that reflects the system’s physical state.

A macroscopic quantum state emerges in a sample of matter when the particles’ thermal de Broglie wavelength approaches the interparticle spacing. The particles then lose their individual identities and merge into a smoothed cloud that behaves as a single correlated quantum state. Matter in such a state differs markedly from a classical collection of distinguishable pointlike particles. For example, the unique quantum properties of superfluid He include zero viscosity, which allows it to flow around a torus indefinitely.

Although superfluid He has been known and studied since 1938, there is still no complete microscopic theory that predicts the transition between normal liquid ⁴He at 2.18 K and the superfluid state at lower temperatures. However, two phenomenological theories explain almost all experiments to date. ¹

The first model, due to Lev Landau, is essentially thermodynamic. It describes the superfluid as a mixture of two interpenetrating components, one normal and one super, each with its own density (ρ_n and ρ_s for the normal and super components, respectively) and its own velocity field (v_n and v_s). The fluid’s total density is the sum of the densities of the two components, and each velocity field is determined independently by its own hydrodynamics. (The motion of the normal component is governed by the Navier–Stokes equation for viscous flow, and the super component in the absence of a temperature gradient is described by the Euler equation for an ideal inviscid fluid.)

A complementary view, provided by Fritz London, Lars Onsager, and Richard Feynman, treats the superfluid as a macroscopic quantum state characterized by a complex wavefunction ψ =∣∣ψ∣e^iϕ. The gradient of the phase factor ϕ is proportional to the superfluid velocity from the Landau model: v_s = (ħ/m)∇ϕ, where m is either the atomic mass (for bosonic ⁴He) or twice the atomic mass (for fermionic ³He). The requirement that the wavefunction be single valued leads to a quantization of fluid circulation.

Many properties of superfluid He have been investigated to date. As illuminating as the studies have been, they have for the most part not led to practical applications in other scientific fields. In this article we describe a new superfluid technology, emerging from work in our groups at Berkeley and Harvard and by others elsewhere, that may prove useful in other fields of investigation. The superfluid He quantum interference device, or SHeQUID, is a quantum phase meter that directly measures shifts in the superfluid wavefunction phase. ² Because external influences affect the quantum phase, the SHeQUID may enable the measurement or discovery of new physical phenomena in fields such as geodesy, seismology, inertial navigation, and gravity research.

Josephson oscillations and quantum whistles

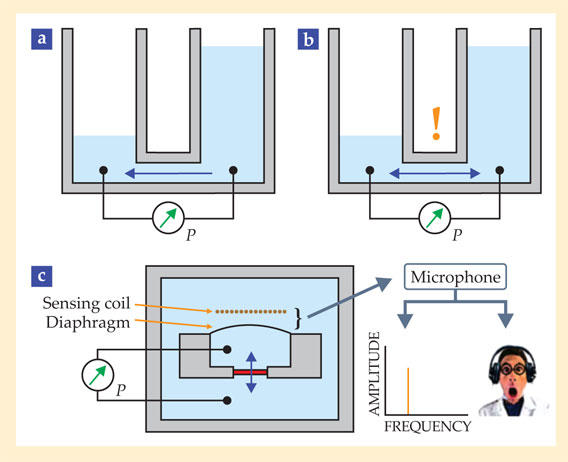
The SHeQUID emerges from one of the most counterintuitive behaviors of superfluids. Consider two fluid-filled tanks connected at the bottom by a small pipe. With a classical fluid, a pressure difference (such as a difference in height) between the tanks causes liquid to flow from one to the other, as shown in figure 1a. But a superfluid—if the connecting pipe is narrow enough and short enough—responds to the pressure drop quite differently: by moving back and forth between the two baths! Applying a larger pressure head in an attempt to force the fluid to flow in one direction results only in an increase in the oscillation frequency. Figure 1b shows the effect schematically.

That bizarre phenomenon, known as the Josephson oscillation, emerges from the two equations that Brian Josephson discovered in the context of superconductors connected by a weak link, such as a layer of nonsuperconducting material thin enough to allow Cooper pairs to tunnel through it. ³ One equation, the Josephson current–phase relation, states that I ∝ sin(Δϕ), where I is the supercurrent flowing between the weakly coupled samples and Δϕ is the phase difference across the weak link. The second equation tells how the phase difference evolves in time due to the presence of a chemical potential difference Δμ—that is, a voltage difference between superconductors or a pressure difference between superfluids:

For a constant Δμ, therefore, the phase difference increases linearly in time and the current oscillates at frequency f = Δμ/h.

Whereas quantum tunneling through a thin wall can suffice as a weak link for superconductors, the He mass is too large to allow appreciable tunneling. To weakly link superfluids, one needs a constricted connection passage whose dimensions are on the order of the superfluid healing length ξ. The healing length is the minimum distance over which the wavefunction can change significantly; superfluidity is suppressed within that distance of a wall. Two superfluid reservoirs joined by a passage of length and width ξ are therefore neither completely disconnected (and independent of each other) nor strongly connected (and virtually a single reservoir). The healing length is temperature dependent and increases near the transition temperature T_λ. It finally diverges; at T_λ itself, superfluidity is suppressed over the entire volume, and ξ diverges. For ⁴He, ξ is typically on the order of angstroms: the size of atoms. A connection passage of that size—an aperture one atom wide in a wall one atom thick—would be too difficult to fabricate and too fragile to handle. However, for ³He, ξ is two orders of magnitude larger. When microfabrication techniques advanced to the scale of tens of nanometers, the study of Josephson physics in superfluids began with ³He.

The first observation of a flow signature consistent with the Josephson current–phase relation came in 1988 from the team of Olivier Avenel and Eric Varoquaux in Saclay, France. ⁴ The Berkeley group observed the Josephson oscillation itself a decade or so later. ^{5 , 6} Figure 1c depicts the apparatus that was used. When fluid oscillates between the two reservoirs, it creates a vibration at an audible frequency—a “quantum whistle” that can be picked up by a pair of inexpensive headphones connected to a sensitive microphone. (For more on using sound for data analysis, see Physics Today, May 2012, page 20 .) The weak link in that experiment was not a single hole but an array of several thousand 100-nm holes. Remarkably, the fluid in all the apertures oscillates synchronously with the same frequency and phase. That coherent behavior may be made possible by the lack of thermal fluctuation in superfluid ³He, only 10⁻³ K above absolute zero.

Interference in quantum fluids

The SHeQUID, shown schematically in figure 2, exploits the quantum whistle discussed above. A torus filled with superfluid He is interrupted by two arrays of apertures that serve as weak links. If a constant pressure difference is applied across the arrays, the fluid in both arrays oscillates at the same frequency with the same phase. The oscillations are coherent not only among the apertures in each array but also between the two macroscopically separated arrays. That coherence is the very essence of a macroscopic quantum system. A microphone coupled to the fluid therefore detects an oscillation amplitude twice as great as that from a single weak link.

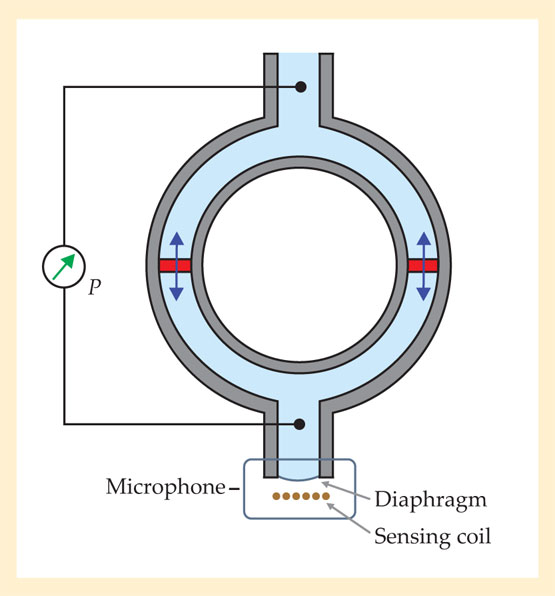
If there exists some phase gradient within the torus, however, the oscillations in the two separated weak links become out of phase by Δϕ_ext ≡ ∮ ∇ϕ · dl, where the line integral is taken over the open torus but not the weak links. The microphone signal’s amplitude, rather than being twice the amplitude at each weak link, is therefore reduced by a factor of ∣cos(Δϕ_ext/2)∣. Thus the SHeQUID becomes an instrument that measures quantum phase differences.

The SHeQUID is a direct analog of a widely used superconducting quantum interference device, the dc-SQUID. ⁷ A dc-SQUID consists of a superconducting loop interrupted by two weak links (tunnel junctions or constriction bridges). A phase shift between the weak links leads to a reduction in the electric current oscillation. Because electrons are charged, the phase shift is caused by changes in the magnetic flux through the loop. A dc-SQUID thus functions as an ultrasensitive magnetometer.

A SHeQUID is an uncharged version of a dc-SQUID. So what is it sensitive to? It turns out that superfluid phase shifts can arise from various physical phenomena, including classical rotational dynamics and quantum effects such as hydrodynamic (as opposed to diffusive) heat flow and quantized vortex motion.

Consider an example of phase shift by rotation. When the torus is rotated at angular speed Ω about an axis perpendicular to its plane, the partitions containing the weak link arrays force the fluid to flow almost as a solid body. Then the fluid velocity in the torus is v_s ≈ ΩR, where R is the radius of the torus. Because phase gradients are proportional to superfluid velocity, the line integral gives Δϕ_ext = (2m/ħ)ΩA, where A is the torus’s area. When the angular velocity vector Ω is oriented at an arbitrary direction with respect to the area vector A, the final product becomes Ω · A.

That phase shift is similar to the Sagnac phase shift ⁸ seen in an optical interferometer when a light beam is split and recombined while enclosing an area A. Physical rotation of the instrument leads to a difference in the path lengths in the two directions that light travels and gives rise to a rotation-induced phase shift proportional to Ω · A. Although the phase shift is small for photons, for He it is more than 10¹⁰ times greater due to the ratio of the mass energy of a He atom (m_Hec²) to the energy of a photon.

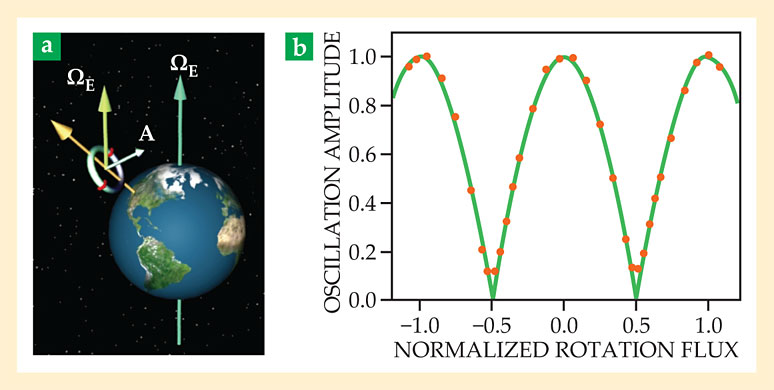
Therefore, SHeQUIDs are promising candidates for ultrasensitive rotation measurements. Figure 3a illustrates the effect for a SHeQUID placed in Earth’s rotating frame. Changing the SHeQUID orientation with respect to Earth’s rotation axis changes the rotation flux Ω · A, which changes the phase difference between the two quantum whistles. Figure 3b shows the interference pattern, observed with a superfluid ³He interferometer. ⁹ Thus a connection between superfluid matter waves and a nonrotating inertial frame leads to a quantum gyroscope that senses absolute rotation with respect to “the fixed stars.”

From helium-3 to helium-4

The larger healing length of ³He made it the natural choice for the first experiments on superfluid Josephson oscillations and interferometry. But ³He atoms are fermions that become superfluid only when they pair up at millikelvin temperatures. A complex and expensive apparatus is required to reach that temperature regime. On the other hand, ⁴He atoms are bosons that become superfluid near 2 K, a temperature that can be achieved much more cheaply and easily. Liquid ⁴He exists at 4 K, and drawing off the hottest atoms with a simple vacuum pump is sufficient to cool it down to about 1.5 K. Because of the angstrom-size healing length, however, observing a quantum whistle in ⁴He seemed to be a daunting task.

But the healing length is a function of temperature. Within 1 mK of the transition temperature T_λ, it approaches 50 nm, a feasible size scale for a nanoaperture array. High-resolution thermometers developed for space missions ¹⁰ allow the system to be maintained at a precisely fixed temperature near T_λ. And so, in 2001, researchers at NASA’s Jet Propulsion Laboratory at Caltech reported hydrodynamic signatures ¹¹ consistent with a sin(Δϕ) current–phase relation in superfluid ⁴He. Josephson oscillations in ⁴He were seen in 2005 by the Berkeley group. ¹²

It turns out that another type of coherent oscillation occurs at the same frequency as the Josephson oscillation, and it allows a ⁴He SHeQUID to operate even at temperatures for which the healing length is much smaller than the aperture size. One of the defining properties of a superfluid is that it flows without dissipation up to some critical velocity. For flow in a channel of micron dimensions, dissipation sets in due to the stochastic formation of quantized vortices. Once a vortex forms on one side of the channel, it moves across the channel by the same mechanism that causes a spinning ball to follow a curved trajectory. As Philip Anderson has shown, a vortex’s traversal of the channel removes a discrete amount of kinetic energy from the fluid flow and causes the phase shift along the channel to drop by 2π. Those discrete 2π phase slips were first observed in 1985 by Avenel and Varoquaux. ¹³

Now imagine applying a constant pressure difference across a channel connecting two superfluid reservoirs. In the strongly coupled regime (a channel much wider than the healing length), the force causes an accelerating flow in one direction. When the flow reaches some critical velocity, it induces a phase slip, and the velocity abruptly decreases. The pressure difference continues to increase the velocity, and the process is repeated. The phase slips take place with an average frequency Δμ/h, identical to the frequency of Josephson oscillations in the weakly coupled regime. Because the phase slips are abrupt, phase-slip oscillations have a sawtooth profile rather than a smooth sinusoidal shape. A continuous transition between the two types of oscillation occurs in the intermediate regime, in which the current–phase relation is neither linear nor purely sinusoidal.

The first observation of coherent phase-slip oscillations was really quite unexpected. Earlier experiments had shown that, due to the stochastic nucleation of the phase slips, superfluid ⁴He in a single aperture in the strongly coupled regime does not actually exhibit such an oscillation. So why should an array of apertures exhibit any phase-slip oscillations at all, let alone coherent ones? But as it turns out, they do, as was discovered serendipitously by Emile Hoskinson of the Berkeley group. ¹² Having constructed a device intended for use with ³He, he first tested it with the less expensive ⁴He. Quantum whistles were audible at temperatures near the transition temperature, but not so near as to allow Josephson oscillations. The whistles were found to be due to phase-slip oscillations, although the mechanisms that remove the stochastic fluctuations and lock the apertures together remain to be understood. To compound the mystery, at lower temperatures further into the strongly coupled regime, the phase slips seem to lose their synchronicity, and the quantum whistle’s amplitude decreases.

Helium-4 interferometers

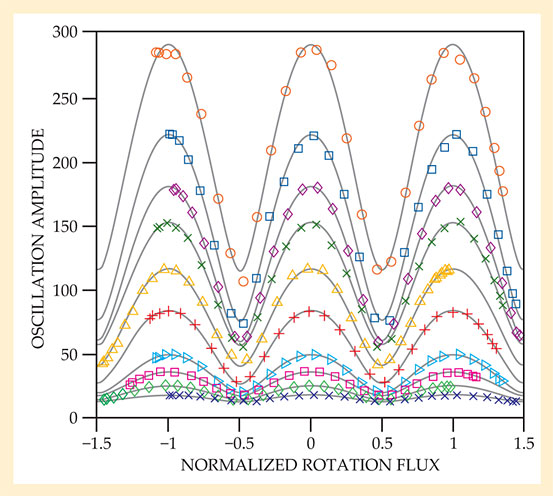
Not only are the ⁴He phase-slip oscillations coherent among the many apertures in an array, they also are coherent between two macroscopically separated arrays, and they exhibit the same phase-dependent interference as Josephson oscillations do. While those behaviors remain a fascinating mystery, they allow a ⁴He SHeQUID to be constructed and operated at temperatures up to 100 mK below T_λ, rather than being restricted to within 1 mK of T_λ. The greater range minimizes the need for precise temperature control; it also allows for greater measurement sensitivity because the mass current to be detected is proportional to the superfluid density, which increases rapidly below T_λ. Figure 4 shows the modulation patterns obtained at several temperatures with a ⁴He SHeQUID configured as a gyroscope. ¹⁴

In addition to proof-of-principle rotation sensing, a ⁴He SHeQUID has also been used to probe some aspects of fundamental physics that had remained elusive in the past. In one such example, a known superfluid velocity was generated by passing a hydrodynamic heat current down a cylindrical pipe, and the phase difference between the pipe’s ends was measured with a ⁴He SHeQUID. ² As a result, the relation v_s = (ħ/m)∇ϕ—the fundamental connection between the superfluid velocity of Landau’s two-fluid model and the phase gradient of the macroscopic wavefunction picture—was quantitatively measured for the first time.

That experiment led to a technological advance that enhances the utility of the SHeQUID. An interferometer of any type typically has a transfer function in which the output amplitude is a cosinusoidally varying function of the variable of interest. The device’s sensitivity then varies with the signal, which can be problematic. However, by including a heat pipe in a SHeQUID interferometer loop, one can inject an arbitrary phase shift to maintain the device at the steepest part of the interferogram even as the external phase shift to be measured varies. The so-called flux-locked SHeQUID, shown in figure 5, can maintain its sensitivity over at least 500 × 2π of external phase variation.

Not surprisingly, a device with a larger area has higher sensitivity. A large-area ⁴He gyroscope with a long, multiturn path was demonstrated in 2011 by the Harvard group. ¹⁵ The total enclosed area is 225 cm², 40 times larger than the sensing area of the first ³He SHeQUID. If combined with recently demonstrated nonlinear amplification techniques, ² superfluid interferometers have the potential to achieve the rotational sensitivity of the best-reported atom interferometers. ¹⁶

Present status and future prospects

The nanoscale aperture arrays at the heart of the SHeQUID technology are now available as commercial products. Displacement transducers ¹⁷ initially developed for gravitational wave detection are used as microphones that detect the mass current oscillations. High-resolution thermometers, originally developed for space missions, provide sub-nanokelvin resolution for exquisite temperature stability near T_λ. A well-designed cryogenic system could maintain the environment at 2 K for many months without the need for any additional liquid He. With those developments, superfluid interferometry may have progressed to a point where one can realistically envision field instruments operating for long periods of time with little need for maintenance or cryogenic expertise.

In their capacity as rotation sensors, SHeQUIDs could complement existing deployed light- and atom-based interferometers in fields such as geodesy, rotational seismology, and inertial navigation. In principle, although not yet in practice, SHeQUIDs could be used to study the effects of a rotating mass on a nearby object: The extremely small general-relativistic effect of frame dragging (or “gravitomagnetism”) is a gravitational analog of a magnetic field arising from a rotating charged object. Frame dragging was recently detected by the Gravity Probe B experiment (see Physics Today, July 2011, page 14 ) and also by some lunar-ranging experiments.

Another tantalizing prospect is to use SHeQUIDs to test concepts related to cosmology. Condensed-matter systems can provide unique cosmological models in the laboratory. ¹⁸ For example, topological defects—features that arise from broken symmetry—exist as dislocations in liquid crystals and as quantum vortices in superfluids. Such defects have been predicted to have formed in the early universe and acted as gravitational seeds for the formation of large-scale structures. Already, SHeQUIDs have been used to detect the motion of single quantized vortices. ² Superfluid interferometry may therefore add a new experimental tool to the field that is mostly observational. Experiments using SQUIDs, conducted by Emil Polturak of the Technion–Israel Institute of Technology and coworkers, have started a trend in the exploration of so-called Kibble–Zurek scenarios of early universe theories. A similar endeavor with a SHeQUID could provide a charge-free environment for experimentation.

Finally, SHeQUIDs may yield new insights about the nature of superfluids themselves. In a superfluid loop, the quantum phase must constantly adjust itself over a macroscopic distance to satisfy the phase-integral condition. Does that adjustment propagate at some finite speed, such as the speed of sound, or is it instantaneous—an example of the “spooky action at a distance” of which Albert Einstein wrote? Or is some combination of the hydrodynamic and quantum pictures required? Can one distinguish the seemingly intertwined concepts of superfluidity, macroscopic long-range order, and entanglement for quantum liquids? The answers to those questions remain to be determined.

Fundamental discoveries in experimental science are often driven by new technologies that emerge from unrelated fields. The development of the diffraction grating led to spectroscopy, which led to quantum physics. Geometric optics enabled otherwise impossible developments in astronomy and microbiology. In this article we have described a developing technology that has emerged from the study of macroscopic quantum effects in superfluids. Two decades ago no one would have expected that superfluids could find application in geodesy to probe variations in Earth’s rotation, yet the application is becoming a feasible reality today. We are just scratching the surface of a new field that can be called applied superfluidity. One might wonder what new discoveries are just around the corner.