Supercontinuum light

The bright, spatially coherent optical radiation emitted by a laser—whether as brief pulses or a continuous beam—can be found in numerous research applications: spectroscopy, photochemistry, communications, atom trapping, nuclear fusion, materials processing, and more. But because the different applications generally demand light in specific regions of the electromagnetic spectrum, engineers have for decades faced the ongoing task of developing new materials that lase at new wavelengths. Fortunately, there’s another, potentially more powerful way to create the new wavelengths—using the processes of nonlinear optics to convert laser light from one wavelength to another. The fiber supercontinuum, a truly remarkable source of optical radiation, has emerged over the past decade out of extensive efforts to master those processes.

A supercontinuum is broadband light generated from the nonlinear frequency conversion of laser light that is focused to high intensity in a dielectric medium. The most useful such light today is produced in optical fiber and typically spans the visible and near-IR regions of the spectrum with up to several watts of average power. Because it is produced in the guided mode of an optical waveguide, the supercontinuum preserves the spatial coherence properties of the incident light and thus essentially combines the brightness and focusing properties of a laser with the bandwidth of a white-light bulb. The result is an essentially arbitrary-wavelength source of spatially coherent laser light. ^{1 , 2}

What makes the supercontinuum so useful is its adaptability. When spectrally filtered, it becomes a narrowband yet tunable source of light. But when used over its full bandwidth, it proves invaluable for such applications as multiwavelength microscopy and the high-capacity encoding of information using multiple data channels that each contain a distinct wavelength. Indeed, a burgeoning commercial market for such supercontinuum sources is growing in imaging and microscopy, where the ability to focus light tightly produces diffraction-limited spatial resolution. Although generating a supercontinuum in the laboratory is easy—it’s simple enough for an undergraduate to carry out—understanding its subtleties isn’t. ³

Immediate impact

An intense laser pulse strongly polarizes a dielectric material such that the induced polarization depends nonlinearly on the electric field of the incident light. That nonlinear light–matter interaction is behind the transformation of the incident narrowband light into broadband radiation. As a rule of thumb, the magnitude of the nonlinear polarization and the supercontinuum bandwidth scale with the pump power, so ultrashort picosecond and femtosecond pulses are usually used as pump sources because they have the highest peak power. But a pulsed source isn’t a strict requirement.

Robert Alfano and Stanley Shapiro generated the first supercontinuum in the late 1960s by focusing picosecond pulses of green laser light into bulk crystals and glasses. ⁴ Researchers conducting subsequent experiments used liquids, gases, optical fiber, and other media. ⁵ But in 1999 Jinendra Ranka, Robert Windeler, and Andrew Stentz revolutionized the field with experiments using a new type of photonic-crystal fiber. ⁶ The fiber’s properties included its ability to confine light to small cross-sectional areas to maintain the light’s intensity over long distances, as well as its engineered dispersion, which was tailored to optimize nonlinear soliton processes, discussed below, that generate a large optical bandwidth. Those advantageous properties, on display in figure 1, enabled Ranka and company to produce a supercontinuum using low-energy sources attainable from common, tabletop femtosecond lasers. Before that development, generating such light required relatively large and complex experimental setups, an obstacle that significantly impeded widespread adoption of the technology.

The experimental simplicity generated enormous interest among the nonlinear-optics researchers who wanted to probe the underlying physics. But it also attracted optical metrologists, who applied the supercontinuum to precision measurements of optical frequencies. ^{7 , 8 , 9} In fact, the supercontinuum was central to the development of the stabilized frequency comb, whose inventors were awarded the 2005 Nobel Prize in Physics (see Physics Today, December 2005, page 19 ). To appreciate the connection between the light source and comb, see the box at right.

Nonlinear and ultrafast

The signature feature of a supercontinuum is continuous spectral broadening in a dielectric medium as light propagates through it. The reason for that broadening isn’t clear at first glance, though, because the familiar processes of optical harmonic generation involve the discrete conversion of one monochromatic frequency to another frequency, say, double or triple the original. ¹⁰ (See the article by Martin Fejer, Physics Today, May 1994, page 25 .) Supercontinuum generation, however, is very different. It depends on how an optical field that already spans quite a broad bandwidth—a short pulse, for example—interacts with a dielectric to generate a continuum of new frequency components. The details fall under the topic of nonlinear ultrafast fiber optics. ³

The linear optical properties of a material are determined by its refractive index. But a short light pulse can experience very large variations in the refractive index as a function of wavelength across its broad bandwidth. Thanks to that dispersion, the different frequency components in the spectrum become out of phase, which broadens the temporal pulse envelope as it propagates down the fiber.

In addition, the power of an ultrashort light pulse can be so high that it modifies the refractive index itself by an amount proportional to the time-dependent incident intensity—a process sometimes referred to as the optical Kerr effect. The nonlinear change in the material’s refractive index in turn generates a time-dependent phase shift in the field oscillations of the light pulse propagating through the material. That self-phase modulation across the temporal pulse generates the new frequency components. Specifically, it creates a temporally changing instantaneous frequency, or chirp, such that the lower frequencies appear on the pulse’s leading edge with rising intensity and the higher frequencies appear on the pulse’s trailing edge with falling intensity, as shown in figure 2.

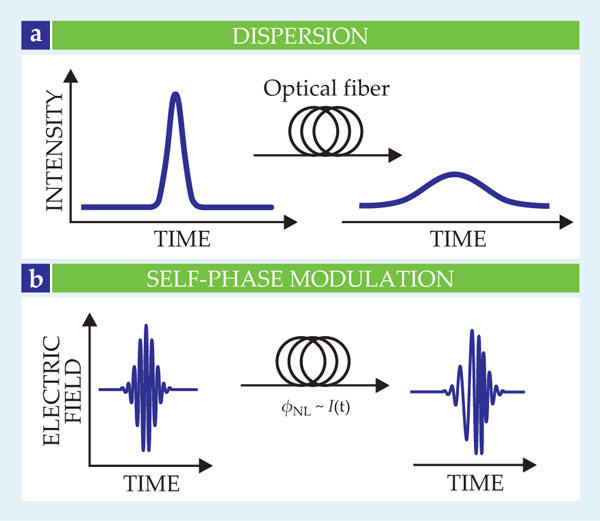
Self-phase modulation occurs when light is focused into any dielectric material, but the effects of diffraction in a bulk medium always limit the distance over which light is intense enough to stimulate nonlinear frequency generation. That explains why optical fiber is such an effective platform for the job: Because light is guided over long distances within a small cross-sectional area, effects such as self-phase modulation can be observed at much lower power in fiber than in bulk materials and can accumulate with propagation distance.

Solitons evolve

Explaining supercontinuum generation in a fiber only in terms of self-phase modulation, however, is an oversimplification. The rich physics of the supercontinuum really arises from the interaction between the nonlinear effect of self-phase modulation and the linear dispersion. The preceding section described how nonlinearity leads to dynamic frequency variations within a pulse envelope, with red-shifted components on the pulse’s leading edge and blue-shifted components on its trailing edge. But depending on the properties of the optical fiber used and the wavelength of light pulses injected into it, dispersion will either increase or decrease the temporal separation between those red and blue components. If it increases, the pulse spreads out in time, but if it decreases, the pulse can stabilize into a waveform known as an optical soliton. ³

Solitons are localized nonlinear structures that have fascinated physicists since their fortuitous discovery on canals in the 19th century, ¹¹ and soliton effects have been identified in a wide range of physical systems, ¹² including optical-fiber waveguides. However, although the most well-known class of optical soliton is the invariant fundamental soliton—essentially, a pulse whose shape and amplitude are unchanging with propagation distance along the fiber—there also exists a class of higher-order solitons. With them, the interactions of self-phase modulation and dispersion produce structures whose shape and spectra evolve periodically with time and distance, as shown in figure 3.

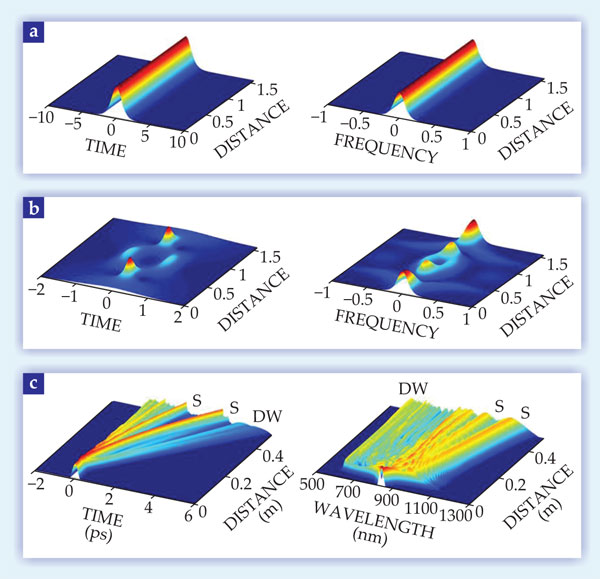
Ideal periodic solitons are essentially impossible to see in practice because even slight perturbations to the fiber’s dispersive and nonlinear responses to light break the symmetry of the evolution. When those symmetry-breaking perturbations occur, the higher-order soliton undergoes a remarkable process known as soliton fission, in which an initial pulse splits into a train of individual fundamental soliton pulses that then undergo further nonlinear and dispersive propagation. Of course, the same perturbations that may induce higher-order soliton breakup can also affect the newly formed fundamental solitons. That fact is key to understanding how the supercontinuum bandwidth increases with propagation in the fiber. For each newly formed soliton, the effect of higher-order dispersion results in a resonant transfer of energy to shorter wavelengths, and the effect of inelastic light scattering within the bandwidth of each soliton leads to a continuous frequency shift to longer wavelengths. ²

Understanding those two processes in full mathematical detail is complicated, but their impact on the pulse breakup in both the time and frequency domains can be readily appreciated from numerical modeling. The left-hand side of figure 3c, for instance, shows soliton fission induced by realistic dispersion and inelastic-scattering perturbations in fiber. The right-hand side shows the spectral evolution of the supercontinuum light, with the frequency-shifted soliton and the dispersive wave generated early in the evolution. The different processes occur such that each injected pulse generates an identical supercontinuum at the fiber output. The optical spectra can span an octave of wavelengths and are extremely stable, with the phase coherence of each pulse preserved over hundreds of terahertz. Thanks to that stability, the octave-spanning supercontinuum revolutionized the field of precision frequency measurement. ^{7 , 8 , 9}

Instabilities

The generation of such a noise-free supercontinuum occurs using pulses shorter than 100 fs. For cases in which longer pulses are used, the initial stage of evolution does not follow higher-order soliton dynamics; instead, a noise-driven process known as modulation instability excites frequency sidebands in the spectrum, leading to strong modulation of the input pulse in time. ³ Remarkably, after that initial growth from noise, the modulated field still evolves to resemble a train of fundamental optical solitons, and one observes the same forms of frequency-shifting dynamics described earlier. ¹³ But because the initial seed is noise-driven, the amplitude and widths of the emerging solitons vary randomly (both temporally and spectrally) from shot to shot, and there is no phase stability with wavelength across the supercontinuum.

A surprising link exists between such supercontinuum noise and the sudden, brief emergence of giant rogue waves on Earth’s oceans (see the Quick Study by Chris Garrett and Johannes Gemmrich in Physics Today, June 2009, page 62 ). ¹⁴ In fact, the propagation of water waves on an ocean and light waves in a fiber have much in common: In both systems, waves are dispersive, and the speed of an ocean wave, like that of an optical pulse, can also depend on its amplitude. In the case of light propagation in a fiber, the noise created by long input pulses can behave like an “optical wind” that triggers the emergence of a small number of short-lived waves, each with extremely large amplitude. The analogy has opened up a new and extremely active field of research that uses optical systems to study nonlinear wave shaping; that research has already confirmed more than 25 years of predictions from the hydrodynamics literature. ¹⁵ It is particularly gratifying to see how rogue-wave experiments in optics are motivating water-tank experiments to generate similar waves in the hydrodynamic environment. ¹⁶ The new research field is also fast developing, since it touches on such issues as turbulence, Bose–Einstein condensation, soft-condensed-matter physics, and nonlinear acoustics.

Applications

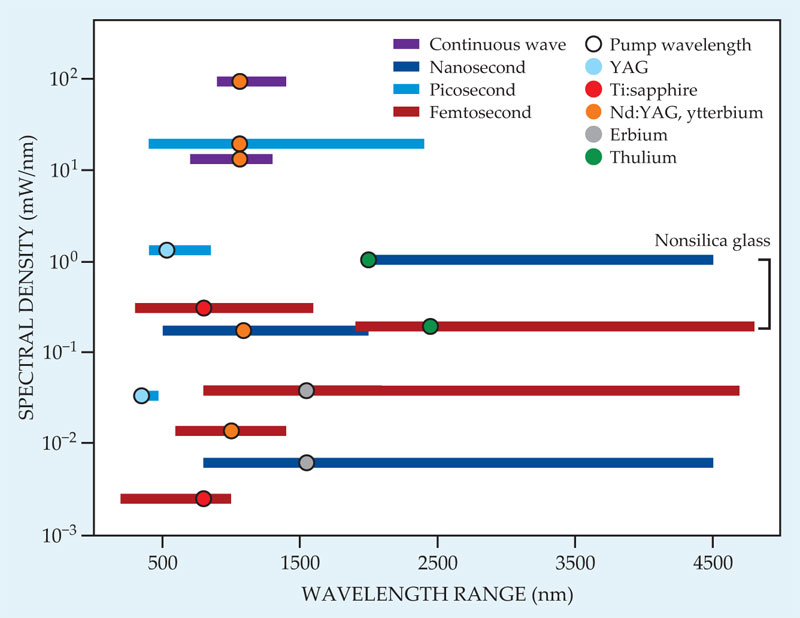
Thanks to the ability nowadays to readily engineer dispersion into optical fibers, it is possible to fabricate optical waveguides that can generate a supercontinuum from a wide range of pump-laser sources. Indeed, laser sources are disparate enough that the coherent radiation available from supercontinuum light spans a remarkably large range itself—from the UV (near 200 nm) to the IR (more than 4 µm). Figure 4 presents a survey of the available sources that use different types of pump lasers, and it shows the spectral power density and bandwidth that each source provides. Virtually any laser source can be used to generate a supercontinuum over some bandwidth range—provided the laser is powerful enough. But only the light generated from femtosecond pulses possesses the high stability required for the most demanding applications in frequency metrology. Nonetheless, even unstable spectra find many applications, such as imaging and spectroscopy, in which time-averaged measurements are important.

It’s hard to overestimate the impact that new developments in optical fibers have on the field. ¹⁷ Before the nonlinearity and dispersion-engineering possibilities of fiber were fully recognized in the 1990s, producing a supercontinuum was an expensive prospect; it took complex lasers and large laboratory facilities. But thanks to advances in fibers and available pump sources, such bright, broadband light is now an affordable, compact technology that’s generally about the size of a shoebox.

Supercontinuum sources are finding commercial success in virtually all areas for which traditional lamps or LED sources had been standard. In confocal microscopy, for example, a broad bandwidth makes it straightforward to filter the output light so that it perfectly matches the excitation wavelength of a fluorophore, the imaging dye in tissue or cells. The sources have also found applications in stimulated-emission-depletion microscopy, ¹⁸ which images at a resolution below the diffraction limit. The technique uses two different wavelengths to essentially inhibit fluorescence in a specific region of the sample and activate fluorescence in a sub-diffraction-limit focal spot within that region. Still other novel applications exist in biomedical diagnostics. As spectroscopic tools, a supercontinuum’s broad bandwidth and local frequency precision make it ideal as an ultrasensitive (parts per billion) probe of, among other things, specific gas-phase molecules in a patient’s breath.

In one of its more surprising applications, frequency-comb technology (outlined in the box on page 31) has improved by as much as two orders of magnitude the stability and accuracy of wavelength calibration in astrophysical spectrographs. ⁹ Such “astro-combs” represent a major advance in the resolution of astrophysical Doppler shifts, a technique for resolving the presence of exoplanets in orbit about a star. The technique is a remarkable example of how fundamental research in one field can find unexpected applications in another.

Brighter future

Supercontinuum generation involves the interaction between a number of different nonlinear effects and the intrinsic linear dispersion of a fiber waveguide. Although its basic physics is now well understood, the richness of the underlying nonlinear dynamics provides ongoing challenges for theory and modeling and continues to offer up surprises.

The ability nowadays to generate such sources with compact tabletop systems has reduced the power needed for nonlinear frequency conversion and has led to new technological developments, commercial successes, and major contributions in numerous fields of science. As new materials and laser-pump sources continue to become available, the supercontinuum can be expected to find new applications, and one can only hope that some of them will be as unexpected and as exciting as the many we have seen to date.

Frequency combs and the supercontinuum

The precise measurement of optical frequencies affects fundamental and applied branches of physics alike. For instance, frequency references are as invaluable to the search for slow changes in the fundamental constants as they are to communications and navigation. To measure an unknown optical frequency, it must be compared with one known more precisely. The technique for doing so was initially developed using room-size frequency chains starting from a stable microwave reference linked to a cesium atomic clock; subsequently, the technique generated precisely known higher frequencies up to the optical regime via a number of intermediate oscillators.

In the late 1990s, however, workers in the field realized that the technique could be greatly simplified using an optical frequency comb generated from a mode-locked laser. The optical spectrum associated with the pulses emitted by a laser whose cavity modes are locked in phase is not continuous. Rather, it consists of a comb of discrete lines, as shown here, exactly separated by the repetition rate at which the pulses are emitted. And that spectral comb can be used as a ruler to bridge a gap between two unknown frequencies under the laser-pulse bandwidth. (See Physics Today, June 2000, page 19 .)

A problem that limits the frequency comb, however, is that the absolute position of comb lines from the laser is generally unknown. However, if the laser is used to generate a supercontinuum that spans an octave in frequency, the position of the lines can be stabilized by reference to an atomic clock through two relatively straightforward RF measurements: one at the pulse repetition frequency 1/T and another derived from the measured interval between the fundamental pulse frequency and its second harmonic. ⁴

The extended bandwidth of the supercontinuum provides much more flexibility in bridging frequency intervals. Around 2000 the use of the supercontinuum to stabilize a comb revolutionized the field of frequency metrology virtually overnight. Frequency combs now enable the measurement of optical frequencies to better than 1 part in 10¹⁵. The precision rivals that of the best atomic clocks. ⁹