Superconducting Magnets Above 20 Tesla
DOI: 10.1063/1.1510280
The primary motivation for developing high-field superconducting magnets is to support scientific research in a variety of disciplines. Because the magnetic field is a thermodynamic variable, it can be used to manipulate phase diagrams of magnetic materials in which the spins of the electrons order ferromagnetically or antiferromagnetically. The quantized orbital motion of electrons in the presence of magnetic fields allows scientists to probe Fermi surfaces, and the quantized electron energy levels associated with fields of order 20 tesla (T) or greater permit access to the quantum and fractional quantum Hall regime. Nuclear magnetic resonance (NMR) techniques, applicable to physical, chemical, and biological systems, have led to a remarkable technology for nondestructive imaging of living systems.
Many investigations require, or at least can benefit from, the homogeneous, low-noise, and temporally stable magnetic fields that can only be achieved with superconducting magnets. Cost and material properties, though, limit the fields that can be produced with superconducting coils. A number of manufacturers now sell 20-T superconducting magnets with bore sizes in the range of 50 mm: Many of those magnets are incorporated into research instruments such as NMR spectrometers or magnetometers. (For comparison, the highest magnetic fields are generated at facilities such as the National High Magnetic Field Laboratory. The NHMFL operates a 45-T “hybrid” superconducting magnet with a resistive insert and also operates 60-T pulsed magnets.) New superconducting materials, including high-temperature (HT) superconductors are enabling the design and construction of solenoidal magnets that have fields approaching 25 T. But achieving 20-T magnets has required many years of work, and as we magnet builders develop magnets that produce stronger fields, we find the cost and difficulty of production growing rapidly. Going beyond 20 T in a superconducting magnet demands long development schedules, large R&D groups, and the application of complex engineering principles. Still, superconducting magnets with ever higher fields are in demand, and efforts to meet that demand continue.
Historical highlights
Soon after Heike Kamerlingh Onnes discovered superconductivity in 1911, he speculated that one could produce a magnetic field of 10 T by means of a modest-sized superconducting coil wound from lead wire. But Onnes never built a 10-T magnet: The inherently low critical fields of the elemental type I superconductors he was using would not allow the impressive fields he imagined. The fundamental limit imposed by those low critical fields prevented the development of superconducting magnet systems until the discovery of type II superconductivity many years later. (For a summary of the evolution of superconducting magnets, see the plot and photographs in figure 1. For a brief tutorial on superconductivity, consult the

Figure 1. Superconducting magnet evolution from the discovery of superconductivity in 1911 to the present. The dramatic progress of the 1960s followed on the ability to fabricate long lengths of high-field superconductor. The 21-tesla nuclear magnetic resonance (NMR) magnet developed in 2001 operates with persistent current, which allows for extraordinarily stable magnetic fields. An important goal being pursued today is to develop a 1 GHz nuclear magnetic spectrometer, which would operate at a field of 23.5 T.
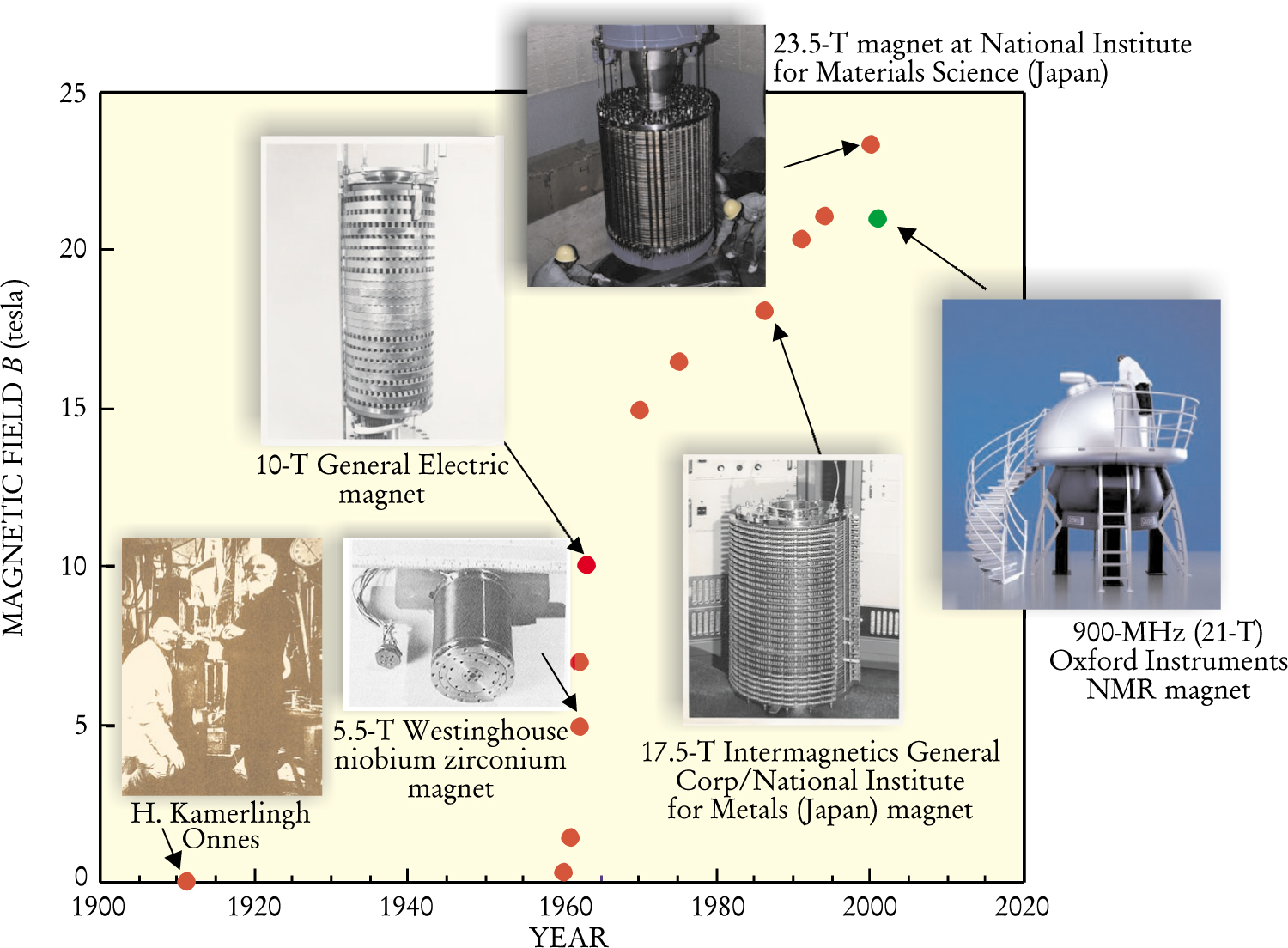
The first successful magnet that used a type II superconductor was built in 1954 by George Yntema of the University of Illinois. The magnet, which used iron pole pieces with niobium (Nb) wire windings, produced a field of 0.7 T. In the course of developing his magnet, Yntema made the important observation that the transport current of his wire depended on the amount of metallurgical cold work introduced into the wire during the drawing process. Thus, unlike the critical temperature and fields—thermodynamic variables that describe the superconducting state—the critical current in a type II superconductor is, to a large extent, a metallurgical variable that depends on processing methods.
In the early 1960s, the discovery by John Kunzler (Bell Telephone Laboratories) of the high superconducting current density in niobium tin (Nb 3Sn) and the almost simultaneous invention by John Hulm (Westinghouse Electric Corp) of a method to produce niobium zirconium (NbZr) wire in long lengths led to a flurry of coil construction activities. By 1963, General Electric Co had produced a Nb 3Sn tape superconducting magnet with a field of greater than 10 T. About a decade later, multifilament Nb 3Sn wire was developed. The multifilament configuration allows for improved magnet stability and increased current densities: Almost all high-field research magnets used today are based on multifilament Nb 3Sn technology.
The discovery of HT superconductivity in 1986 brought about a resurgence in magnet technology. HT superconductors allow for magnets operating well above liquid helium temperature, 4.2 K. But those materials also have very high critical fields, which suggests that they can also be exploited at low temperatures, at least as high-field inserts to Nb 3Sn-based superconducting magnets that operate in liquid helium. Researchers in the US, Europe, and Japan are actively pursuing HT superconductor-insert magnet technology, primarily for application in NMR spectrometers that probe protons with resonance frequencies above 1 GHz (see Physics Today, March 2002, page 30
Superconducting magnet technology
Engineers who design high-field superconducting magnets seek to minimize the volume that contains the magnetic field and also the potential energy stored in the magnet. The reason the volume needs to be minimized is simple: Stored magnetic energy is proportional to the volume that contains the magnetic field, and the cost and difficulty of building a magnet increases with increasing stored energy. The potential energy in a magnet needs to be as low as possible so that the coil can be protected in case the superconductor experiences a transition to the normal state, an event known as a quench.
A superconductor can experience local fluctuations in the temperature or magnetic field. If the superconductor is operating near its critical condition (that is, near the temperature-dependent field that separates the superconducting and normal states), then such fluctuations will lead to a decrease in the superconductor’s critical current. That decrease forces flux motion in the filament, which heats up the filament and further decreases the critical current. If unchecked, this process can lead to thermal runaway and quench. During the runaway, the magnet’s potential energy is deposited as heat into both the coil and the cold structure that is in thermal contact with the magnet. That undesirable event wastes time and liquid helium, and can damage the coil.
To minimize the occurrence of quenches, superconducting magnets use conductors made from a composite of fine superconductor filaments with diameters of the order of microns in a conductive matrix: The matrix, which also aids in the production of long lengths of ductile wire, is usually copper (Cu) for Nb alloys or silver (Ag) in the case of HT superconductors. The increased surface-to-volume ratio of the filamentary superconductor enhances its ability to transfer current and heat to the surrounding conductive matrix in the event of a momentary normalization. The positive-feedback process that can lead to quenches is thus damped, and thermal runaway does not occur. Fine filaments have an additional advantage: They reduce so-called AC losses, flux flow losses due to changing magnetic fields within the superconductor. Such losses are particularly common during charging and discharging, or during the production of a time-varying magnetic field.
The local superconducting-to-normal fluctuations that do lead to quenches must rapidly propagate through the coil and the current should decay quickly enough so that no specific hot spot exceeds a temperature T loc of order 100 K. The maximum decay time τD consistent with this local protection requirement can be expressed as a balance between Joule heating and the thermal content of the coil material:
In the balance formula, J 0 and T 0 are the current density and temperature during magnet operation, δ is the magnetic material density, ρ is the temperature-dependent resistivity of the magnet, and C is the magnet’s heat capacity. Typical decay times are of the order of seconds.
There are a number of methods for enhancing normal current decay and thus preventing hot spots. They include heating the coil to enhance normal zone propagation and inductive coupling to resistive secondary windings. In most high-field magnets, the local protection requirement, rather than the superconductor critical current density, determines the maximum current density allowed.
Superconductivity in brief
Superconductivity exists in about a quarter of all elements, hundreds of metallic alloys, and a group of inorganic compounds whose number is steadily increasing as new members are discovered. The inorganic compounds include the layered ceramics known for their high transition temperature and high critical field. Only a relatively small number of superconductors have been developed for use in high-field magnets, which require long lengths of wire that can be produced in a metallic matrix, electrically insulated, and wound into a coil.
The two varieties of superconductor are called type I and type II. Most elemental superconductors are type I. They conduct current with no resistance and totally exclude magnetic flux as long as they are exposed to fields below a certain critical value H c. When the magnetic field at the surface of a type I superconducting wire exceeds H c, the wire is in the normal state, and current ceases to flow freely. The critical field is a monotonically decreasing function of temperature, and it vanishes at a critical temperature T c. Because H c for type I superconductors is low, those materials are not suitable for high-field magnets. For lead, a representative example, µ 0 H c is 50 millitesla at liquid helium temperature, 4.2 K.
Type II superconductivity occurs in only a few elemental superconductors (niobium being the most notable) but is the dominant form of superconductivity in alloy and ceramic superconductors. Type II superconductors exclude magnetic flux when exposed to fields below a critical value H c1. In the presence of fields above H c1 but below a higher critical value H c2 (see the accompanying figure), these superconductors are in a so-called mixed state, in which circulating currents form “normal” vortex cores pierced by magnetic flux. In an ideal type II superconductor, the vortex cores form a triangular array, called a flux line lattice, maintained by the mutual magnetic repulsion of the circulating currents. When a type II superconductor carries a transport current in a magnetic field, unconstrained flux lines will move under the influence of the Lorenz force. This flux motion creates a resistance to the current and limits the critical current density (loosely speaking, the maximum density sustainable by the superconducting state) in ideal type II superconductors to a relatively low value.

In the type II superconductors used in high-field magnets, the flux lines are pinned by variations in the crystal microstructure. For such superconductors, the critical current density is reached when the Lorenz force exceeds the force pinning the flux lines to the microstructure. Thus, optimizing crystal structure is an important part of achieving high current densities. With optimal structures, type II superconductors can carry significant current densities at fields close to H c2. Niobium tin (Nb 3Sn), a compound used in more than 90% of high-field superconducting magnets, provides an example. For this compound at 4.2 K, H c1 is 20 mT and H c2 is about 24 T. Engineers optimizing the crystal structure of Nb 3Sn have obtained current densities in excess of 100 A/mm2 at 21 T and liquid helium temperature.
The critical current density for a type II superconductor needs to be defined carefully: There is no current density delineating an abrupt transition from superconducting to normal behavior. Note that type II superconductors in the mixed state do not have a resistance that is identically zero. Furthermore the transition, although steep, occurs over a range of current density. It is, after all, associated with the onset of flux motion, and the pinning force varies within the superconductor. Superconductors used in magnets therefore have critical current densities defined according to a criterion such as a specific value for the resistivity, say 10−13 ohm m. In practice, persistent current magnets, which produce very steady fields (decay rates of 10−13/s or less for a total resistance of less than 10−11 ohms), must operate at current densities that are just a fraction of the critical value.
Global protection
When a quench occurs, all the stored magnetic energy is converted to heat in the coil and its cold structure. The combined mass of the coil and its cold structure m must be able to absorb the stored magnetic energy in a manner that will allow the coil to be recooled with liquid helium and recharged. That global protection requirement means the coil cannot be heated above a maximum temperature T max. As with the local protection requirement, T max is determined by energy balance:
The total voltage across a coil during a quench may be just a few volts, but turn-to-turn voltages within the winding can often be substantial—on the order of kV. The higher voltage is possible because, as the current changes during a quench, the inductive and resistive voltages can nearly cancel each other across the coil, but not over a single coil winding. It is crucial that a superconducting magnet have an electrical insulation system that allows the magnet to withstand the high turn-to-turn voltages without damage to the coil. Superconductors for magnets approaching 20 T can present special problems because the superconducting phase is often produced with a heat treatment after the coil is wound. For such superconductors, the insulation system usually consists of a fiberglass braid or cloth that can be impregnated with epoxy to form a solid block winding after the heat treatment is complete. Designers of insulation systems must keep in mind that the systems often occupy a significant fraction of the winding cross section. Thus, insulation can reduce the number of ampere-turns per unit length, a particularly undesirable penalty in the high-field region of the coil.
The conductors within a high-field superconducting magnet are subject to enormous pressures when the magnet is operating. At 20 T, the magnetic pressure is 320 megapascals (3200 atmospheres), enough pressure to cause inelastic deformation in copper. In small bore, moderate-field magnets, the conductor itself can withstand the pressure. But as the magnetic field increases, additional structural material must be incorporated within the winding or on the outside of the coil. Many high-field superconducting magnets are subdivided into multiple nested coils to minimize accumulated stress.
According to the virial theorem, the minimum structural mass is directly proportional to the magnetic energy stored,
Conventional superconducting materials
Quench protection, adequate thermal insulation, and the ability to withstand high pressure are features of all superconducting magnets. So is the availability of long lengths of superconducting wire, frequently in excess of 1 km. Superconducting wires can be fabricated from many different materials, and each has its advantages and disadvantages.
Superconducting magnets that produce fields below about 10 T use filamentary niobium titanium (NbTi) composite conductors. The alloy is ductile, easily fabricated, and relatively inexpensive. The maximum field that can be produced by the composite, as with all superconducting materials, is determined by the critical field H c2. The exact value of µ 0 H C2 NbTi depends on the specific alloy composition: It ranges from 10 to 11 T at 4.2 K and increases to 14–15 T at 0 K.
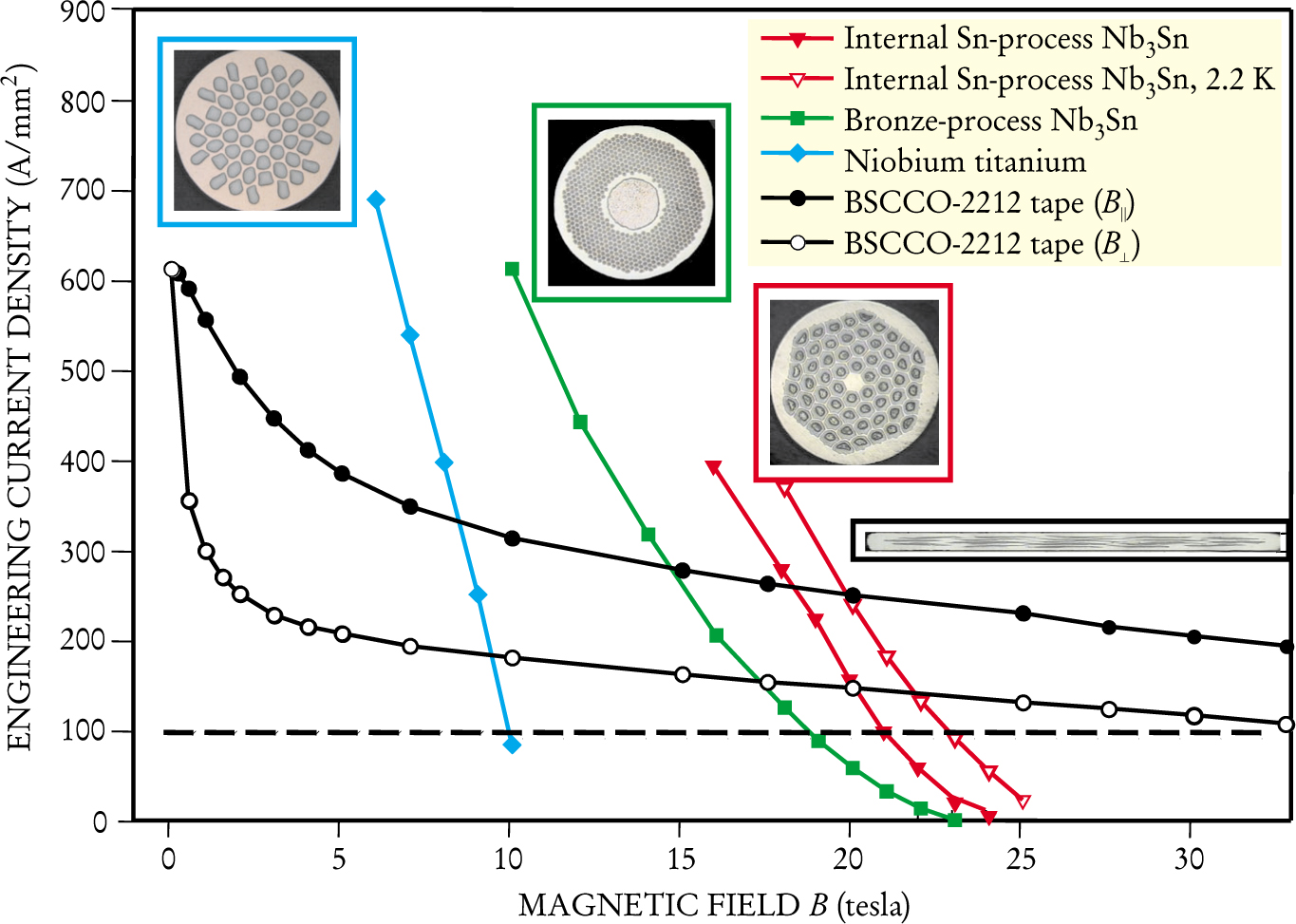
The critical current density J c in a superconductor is another key parameter that determines superconducting magnetic performance. In practice, magnet builders typically refer to the engineering critical current density J E, which is normalized to the composite wire cross section instead of the superconductor cross section. As figure 2 shows, J E decreases with increasing magnetic field. (It also decreases with increasing temperature.) The ampere-turns needed to generate a magnetic field are determined by the superconducting current available, and it is rarely economical to use a particular material at fields in which its J E is less than 100 A/mm2. Figure 2 shows that this economy criterion limits NbTi to magnets with fields below about 10 T at 4.2 K.

Figure 2. Engineering current density J E decreases as the applied magnetic field B increases. The plot shows the falloff for several technologically important superconductors. The dashed line at 100 A/mm2 represents the minimum current density for economically practical magnet development. With the single exception noted in the legend, all measurements are made at 4.2 K. Data are indicated for both internal tin-process and bronze-process niobium tin (Nb3Sn) wires and for fields applied both parallel (B ⊥;) and perpendicular (B ⊥) to ceramic BSCCO-2212 tape. The insets are cross-sectional photographs of multifilament wires and the ceramic tape.
Magnets that generate fields above 10 T require a superconducting material with a higher H c2 than NbTi can offer. In more than 90% of such magnets, that material is filamentary Nb 3Sn composite wire. As discussed earlier, the many filaments provide increased electromagnetic and thermal stability along with reduced AC losses. They also allow for higher overall current densities. Furthermore, lengths of conductor can be connected with superconducting joints, which allows engineers to build persistent current magnets, necessary for applications needing highly stable magnetic fields.
Although Nb 3Sn forms an intermetallic compound with a well-defined crystal structure, the Nb 3Sn composite, depending on just how it is made, can have a range of Sn content. Mechanical processing of the brittle compound is impossible, so composite wire fabrication is done by co-reducing the Nb and Sn as separate components. The most robust large-scale method, the so-called bronze process, incorporates Nb filaments in a bronze (CuSn) matrix. This method, however, limits the Sn content in the composite to about 14% of the bronze by weight. Increasing the Sn fraction, which increases H c2 and J E for a given field, is done by preparing pure or low alloy Sn along with the Nb in a Cu matrix, the so-called internal Sn process. For both methods, the postprocess wire contains no Nb 3Sn: Magnets wound with postprocess wire are heat treated near 1000 K to convert the components to the superconducting Nb 3Sn compound. At 4.2 K, Nb 3Sn can have µ 0 H C2 as high as 25 T. At the same temperature, useful values of J E persist to fields of 19–21 T, depending on the fabrication method.
Both magnet technology (primarily stress control, quench management, and reduced-temperature operation) and conductor development have contributed to the increase in Nb 3Sn magnet field strength from the 10-T levels of the early 1960s to the present state-of-the-art strengths of 22–23 T. For example, figure 2 shows that operating an internal Sn process Nb 3Sn magnet at 2.2 K gains an additional 2 T compared to a 4.2-K operation.
Over the years, J E at high fields has increased steadily in Nb 3Sn compounds, primarily as a result of increased H c2. Incorporating more Sn was one route that enabled the increase of critical field; another was doping the Nb 3Sn layer by alloying either the precursor Nb filaments, the bronze matrix, or the pure Sn filaments. The GLAG (Ginsburg-Landau-Abrikosov-Gorkov) formulation of the BCS (Bardeen-Cooper-Schrieffer) theory shows that H c2 is proportional to both the normal-state resistivity and the critical temperature in the superconductor. Thus, any addition to the Nb 3Sn that increases the resistivity without decreasing T c will push up H c2.
Instead of pure Nb, today’s high-field composites typically use niobium tantalium (NbTa) filaments, titanium additions, or both in the CuSn or Sn. After more than 20 years of effort, it appears that magnet builders working with Nb 3Sn have reached the limit of what they can accomplish with alloying additions and increased Sn content. They are shifting their attention to other materials in their never-ending quest for higher fields.
The ceramic alternative
Ceramic HT superconductors have been developed primarily for applications well above 4.2 K and indeed, a number of low-field magnets currently operate above 20 K. But HT superconducting materials also possess properties that make them candidates for use in high-field magnets that operate at liquid helium temperature. In particular, tapes fabricated from the BSCCO-2212 compound material (Bi2Sr2CaCu2Ox) have a very slow decline in J E with fields well above 20 T, as shown in figure 2. The figure also shows that there is a substantial difference in J E, depending on whether the field is applied parallel or perpendicular to the tape face. Even in the perpendicular orientation, which leads to the smallest J E, the 100 A/mm2 standard occurs above 30 T. That makes BSCCO-2212 a strong candidate for high-field laboratory magnets. Figure 3 displays a coil made with an Ag/BSCCO-2212 conductor that is designed to be inserted as part of a larger magnet. The present world record of 23.5 T for an all-superconducting magnet is held by the Tsukuba Magnet Laboratory at the National Institute for Materials Science in Japan. That magnet contains an innermost BSCCO-2212 coil surrounded by Nb 3Sn and NbTi coils. Inclusion of the BSCCO-2212 coil added 5.4 T to the total field.

Figure 3. High-temperature superconductor coils can be inserted into magnets to boost the generated magnetic field. This coil was developed through a collaboration between Oxford Instruments Superconducting Technology and the National High Magnetic Field Laboratory, and is fabricated using a silver/BSCCO-2212 superconductor, sol-gel insulation, and epoxy impregnation. The coil is wound with more than a kilometer of conductor and has boosted a background 19-tesla field by an additional 3 tesla.

The BSCCO materials (there are useful compounds other than the 2212 formula) are generally fabricated as tapes because these materials have a significant anisotropy in crystal structure and transport properties. The large aspect ratio typically used for the tapes makes magnet engineering difficult. Round wire BSCCO-2212 was fabricated as early as 1989, but until about two years ago its J E was substantially lower than that in tapes. Engineers continue to work toward further improving round wire BSCCO-2212.
A serious challenge—much more so for HT superconducting materials than for low-temperature ones—is understanding and controlling dissipation mechanisms such as flux motion. Dissipation control is crucial for persistent current magnets used, for example, in NMR spectroscopy. An additional challenge is to develop persistent current joints for HT superconducting materials that will allow very steady fields. At present, joints in these materials are not up to NMR standards.
To address problems of anisotropy, dissipation control, and joint technology, magnet builders are considering alternate high-field superconductors such as niobium aluminum (Nb 3 Al) and tantalium tin (Ta 3Sn). Both materials have intrinsically higher values of H c2 than Nb 3Sn. Both, however, have been difficult to fabricate in the long, consistent lengths required for magnet applications.
Science applications
The majority of high-field superconducting magnets are produced for high-frequency NMR spectrometers. In addition to NMR, high-field superconducting magnets are also used in ion cyclotron resonance (ICR), electron magnetic resonance (EMR), and ultralow-temperature physics experiments.
NMR spectroscopy is a very active field of research, particularly in chemistry and biology with their stringent requirements for field homogeneity and temporal stability. High magnetic fields offer numerous advantages, including improved spectral sensitivity and resolution. In many applications, increasing the magnetic field yields multiple benefits; a small boost in field strength leads to a significant improvement in capability.
The spectroscopy of aligned samples of membrane proteins is one such application. Spectroscopists who use high fields enjoy the standard (and significant) improvements in resolution and sensitivity achieved with such fields. But an increase in field strength also increases relaxation times, which leads to sharper peaks for the associated resonance transitions. Moreover, higher fields enhance a sample’s alignment, which further reduces linewidth. Because of the improved alignment, one can use fewer glass plates in preparing a sample and get more sample exposed to the magnetic field. A larger sample, better alignment, and increased relaxation times lead to a multiplicative improvement in NMR performance with field strength.
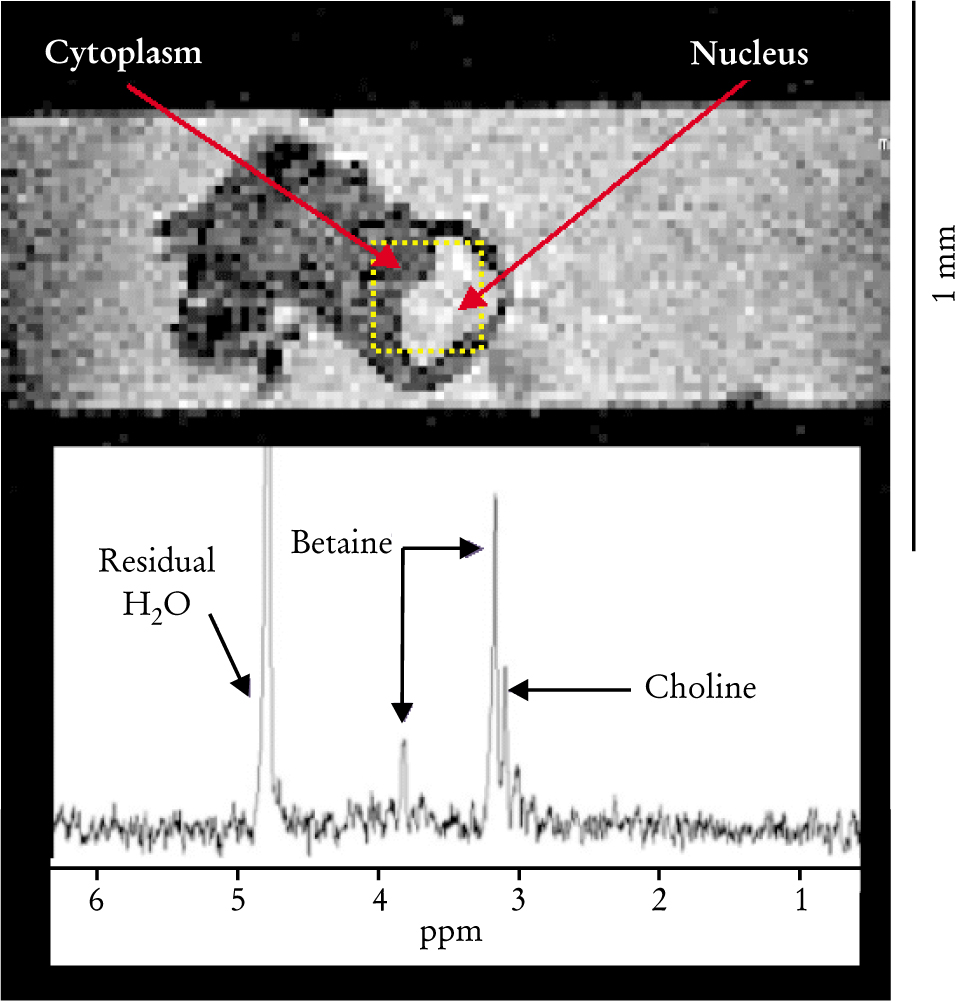
NMR imaging at fields of around 1 T is a routine medical diagnostic. At higher fields, NMR imaging can give extraordinary images of microorganisms and other microstructures. Figure 4, for example, shows an NMR image of a single neuron, along with an accompanying hydrogen spectrum. The ability to obtain such single-cell NMR images is a recent development, possible only with high-field, high-frequency NMR instruments.
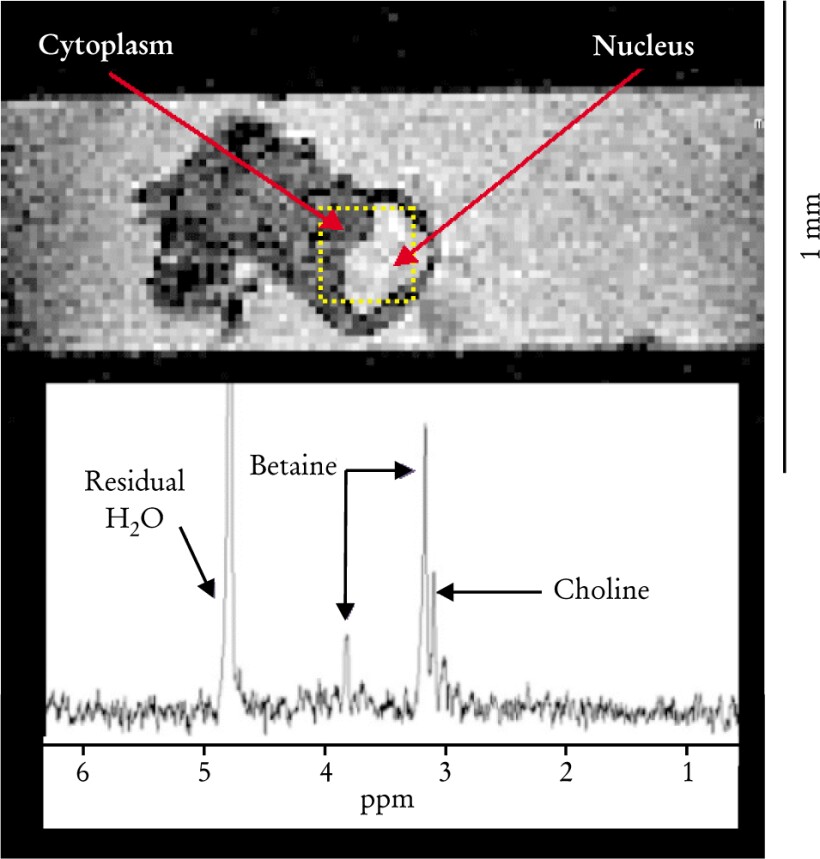
Figure 4. A single neuron isolated from the abdominal ganglion of the sea hare Aplysia californica. The neuron was imaged at 17.6 tesla, corresponding to a proton resonance frequency of 750 MHz. Such images can be used to define a region (here, the yellow box) for localized proton spectroscopy. The hydrogen spectrum accompanying the neuron image displays resonance peaks for the cell’s principal intracellular metabolites. The high magnetic field, in addition to narrowing the spectral linewidths, allows images and spectra to be obtained reasonably quickly. The image of the neuron was acquired in 20 minutes, and the spectrum was obtained from a 15.6-nanoliter sample in 25 minutes.
(Courtesy of Samuel Grant and Steve Blackband, U. of Florida, Gainesville.)
More about the authors
Steve Van Sciver is director of magnet science and technology at the National High Magnetic Field Laboratory in Tallahassee, Florida.
Ken Marken is a staff scientist at Oxford Instruments Superconducting Technology in Carteret, New Jersey.
Steven W. Van Sciver, 1 National High Magnetic Field Laboratory, Tallahassee, Florida, US .
Kenneth R. Marken, 2 Oxford Instruments Superconducting Technology, Carteret, New Jersey, US .




