Strange interfacial molecular dynamics

Biological functions such as gene regulation and metabolism in living cells rely on highly specific molecular interactions. The structure and dynamics of interfaces—from the nanoscale surfaces of intramolecular domains and the molecular surfaces of proteins, to the mesoscale surfaces of organelles, and even to the microscale surfaces of live cells—mediate those interactions. Our understanding of how interfaces evolve and how they couple to their complex environments is still developing, and several Nobel Prize–winning technologies have aided the endeavor to understand them (see box 1).

Here we discuss three examples of interfacial molecular dynamics: the distance fluctuations between the interfaces of internal protein domains, the coupling of proteins and lipid membranes to their surroundings, and the dynamics within lipid membranes—the thin layer separating a biological cell or an organelle from its surroundings. Even though the protein and membrane systems are highly dissimilar, their dynamics share many common fingerprints. Experiments and simulations demonstrate that both systems display rich and counterintuitive dynamics with strong deviations from researchers’ expectations. Experimental evidence has shown that interfacial dynamics in biological systems involve memory effects, which in turn affect molecular biological function in ways that are still not well understood.

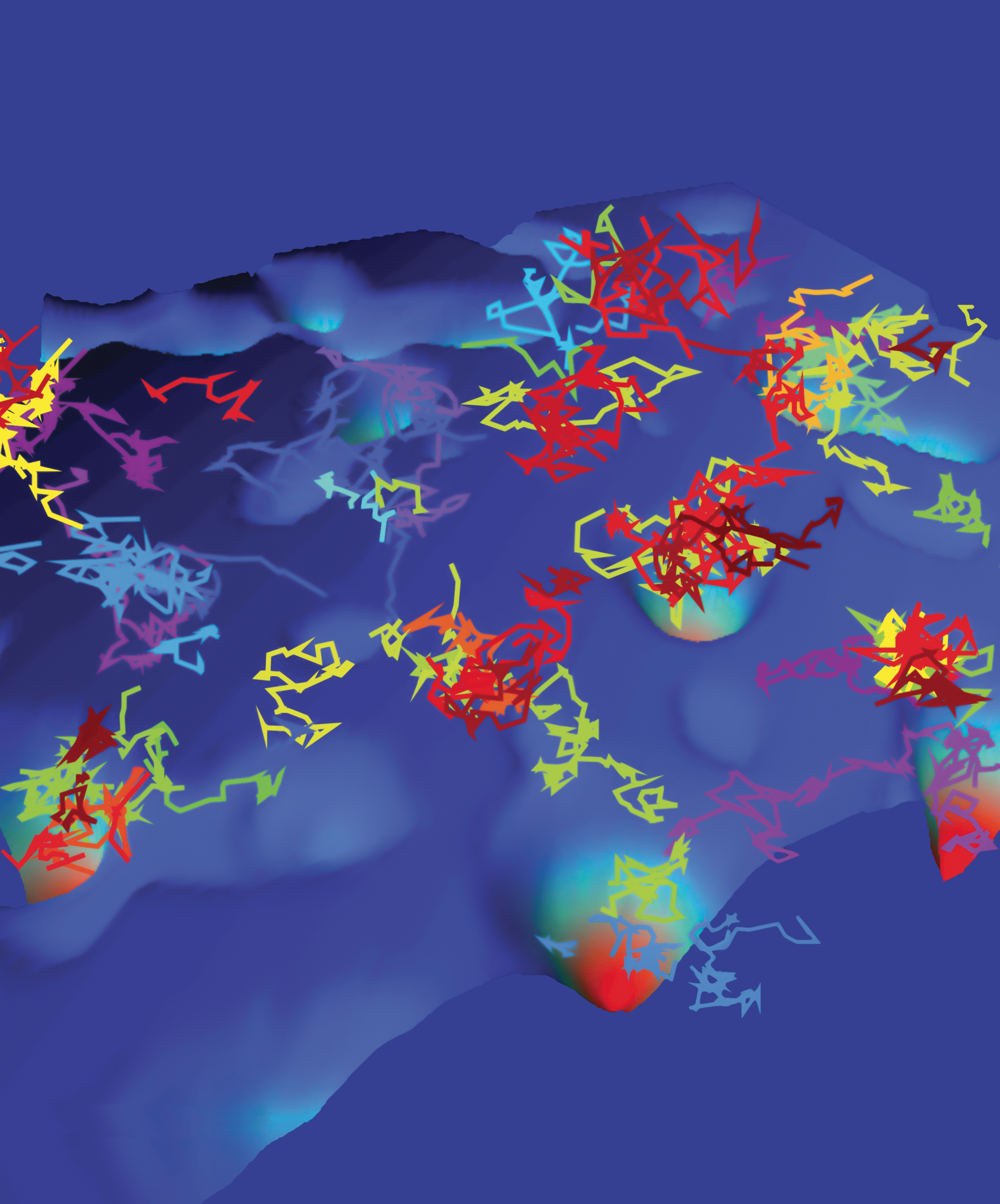
Figure 5.

Until a few years ago, biological interfaces were studied primarily in terms of their chemical compositions and structures. It is becoming increasingly clear, however, that interfacial dynamics also are critical to the function of living organisms. They mediate processes such as the folding and internal dynamics of proteins, the formation of molecular complexes that can require multiple collision events to trigger specific binding, and the highly selective passage of molecules across membranes. Molecules in the water layer around large proteins and membranes not only associate locally with charge groups on individual amino acids in proteins and lipid membrane molecules; they also affect longer-range stabilization by forming so-called molecular water bridges. Water molecules mediate interactions between protein domains and membrane lipids through those bridges and establish a transient network that contributes to the stability of protein and membrane architectures. Molecular water bridges thereby affect the fluctuations in the structures of proteins and membranes and, in turn, influence the efficiency of biomolecular reactions.

Single particle paths

Membranes and molecules at interfaces are continuously bombarded by other small molecules and larger complexes in the surrounding aqueous environment. Thus, one may expect the dynamics of interfacial molecules to be dominated by diffusion as described in the theoretical works of Albert Einstein ¹ and Marian Smoluchowski. ² Within their framework, molecules are always jittering around randomly, completely independent of their pasts. Even for simple uncorrelated Brownian motion in which the mean squared displacement (MSD) is given by $〈\Delta {\mathrm{r}}^2\left(t\right)〉\sim t$, a striking observation can be made: The path of a single diffusing molecule completely covers a two-dimensional surface, so it makes more sense to talk about the area rather than the distance covered by such a random walk. Indeed, in attempts to measure path length with increasingly better resolution, the length increases as a power-law until it reaches the scale of the molecular free path. That increase is similar to the fractal effect that unfolds in trying to measure a coastline: Its length grows longer as the scale of measurement gets smaller ³ (see box 2). Fractality in the path or time coordinate of a random process is a common feature in molecular interfacial dynamics.

For hundreds of years, physicists have been studying the motion of individual particles to understand the physics of large systems. Their basic premise is that observed macroscopic properties arise at the most fundamental level from the dynamics and interactions of the individual components. To make sense of matter’s behavior, one should probe the physics of its constituent parts—atoms and molecules. Single-particle tracking has a long tradition that originated with Jean Perrin’s careful protocols, and what appeared to be science fiction not long ago is now routinely practiced: Careful experiments based on fluorescent tagging allow researchers to follow the motion of individual molecules in living biological cells. ⁴ Today, researchers can measure the locations of individual molecules with nanometer precision while following their motion with millisecond temporal resolution. The gap between the accessible time scales of simulations and experiments is continuously narrowing, and a significant overlap between simulated and experimentally measured dynamics is already possible.

Protein reconfiguration

Proteins—polymers composed of amino acid monomers with specific monomer–monomer interactions—are responsible for most of the essential processes in a living cell, including signaling, active transport, cellular metabolism, and modification of other proteins. A protein’s transition from one conformation to another takes place in the heterogeneous energy landscape of the protein’s highly dimensional phase space.

To function, most proteins in solution first fold into a predetermined structure. Once folded, they typically undergo major conformational changes. Transitions between different configurations are dominated by many small, local conformational changes that add up to a larger protein reconfiguration. The protein crosses a hierarchy of energy barriers but also encounters geometric hindrance, which is often neglected in models. A stark indication of the complexity of protein dynamics was shown in experiments by Hans Frauenfelder at the University of Illinois at Urbana-Champaign in the 1970s. They revealed that the distribution of binding times for ligands showed a power-law scaling over several decades in time. However, at the time it was not possible to tell whether the dynamics were a heterogeneous ensemble effect or due to an individual molecule.

In 2003 Sunney Xie’s group at Harvard University used fluorescent imaging methods in single-molecule experiments; their work showed that internal conformation fluctuations take place on a strikingly large range of time scales, from hundreds of microseconds to seconds. The picture that emerged is one of conformational states with a broad power-law distribution of trapping times, or fractal time. Because of that distribution of trapping times, the distance $\mathrm{R}(t)$ between two protein sites exhibits anomalous diffusion. ⁵

The single-molecule experiments were recently put into a broader perspective in a supercomputing study. Jeremy Smith’s group at Oak Ridge National Laboratory confirmed that $\mathrm{R}(t)$ for the amino acids in a protein, illustrated in figure 1a, shows a power-law distribution of trapping times in specific configurations. Moreover, the dynamics are seen to be nonstationary, or to age, down to picosecond time scales: The characteristic time of the interdomain distance autocorrelation function explicitly depends on the measurement time over seven decades in time. ⁶ Observables in ageing processes depend on how much time has lapsed since the system was initiated. Combining Smith’s results with Xie’s experiment accounts for ageing dynamics in a single protein over a mind-boggling 13 decades in time.

Figure 1.

A paradigm shift is now under way in understanding protein dynamics, and the effects of the interfacial fluctuations can no longer be neglected. Those effects are likely at the core of protein conformational changes and function. To gain mechanistic insight into the emergence of complex organization in proteins, it is essential to probe their dynamics at the protein–water interface, which can dramatically alter intramolecular interactions.

Liang Hong’s group at Shanghai Jiao Tong University provided one piece of evidence for strange dynamics at the protein–water interface through neutron scattering experiments of proteins hydrated by approximately a single water layer. The experiments were performed in tandem with molecular dynamics (MD) simulations. ⁷ The researchers demonstrated that the water molecules on the surfaces of two proteins—cytochrome P450 and green fluorescent protein—exhibit subdiffusion: They both had MSDs of the form $〈\Delta {\mathrm{r}}^2\left(t\right)〉\sim t^{\alpha }$ with an anomalous diffusion exponent $\alpha \approx 0.80$ over times ranging from 10 picoseconds to 1 nanosecond.

The MD simulations showed a gradual change from subdiffusion to nearly normal diffusion $\left(\alpha \approx 1\right)$ at 0.1 microseconds. The researchers interpreted the motion of the water molecules as a random walk with isolated, uncorrelated jump events between small cages, as shown in figure 1b. The jumps are interspersed with scale-free waiting times, and therefore, the process is ageing. Mediated by molecular water bridges, single arrested water molecules influence the larger region around themselves and thus affect the surface dynamics of the entire protein. The full consequences of those effects on protein function remain unknown.

What would cause the fractal immobilization times observed for internal and external protein interface dynamics? In the 1970s Harvey Scher at Xerox and Elliott Montroll at the University of Rochester showed that such scale-free dynamics may readily emerge from energetic traps with random depths (see box 3). The escape times are interspersed with waiting times, $\tau \sim \exp \left[-E_{\mathrm{a}}/k_{\mathrm{B}}T\right]$, where $E_{\mathrm{a}}$ is the energy depth of the well and $k_{\mathrm{B}}T$ is the thermal energy. When the energy depths are exponentially distributed and the temperature is below a critical value, the trapping times have a power law tail with infinite mean (see the article by Harvey Scher, Michael Shlesinger, and John Bendler, Physics Today, January 1991, page 26 ). Given the highly complex nature of a protein surface, it is not surprising that its binding pockets have a heterogeneous distribution of trapping energies. The striking effects of such power-law distributed waiting times have been observed in several biological interfaces. They may be caused by specific attractive interactions, but topological hindrance may also come into play when a protein segment at one area in space impedes the passage of another segment.

Probing single molecules in their natural habitat is crucial to understanding their dynamics and function. When solvated in water, proteins perform extravagantly choreographed ballet dances that often include major displacements of subunits around hinge-like bonds. In addition to that motion, the liquid inside a cell is crowded with large, squishy biomolecules that are incessantly colliding like bumper cars. Over time scales of collisions between the large crowding molecules in the cellular environment, proteins trapped in certain conformations or surface water molecules immobilized for long times might be unlocked by nearby colliding molecules, which would lead to a renewal of the motion: The molecules could resume their vivid choreography and restart the ageing process. That picture is still speculative, but we expect the internal protein dynamics and the motion of the surface water to still be anomalous at least below typical renewal times.

In and around membranes

The same interfacial dynamics that affect single proteins are also important for lipid bilayer membranes that form the surfaces of cells and organelles. First consider the simplest model system for a biological membrane: a self-assembled bilayer of lipid molecules of identical chemistry (figure 2a). Biological lipids typically have a hydrophilic head group and a hydrophobic tail, so in aqueous environments they form bilayers with their tails pointing inward and their heads at the interface with the water. For waiting times shorter than 10 nanoseconds, each lipid’s center of mass shows anomalous diffusion with an exponent $\alpha \approx 0.66$. Gerald Schneider at Louisiana State University and coworkers recently reported an even more marked subdiffusive regime below the nanosecond range in neutron-spin-echo experiments. ⁸ They found an exponent of $\alpha \approx 0.26$ corresponding to short-range motion comparable to the size of a lipid head group. Beyond 10 nanoseconds, most studies indicate a crossover to normal diffusion $\left(\alpha =1\right)$ in both experiments and all-atom simulations.

Figure 2.

When cholesterol molecules—a type of lipid essential for the structural identity of animal cell membranes but better known for causing cardiovascular diseases—are added to the bilayer, they settle snugly between the tail groups of the bilayer lipids. As shown by Ilpo Vattulainen’s group at the University of Helsinki, cholesterols decrease the accessible degrees of freedom of the membrane lipids. That restriction causes a more ordered bilayer structure and, because the lipid tails become more elongated, an increased membrane width (figure 2b). The short-time anomalous diffusion does not substantially change, but for some lipid chemistries, researchers have observed extended anomalous diffusion ⁹ beyond 10 ns with an exponent $\alpha \approx 0.8$.

The correlation between higher membrane disorder and longer-lasting anomalous diffusion is corroborated when proteins are added to the bilayer. Lipid bilayers in biological membranes comprise various lipids with different chemistries, and they are studded with membrane proteins much larger than the surrounding lipids (figure 3). Many of those proteins are tasked with gating specific molecules such as water, ions, proteins, or fragments of genetic code across the membranes; others act as chemical sensors. Experiments have recently shown that protein crowding in single-chemistry, lipid-bilayer model membranes causes persistent anomalous diffusion to at least tens to hundreds of nanoseconds. Interestingly, in crowded membranes the diffusion may no longer have Gaussian step sizes as in noncrowded membranes, and individual lipid and protein motions show intermittent mobilities that alternate between states with largely different diffusion coefficients. ¹⁰

Figure 3.

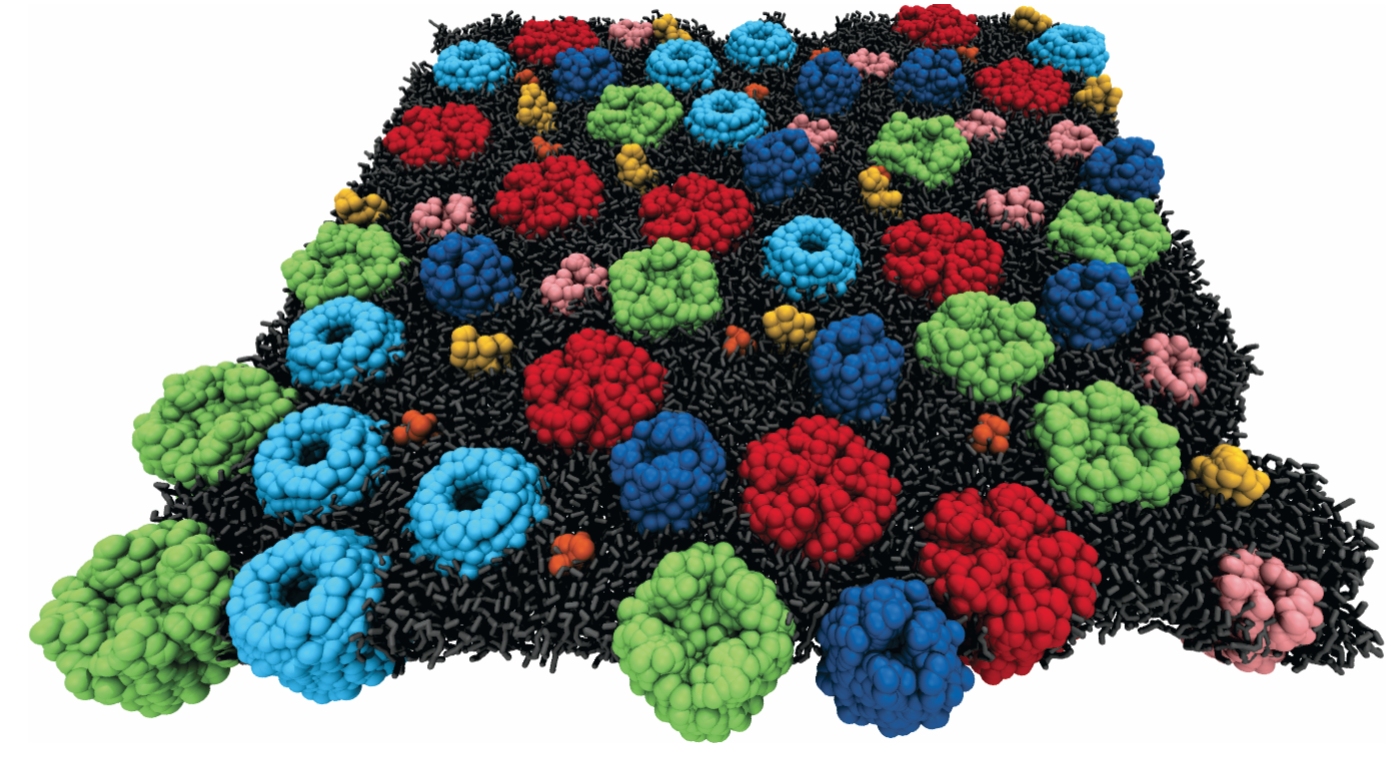
The lipids and proteins in bilayers interact both with each other and with their surroundings. To see the effects of those interactions, Eiji Yamamoto and colleagues at Keio University in Tokyo studied the motion of water molecules and proteins at the water–membrane interface. Their all-atom MD simulations showed that water molecules within 3.5 Å of the lipids are subdiffusive with $\alpha \approx 0.6$ on time scales from 1 to 1000 ps. The simulations revealed signatures of both scale-free immobilization time distributions and antipersistent motion or a negative velocity autocorrelation function. Whereas the antipersistent component has stationary displacements, the scale-free time distributions lead to ageing dynamics of the surface water and the water mobility decreases with time. The time-dependent slowdown may increase the probability that water molecules dock at energetically favorable locations and stabilize the membrane by forming bridges between lipids. Roland Netz’s group at the Free University of Berlin mimicked the jump-like and heterogeneous surface water motion on membranes by replacing the complex environment with a corrugated free-energy landscape, shown in figure 1c, that models the landscape created by the surface head groups of membrane lipids. ¹¹

Going one step further, Yamamoto and others have studied the surface motion of a protein that specifically binds to lipid head groups in multiscale MD simulations. ¹² The results again reveal anomalous heterogeneities in the protein’s diffusion with intermittent localization patterns characterized by an exponent $\alpha \approx 0.5$ from the subpicosecond range to around 10 nanoseconds. At that point the proteins cross over to normal diffusion with $\alpha \approx 1.0$. Both membrane-associated water and proteins exhibit similar anomalous dynamics, albeit with different effective diffusivities.

How do those observations translate into observations of membrane dynamics in complex living cells? Different experimental studies reveal two crucial factors. Due to the increased complexity of the study cases described above, subdiffusion of membrane proteins may reach longer macroscopic time scales of hundreds of seconds, and their motion can be strongly influenced by interactions with the intracellular scaffolds of semiflexible polymers that support the membrane. Scale-free trapping times cause membrane proteins to exhibit ageing dynamics on similarly long time scales. ¹³

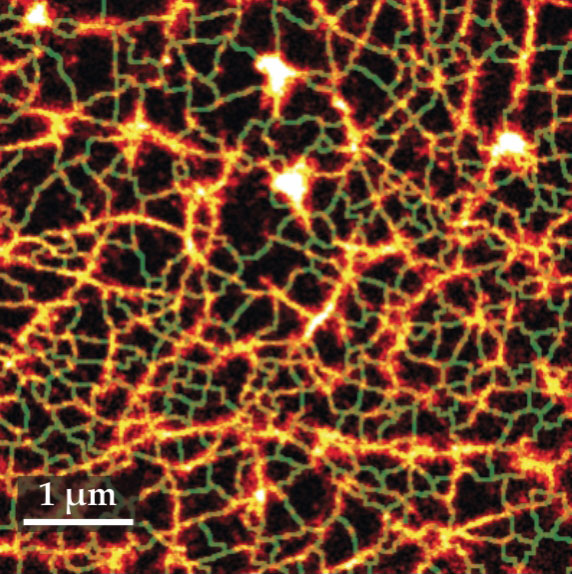
Using a combination of single-particle tracking and superresolution imaging in live cells, researchers found that the actin cytoskeleton that lies underneath the membrane forms a scale-free landscape, shown in figure 4, that causes the ageing protein dynamics to evolve on a fractal substrate. ¹⁴ By using interferometric scattering to track tagged membrane proteins, Philipp Kukura’s group at Oxford University reported similar results describing membrane protein subdiffusion in living neurons that have membrane compartments in the cytoskeleton. ¹⁵ Simulations of a two-component lipid bilayer membrane by Petra Schwille’s group at the Technical University of Dresden showed even more pronounced subdiffusion due to coupling to cytoskeletal scaffolds. ¹⁶ Maria García-Parajo’s group at the Institute of Photonic Sciences in Barcelona, Spain, observed ageing motion in experiments but ascribed it to intermittent membrane protein diffusivity in regional patches, ¹⁷ which underlies behavior in simulations of protein-crowded model membranes. ¹⁰

Figure 4.

Origins and relevance of anomalous dynamics

The internal dynamics of proteins and membranes and the dynamics of surface-associated molecules are very rich and dominated by anomalous diffusion on many time scales. The physical nature of the subdiffusive dance has two faces. One is a random-walk-like, intermittent motion with scale-free immobilization events, possibly with superimposed local small-amplitude jitters. Such processes with diverging mean waiting time are inherently non-Gaussian. The other face is a viscoelastic-type anomalous diffusion governed by anticorrelated but stationary dynamics. Such antipersistent motions with power-law step correlations are normally Gaussian, ⁷ but in a heterogenous medium they may also become non-Gaussian. ¹⁰

Ageing effects, identified on many time scales, cause a perpetual decrease of the effective diffusivity over time. In cases when ageing persists over many time scales, one must consider how much time has elapsed since the system was initialized. For a protein, that initialization might be when it was synthesized by a ribosome. Knowing when the dynamics began evolving is necessary to extract relevant physical parameters such as the value of the anomalous diffusion coefficient. We may ask whether ageing in the internal motion of individual proteins will persist over longer times in the crowded environment of living cells. Due to bombardment by other biopolymers, proteins may experience considerable impacts, a kind of massage causing the unlocking of stuck configurations and thus a rejuvenation of the dynamics that resets the molecule’s internal clock and causes ageing to start again.

Scientists are still collecting evidence from experiments and simulations in an effort to understand the physical and biochemical consequences of interfacial dynamics. At ultrashort and short time scales, the observed anomalous diffusion in complex systems may point to fundamental interactions such as caging effects either in the dense array of lipids ⁸ or of the surface water. ⁷ Considering that water bridges can connect surface amino acids in a protein or connect lipid molecules in a membrane, they may not only add to the stability of protein or membrane architectures but also slow their motion. Moreover, when two biopolymers come close in the crowded cytoplasm of the cell, such water bridges may generate longer mutual contact times and thus facilitate chemical reactions and oligomerization.

The viscoelastic component in several of the observed systems appears to be a generic behavior in soft-matter systems. Because of the antipersistence of their trajectories, individual particles may remain mobile but are likely to be pushed back to their previous position over long times. Returning to the same location may increase the likelihood of repeated reaction attempts and further be beneficial in forming complexes, especially in real, highly mixed membranes. Being slow may not always be a virtue, but within cells it may underlie function.

The observed strange interfacial molecular dynamics reflect both energetic and dynamic disorder. The journey into exploring those effects and their implications for biological function has likely just begun.