Special Issue: Origin of Terrestrial Planets and the Earth–Moon System

According to current theories, the overall architecture of our solar system was established more than 4 billion years ago through an era of planet formation lasting from 10 million to several hundred millions of years. Before we began learning about other planetary systems, it was natural to assume that our own was quite representative. But in the past decade, the discovery of about 100 planetary systems around other stars has challenged this view; these systems display a broad variation in structure and most do not closely resemble our own (see the article by Tristan Guillot on page 63). ¹

Observational capabilities currently are limited to the detection of giant, Jupiter-sized planets around other stars, so that we are uncertain of the existence and distribution of smaller Earth-like planets in such systems. Thus planetary scientists rely on our own solar system as the case study for understanding the formation of terrestrial, solid planets and their satellites—such as Earth and the Moon. But our solar system as a whole may not be particularly characteristic, and recent observations suggest that the process of planet formation is one from which many potential outcomes may emerge. Theoretical models and computer simulations that strive to recreate the planetary formation process must therefore be able to account for both the primary characteristics of our system and the apparent diversity of extrasolar systems.

The planetesimal hypothesis

Understanding of stellar formation processes and observations of other young stars suggest that the early Solar System consisted of the newly formed Sun and an orbiting disk of gas and dust (see Figure 1). If one assumes it had a roughly solar composition, such a disk—also referred to as the solar nebula—would contain a mass in hydrogen gas about 100 times that contained in solid particles. Isotopic dating of the oldest known meteorites indicates that macroscopic solids began to form within the gas-rich solar nebula about 4.56 billion years ago. Observations of other stellar systems suggest that the Sun’s hydrogen-rich nebula would have been lost—possibly due to a strong solar wind or photoevaporation—after about 1–10 million years. At that time, the protoplanetary disk transitioned from one whose mass was predominantly gas to one composed solely of solid objects orbiting the Sun.

In this context, how did our solar system’s large inner objects—Mercury, Venus, Earth, the Moon, and Mars—originate? The so-called planetesimal hypothesis, which in its modern form has been developed over the past 40 years, proposes that solid planets grow from initially small particles in the protoplanetary disk through collisional accumulation, or accretion. As solid objects orbit the Sun, mutual gravitational interactions and interactions with the gaseous nebula cause their elliptical orbits to cross, which leads to collisions. The outcome of a given collision depends primarily on the ratio of the impact speed, v _imp, to the gravitational escape velocity of the colliding objects, v _ese, where $v_{\text{ese}}=\sqrt{2G\left(m_1+m_2\right)/\left(R_1+R_2\right)}$ , G is Newton’s gravitational constant, and m _i and R _i are the object masses and radii. The impact speed is a function of both v _esc and the relative velocity v _rel between the objects at large separation with $v_{\text{imp}}^2=v_{\text{esc}}^2+v_{\text{rel}}^2$ , so that v _imp is always greater than or equal to v _esc.

For v _imp ≫ v _ese, collisions result in rebound, erosion, or even fragmentation, while for lower-impact velocities, with v _imp ~ v _esc, energetically dissipative collisions lead to the formation of gravitationally bound aggregates. Repeated collisions with low impact velocities thus allow for the accretional growth of larger and larger objects.

Terrestrial planet accretion in our solar system is typically described in three stages: growth of approximately kilometer-sized “planetesimals” from dust and small particles; accretion of planetesimals into planetary embryos containing around 1–10% of the Earth’s mass M _⊕; and the collision of tens to hundreds of planetary embryos to yield the final four terrestrial planets.

The processes that control growth during the first stage are the least well understood. In general, the interaction of small, subkilometer-sized particles with the nebular gas causes their mutual impact velocities to greatly exceed their gravitational escape velocities, so that growth during two-body collisions must instead rely on either non-gravitational surface sticking forces (such as van der Waals or electrostatic forces) between the colliding particles or the collective gravitational influence of neighboring particles. Such collective effects could become important if dynamical mechanisms exist that can concentrate solids in a region of the disk; in that case, an enhanced local spatial density of particles can allow groups of particles to collapse under their self-gravity to form larger objects. Whether kilometer-sized planetesimals were formed by sticking and binary collisions or by gravitational instability—or both—is a subject of active research. ²

Planetesimals to planetary embryos

Once planetesimals become large enough (approximately kilometer-sized) for their dynamics and collisional growth to be controlled by gravitational interactions, a much better understanding exists of how growth proceeds. That understanding is due in large part to improvements in computational modeling techniques.

The rate of accretion is primarily controlled by the rate of collisions among orbiting planetesimals. Consider an annulus in the protoplanetary disk centered at some orbital radius a with volume V = Ah, where A is the mid-plane area and h is the disk thickness. If the annulus contains N small planetesimals with some characteristic random velocity v _ran relative to that of a circular orbit at radius a, then a larger embedded object of radius R will accumulate the small particles at an approximate rate $$\text{Collision}\hspace{0.17em}\text{rate}~\frac{v_{\text{ran}}N\left(\pi R^2\right)F_8}{V}-\approx n\Omega \left(\pi R^2\right)\left(1+\frac{v_{\text{esc}}^2}{v_{\text{ran}}^2}\right),$$ where F _g = 1 + (v _esc/v _ran)² is the gravitational enhancement to the collisional cross section due to two-body scattering, n = N/A is the number of particles per surface area in the disk, and h ≈ v _ran/Ω, with Ω the Keplerian orbital angular velocity. Equation 1 has its roots in kinetic theory and is known as the “particle-in-a-box” collision rate. In the case of an orbiting “box” of planetesimals, the random particle velocities arise from the planetesimals’ orbital eccentricities and inclinations and are analogous to the random thermal velocities of gas molecules confined to some volume. As this simple expression shows, the rate of collisions, and therefore of accretional growth, depends on the local Keplerian orbital velocity (which increases with decreasing distance from the Sun, so that regions closer to the Sun generally accrete more rapidly), the number density of planetesimals, and their sizes and relative velocities.

The mass and velocity distributions of a swarm of planetesimals are themselves dynamically coupled. Gravitational scattering among particles tends to increase v _ran, while energy dissipation during collisions and drag exerted on particles by the gaseous nebula both act to decrease v _ran. For a distribution of objects, an equilibrium between these processes yields v _ran on the order of the escape velocity of the object class that contains the majority of the total mass.

Interactions among orbiting particles of different masses tend to drive the system toward a state of equipartition of kinetic energy, with smaller particles having typically higher v _ran and the largest objects having the lowest. This effect is known as dynamical friction: A swarm of background small particles acts to damp the velocities of the largest objects. From equation 1, if the largest objects in a given region of the disk also have the lowest velocities, then their collisional cross sections will be significantly enhanced, compared to those of smaller objects, due to the gravitational focusing factor, F _g. For large objects, v _esc will be large compared to v _ran, which will be controlled by the smaller planetesimals that still contain most of the system’s mass. The largest objects thus grow the fastest, and a single object typically ends up “running away” with the great majority of the total available mass in its annular region in the disk. Through this so-called runaway growth, approximately lunar-sized objects, containing roughly 1% of M _⊕, grow in the inner Solar System in as little as 10⁵ years.

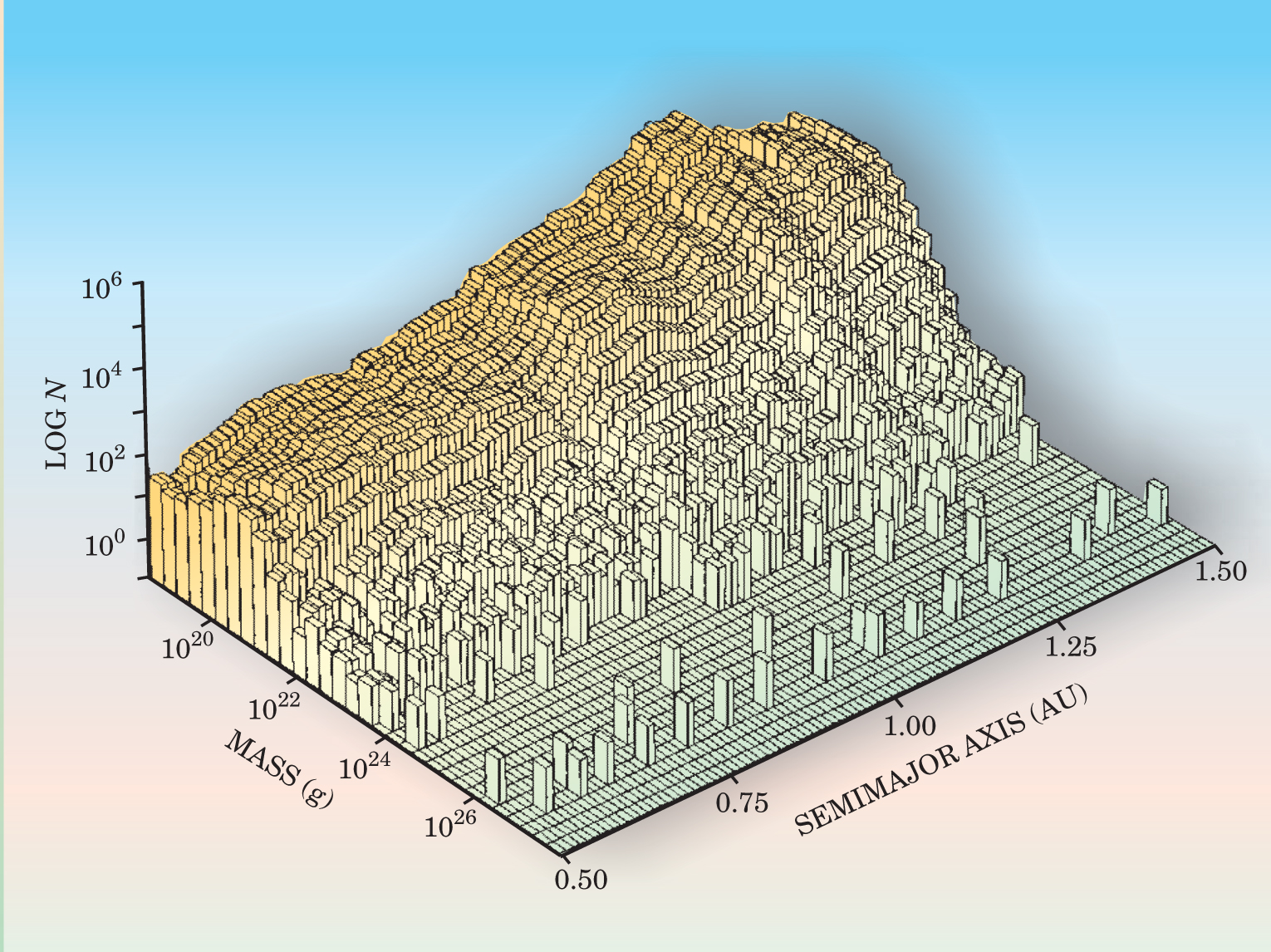
Once a large object has consumed most of the mass in its annulus, growth slows, primarily due to the reduced amount of locally available material and planetesimal velocities that have increased to around v _esc of the largest embryo. Figure 2 shows the predicted distribution of planetesimal masses in a region extending between the current orbits of Mercury and Mars from a 10⁶-year accretion simulation performed by Stuart Weidenschilling (of the Planetary Science Institute) and colleagues. ³ After a million years, 22 large planetary embryos have formed in the inner Solar System and contain 90% of the total mass. The embryos are radially well separated on nearly circular, coplanar orbits, with each containing a mass of at least 10²⁶ g (for comparison, M _⊕ ≈ 6 × 10²⁷ g).

Late-stage terrestrial accretion

Given our four terrestrial planets, the state shown in Figure 2 with tens of “miniplanets” must have been a transitory one. The gaseous component of the solar nebula is expected to have dispersed after 10⁶–10⁷ years, and with it went an important source of velocity damping for small objects. As the random velocities of small objects increased, their ability to damp the velocities of the larger embryos through dynamical friction would decrease. Mutual gravitational interactions among the embryos would then become more potent and lead to the excitation of their orbital eccentricities, mutual orbit crossings, and finally embryo–embryo collisions and mergers. As the embryos collided and accreted, the number of planets would decrease and the dynamical stability of the system would increase, until finally a few planets on stable orbits remained. The final configuration of planets would thus be established in a stochastic “process of elimination,” and a planet’s dynamical characteristics—its mass, orbital radius, rotation rate, and rotational axis, for example—would be greatly influenced by its last few large collisions.

Models of the accretion of planetary embryos into terrestrial planets were pioneered in the 1980s by George Wetherill (Carnegie Institution of Washington’s Department of Terrestrial Magnetism), who utilized a Monte Carlo approach for tracking embryo orbits. Such statistical models use analytic approximations to estimate the likelihood of collisions and to describe the effects of mutual gravitational perturbations among the planetary embryos. Those techniques, however, could not incorporate some important dynamical effects, including the potential for successive and correlated close encounters between a given pair of embryos.

In the past decade, late-stage accretion models have been revolutionized by advances in methods for directly integrating the equations of motion of objects that orbit a more massive central primary. The key breakthrough was made in 1991 by Jack Wisdom (MIT) and Matthew Holman (now at the Harvard–Smithsonian Center for Astrophysics). The Wisdom–Holman mapping (WHM) method allows for accurate integrations with relatively long integration time steps. ⁴ Whereas classic orbit integrators require 500–600 time steps per orbit, WHM saves time by analytically tracking the Keplerian motion and integrating only the small perturbations that arise from the masses of the orbiting objects, so that only a few tens of time steps per orbit are needed to ensure accuracy. The WHM method is also symplectic: Although it does not exactly conserve energy, the predicted energy oscillates about a fixed value so that energy errors do not accumulate with time. Modern techniques ⁵ based on the WHM method can track the dynamical evolution of systems of several hundred accreting planetary embryos for more than 10⁸ years. ⁶ , ⁷ Such simulations follow not only the actual orbit of each embryo but also the dynamical encounters between embryos, including collisions or close passes.

Figure 3 shows the final planetary systems produced in eight late-stage accretion simulations recently performed using such direct integration techniques by John Chambers of NASA’s Ames Research Center. ⁷ The simulated systems display a wide variety of architectures but are generally similar to our solar system’s terrestrial planets in terms of the number of final planets and their masses. A notable difference is that the planets in the simulated systems have eccentricities and inclinations much higher than those of Earth and Venus, whose orbits are very close to circular and coplanar. This difference is likely a result of simplifications made in most of the models to date, namely ignoring the influence of potential coexisting small objects or a remnant of the gas nebula in the late stage. Both would generally act to decrease eccentricities and inclinations. While it is conceptually simplest to consider a sharp division between the middle and late stages so that in the late stage such effects can be ignored, Nature may not be so accommodating. Recent models that include more initial objects or a small portion of the nebular gas have found systems with orbits closer to those in our Solar System, although accounting for the nearly circular orbits of Earth and Venus remains an open issue.

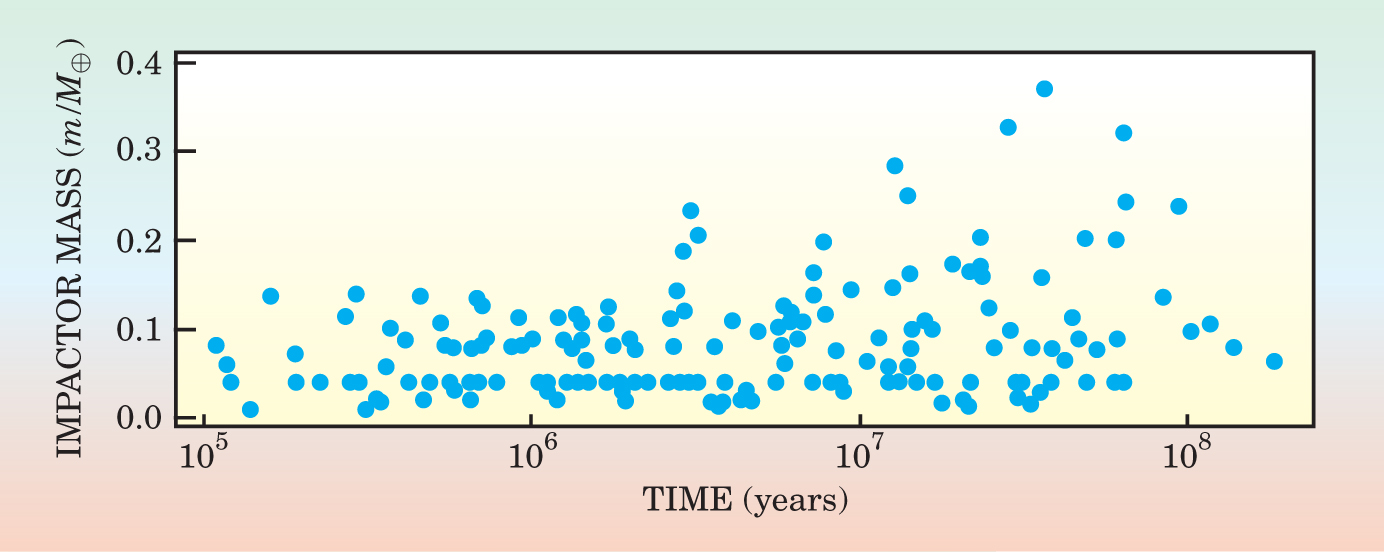
A seemingly inherent feature of the late stage is giant impacts, in which lunar- to Mars-sized objects mutually collide to yield the final few terrestrial planets. Figure 4 shows the mass of impactors as a function of time for collisions that occurred in 10 late-stage simulations performed by Craig Agnor, Harold Levison, and me at the Southwest Research Institute. ⁶ The “Earths” produced in those simulations require an average of 10–50 million years to accrete, with the largest late-stage impacts occurring predominantly in the 10⁷- to 10⁸-year time interval. The collisions display a random distribution of impact orientation, so that a final planet is as likely to end up rotating in the prograde sense (that is, in the same sense as its orbit about the Sun, as is the case for Mercury, Earth, and Mars) as in a retrograde sense (as is the case for Venus).

Origin of the Earth–Moon system

According to current thinking, the growing Earth experienced one such late-stage impact that ejected into orbit the material from which our Moon later formed. The giant impact theory for lunar origin (see the box on page 60) is favored for its ability to account for the high angular momentum of the Earth–Moon system and for the iron-poor composition of the Moon. Reconciling the type of impact required with the actual Earth–Moon system thus provides an important benchmark for terrestrial-accretion models.

The impact theory proposes that the collision that created the Moon was also the primary source of the angular momentum L _⊕-M of the Earth–Moon system. The angular momentum delivered by an impactor of mass γM _T is $$L_{\text{imp}}\approx 1.3L_{\oplus -M}b{\left(\frac{M_T}{M_{\oplus }}\right)}^{5/3}\left(\frac{\gamma }{0.1}\right)\left(\frac{v_{\text{imp}}}{v_{\text{ese}}}\right),$$ where b = sin ξ is the impact parameter normalized to the sum of the impactor and target radii, ξ is the angle between the surface normal and the impact trajectory (so that a grazing impact has b = 1 and ξ = 90°), M _T is the total combined mass of the impactor and target, and γ is the fraction of the total mass contained in the impactor. From this equation, a minimum impactor mass of about 0.08 M _⊕ is required to yield L _⊕-M in the limit of a b = 1 grazing collision for M _T ≈ M _⊕ and v _tmp ≈ v _ese. Imparting the Earth–Moon angular momentum by an oblique impact with Earth thus implies an impactor roughly the size of Mars—that is, about 0.1 M_⊕.

For impact-ejected material to achieve Earth-bound orbit, some modification to standard ballistic trajectories must occur, otherwise ejecta launched from the planet’s surface either re-impacts or escapes. Two nonballistic effects are gravitational torques due to mutual interactions among ejected material or to interaction with a nonspherical distortion of the target planet, and pressure gradients associated with vaporization. These effects become important for large impacts: the first when the impactor is a significant fraction of the target’s mass, and the second when the specific impact energy (that is, the impact energy per unit mass) exceeds the latent heat of vaporization for rock, about 10¹¹ erg/g, which occurs for v _imp ≳ 5 km/s.

For a lunar-forming impact, the expected impact velocity is around 10 km/s, and both torques and vaporization could be important. Modeling potential lunar-forming impacts thus requires a full hydrodynamic approach that includes both an explicit treatment of self-gravity and an equation of state appropriate to describe the thermodynamic response of material subjected to very high impact energies and pressure.

Models of lunar-forming giant impacts have primarily used smooth particle hydrodynamics. SPH, developed over the past 25 years, ⁸ represents a significant advance in the modeling of deforming and spatially dispersing hydrodynamic systems, including giant impacts. SPH is a Lagrangian method, which is advantageous because its numerical resolution tracks the spatial distribution of the evolving material, and compositional histories can be easily followed. In SPH, a planetary object is represented by a great number of spherically symmetric overlapping “particles,” each containing a quantity of mass of a given composition, whose three-dimensional spatial distribution is specified by a density-weighting function, the kernel, and by the characteristic width of the particle, the smoothing length.

For impacts between planet-scale objects, each particle’s kinematic variables (position and velocity) and state variables (internal energy and density) evolve due to gravity, compressional heating and expansional cooling, and shock dissipation. The forces between particles thus include attraction due to gravity, which acts inversely with the squared distance between particles, and a repulsive pressure for adjacent particles closer than approximately the sum of their smoothing lengths. The equation of state relates a particle’s specific internal energy and density to pressure as a function of input material constants.

The use of SPH in modeling lunar-forming impacts was pioneered by Willy Benz (now at the University of Bern), Alastair Cameron (now at the University of Arizona), and colleagues in the 1980s. ⁹ The general approach in performing such numerical impact experiments has been to vary the four impact variables—b, M _T, γ, and v _imp— of equation 2 in a series of simulations to determine what sets of impact conditions yield the most favorable results. The challenge is that the possible parameter space is large and individual impact simulations are computationally intensive. Recent works ¹⁰ , ¹¹ have successfully identified impacts capable of simultaneously accounting for the masses of Earth and the Moon, the Earth–Moon system angular momentum, and the lunar iron depletion.

Figure 5 shows a time series of a lunar-forming impact simulation ¹¹ using high-resolution SPH and a sophisticated equation of state first developed at Sandia National Laboratories and recently improved by Jay Melosh of the University of Arizona’s Lunar and Planetary Laboratory ¹² to include a treatment of both molecular and monatomic vapor species. The simulation offers the most realistic treatment of vaporization of any SPH simulations performed to date, and each impact simulation requires several days of computational time on a high-speed workstation.

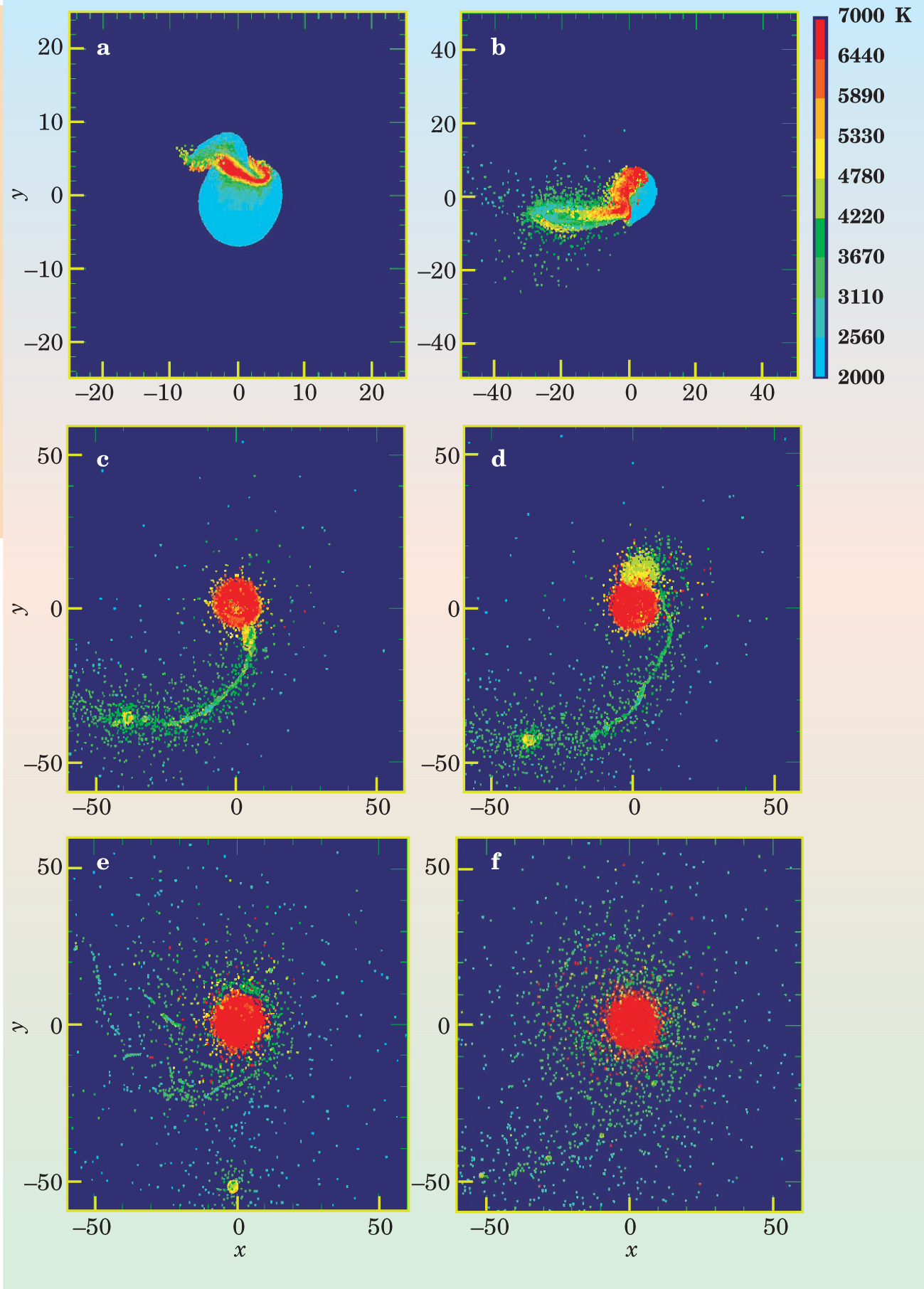
In the impact simulation, the colliding objects are described by a total of 60 000 SPH particles. The normalized impact parameter is b ~ 0.7 (that is, a 45° impact angle); the impactor contains 1.2 times the mass of Mars; the impact velocity is 9 km/s; and the impact angular momentum L _imp = 1.25 L _⊕-M . Before the impact, both objects are differentiated into iron cores and silicate mantles—a reasonable assumption given the amount of heating that would have been induced as the objects accreted to sizes this large. Both are 30% iron by mass.

After the initial oblique impact (Figure 5(a), after about 20 simulated minutes), a portion of the impactor is sheared off and continues forward ahead of the impact site. A distorted arm of impactor material extends to a distance of several Earth radii, and the proto-Earth surface and the inner portions of this arm rotate ahead of the more distant material (Figure 5(b) at 80 minutes). This configuration provides a positive torque to the outer portions of material, helping them to gain sufficient angular momentum to achieve bound orbit. In the 3- to 5-hour time frame, the inner portions of the orbiting material (composed primarily of the impactor’s iron core) gravitationally contract into a semicoherent object (Figure 5(c)) that collides again with the planet after about 6 hours (Figure 5(d)). Thus at this point, most of the impactor’s iron has been removed from orbit. The outer clump of impactor material (Figure 5(e))—composed entirely of mantle material—passes close to Earth and is sheared apart by planetary tidal forces that leave a circumplanetary disk after about a day (Figure 5(f) at 27 hours).

At the end of this impact, the resulting planet and disk are a close analog to that needed to produce the Earth–Moon system. The planet contains about an Earth mass and its rotational day is about 4.6 hours, and the orbiting disk contains about 1.6 lunar masses. Of the orbiting material, approximately a lunar mass has sufficient angular momentum to orbit beyond a distance known as the Roche limit, located about 3 Earth radii from the center of the Earth for lunar-density material. Inside the Roche limit, planetary tidal forces inhibit accretion; it is within this distance, for example, that planetary ring systems are found around the outer planets. Accretion will occur for material orbiting beyond the Roche limit, so the orbiting disk produced by this impact would be expected to yield a lunar-sized moon at an initial orbital distance of about 3–5 Earth radii. The short 4.6-hour day of postimpact Earth causes the distance at which the orbital period is equal to the terrestrial day—the so-called synchronous radius—to fall within the Roche limit, at about 2.2 Earth radii. Because the Moon forms beyond this distance, tidal interaction with Earth will lead to the expansion of the Moon’s orbit while Earth’s rotation slows.

The impact must also account for the Moon’s iron depletion. Whereas the colliding objects in Figure 5 both contained 30% iron by mass, the orbiting material is derived overwhelmingly from the outer mantle portions of the impactor. The protolunar disk contains only a few percent iron by mass, with the iron originating from the impactor’s core. The lunar-forming impact dramatically raises Earth’s temperature, with about 30% of the planet’s mass heated to temperatures in excess of 7000 K. Thus postimpact Earth would have been engulfed in a silicate vapor atmosphere, with the majority of the planet likely in a molten state.

Since large collisions appear typical in the late stages of terrestrial planet formation, how often do such impacts produce satellites? Results of impact simulations suggest that low-velocity, oblique collisions (those with b > 0.5) between planetary embryos generate some amount of orbiting material around the larger of the colliding objects. For random impact orientation, the most likely value for b is 0.7 (which is what has been found to be optimal for the Moon-forming impact), and 75% of all collisions will have b > 0.5. Thus the inner Solar System may have initially contained many impact-generated satellites, with the majority lost as they were destroyed or dislodged by subsequent impacts or as their orbits contracted due to tidal interactions with a slow- or retrograde-rotating planet.

Isotopic timing constraints

The general agreement between the type of impact apparently required to yield Earth’s Moon and those predicted by accretion simulations provides an important corroboration of current models of solid-planet formation. Other important pieces of independent evidence are the formation times implied by the isotopic compositions of Earth and the Moon.

A key development in the past decade has been the use of the hafnium–tungsten chronometer for dating planetary core formation and giant impacts. ¹³ Radioactive ¹⁸²Hf decays to ¹⁸² W with a halflife τ_1/2 of 9 million years. A critical distinction between hafnium and tungsten is that hafnium is lithophilic (“silicate-liking,” tending to be concentrated in oxygen-containing compounds such as silicates), whereas tungsten is siderophilic (“iron-liking,” or tending to enter metallic phases). During core formation in a planetary object, whatever tungsten is present in the planet’s mantle—radiogenic ¹⁸²W as well as nonradiogenic W-isotopes such as ¹⁸³W and ¹⁸⁴W—will be largely removed from the mantle and incorporated into the iron core, while hafnium will remain in the mantle. Thus the mantle of a differentiated planetary object will have a Hf/W ratio larger than that of bulk Solar-System composition. The bulk Solar-System composition can be inferred from the composition of primitive meteorites, called chondrites.

The Hf/W ratio and W-isotope compositions of a differentiated object such as Earth provide timing constraints on the formation of its core and potentially on the timing of its last large collision. The tungsten composition of chondrites includes both nonradiogenic isotopes and ¹⁸²W produced by the decay of primordial ¹⁸²Hf, and the chondritic W-isotope composition provides a reference value believed indicative of early Solar System abundances. If a planet’s core formed on a timescale shorter than about 5τ_1/2, its mantle, compared to chondrites, would contain excess ¹⁸²W (relative to the abundance of other W isotopes) produced by decay of ¹⁸²Hf after core formation. If the core formed later when ¹⁸²Hf was essentially extinct, all isotopes of W would have been equally depleted by incorporation into the iron core, leaving the mantle with a chondritic W-isotopic composition.

Earth’s mantle contains an excess of ¹⁸²W compared to the most recent assessments of chondritic W-isotope composition, ¹⁴ , ¹⁵ which implies that Earth’s accretion and core formation were largely completed in 10–30 million years (see Physics Today, January 2003, page 16 ). The Moon has a similar Hf-W–derived formation time of about 25–30 million years. ¹⁴ These specific timings can be affected by model assumptions, such as the degree to which accreting material isotopically equilibrates with Earth’s mantle. ¹⁶ However, in general, the Hf–W timings and the late-stage dynamical models both yield estimates in the 10- to 50-million-year time interval for planetary accretion, giant impacts, and the final episodes of terrestrial-planet core formation. Broadly similar formation times of 10⁷ to 10⁸ years also result from other isotopic systems such as uranium–lead, iodine–xenon, and plutonium–xenon. ¹⁶ If the terrestrial planets had grown to their final sizes through runaway growth, their formation times would have been much shorter, on the order of 10⁶ years or less. The agreement between the dynamically and geochemically derived timings thus provides significant support to the existence of a protracted phase of late accretion dominated by large impacts.

Whereas early models proposed that Earth-like planets form through the orderly accretion of nearby small material in the protoplanetary disk, current work instead suggests that solid planets are sculpted by a violent, stochastic final phase of giant impacts. The implication is that our terrestrial planets—and Moon—may only represent one possible outcome in a wide array of potential solar-system architectures. With future space missions (such as NASA’s Terrestrial Planet Finder) devoted to detecting Earth-like planets around other stars, we may someday be able to directly test such concepts.

The author gratefully acknowledges support from NSF and NASA.