Solving quantum chemistry problems on quantum computers

“Quantum” may not be the first word that comes to mind when thinking about chemistry. But at the atomic level, the physical and chemical properties of molecules can be affected by quantum mechanical interactions. The spin of an electron, for example, is a property that is fundamentally quantum, and electron spin affects the reactivity of the molecule that the electron is part of. Every chemical reaction, therefore, is guided by the laws of quantum theory.

The modeling of quantum properties, however, is difficult, and thus the R&D costs for industries that need to understand the effects are extraordinary. A pharmaceutical company pays an average of about $2.4 billion to develop a new drug. Much of that cost is in preclinical research because chemists usually rely on trial-and-error processes to test the suitability of roughly 1000 small molecules for clinical trials. Only about 10% of clinical trials result in successful products. Many chemical companies, therefore, are on a quest to improve the efficiency of modeling molecules. ^{1 , 2}

One top priority in the field of computational chemistry is to replace the current trial-and-error approaches with direct modeling that has sufficient accuracy to resolve all relevant processes, such as reaction rates of molecules at room temperature. With such accuracy, a system’s behavior could be predicted, which would be a pivotal benchmark for quantum chemistry. Although many methods exist for modeling quantum effects on classical high-performance computers, they struggle to reach the required accuracy for certain types of chemical systems, particularly large systems of hundreds or thousands of molecules with either strong electronic correlations or coupled vibrational and electronic correlations.

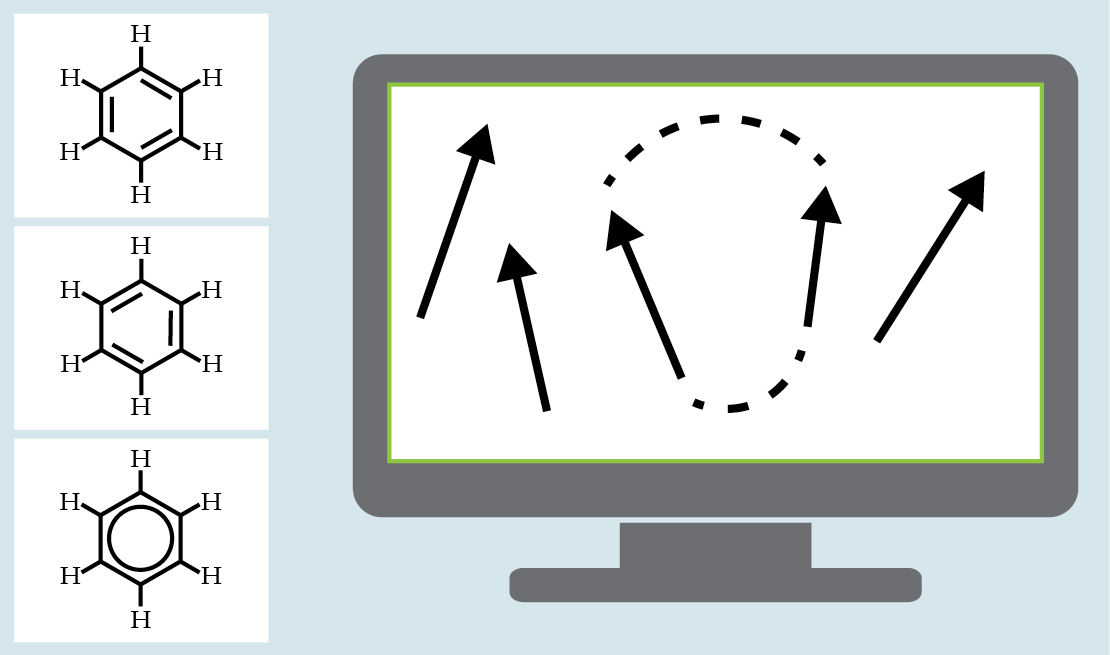
Medium-sized strongly correlated systems of tens to hundreds of molecules, however, could soon be analyzed more efficiently with a quantum computer than with a classical computer (see figure 1). A small quantum computer with around 100 error-protected qubits, for example, may be capable of calculating the energy of around 100 spin orbitals, each of which is a wavefunction that specifies the probability of the position and spin of an electron. ^{3 , 4} That capability would be useful for numerous applications, including the search for transition metals that serve as efficient catalysts in chemical processes.

Figure 1.

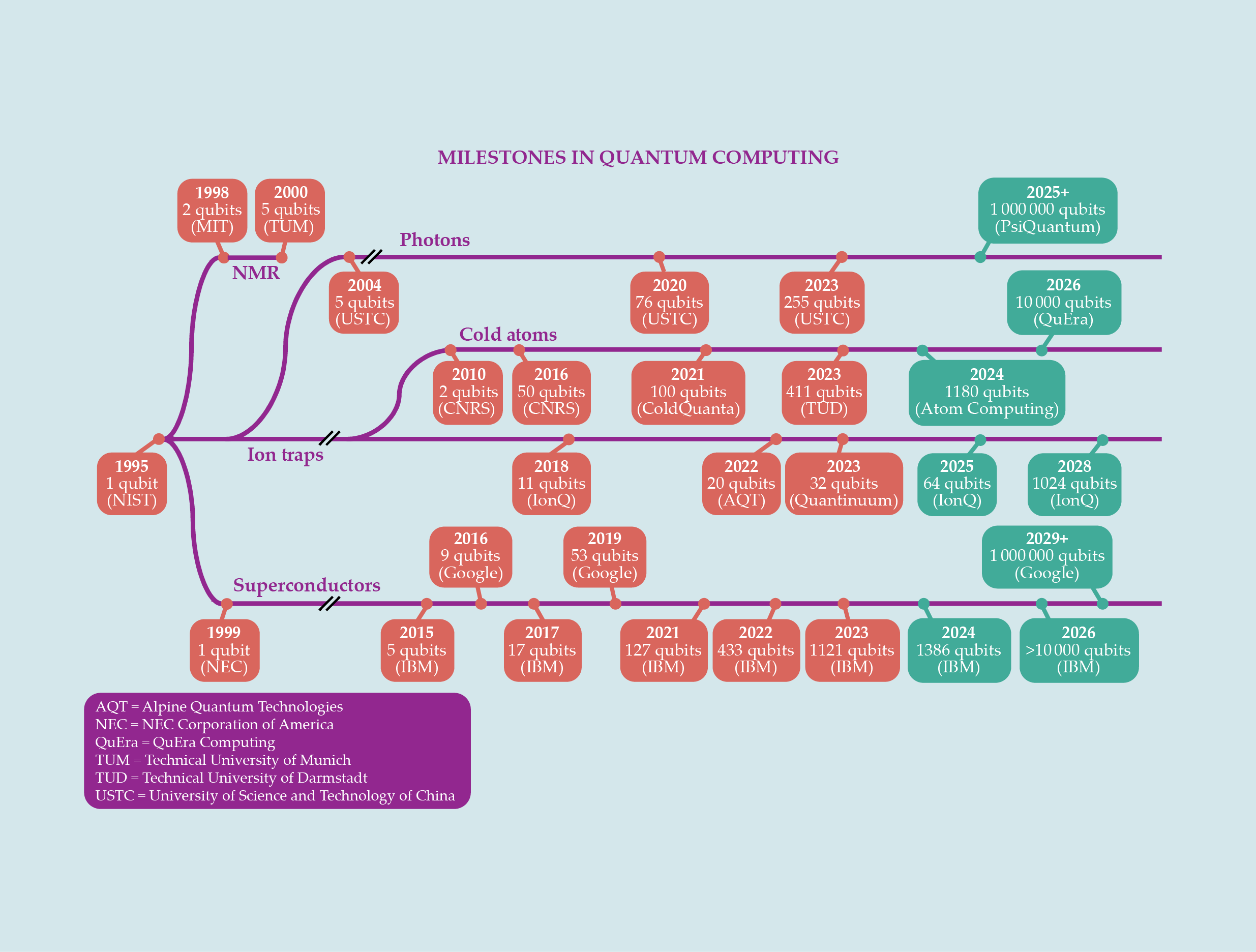
Take the Haber–Bosch process, for example, which has been used for more than 100 years to fabricate ammonia for fertilizers. The process consumes about 2% of the world’s energy. In the long run, quantum chemistry could simulate how various catalysts could improve the nitrogen-reduction reaction and other reactions in the Haber–Bosch process to make it more energy efficient. For now, such simulations aren’t possible because of the large number of qubits required. An error-resilient simulation of the Haber–Bosch process would need around a million physical qubits. Many companies are working on building quantum computers with substantially larger qubit numbers. Some have boasted that the 1 million–qubit mark could be reached within this decade (see figure 2).

Figure 2.

Quantum computing and quantum algorithms

The classical computing methods for chemistry often aim to investigate the energy landscape of a given system. A chemical system’s ground state—the lowest energy state of a given molecule—is a quantum wavefunction of the configurations of all nuclei and electrons. But to determine the ground state, researchers often investigate only a small subset of all possible configurations. The complete set is too large to be thoroughly analyzed on a classical computer within a reasonable time because of entanglement that’s created by the quantum superposition of some of the molecule’s states. To ignore many of those configurations and make the analysis more tractable, classical computing algorithms use several approximations, some of which are detailed in box 1.

In addition to a molecule’s ground state, dynamical processes that occur at finite temperature are important to describe. For strongly correlated systems and large systems with several hundred atoms, the computations are difficult, and approximations will typically struggle to produce highly accurate results. The approximating tools are useful only in cases in which quantum effects play a negligible role—for example, in the calculation of diffusion and in the study of conformal processes, such as protein folding. Such calculations are not expected to be done on quantum computers anytime soon, given the large system sizes that need to be simulated.

The basic idea behind quantum computing is the replacement of the classical bit, which can take a value of 0 or 1, with the qubit, which can exist in a superposition of on and off states. Among all the possible states, some exhibit unique quantum properties: The measurement of one qubit’s state may influence the probability of the measurement of another qubit’s state. In that case, the qubits are entangled. So long as the qubits are resilient to noise and errors from external sources have been corrected, a quantum computer’s storage capacity scales exponentially. Because two qubits can be found in a superposition of four possible states, three qubits can be found in a superposition of eight possible states, and so on, n qubits can be used to store 2ⁿ bits of information. Once the quantum computer has around 60 qubits, its storage capacity quickly surpasses that of classical computers.

Some of the highly entangled states of the quantum computer can serve to efficiently describe chemical systems that are predominantly driven by quantum effects and that may lack a classical description. In fact, quantum computers may support fundamentally different approaches to computations and simulations. The so-called quantum advantage can be reached when quantum computers perform applications more quickly and efficiently than classical computers. (For more on the design of quantum computers, see the articles by Anne Matsuura, Sonika Johri, and Justin Hogaboam, Physics Today, March 2019, page 40 ; and by Harrison Ball, Michael Biercuk, and Michael Hush, Physics Today, March 2021, page 28 .)

For classical computers, a computation proceeds through logic gates, which use one or more binary inputs to produce a single binary output. A quantum computer works similarly but with quantum gates. In the future, the simulation of a chemical system could be accomplished by breaking down the individual operations in a simulation into, for example, elements of a universal quantum computing gate set. With that approach, many simulations could run on the same computer.

The approach, however, requires a substantial amount of qubits and other computational resources. And given the number of logical operations to be performed, the approach increases noise sensitivity and the risk of errors in the computation. Indeed, how faithfully quantum gates are executed on an actual device is still a critical challenge for quantum computation. Various factors, including unwanted interactions of qubits with the environment and imperfect qubit controls, can degrade a computation.

Preventive methods, such as the creation of multiple copies of stored information, have been specifically adapted to quantum computers and are called quantum error correction. Although the methods require large numbers of qubits—some early estimates have used 1000 qubits to obtain a single error-protected qubit—innovation in error correction is proceeding fast. Recent breakthroughs in error control ^5–7 have the potential to usher in the era of fault-tolerant quantum computing (FTQC). That’s when quantum computers will be programmable and their results will be trustworthy, much like the classical computers of today. In fact, there are signs that the transition into the FTQC era is already happening. ⁸ The most interesting time for all industries, especially the chemical industry, will be when the quantum advantage can be fully harnessed with large, fault-tolerant quantum computers.

Currently the industry is in the noisy intermediate-scale quantum (NISQ) era. NISQ devices can execute gate-based algorithms, although with limited accuracy. The gate-based approach could be skirted in favor of less demanding analog quantum simulations. Molecular dynamics simulations or other methods could bypass the gate decomposition and directly emulate the time evolution of a real system of interest. Whether the quantum advantage can be realized in the NISQ era with such an approach is currently being investigated.

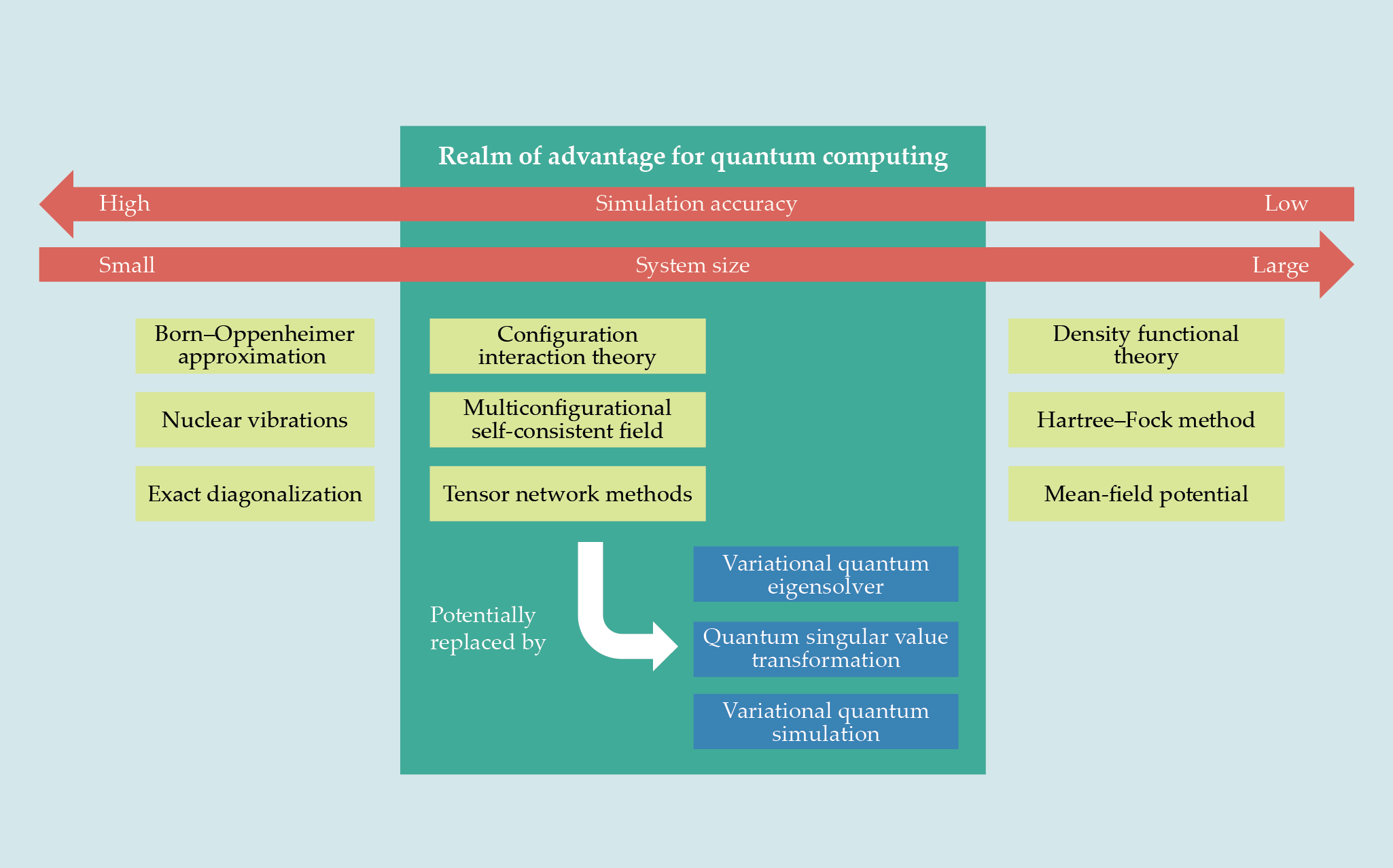
No matter the chosen approach, a key element for advancing quantum computing specifically for chemistry is the ongoing development of quantum algorithms that bring together quantum information theory and classical techniques. Because an n-qubit quantum computer can manipulate and store 2ⁿ bits of information at the same time, quantum algorithms can potentially work quite differently from classical computer algorithms. Such algorithms are, however, still in their infancy, and the field has not yet converged on a single approach that can guarantee quantum advantage. The current list of promising algorithmic methods for simulating quantum chemistry problems is long, as shown in figure 3, and highlights the amount of work that has already been done on the theoretical side to realize the next stage of quantum chemistry simulations. For more details about some specific approaches, see box 2.

Figure 3.

Hardware

With many algorithms in place and in development, the attention of the industry, eager to exploit the expected quantum advantage, has turned toward the hardware providers and the question of when sufficiently reliable quantum computing devices will become available. Several companies are relying on a variety of technical platforms, including spin qubits, topological systems, and photonic quantum computing, to develop quantum computers. The winning approach may involve the integration of several technologies. The market will likely follow a winner-takes-all mentality, but for now, all those technologies are under consideration.

The goal is to develop a universal device that is capable of executing all possible quantum algorithms. To prevail, any of the platforms being studied will need to have several issues addressed. According to a majority of the community, two of the technologies hold great promise: trapped atoms ^{9 , 10} and superconducting qubits. ¹¹ (See figure 4 for an overview.)

Figure 4.

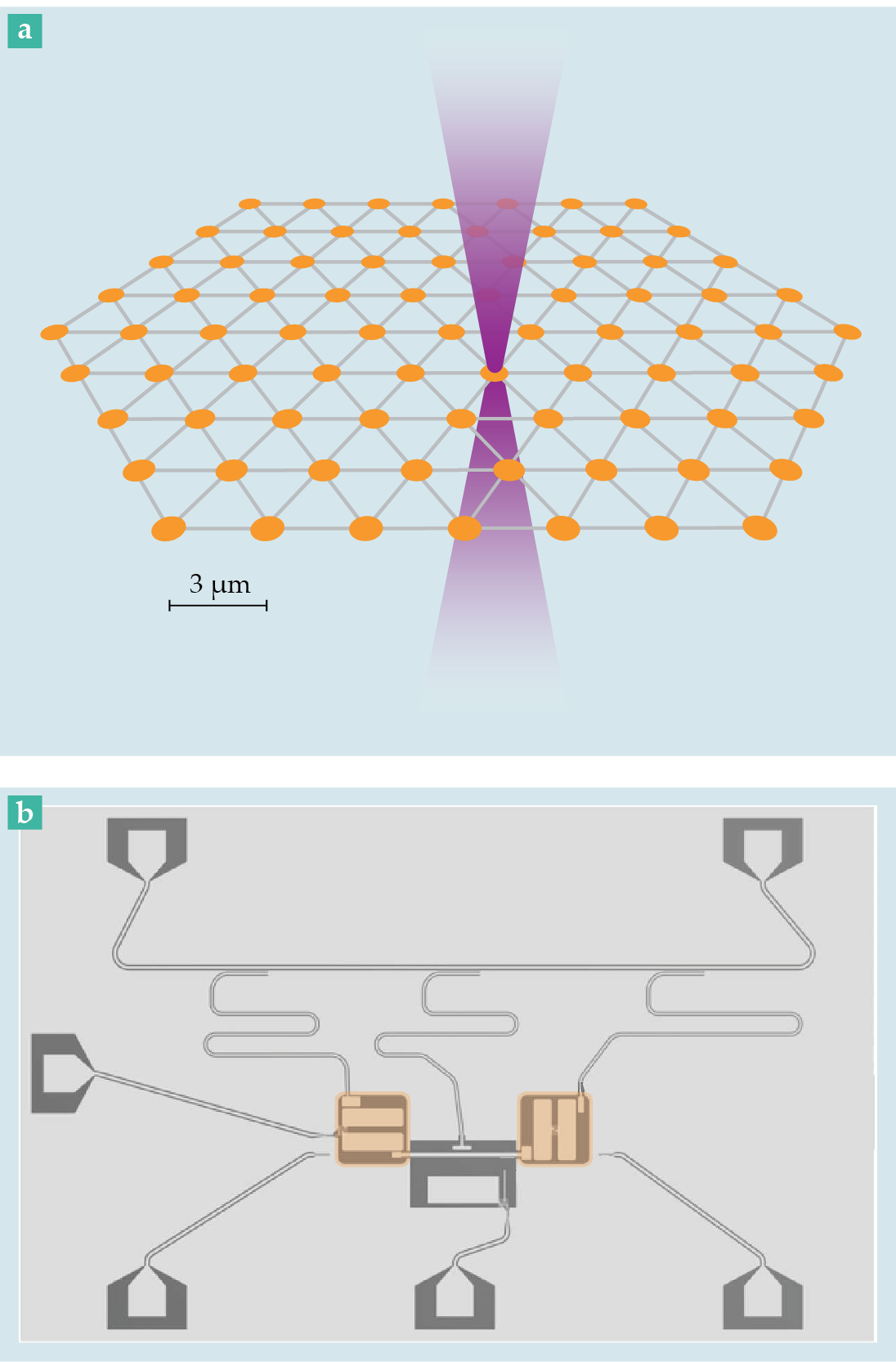
Among the first approaches that researchers used were laser cooling techniques, which individually trap atoms and cool them to temperatures less than 1 mK. When ionized, atoms can be trapped by electric fields; for neutral particles, optical tweezers can trap them. In both approaches, a qubit is made when two energy levels—usually the ground state and some excited state—are coupled by electromagnetic radiation, and the result is a single-qubit quantum gate. Two-qubit gates can be formed if the trapped atoms interact, either through electrostatic forces for trapped ions or through van der Waals or dipolar interactions for neutral atoms.

In recent years, 1D and 2D arrays of neutral atoms trapped in optical tweezers have demonstrated highly accurate multiqubit operations and have become a powerful platform for quantum simulations and computations. In that approach, strong interactions between atoms in adjacent tweezers are controllably induced when the atoms are excited to Rydberg states, high-energy states with large principal quantum numbers and large spatial extents.

A key strength of Rydberg atoms as a platform is their demonstrated scalability. The number of qubits in such a system can range from hundreds to tens of thousands. By dynamically reconfiguring the Rydberg atom arrays, researchers can engineer arbitrary lattice geometries and connectivity for various types of quantum gates. The qubits can then be read out by fluorescence imaging of the single atoms with a highly sensitive CCD camera and an imaging system with micrometer resolution. The technology of reconfigurable atom arrays is poised to be instrumental in advancing the FTQC era in the next few years.

For algorithm-based applications, one main challenge has been the limited gate accuracy because of technical imperfections and physical effects that lead to decoherence. Recent breakthrough experiments, however, have demonstrated remarkable technological achievements, including the operation of two-qubit gates with accuracies of 99.5% and error suppression with logical operations made with tens of logical qubits, ⁸ which are themselves made of many physical qubits.

Another promising technology platform, superconducting quantum circuits, takes a different approach than atoms to develop qubits. On a superconducting platform, similar to a classical computing structure, an electric circuit is nanofabricated on a silicon chip. Its components are classical elements, such as inductors and capacitors. But on top of those, the circuit integrates superconducting elements, so-called Josephson junctions. With those junctions, the circuit functions as a qubit that exhibits a transition frequency between the ground state and the excited state that’s typically between 300 MHz and 5 GHz, depending on the precise design and architecture of the superconducting circuit. Since each superconducting quantum circuit is individually fabricated, they are often called artificial atoms. They offer a rich parameter space of possible qubit properties and operation regimes with predictable performance.

Many industrial players have already created large devices with hundreds of superconducting qubits and peak accuracies of 99.9% for two-qubit gates. The circuits, however, require expensive, complex nanofabrication technology for optimal results. Another limitation is that, like any other qubit, superconducting qubits are susceptible to noise: Temperature fluctuations, for example, may cause the qubits to be excited to higher energy levels and introduce errors in computations. For that reason, any superconducting quantum processor unit needs to be operated at low temperatures, around 10 mK. (For more on error correction for superconducting qubits, see the article by José Aumentado, Gianluigi Catelani, and Kyle Serniak, Physics Today, August 2023, page 34 .)

With modern cryostats, it is possible to reach those low temperatures. Their maintenance, however, might be challenging if the system is scaled to a large number of qubits. Each qubit is typically controlled and read out via a dedicated wire, which connects the quantum processor with the control software outside the cryostat. To have thousands of cables to address each qubit individually is a major routing challenge because such a dense wiring arrangement causes unwanted heat radiation, which disturbs the qubits. Hence, ideas are emerging in the field for how to decrease the wiring complexity, such as using the same wire for multiple qubits, known as multiplexing, and using control electronics that work at cryogenic temperatures.

Although those and many more technical challenges apply to nearly all platforms, existing prototypes already have demonstrated that, in principle, the cold-atom technology and the superconducting circuits work. Several companies are researching error-mitigation strategies and are encoding logical qubits on superconducting and trapped-atom platforms. ¹² Even applications to chemical systems have been demonstrated on a superconducting quantum computer with 20 qubits. ¹³ The achievement makes it the largest simulation of quantum chemistry on a quantum computer so far. With the proof of principle achieved, the central questions now are, What are the remaining steps needed to close the gap to real-life use cases, and Who is going to accomplish them?

The MOQS consortium

Quantum computing for quantum chemistry still faces many challenges, not least the high error rates and low qubit numbers of existing hardware. Considerable developments are needed to both build a powerful quantum processor unit and identify appropriate algorithms. The most prominent companies pushing the boundaries are tech giants in the US, such as Google, Microsoft, and IBM, and more than 100 quantum startups have emerged worldwide.

The quantum industry in the European Union is growing fast, predominantly in the academic sector. The EU trains the highest number of master’s students in quantum tech–related fields: about 135 000, according to an April 2023 analysis by McKinsey & Company. To connect new knowledge leaders with the emerging quantum industry, the Horizon Europe program has funded the European Training Network for Molecular Quantum Simulations (MOQS).

The MOQS consortium includes several companies and research institutions from across the EU. With its expertise, the consortium trains about 15 PhD fellows annually in multiple disciplines, such as experimental physics and theoretical chemistry. In addition to searching for efficient quantum algorithms and tackling the technical challenges, the MOQS fellows work on a broad set of topics at the cutting edge of quantum computing research. In some cases they have already broken new conceptual ground.

At IBM Research in Zurich, Switzerland, for example, a MOQS fellow has investigated an alternative to the usual measurement in the computational basis of the logical values 0 and 1. Known as the positive operator-valued measurement, it has advantages for calculating the expectation values of operators, which are important in many quantum algorithms. The measurements had been assumed to need extra qubits for their implementation, which makes their realization harder and more resource demanding. The recent MOQS results show that positive operator-valued measurements can be efficiently implemented in existing superconducting quantum computing platforms without the use of additional qubits. ¹⁴

At Eindhoven University of Technology in the Netherlands and the University of Strasbourg in France, MOQS fellows have looked into quantum logic gates based on interacting Rydberg atoms. The optimized laser pulses that have been developed ¹⁵ should make it possible to reach gate accuracy of more than 99.9%, with 99.5% just recently demonstrated. ¹⁶ In addition, new results from Ljubljana, Slovenia, are helping to unravel the complicated dynamics of interacting quantum many-body systems. ¹⁷

A close connection to industry further guarantees that the doctoral students involved with MOQS obtain the necessary skills to propel the field of quantum chemistry forward. Major companies, including BASF, HQS Quantum Simulations, and Bosch, are involved in the consortium and ensure that the research projects lead to applicable use cases for businesses. Only such close alignment can shorten the expected time frame to the quantum advantage.

Early adoption

The chemical industry’s interest in quantum computing stems from the hope that quantum approaches might help in the development of new and better products at lower costs and in less time. Nonetheless, businesses will likely have to wait several years before quantum computers will create real benefit. As mentioned, it may be possible to simulate molecules with 100 spin orbitals on a 100-qubit quantum computer, but even that is still far from the long-term goal of the pharmaceutical companies. When they design new medicines and materials via quantum simulation, 95% of approved drug molecules are larger than 200 spin-orbital systems. ³

Another factor to consider is error correction, in which up to 1000 physical qubits are combined to create a single error-resilient logical qubit. Only with error-resilient qubits can algorithms function properly and provide a quantum speedup over classical algorithms. Many recent advances have shown how to realize error correction on quantum devices with several hundred qubits. ⁸ So the field may transcend the NISQ era sooner than anticipated.

The three of us are hopeful that the chemical industry can see a quantum advantage in computing toward the end of this decade—or maybe sooner if progress in technology proceeds at the currently staggering pace. In addition, molecular modeling is not the only area where quantum effects can be useful. Although chemical companies may see the benefits first, quantum computing stands poised to affect many other industries, including those that design and develop catalysts and new materials, batteries, semiconductors, magnets, and high-temperature superconductors.