Solid-state cooling with caloric materials

On a hot summer day, many of us are fortunate enough to have access to a refrigerator stocked with ice-cold drinks in a comfortable, humidity-controlled room. From domestic appliances to stadium-sized central air-conditioning systems, cooling and air-conditioning today are often seen as basic necessities. Indeed, HVAC (heating, ventilation, and air-conditioning) is a multibillion-dollar industry. There is always a demand for more efficient, inexpensive, and versatile cooling equipment.

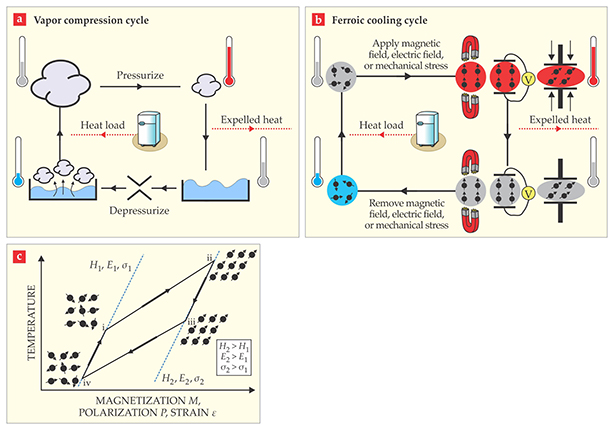
Vapor compression technology has been around since the early 19th century, and it continues almost unchallenged as the dominant means of cooling. In a vapor compression cycle, as seen in figure 1a, pressure converts the refrigerant gas to a liquid state and latent heat associated with the phase transition is unleashed. When the pressure is released and the refrigerant changes back to the gaseous state, the latent heat is reabsorbed, drawn in from the environment to be cooled.

Our ability to cool using volatile liquid refrigerants has had many socioeconomic benefits. In the 1950s the explosive growth of major cities in the American Southwest was spurred by advances in cooling technologies. Today around 50% of US energy use in the summer is for some form of cooling. However, the environmental impact of the high global-warming potential (GWP) of vapor compression refrigerants based on hydrofluorocarbons and hydrochlorofluorocarbons is a topic of ongoing discussion. What is particularly worrisome is that consumers in developing countries continue to use a large number of low-performance vapor-compression-based air conditioners that employ high-GWP refrigerants.

Thus the advent of alternative cooling technologies is a welcome development. The field of nonvapor compression HVAC is actually a crowded arena with many burgeoning technologies. In addition to the three main solid-state cooling technologies—magnetocaloric, electrocaloric, and elastocaloric—covered in this article, there are several others, including gas-based thermoacoustics (described by Gregory Swift, Physics Today, July 1995, page 22 ), the Brayton heat pump, Stirling coolers, and mature but inefficient solid-state thermoelectrics (see the article by Gerald Mahan, Brian Sales, and Jeff Sharp, Physics Today, March 1997, page 42 ). Many of the alternate technologies have been around for some time, and because of the changing landscape of cooling appliances and increasing consumer demands, they are all vying to dominate their respective niche applications.

In recent years the HVAC industry has made significant strides in reducing the refrigerants’ GWP, measured in equivalent carbon dioxide emission for the life cycle of a machine. Some of the newest refrigerants have a minimal GWP. As a result, the main opportunity for alternative green cooling technologies will be in increasing overall system efficiency. Measured in coefficient of performance (COP), system efficiency can be expressed as the ratio of the delivered cooling energy per cycle to the total input wattage for the machine’s operation. The current state-of-the-art commercial vapor compression cycle has a COP of about 3.6. This article focuses on solid-state alternatives.

Entropy, heat, and phase transitions

Many readers will be familiar with an easy home experiment that helps shed light on how a cooling cycle with a solid refrigerant can work. If you quickly stretch and hold a piece of rubber, it heats up. You can use your lip to check. The reason for that elastocaloric effect is that upon rapid stretching, the entropy associated with the rubber molecules, which are now more ordered, is lowered. Stretched quickly (adiabatically), there is insufficient time for the rubber to exchange heat with the surrounding air. Therefore, the entropy is exchanged internally with the vibrations of the atoms that make up the rubber molecules. In short, swiftly stretching rubber heats it; subsequent relaxing will cool it. A refrigeration cycle can be envisioned in which rubber is repeatedly stretched and released, and heat is exchanged with the environment.

A similar cycle can be devised using any material in which an internal degree of freedom can be ordered and disordered. Such materials might have variable magnetic spins, electric dipoles, or structural arrangements. Figure 1b shows the schematic of how each of those orderings can be used to run a cooling cycle. But the largest heating and cooling effects will be found in materials that undergo a spontaneous phase transition at the desired temperature. For those special materials, a relatively small driving field can be applied or released around that temperature and tip the thermodynamic balance between one state and another. For example, rubber’s potential as a refrigerant would be even greater if it spontaneously ordered and disordered near room temperature.

We call all materials considered as potential refrigerants “ferroic” to signify that some form of order is being manipulated. The research community has so far grouped ferroics by the driving field that is required to provide cooling. ¹ Thus barocaloric materials, or simply barocalorics, are those that are driven by a change in hydrostatic pressure and undergo a phase transition that involves altering the crystalline symmetry or crystal lattice parameters. Conventional liquid–gas refrigerants could be considered barocalorics by extension. Elastocalorics behave in a similar way, but through the action of an applied uniaxial stress. Magnetocalorics are driven by a magnetic field, and electrocalorics by an electric field. The ideal thermodynamic cycle for solid-state cooling is shown in figure 1c. Typically, values of the isothermal change of entropy, ΔS, and of the adiabatic change of temperature, ΔT_ad, are used to characterize ferroic refrigerants.

For vapor compression, the refrigerant is also the circulating fluid. But the refrigerant materials discussed in this article are all solids, so an exchange fluid is needed to transport heat to and from the refrigerant. The chilled fluid can then, in turn, be used to operate end-user appliances such as refrigerators or air conditioners. The circulatory system is often called either a regenerator or a heat-recovery system and represents an active field of research that is beyond the scope of this article.

Magnetocaloric cooling

Magnetic refrigeration is arguably the most well developed of the ferroic-cooling technologies. The magnetocaloric effect—a useful ΔT_ad in a substance exposed to a changing magnetic field—was first observed by Pierre-Ernest Weiss and Auguste Piccard in 1917 in nickel near its Curie temperature. The first application of magnetic cooling achieved temperatures below that of liquid helium (4.2 K). William Giauque and his student Duncan MacDougall’s demagnetization of a paramagnetic salt ² paved the way for subsequent investigations of materials at low temperatures and resulted in the Nobel Prize for Giauque in 1949. But no phase transition was needed for that work, whereas one is needed to observe a significant magnetocaloric effect at room temperature. That can be understood by examining the effect of a typically accessible 1-tesla magnetic field: At 300 K, the thermal energy k_BT is much larger than the magnetic energy term, μ₀MH, but with the helping hand of a spontaneous thermodynamic transition, a relatively small magnetic field can produce a large change of entropy or temperature.

Historically, the most common room-temperature magnetic refrigerant has been gadolinium. It has a large magnetic moment—from its spin angular momentum of $\raisebox{1ex}{$7$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ℏ—and a continuous, second-order, Curie disordering transition at T_c = 294 K with a field-dependent width of around 40 K; Gd’s field-induced ΔT_ad is largest around T_c. For example, ΔT_ad is about 3 K in a 1-T field at that temperature. But a useful ΔT_ad is still available at nearby temperatures, with the exact range depending on the applied magnetic field. In other words, the refrigerator engine can use efficient heat exchange at temperatures in the wings around T_c rather than precisely at T_c. The main challenge of magnetocaloric cooling is obtaining the relatively large field necessary to activate the effect; the required permanent magnets contain rare-earth elements and are expensive.

New possibilities for a magnetic refrigerator arose in 1997 with the discovery by Karl Gschneidner Jr and Vitalij Pecharsky of a “giant” magnetocaloric effect in Gd₅(Si,Ge)₄, a family of Gd alloys that has a sharp, first-order magnetostructural phase transition near room temperature, analogous to the liquid–gas transition. The new alloys have an enhanced entropic response compared with that of elemental Gd, which has a second-order transition. Subsequent materials research has addressed the optimization of entropy and temperature changes in first-order transitions. ^{3 , 4} The typical ΔS of a magnetocaloric material undergoing a first-order transition is about 10–15 J/(K kg) in a 1-T field, and the latent heat that can be extracted is as large as 30 MJ/m³.

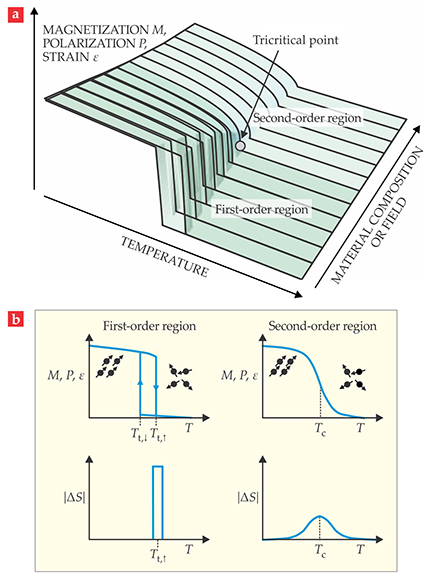
Some materials exhibit tricritical points where a first-order transition becomes second-order as a function of composition or applied field, ³ as seen in figure 2. At such a point, one can utilize the entropic benefits of the first-order transition without the punishing energy loss associated with circling the hysteresis loop: Thermal hysteresis in a second-order transition is, in principle, zero.

Electrocaloric cooling

There is a direct parallel between the response of electric polarization to a local electric field in ferroelectric materials and that of magnetization to a local magnetic field in ferromagnetic materials. That suggests that an equivalent cooling effect should exist in dielectric materials. Indeed, heat pumping with the electrocaloric effect—and its converse, the pyroelectric effect (see the article by Sidney Lang, Physics Today, August 2005, page 31 )—has been known to mankind since ancient times. Near the ferroelectric–paraelectric Curie transition temperature in an electrocaloric material, an applied electric field will line up the dipoles and release heat as the material is adiabatically placed in the lower entropy state (going from point i to point ii in figure 1c). When the field is switched off, the polarizations relax by absorbing heat (point iii to point iv).

Unlike other caloric materials, electrocalorics are primarily ceramics and polymers, and since they need to withstand applied electric fields, they are good electrical insulators. That means they are often also good thermal insulators, which can prove useful in some aspects of the heat-recovery part of the full system.

One of the first quantitative measurements of the electrocaloric effect, done in Rochelle salt, was reported in 1963 by Gordon Wiseman and Juergen Kuebler, ⁵ with a ΔT_ad of 0.003 °C. In 1981 Bruce Tuttle and David Payne reported a substantially larger 2.5 °C effect in a lead zirconate–based ceramic. ⁶

Good electrocaloric materials have a ΔS that ranges from one to tens of J/(K kg) and include common ferroelectric compounds. The heat that can be extracted from electrocalorics is in the range of tens of MJ/m³. Materials with disordered polar states are well suited for the electrocaloric effect because the disorder directly contributes to a larger entropy. Thus both special ferroelectrics called relaxors, which have intrinsic nanopolar regions, and electron-irradiated polymers, which have deliberately introduced defects that reduce coherence between individual dipoles, have been shown to display increased values of ΔS. The behavior of electric polarization is sensitive to local interfaces, so nanocomposite materials with many interfaces, widely pursued in the ferroelectric and multiferroic communities, are expected to open the door for new electrocaloric materials.

For cooling, electrocalorics typically require an electric field of 100–1000 kV/cm, comparable to their ferroelectric coercive field. For thin films on the order of 1 µm or less, the field corresponds to tens to hundreds of volts. But for some of the polymers and bulk ceramics, the voltage required for a sizable cooling effect can be a kilovolt or larger. That represents the main challenge for electrocalorics: scaling up to thicker materials. Not surprisingly, the first prototypes of electrocaloric cooling systems are small-scale devices built around multilayers—widely used structures in the ceramic capacitor industry. The initial target applications include cooling electronic devices and computers and localized climate control. ⁷

Elastocaloric cooling

As with the other caloric effects, the initial discovery of elastocaloric—and its sister, barocaloric—cooling was in nonferroic materials. It was only recently that shape-memory alloys (SMAs, which return to their original shape after deformation) were found to display a large elastocaloric cooling effect. In 1980 C. Rodriguez and L. C. Brown showed that the first-order phase transition of a copper-based SMA can be used to pump heat. ⁸ Jun Cui and his colleagues have directly measured ΔT_ad as large as 17 K using nickel–titanium wires. ⁹

Equiatomic NiTi and other SMAs undergo classic first-order transitions accompanied by significant latent heat (50–90 MJ/m³). The transition corresponds to a symmetry-lowering change in crystal structure from a high-temperature phase, known as austenite, to a low-temperature phase, called martensite. Near room temperature, that so-called martensitic transformation translates to ΔS of 10–80 J/(K kg). Martensitic metals are ductile and easily bent. Because there is a change in the lattice constant associated with the martensitic transformation, the material can develop an induced dimensional change of up to 10%. Although many crystalline materials are known to undergo martensitic transformations, not all are reversible.

The effect of elastocaloric cooling is best observed in a process essentially identical to the heating and cooling of the rubber mentioned earlier. The SMA wire in an austenitic state is placed in an environment at a temperature slightly above the transformation temperature. When the wire is pulled, it undergoes transformation into a martensite. During the transformation, the wire releases latent heat, which raises its temperature and that of its surroundings (going from point i to point ii in figure 1c). One can then hold the wire in that state until the material cools back down to ambient temperature (point ii to point iii); it is then ready to unleash its cooling power. Upon relaxing back to its unstretched state (point iii to point iv), the wire necessarily goes back to the austenite state, absorbs latent heat, and provides cooling.

A key feature of the cycle is that at point iii in figure 1c, when the wire is ready to take the path to point iv and deliver cooling, it is mechanically loaded: Much like a stretched spring, it has a stored potential energy that can be used to deliver work. Therefore, by mechanically coupling two “half-systems” moving in opposite phases of the cycle, one can devise a mechanism where unloading one half can be used to load the other half. Imagine connecting a stretched spring to an unstretched one and then letting go. The second spring will now get stretched using the stored energy from the first spring. That kind of work recovery is an important part of any cooling system based on caloric materials.

One challenge in elastocaloric cooling is to find an efficient and inexpensive way to implement cyclical mechanical force—tensile or compressive stress—so that SMA refrigerants can repeatedly and continuously undergo stress-induced transition. For a typical SMA like NiTi, the critical stresses are 400 MPa and 600 MPa for tension and compression, respectively. Although easily achievable in a laboratory setting with materials testing equipment, those values are much larger than ordinarily encountered in a household environment. It is easy to see the need to come up with clever mechanical designs and to find new compounds with much lower critical stress.

Comparing calorics

Let’s now compare materials and systems across the different caloric mechanisms. As mentioned earlier, the central figure of merit for a cooling device is the coefficient of performance, or COP. For first-order transition materials, one may also define a COP_mat as the latent heat divided by the input work required to extract that heat. In other words, COP_mat describes the efficacy of extracting the latent heat from a material. As an ultimate efficiency measure, one can then also compare COP_mat with the Carnot COP, which is given by T_c/(T_h − T_c) for a given application’s hot and cold temperatures, T_h and T_c.

A crucial material parameter is the specific heat (measured at temperatures away from the first-order transition, where it is infinite). The higher the specific heat of a refrigerant, the more heat is needed to change the temperature of the material itself, taking away from the latent heat that can be used to cool a medium. For a given temperature lift ΔT = T_h − T_c, a useful quantity is then the dimensionless latent heat γ given by the latent heat divided by the amount of heat the material consumes for self-heating or self-cooling. The higher the value of γ, the easier the heat can be imparted to the heat-exchange system. When γ is low (below about 1), an elaborate heat-exchange system is needed so that most of the latent heat is not just used to heat and cool the refrigerant itself. Figure 3 plots γ and COP_mat for various caloric materials, where the target ΔT is chosen to be 10 K.

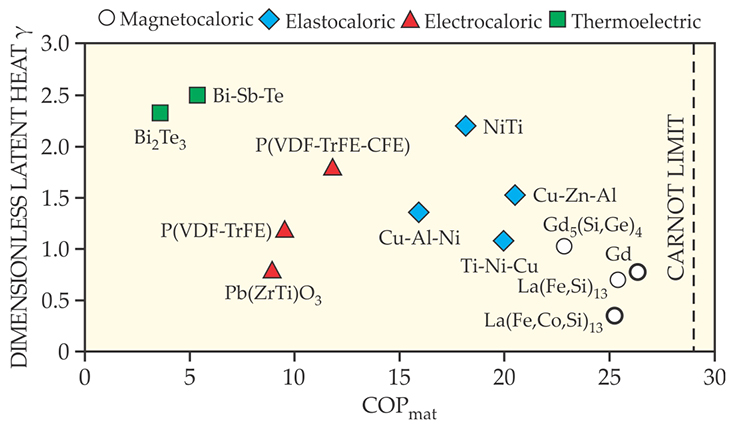
Among the three classes of caloric materials discussed here, magnetocaloric materials have the largest COP_mat, a result of the large entropy change that is attainable by a magnetic field. But their γ values are among the lowest, indicating that they need the elaborate regenerator schemes mentioned above. The COP_mat for elastocaloric materials is generally not as high as the values for magnetocaloric materials, but they have the largest γ values thanks to their low specific heats. Of the three, electrocaloric materials have the lowest recorded COP_mat, which reflects the modest latent heat values associated with their first-order transition. Electrocalorics can be considered the least developed of the three cooling technologies, and the development of high-performance electrocaloric materials is a relatively new area of research in the age-old field of ferroelectric materials.

In figure 3, we also plot some typical thermoelectric materials, which are commercially used in the Peltier cooling mechanism. For those, instead of latent heat we have used typical equivalent heat or cooling power generated in a Peltier device. The ubiquity of thermoelectric wine coolers shows the ease of harvesting sizable cooling power from a Peltier device, but thermoelectric materials are notoriously inefficient compared with caloric materials.

To extend the operational temperature range of solid-state coolers, the regenerator part of the overall system often employs various materials or fields to establish a thermal gradient along the length of the refrigerant material’s housing; when a controlled flow of heat-exchange fluid is used, different parts of the regenerator can then effectively operate at different temperatures. ¹⁰

A surge of ferroic cooling

So where are these technologies headed? Recognizing the importance of alternative cooling devices, the US and other governments have increased funding aimed at developing cooling systems based on caloric materials. Some prototype devices are shown in figure 4. In particular, the Department of Energy’s Advanced Research Projects Agency–Energy has supported projects through its Building Energy Efficiency Through Innovative Thermodevices program that have resulted in major advances for magnetic refrigeration systems and the successful demonstration of a first elastocaloric cooler. DOE’s Building Technologies Office has also recently launched several solid-state cooling projects under the Building Energy Efficiency Frontiers and Innovation Technologies program.

In Europe, governments have funded various large-scale projects—for example, Denmark has supported EnovHeat in developing magnetic heat pumps. Germany has a national six-year special priority program on ferroic cooling that funds various electro-, elasto-, and magnetocaloric research teams. European Union–supported collaborative projects include the Solid State Energy Efficient Cooling project, which has resulted in three magnetic cooling engines being built; and Drastically Reduced Use of Rare Earths in Applications of Magnetocalorics is using improvements in the magnetocaloric and heat-exchange properties of refrigerants to predict future reductions in the amount of permanent magnets required in a magnetic cooling engine.

The biggest concern manufacturers have about novel solid-state cooling is the fatigue life of caloric materials. An ordinary residential air conditioner is expected to have a 10-year life, which can mean up to several millions of operation cycles. Can caloric materials be driven back and forth millions of times through their first-order transitions? Accelerated testing of materials suggests that many of them indeed can. The key is in the hysteretic behavior of the materials as they traverse reversibly though the first-order transitions. In fact, some guiding principles are emerging for designing caloric materials with long fatigue life (see the box on page 53).

The stage is thus set to demonstrate full-scale refrigerators and air conditioners based on caloric materials. For magnetic cooling, recent prototypes by companies that include Astronautics, Camfridge, and GE Appliances have addressed various future markets such as wine coolers, domestic refrigeration, and automobile air-conditioning; the companies seek to launch commercially available products in three to five years. Elastocaloric cooling systems based on compressively stressing SMA tubes have been demonstrated, ¹¹ while Haiming Gu, Qiming Zhang, and their colleagues have constructed a multilayered chip-based electrocaloric device. ¹²

Given the intrinsically high COP of a caloric refrigerant cycle, there are reasons to be optimistic about the technologies’ commercial prospects. But there are also plenty of challenges. For novel solid-state cooling systems to be economical from an energy-saving point of view, the entire systems—not just the refrigerants—need to achieve COPs of four or higher. It remains to be seen how price-competitive complete systems will be when they first enter the commercial market. Key innovations will likely come from the intersection of materials development and system design efforts, principally through maximizing caloric effects and heat-exchange properties. If successful, solid-state cooling will surely be a highly disruptive technology.