Shape-programmable materials
DOI: 10.1063/PT.3.3051
Tailors and cartographers have long realized an ironclad mathematical truth: Objects that are curved in most ways cannot be seamlessly covered or directly represented by flat materials unless those materials are stretched or torn. For that reason, tailors need cuts and seams to make a shirt from flat pieces of cloth, and mapmakers representing Earth on a flat surface can accurately depict relative areas or local shapes but not both. A well-known consequence is the wildly out-of-proportion representation of Greenland and Antarctica in Gerardus Mercator’s well-known projection. Indeed, distorted spherical projections are known from antiquity, dating back at least as far as Ptolemy’s Planisphaerium.
Clothing a rounded form or mapping shapes and distances from a globe onto a flat sheet requires artifice or compromise, if not both. Curved and flat spaces are generically incompatible. But what if we could transcend that limitation? Imagine the possibilities for device design if we could reversibly transform a flat sheet of material into almost any shape at all. Motivated by that prospect, scientific interest in the study of origami has exploded. Already, researchers have created shape-shifting robots constructed of a series of hinged metal pieces, DNA structures that self-assemble into a multitude of three-dimensional shapes, and more. (See, for example, references and and the Quick Study by Ara Knaian, Physics Today, June 2013, page 64
Gauss’s remarkable theorem
Why are certain curved shapes so problematic? It cannot simply be a matter of having curvature—after all, gift wrap so easily accommodates a curved cylindrical shape that it is frequently sold wound around a cardboard tube. The key lies in recognizing the difference between intrinsic and extrinsic curvature. Much of our understanding of those matters is owed to the insights of 19th-century mathematical titan Carl Friedrich Gauss, pictured at right. Indeed, the most commonly encountered form of intrinsic curvature—that which occurs in 2D surfaces—bears the name Gaussian curvature.

Carl Friedrich Gauss, 1840. Portrait by Christian Albrecht Jensen.

At any point on a surface, the Gaussian curvature is the product of the two extrinsic principal curvatures, defined as the curvature of the smallest circle that fits snugly at a given point and the curvature of the snug-fitting circle that is perpendicular to the first. Here, “snug” means coinciding with the surface up to second derivatives. The curvature of a circle is the inverse of its radius.
The principal curvatures of a surface may be changed by bending or folding the surface, but their product will remain the same—so long as the surface is not stretched or compressed. That statement is Gauss’s celebrated theorema egregium, and it encodes the privileged, invariant nature of the intrinsic geometry. On a flat sheet, for example, both principal curvatures are zero at any given point. Upon bending or folding the sheet, one of the principal curvatures becomes nonzero—in fact, equal to the curvature of the bend—but the product remains zero because the sheet remains flat along the perpendicular direction. In that sense, a cylinder is flat, which is why it can be wrapped. On the other hand, the Gaussian curvature of the surface of a sphere with radius
For those of us concerned with material elasticity and mechanics, instruction comes from the exception to the invariance posited by the theorema egregium. If we want to alter the intrinsic geometry of a surface, we must stretch or compress the sheet, potentially at all locations. (See the article by Michael Marder, Robert Deegan, and Eran Sharon, Physics Today, February 2007, page 33
Exotic materials for mechanics
Ordinary materials such as paper or metal will not do if we are to realize the dream of devices that can reversibly contort and morph beyond the restrictions of their intrinsic curvature; we’ll need something new and exotic. For instance, differential growth in leaves leads to wrinkling. Isotropic swelling of N-isopropylacrylamide (NIPA) hydrogels, if engineered to vary spatially, leads to Gaussian curvature that is reversible on deswelling. In this article we review continuing developments in NIPA hydrogels. But we also turn to liquid-crystal solids, which undergo remarkably large shape changes beyond simple volume change.
A liquid crystal in the so-called nematic phase has the long axis of its rod-like molecules correlated with a direction called the director. Thus nematics are anisotropic liquids with directional but not spatial order. In materials called liquid-crystal solids, the nematics reside on long, chain-like polymer molecules. Cross-linking between chains forms a network that then becomes a solid rather than a flowing liquid of polymer chains. In those polymeric nematic solids, the liquid-crystal rods bias the otherwise random configurations of the long-chain backbones, as illustrated in figure 1a, so that the chains are stretched out along the nematic director and contracted in the perpendicular directions. The solid that the chains make up exhibits its own corresponding mechanical elongation.

Figure 1. It’s a stretch. In its nematic phase (a), the constituent liquid-crystal rods of a liquid-crystal elastomer are orientationally ordered about a preferred direction n, the director. As a result, the random walk of the elastomer’s polymers is also biased along the director. The orange dots represent cross-links between chains that frustrate flow and make the elastomer a solid. (b) Upon heating, the length of the nematic block decreases and the width increases. Eventually the material becomes isotropic.
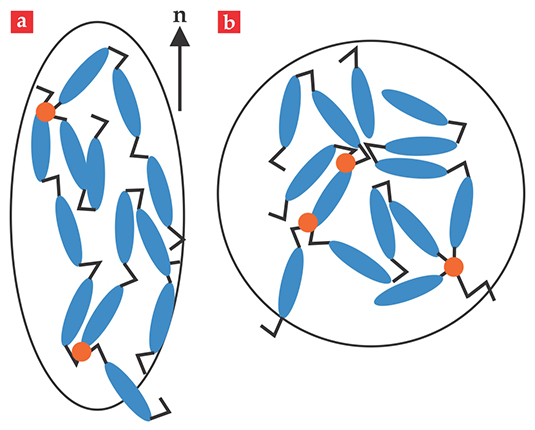
A sparse cross-linking of the polymer chains yields an elastomer—a soft, rubbery solid in which the local molecular environment remains liquid-like. If the nematic elastomer has a uniform director, then a block of elastomer will be longer along the nematic direction and shorter along the perpendiculars than it would be in the isotropic phase. Heating such a block reduces the nematic order—that is, the extent of molecular alignment. As a result, the substance shortens along the nematic director and elongates in the perpendicular directions. Eventually the block becomes isotropic, as illustrated in figure 1b. Cooling reverses the length transformations and restores the original, biased shape.
Remarkable strains can be achieved in liquid-crystal elastomers. Cooling drives extensions to as much as four times the original length, and heating gives recovery. Other external control is possible. For instance, if as little as 5% of the molecular rods are dye molecules that bend on illumination, then light can strongly reduce nematic order, since bent rods do not pack nearly as effectively. Hence light can cause mechanical contractions analogous to the thermal heating response just discussed. In the dark, the solid recovers and elongates, just as it does when cooling follows a heating step.
Preparing a NIPA hydrogel involves mixing NIPA and a bisacrylamide cross-linker in water. The hydrogels have a sharp shrinkage transition at a critical solution temperature of about 33 °C. Below the critical temperature, the polymer molecules are strongly repulsive and the gel is accordingly swollen. As the transition temperature is exceeded, the intermolecular interaction becomes attractive, water is expelled from the gel matrix, and the gel collapses to as little as 1/10 its original size. The total amount of shrinkage (or swelling, when the transition temperature is crossed from above) depends on the specific concentration of NIPA and the strengths of the intermolecular interactions above and below the critical temperature. Note that in contrast to the uniaxial deformations of the liquid-crystal solids, the local swelling or shrinking in NIPA hydrogels is isotropic.
Buckling out of a plane
To this point we have described novel materials whose local dimensions can change in a coherent way. Is that capacity for change enough to bridge the gap to real shape programmability? Is it possible to seamlessly wrap at least parts of a sphere with a flat sheet of one of those materials? Clearly, spatially homogeneous deformations alone are not good enough. A flat sheet of a liquid-crystal solid with a uniform director will extend in one direction and shrink in the other, but it will remain a flat sheet. For a sheet of uniform hydrogel, the extension will be constant in all directions, but the result is again a flat sheet, albeit one with a different volume.
If shape programmability is to be achieved, spatial inhomogeneity must somehow be introduced to the local changes of dimension. Consider a thin sheet of liquid-crystal solid in which, as illustrated in figure 2a, the director pattern is simply concentric circles. In the liquid-crystal business, in two dimensions, that pattern is called an azimuthal +1 disclination defect. When the sheet is heated, the material shrinks along the concentric circles, which are everywhere tangent to the nematic director. At the same time, the material elongates in the radial direction, because that direction is everywhere perpendicular to the director field. A geometric crisis arises since the ratios of circumferences to corresponding radii are now less than the familiar
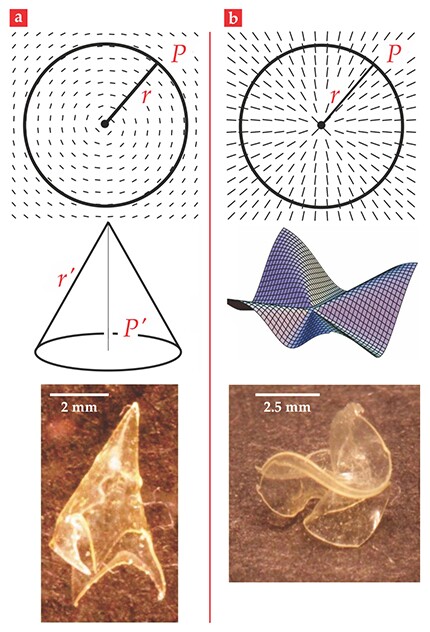
Figure 2. Cones and anti-cones from flat sheets. (a) When a flat liquid-crystal solid with a concentric, circular pattern of directors (top) is heated, it pops into a cone (middle). The bottom image shows an experimental realization. (b) When the director pattern is radial (top), heating causes the sheet to buckle into an anti-cone (middle). The bottom image shows an experimental realization. The indicated geometric parameters are discussed in the text. (Photographs courtesy of Timothy White.)
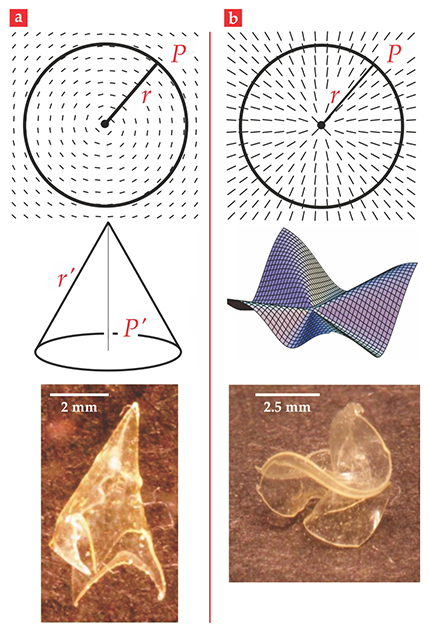
In figure 2a we have indicated a circle with circumference
After deformation, the perimeter-to-radius ratio becomes
In figure 2b, the director pattern on a flat sheet is radial—a radial +1 disclination defect. When the sheet is heated,
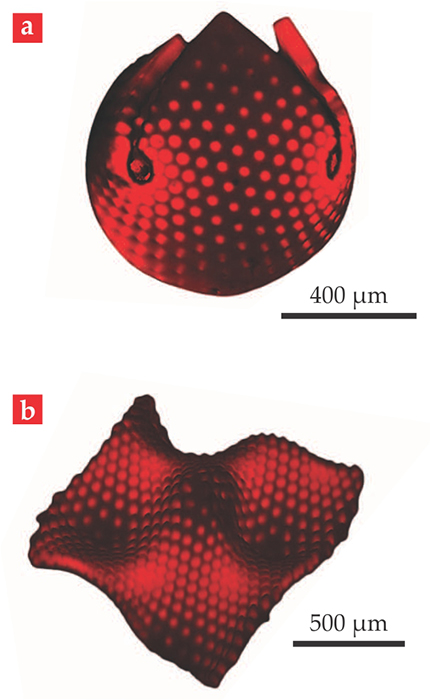
Spatial inhomogeneities can be created in NIPA hydrogels by varying the local concentration of NIPA in the course of preparing the gel (see reference and Physics Today, May 2012, page 15

Figure 3. Contorting hydrogels. N-isopropylacrylamide (NIPA) hydrogels swell when cooled below a specific transition temperature. With appropriately chosen concentration gradients, a NIPA hydrogel can be induced to swell into such shapes as (a) a sphere and (b) a ruffled surface. (Adapted from ref.
A toolkit for device design
Physicists now face the challenge to move beyond the ideas of the previous section and leverage them to achieve programmable, switchable shapes for practical device design. Before we address that challenge head on, we note that from the point of view of the intrinsic geometry, a smooth cone is indistinguishable from a polyhedral corner. The corners of a closed book, the corners of a box, and the sharp, jutting end of the coffee table that devils your shins are all cones. The difference between the polyhedral corner and the cone lies purely in the extrinsic geometry of folding: The surface around the polyhedral corners has distinct ridge lines—folds or creases—but the smooth cone does not.
Anti-cones, too, correspond to many familiar examples with distinct ridge lines and otherwise flat regions, such as the joint between a chimney and a roof. But in those cases the polyhedral regions have anti-corners, regions where you must traverse more than
Recent advances in the preparation and writing of custom director fields have opened the door to working with nearly arbitrary patterns. 11 However, one still needs to stitch together regions with different “textures,” or liquid-crystal orientations. The task is a nontrivial one, as the boundaries for isolated defects are generally incompatible and the geometry that results from the smoothed-out, energy-minimizing texture is generically nowhere flat—and thus does not produce polyhedral corners. It turns out, however, that simple wedges and triangles of uniform, azimuthal, or radial textures may be used as building blocks, provided those wedges are pieced together according to appropriate rules: The director field must either be constant across a join, or the wedges’ director fields must meet at a rank-1 connected boundary, meaning that the angle to the boundary is the same on both sides.
Figure 4a shows examples of building-block wedges. The change in angular extent of any such wedge as a function of the spontaneous strain is easy to calculate. So, given a collection of unstrained wedges that fill all the space around a point, it is straightforward to determine whether the strained system produces a new total angle that is greater or less than
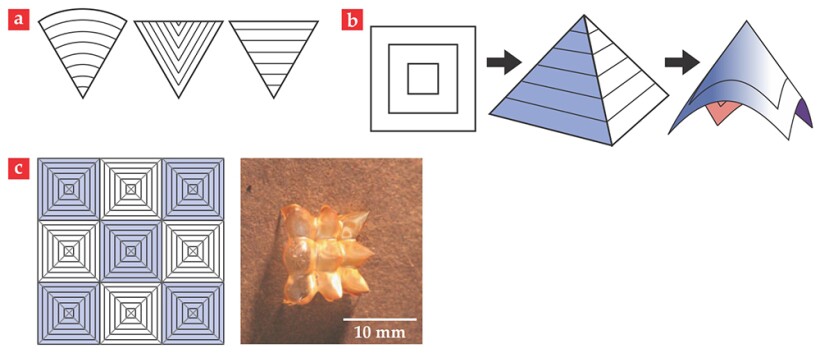
Figure 4. Building blocks for shape programming. (a) The straight lines in these wedges represent liquid-crystal director patterns. When combined according to rules described in the text, such wedges can be the building blocks of shape-programmable materials. (b) A concentric-square director pattern built from four building-block wedges deforms into a square pyramid when the liquid crystals along the directors contract. The pyramid then relaxes to a smooth cone. (c) This array of concentric squares explicitly shows the 36 building-block wedges. It deforms into an array of square pyramids that cannot relax to their smooth conical form because the stretch-energy cost for doing so is too great. The array in the photograph (adapted from ref.
When pyramids meet
We next turn to two simple examples that convey an idea of the shapes and textures that can be created using the wedge-joining methodology. First, imagine a sheet whose director pattern is a set of concentric squares, as in figure 4b. Such a sheet will behave under heating just as the azimuthal +1 disclination defect described earlier, though with a somewhat weaker response to the spontaneous strain. Notably, the resulting shape is not the creased pyramid one might expect; instead, the result is a cone, created as the pyramid relaxes its bend energy and smooths out.
Now imagine a large sheet with many copies of those concentric-square textures. 12 As figure 4c illustrates, that simple tiling obeys the rules of the wedge joining. Moreover, in addition to the +1 azimuthal disclination defects at the centers of the concentric squares, the tiling also has locations that behave like +1 radial disclination defects (experts will recognize them as negatively charged −1 disclinations) where four corners of the original squares join. Those locations should transform into anti-cones if the sheet is heated, so the shape formed by the sheet upon heating is not simply the iterated solution of the isolated square tile—an array of smooth cones. Indeed, two neighboring smooth cones would intersect on a parabola curving away from the conical tips, but all along that parabola, the material bending perpendicular to the parabola would curve toward the tips. As a result, the Gaussian curvature is negative along the parabola.
The appearance of Gaussian curvature where the natural geometry does not demand it means a costly stretch. The material, in fact, does not pay the price. Instead, at the cost of incurring some extra but relatively cheap bend energy, the would-be cones remain the creased pyramids with polyhedral corners that they were before relaxing. The neighboring pyramids meet along flat lines, and there is no longer Gaussian curvature where there shouldn’t be. As we describe below, such pyramidal arrays can be used in devices that support weight or pump liquids.
Our second example is also directly tailored to a device application. The ability of a flat sheet to reversibly and controllably fold up and completely encapsulate a volume would be desirable for many purposes, including drug delivery and micro- or nanoscale mechanical transport. Imagine a texture similar to the concentric squares, but instead using concentric equilateral triangles. Now take four such equilateral triangles and join them to form one larger equilateral triangle, as illustrated in figure 5a. As the large triangle of material is heated or illuminated, four pyramids rise up from the four triangular patches. To reduce any energy of creasing between the pyramids, the material conspires to produce flat surfaces between the central and outer pyramids. Creases only develop along the rank-1 boundaries in the individual triangular patches, as seen in figures 5b and 5c. Eventually, the material from the corners of the large triangle is pushed so far around behind the central patch that the outer pyramids meet behind the central one. At the moment of their meeting, the sheet has closed itself into a cube.
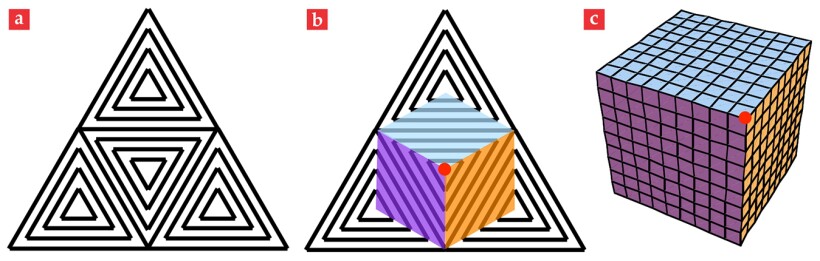
Figure 5. A programmable enclosure. Four concentric equilateral-triangle director patterns combine to give the large triangular pattern depicted in (a). When liquid crystals contract along the director pattern, a pyramid pops out from each small triangle; eventually those pyramids close onto a cube. (b) The colored regions and red dot on the large triangle become the correspondingly colored cubical faces and indicated vertex in the cube depicted in (c). The grid pattern on the cube emphasizes the three-dimensional nature of the shape.
The alternative to stitching together evolving polyhedra would be, given a desired target shape, to find the corresponding distribution of Gaussian curvature and then seed that distribution through prescribed director fields or NIPA concentrations. That difficult problem remains open, though the tools of differential geometry have allowed it to be at least partially addressed: Theoretical work has established that director fields can be determined for rather general distributions of Gaussian curvature. 13–15 Finding the surface that corresponds to a specified distribution of curvature remains a difficult challenge that may not even have a unique solution since the bending a surface undergoes to minimize its bend energy does not change Gaussian curvature.
Getting to work
Now is an exciting time to be exploring shape programmability, thanks to the confluence of, first, recent laboratory advances in the production of new, exotic materials that can change their local dimensions and, second, theoretical insights about the interplay between Gaussian curvature and elasticity. We in the field are continuing to refine material techniques, extend our ability to fully model the elastic energetics of shape-shifting systems, and cleanly prescribe an exact director field or concentration gradient to achieve a specific, desired shape.
Several common themes emerge when considering the requirements for a shape-shifting device. First, to be effective, actuation must involve stretch—which is strong—rather than much weaker bends. Gaussian curvature is the perfect route to usable stretch, as may be seen by returning to the array of rising square pyramids shown in figure 4c. The pyramids in the array rise to avoid stretch energy in the face of a changing internal geometry. Accordingly, if the movement to the new shape were frustrated—for instance, if a heavy plate were placed on the array sheet before heating or illumination, then stretch would result and a strong force would act. Indeed, Timothy White and colleagues, who created the array in figure 4c, 11 found that a smaller array of four pyramids could lift a mass about 150 times that of the original sheet. Forces can also develop if a shape-shifting stimulus is removed. Consider a plate that has adopted a new shape in response to a stimulus and imagine that fluid flows underneath it. Upon removal of the stimulus, large stretches develop if the plate is impeded in its return to planarity. The enclosed liquid is vigorously pumped out of the way, and, again, work is done.
Second, shapes such as lenses, which exploit their curvature, can be dialed up from complex but smooth director patterns. Third, in most devices that would make use of shape-shifting materials, the shape-changing component needs to be anchored to a surrounding, unchanging medium. Encapsulation applications are the exception, but a lifter or a pump must be incorporated into a structure. And that need leads to a problem of great subtlety that is currently being addressed: How can one have a substance that changes drastically but doesn’t change along the line of contact with its surroundings?
Shape programmability is approaching the point where device design is limited only by the imagination and creativity of the designer. Myriad avenues to effective soft devices are open. Drug delivery and encapsulation methods, peristaltic pumps and gateway switching for lab-on-a-chip microfluidics, repeatedly flushable sieves for large chemical or colloidal reaction chambers, dynamically controllable surface bumpiness for modulating aerodynamic effects on a wing, morphable digital displays of Braille for the blind, haptic feedback for touch screens, switchable and transformable gears, and even “photomechanical” cells in which energy is stored in intrinsic geometry are just a few of the possible practical applications of shape programmability. All those and more are now within reach.
In a wonderful adaption of the words of Marshall McLuhan, Kaushik Bhattacharya and Richard James said, “The material is the machine.” 16 All the ambitious applications just listed are achieved not with complicated, constructed machines but by means of monolithic programmed materials that are themselves the machines. It is a marvelous way to proceed at small length scales.
References
1. S. Felton et al., Science 345, 644 (2014). https://doi.org/10.1126/science.1252610
2. D. Han et al., Science 332, 342 (2011). https://doi.org/10.1126/science.1202998
3. E. Sharon, E. Efrati, Soft Matter 6, 5693 (2010). https://doi.org/10.1039/c0sm00479k
4. J. Dervaux, M. Ben Amar, Phys. Rev. Lett. 101, 068101 (2008). https://doi.org/10.1103/PhysRevLett.101.068101
5. M. M. Müller, M. Ben Amar, J. Guven, Phys. Rev. Lett. 101, 156104 (2008). https://doi.org/10.1103/PhysRevLett.101.156104
6. C. D. Modes, K. Bhattacharya, M. Warner, Proc. Roy. Soc. A 467, 1121 (2011). https://doi.org/10.1098/rspa.2010.0352
7. L. T. de Haan et al., Angew. Chem. Int. Ed. 51, 12469 (2012). https://doi.org/10.1002/anie.201205964
8. C. D. Modes, M. Warner, Phys. Rev. E 92, 010401–R (2015).https://doi.org/10.1103/PhysRevE.92.010401
9. J. Kim et al., Science 335, 1201 (2012). https://doi.org/10.1126/science.1215309
10. J. Kim et al., Soft Matter 8, 2375 (2012). https://doi.org/10.1039/c2sm06681e
11. T. H. Ware et al., Science 347, 982 (2015). https://doi.org/10.1126/science.1261019
12. C. D. Modes, M. Warner, Phys. Rev. E 84, 021711 (2011). https://doi.org/10.1103/PhysRevE.84.021711
13. Y. Klein, E. Efrati, E. Sharon, Science 315, 1116 (2007). https://doi.org/10.1126/science.1135994
14. H. Aharoni, E. Sharon, R. Kupferman, Phys. Rev. Lett. 113, 257801 (2014). https://doi.org/10.1103/PhysRevLett.113.257801
15. C. Mostajeran, Phys. Rev. E 91, 062405 (2015). https://doi.org/10.1103/PhysRevE.91.062405
16. K. Bhattacharya, R. D. James, Science 307, 53 (2005). https://doi.org/10.1126/science.1100892
More about the Authors
Carl Modes is a postdoctoral associate at the Rockefeller University in New York City. Mark Warner is a professor of physics at the University of Cambridge in Cambridge, UK.






