Roaming reactions: The third way

Much of what is known about chemical-reaction dynamics comes from looking at the decomposition of isolated hot molecules whose energies can be precisely controlled. Those unimolecular reactions can offer insight that’s applicable to the more familiar bimolecular reactions, but without the complications of having to account for the impact parameter and relative orientation of two reacting molecules. As a result, it is possible to study relatively large systems at a level of detail not available with bimolecular methods.

Chemists have long assumed that unimolecular dissociation follows one of two decomposition modalities. The first is dissociation over a potential energy barrier into a pair of smaller molecules, as shown in figure 1a. The barrier arises because of the rearrangement of electrons in breaking old bonds and forming new ones. The second dissociation modality involves simply stretching a bond until it breaks, as shown in figure 1b. The dissociation typically gives rise to a pair of fragments called radicals, highly reactive species that are electrically neutral and have unpaired electrons. Because no new bonds are formed, the energy necessary to form the products is just the difference in energy between the products and the reactant molecule, with no additional barrier. Sufficiently large molecules may have many dissociation pathways of each type; widely used theories describing the pathways assume that they are independent and noninteracting.

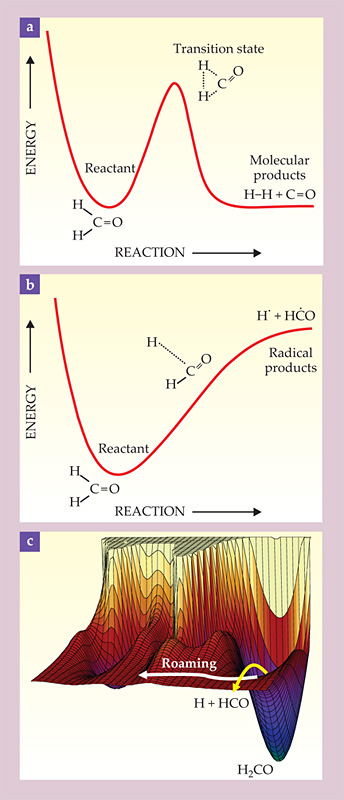
However, theoretical and experimental work during the past few years has led to the discovery of a third, complex decomposition pathway called “roaming.” The roaming pathway starts off in the direction of the second dissociation modality, as shown in figure 1c, with the stretching of a single bond. But it winds up in the first modality, with the formation of molecular products, or possibly even in a different, distinct modality. Roaming is now widely assumed to be quite general. Its discovery raises significant challenges to the theoretical description of chemical reactions and may have practical implications across a range of disciplines.

Foundations

Essential to an understanding of roaming, and guiding the chemical intuition of theorists and experimentalists alike, is the notion of the potential energy hypersurface, or potential energy surface (PES) for short: the idea that every configuration of a molecule’s atomic nuclei is associated with a single (ground-state) electronic energy. (The famous and fundamental Born–Oppenheimer approximation implies that the electrons can instantaneously adjust to any change in nuclear configuration.) For a two-atom molecule, configuration space is one-dimensional, and the potential energy is a function of the internuclear distance alone. For a triatomic system, the potential energy depends on three coordinates; two internuclear distances and an angle might be a suitable choice. For a four-atom system, six coordinates are required, and so on. (It’s often useful to visualize a high-dimensional PES in two variables, as in figure 1c.)

The global minimum of a molecule’s PES is its equilibrium geometry. However, quantum mechanics tells us that the molecule cannot sit at that geometry but instead must execute at least zero-point motions. A highly energized molecule executes a large-amplitude motion, which ultimately determines how the molecule decomposes. The accurate determination and mathematical representation of the PES constitute a large and active area of research, essentially the domain of electronic structure theory and computation. (See the article by Martin Head-Gordon and Emilio Artacho in PHYSICS TODAY, April 2008, page 58 .)

Describing a decomposing molecule quantum mechanically requires propagating its wavefunction on the PES, a task that is computationally beyond reach for molecules with more than three atoms. Computing the trajectories classically or quasi-classically is more feasible but still computationally demanding and, like the quantum approach, it does require the full PES, which is itself a challenge to obtain.

There has thus been a need for more approximate approaches to describe the reactions. Of those, transition state theory (TST), developed in the 1930s ^{1 , 2} (long before computers were available), is one that has stood the test of time. The basic notion behind TST is the existence of a bottleneck, or transition state (TS), for any reaction channel, so that the reaction rate can be determined by the rate through the TS. For dissociation over a barrier, the TS corresponds to the peak of the barrier, a saddle point on the PES. More recently, TST has been extended to describe barrierless dissociations. ^{3 , 4} The TS bottleneck is a real phase-space restriction, not an imaginary construct: Intuitively, the rate of traffic flow through a mountain pass depends on the width of the pass. In a widely used hybrid TST–dynamics method, molecular trajectories are initiated at the TS bottleneck rather than at the PES minimum.

Closely related to TST, and now an inseparable extension of it, is the concept of the intrinsic reaction coordinate (IRC). ^{5 , 6} The IRC is the minimum-energy path that smoothly connects reactants to products by way of the TS. Knowing the potential energy along and around the IRC allows important dynamical extensions of TST, including various treatments of tunneling, curvature effects, and corner-cutting, and culminating in the so-called reaction path Hamiltonian treatment. ⁷ Henceforth in this article, TST will refer to TST with the associated IRC.

The information required to apply TST is the potential along the IRC and, generally, a fairly small region around it—just a small slice of the full PES. Indeed, that is what makes TST such a powerful and useful treatment: Vast regions of the molecular configuration space become irrelevant, and one need only know the properties of a local, isolated region. At least that is the assumption of TST.

Formaldehyde anomalies

The first published use of the term “roaming” to describe a type of chemical reaction was in a 2004 Science paper, ⁸ in which the two of us and others conclusively explained some anomalous results first reported in a 1993 paper by C. Bradley Moore’s group at the University of California, Berkeley. ⁹ Moore and coworkers were studying dissociation of formaldehyde (H₂CO) into H₂ + CO, with particular attention to the rotational energy imparted to the CO products. When they excited the H₂CO molecules to relatively low energy—just enough to form H₂ + CO but not enough to form H + HCO—the CO rotational distribution peaked sharply around a high rotational energy: about 45 quanta. That result was consistent with dissociation through a tight TS—a narrow mountain pass. The recoiling H₂ fragment would push against the C atom to set the CO fragment spinning, and the narrowness of the bottleneck would constrain all the dissociating molecules to follow nearly the same trajectory, thus giving all the CO molecules the same rotational kick.

But when Moore and colleagues excited the H₂CO molecules with slightly more energy, above the threshold to form H + HCO, a shoulder appeared on the low-energy side of the CO rotational distribution, an observation for which TST provided no obvious explanation. Moore and Roger van Zee proposed two possibilities. One, more favored, suggested that the anomaly was due to some as yet undefined interaction between the H + HCO radical pathway and the H₂ + CO molecular pathway. A second intriguing possibility was “extreme anharmonicity of the TS”: The TS might start out as a narrow mountain pass but quickly broaden at higher energies, so that higher-energy molecules might dissociate from geometries far from the known saddle point.

In a loose sense, both of those explanations have some merit: As quasi-classical trajectory calculations would later show, the TS anharmonicity arises from the presence of the radical pathway and is responsible for the anomalous low rotational levels of CO.

State selection

A new level of insight into the H₂CO results came from a novel experimental technique called high-resolution state-selected ion imaging, ¹⁰ with the latest improvements: velocity mapping and DC slice imaging. In those experiments, one spectroscopically selects a particular CO rotational and vibrational state and collects a 2D image of all the fragments in that state. The image is a map of the CO molecules’ velocities: The slowest fragments show up nearest the center, and the fastest ones appear farthest away. Momentum and energy conservation then dictate the corresponding H₂ internal-state distribution: The CO momentum uniquely determines the H₂ momentum, and whatever energy is left over must be H₂ internal (vibrational and rotational) energy. An advantage in the H₂CO system is that the quantum states of H₂ are widely spaced, making it easier to assign particular CO signals to the states of the H₂ partner fragments.

Figure 2 shows three different sliced velocity-map images obtained for different CO rotational levels. Figure 2a is for a high rotational energy, 40 quanta. As the image shows, CO fragments created with that much rotational energy also have high translational energy, with little energy left for H₂ internal energy. (The thin rings correspond to H₂ partner fragments in vibrational states 0 through 4.) All of those observations are consistent with the long-established mechanism of dissociation over a tight TS.

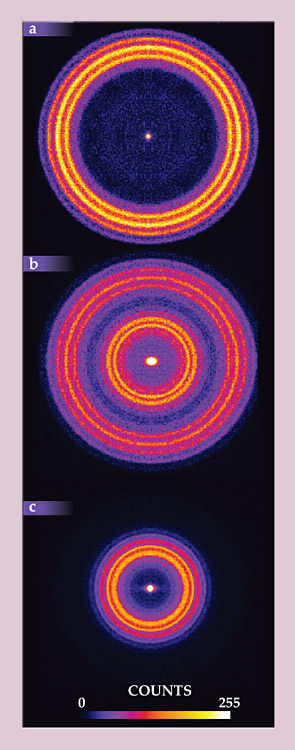
But in figures 2b and 2c, for CO with 28 and 15 rotational quanta, respectively, the story changes. At least some of the CO created with less rotational energy also has less translational energy. The H₂ partner fragments must therefore be highly vibrationally excited, with up to 8 quanta (about 4 eV) of vibrational energy. There is no reasonable way to explain how such highly excited H₂ fragments could be formed by dissociation over the familiar TS, because no such dissociation trajectory could stretch or compress the H₂ that much. The unexplained H₂ excitation, combined with the bimodal distribution in figure 2b, clearly suggests two different reaction mechanisms in play. We must now turn to theory for a plausible interpretation.

A look at roaming

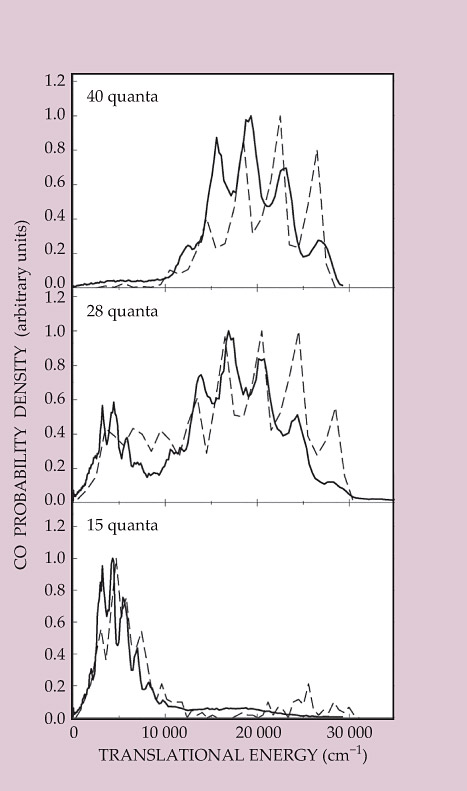
Like experimental methods, theoretical capabilities have come a long way since Moore’s 1993 paper. Methods for computing the energy of any configuration of nuclei have become quicker and more accurate, and have led to the development of a global PES for H₂CO that extends far beyond the small slice needed for TST. Hundreds of thousands of quasi-classical trajectories were calculated using that PES, starting at the H₂CO equilibrium structure and following through to the dissociation products, and their outcomes were collected and compared to experiment. Figure 3 shows some of the results: translational energy distributions for the same CO states shown in figure 2. In agreement with experiment, the theory shows the same slow molecular products with vibrationally excited H₂.

One great advantage of the computed trajectories is that they can be slowed by a factor of 10¹² or more, so that we can track the motions of individual atoms in a way that experiment does not allow. (Animations of a few H₂CO trajectories are included in the online version of this article.) In addition to the conventional over-the-barrier pathway to yield H₂ + CO and the simple bond fission into H + HCO, the trajectories revealed an alternative third pathway, which gave the molecular products H₂ + CO. In the alternative pathway, one C–H bond began to stretch, and the molecule nearly dissociated into the radicals H + HCO, but before the bond could break, the H atom began roaming around the HCO fragment at a large distance, giving rise to an intramolecular radical–radical reaction. A true radical–radical reaction (a free H atom colliding with an HCO radical to give H₂ + CO) is highly exoergic and is well known to yield high vibrational excitation in the new (H–H) bond, because the reaction takes place at long range with the new bond highly stretched. It’s not a surprise, therefore, that the roaming pathway also yields vibrationally excited H₂. In figure 4, snapshots of one roaming trajectory illustrate the process.

A different way of visualizing the trajectories, developed by Frank Suits at the IBM Thomas J. Watson Research Center, is shown in figure 5. Figures 5a, 5b, and 5c show the paths of the two H atoms over several hundred time steps prior to dissociation, and figures 5d, 5e, and 5f show the potential energy and the two C–H distances for the same trajectories over the same period. Figure 5a is a conventional trajectory leading to vibrationally cold H₂, and figures 5b and 5c are roaming trajectories.

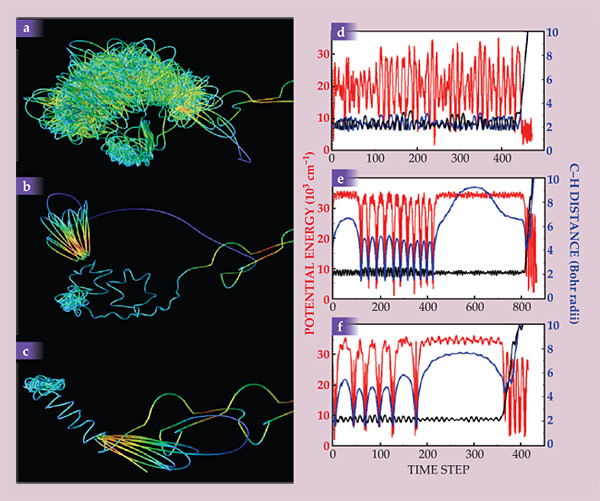
In the conventional trajectory, the H atoms move seemingly at random, and neither strays far from the C atom. The potential energy fluctuates wildly, because the vibrations in the many modes of the molecule are uncorrelated. In the roaming trajectories, one H atom pulls far away from the C atom, moves slowly around the molecule, and finally approaches the other atom for reaction. While the atom is roaming, the potential energy remains high, nearly reaching the total available energy, as it would if the molecule actually underwent dissociation into radicals. The roaming H atom can fall back in, undergo additional large-amplitude C–H vibrations, and then emerge again to roam. The reaction appears to occur at C–H distances of 5–6 Bohr radii (3–4 Å) and at a long enough H–H distance to vibrationally excite the newly formed H₂ molecule.

New insight

For all the answers the theoretical studies provided, they raised many more questions. Is it only H atoms, with their characteristic large-amplitude motion, that exhibit roaming behavior, or can other radicals also roam? Does roaming occur only at energies near the radical dissociation threshold? If not, what is its energy dependence and why? Can the roaming pathway be reconciled with TST, even though it appears not to have a conventional saddle point at all? Above all, is roaming a curiosity of formaldehyde, or is it a more general phenomenon?

A question that frequently arose when viewers watched the roaming trajectories was “Why doesn’t it just dissociate?” The answer actually holds an insight into roaming dynamics that perhaps could have been anticipated long ago. Modern statistical TST tells us that in order to break a bond, vibrational energy in excess of the bond energy must accumulate in that bond. For a polyatomic molecule in which vibrational energy flows randomly among many vibrational modes, the buildup of enough energy in one bond is an unlikely event. Excited molecules with energies well above the dissociation threshold may therefore persist for nanoseconds or microseconds—countless oscillations of the bond that ultimately breaks—before dissociation occurs. It is somewhat less rare for almost enough energy to accumulate in that bond—and for roaming to long range to occur. As the bond is stretched, it can become floppier—the bond angles are no longer so tightly constrained—and the system may explore large regions of configuration space, which may lead to alternative reactive sites. Rather than “Why roaming?” the question really should be “Why not roaming?” How has the ubiquitous third way been overlooked for so long? The oversight reflects on the limitations of our experimental methods, our impatience with computing long trajectories, and even perhaps the inadequacy of our imagination. It is a lesson in humility.

Other systems

We have learned much about roaming since the formaldehyde experiments. Experiments on acetaldehyde (CH₃CHO, similar to formaldehyde but with one more C atom) indicate roaming in its molecular dissociation (to CH₄ + CO) as well. ^{11 , 12} The experiments have stimulated further theoretical work on acetaldehyde dissociation ^{12 , 13} (confirming roaming) and theoretical and experimental work on the thermal decomposition of acetaldehyde. ¹⁴ It is now clear that roaming is the dominant dissociation pathway for excitation energies near and just below the threshold for dissociation into radical products. Above that threshold, the radical dissociation dominates, since it has a looser transition state—a wider mountain pass—than the normal molecular pathway. In fact, the roaming reaction may be viewed as a distinct pathway to molecular products, a pathway that is derived from the radical channel and that opens at a small window below each radical product state.

Roaming is actually a striking example of a broader class of intriguing, newly recognized chemical behavior: dynamically controlled reactions, or non-minimum-energy-path reactions, in which the reaction trajectories do not follow simple paths between minima on the PES but instead follow distinct pathways determined dynamically. ^{13 , 15 , 16} Like roaming reactions, dynamically controlled reactions can also give rise to unanticipated internal state distributions or products that TST cannot easily accommodate.

In addition to formaldehyde and acetaldehyde, roaming has been characterized in molecular beam experiments ¹⁷ on NO₃ and in a range of shock-tube studies under combustion conditions for systems including a variety of alkanes. Roaming-mediated isomerization of nitromethane (CH₃NO₂) to methyl nitrite (CH₃ONO) explained a long-standing anomaly in the yield of NO from CH₃NO₂ dissociation. Roaming-mediated isomerization to the nitrite, which then loses NO, may be a dominant theme in the decomposition of nitro compounds. Many more examples have been examined theoretically. Experimental studies have lagged somewhat behind, because probe strategies that can isolate the roaming signatures (highly excited new bonds, bimodal distributions of quantum states) are much more difficult to achieve or show convincingly for large polyatomic molecules. One open question is what role the roaming TS, if there is one, plays in determining roaming rates. Another concerns the precise relationship between the roaming region on the PES and the normal TS region. How well separated are they? Those are questions of keen interest and active research.

Many researchers now realize that roaming is an important, long-overlooked mechanism of unimolecular dissociation: a distinct third pathway to molecular products that benefits from the presence of the radical channel. The implications of overlooked roaming events are now actively being investigated for their impact on atmospheric, combustion, and planetary chemistry.

Supplemental material

Animated simulations of formaldehyde dissociation

Conventional dissociation to molecular products, H₂ + CO

Dissociation to radical products, H + HCO

Roaming reaction to molecular products

Roaming reaction from the point of view of the roaming atom

To view additional simulations, visit Joel Bowman’s H₂CO page .