Reversing Light With Negative Refraction

Victor Veselago, in a paper ¹ published in 1968, pondered the consequences for electromagnetic waves interacting with a hypothetical material for which both the electric permittivity ∊ and the magnetic permeability µ were simultaneously negative. Because no naturally occurring material or compound has ever been demonstrated with negative ∊ and µ, Veselago wondered whether this apparent asymmetry in material properties was just happenstance or perhaps had a more fundamental origin. He concluded that not only should such materials be possible, but if ever found, they would exhibit remarkable properties unlike those of any known materials and would give a twist to virtually all electromagnetic phenomena. Foremost among these properties is a negative index of refraction.

Veselago always referred to the materials as “left handed,” because the wave vector is antiparallel to the usual right-handed cross product of the electric and magnetic fields. We prefer the negative-index description. The names mean the same thing, but our description appeals more to everyday intuition and is less likely to be confused with chirality, an entirely different phenomenon.

Why are there no materials with negative ∊ and µ? One first needs to understand what it means to have a negative ∊ or µ and how negative values occur in materials. The Drude-Lorentz model of a material is a good starting point, because it conceptually replaces the atoms and molecules of a real material by a set of harmonically bound electron oscillators resonant at some frequency ω ₀. At frequencies far below ω ₀, an applied electric field displaces the electrons from the positive cores and induces a polarization in the same direction as the applied field. At frequencies near resonance, the induced polarization becomes very large, as is typical in resonance phenomena; the large response represents accumulation of energy over many cycles, such that a considerable amount of energy is stored in the resonator (in this case, the medium) relative to the driving field. So large is this stored energy that even changing the sign of the applied electric field has little effect on the polarization near resonance! That is, as the frequency of the driving electric field is swept through the resonance, the polarization flips from in-phase to out-of-phase with the driving field, and the material exhibits a negative response. If instead of electrons the material response were due to harmonically bound magnetic moments, then a negative magnetic response would exist.

Although somewhat less common than positive materials, negative materials are nevertheless easy to find. Materials with negative ∊ include metals (such as silver, gold, and aluminum) at optical frequencies; materials with negative µ include resonant ferromagnetic or antiferromagnetic systems.

That negative material parameters occur near a resonance has two important consequences. First, negative material parameters will exhibit frequency dispersion: They will vary as a function of frequency. Second, the usable bandwidth of negative materials will be relatively narrow compared with positive materials. These consequences can help answer our initial question as to why materials with ∊ and µ both negative are not readily found. In existing materials, the resonances that give rise to electric polarizations typically occur at very high frequencies—in the optical for metals, and at least in the terahertz-to-IR region for semiconductors and insulators. On the other hand, resonances in magnetic systems typically occur at much lower frequencies and usually tail off toward the THz and IR region. In short, the fundamental electronic and magnetic processes that give rise to resonant phenomena in materials simply do not occur at the same frequencies, although no physical law would preclude such overlap.

Metamaterials extend material response

Because of the seeming separation in frequency between electric and magnetic resonant phenomena, Veselago’s analysis of materials with ∊ and µ both negative might have remained a curious exercise in electromagnetic theory. However, in the mid-1990s, researchers began looking into the possibility of engineering artificial materials to have a tailored electromagnetic response. Although the field of artificial materials dates back to the 1940s, advances in fabrication and computation—coupled with the emerging awareness of the importance of negative materials—led to a resurgence of effort in developing new structures with novel material properties.

To form an artificial material, we start with a collection of repeated elements designed to have a strong response to applied electromagnetic fields. As long as the size and spacing of the elements are much smaller than the electromagnetic wavelengths of interest, incident radiation cannot distinguish the collection of elements from a homogeneous material. We can thus conceptually replace the inhomogeneous composite by a continuous material described by material parameters ∊ and µ. At lower frequencies, conductors are excellent candidates from which to form artificial materials, because their response to electromagnetic fields is large.

A metamaterial mimicking the Drude–Lorentz model can be straightforwardly achieved with an array of wire elements into which cuts are periodically introduced. The effective permittivity for the cut-wire medium has the form $$\epsilon \left(\omega \right)=1-\frac{{\omega }_{\text{p}}^2-\omega \frac{2}{0}}{{\omega }^2-{\omega }_0^2+i\omega \Gamma },$$ (1) where the plasma frequency ω _p and the resonance frequency ω ₀ are determined only by the geometry of the lattice rather than by the charge, effective mass, and density of electrons, as is the case in naturally occurring materials. For ω ₀ < ω < ω _p, the permittivity is negative and, because the resonant frequency can be set to virtually any value in a metamaterial, phenomena—including negative ∊—usually found at optical frequencies can be reproduced at frequencies as low as a few megahertz. Structures are often designed with continuous wires so that ω ₀ = 0.

The path to achieving magnetic response from conductors is slightly different. From the basic definition of a magnetic dipole moment, m = $\frac{1}{2}$ ∞r X j d³ r for current density j, one can see that a magnetic response can be obtained if local currents can be induced to circulate in closed loops. Introducing a resonance into the element should enable a very strong magnetic response, potentially one that can lead to a negative µ.

In 1999, one of us (Pendry) and colleagues proposed a variety of structures that, they predicted, would form magnetic metamaterials. ² Those structures consisted of loops or tubes of conductor with a gap inserted. One can view such structures as miniature circuits: A time-varying magnetic field induces an electromotive force in the plane of the element, driving currents within the conductor. A gap in the plane of the structure introduces capacitance into the planar circuit and gives rise to a resonance at a frequency set by the geometry of the element. Such a splitring resonator (SRR), in its various forms, can be viewed as the metamaterial equivalent of a magnetic atom. The SRR medium could be described by the resonant form $$\mu \left(\omega \right)=1-\frac{F{\omega }^2}{{\omega }^2-{\omega }_0^2+i\omega \Gamma }.$$ (2)

The wire medium and the SRR medium represent two basic building blocks—one electric, the other magnetic—for a large range of metamaterial response, including Veselago’s hypothesized material (see figure 1).

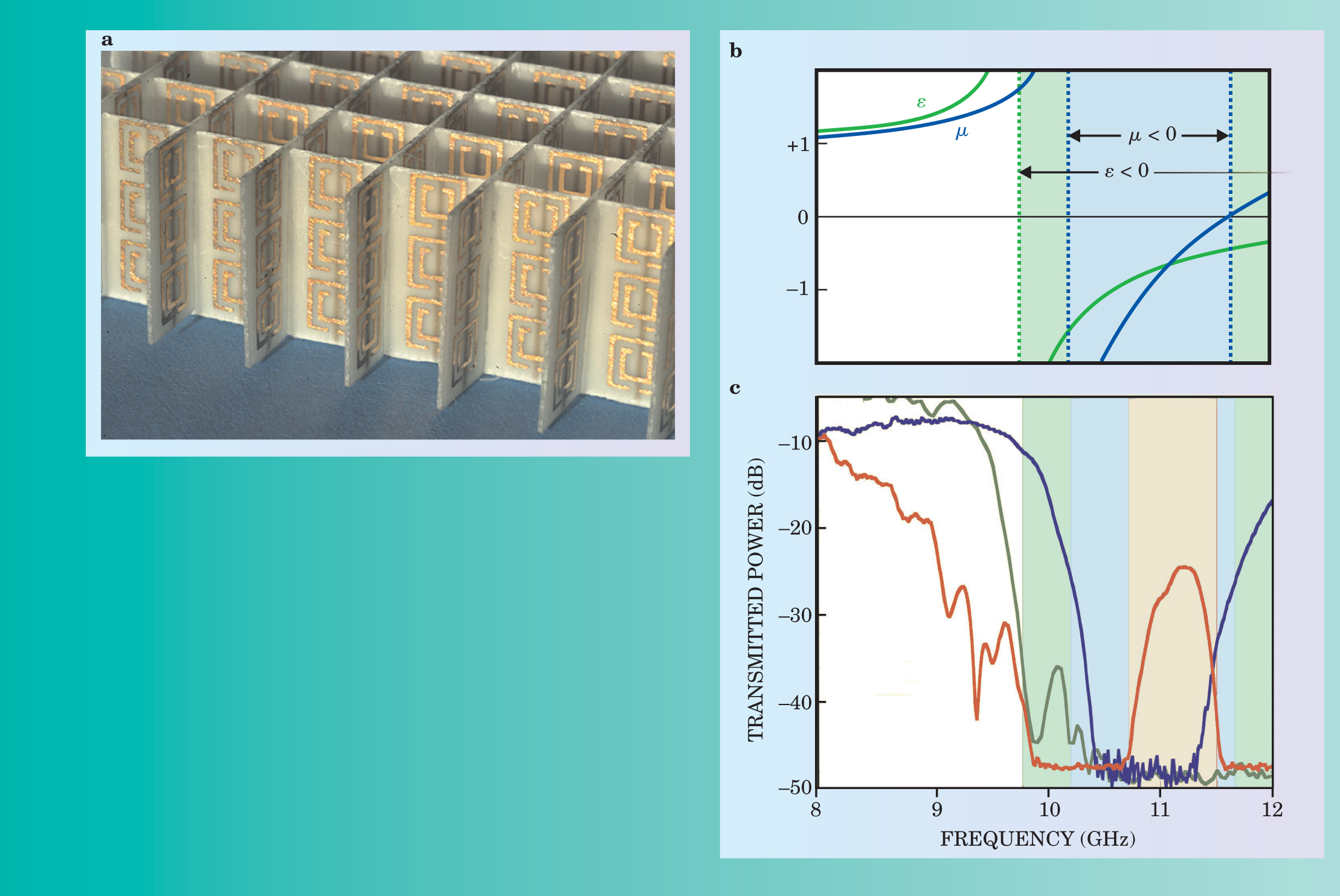
Negative refraction

Maxwell’s equations determine how electromagnetic waves propagate within a medium and can be solved to arrive at a wave equation of the form $$\frac{\partial E\left(x,t\right)}{\partial x^2}=\epsilon \mu \frac{{\partial }^{2}E\left(x,t\right)}{\partial t^2}.$$ (3)

In this equation, ∊ and µ enter as a product, so it would not appear to matter whether their signs were both positive or both negative. Indeed, solutions of the wave equation have the form exp[i(nkd − ω t)], where $n=\sqrt{∊\mu }$ is the refractive index. Propagating solutions exist in the material whether ∊ and µ are both positive or both negative. So what, if anything, is the difference between positive and negative materials?

It turns out that one needs to be more careful in taking the square root, because ∊ and µ are analytic functions whose values are generally complex. There is an ambiguity in the sign of the square root that is resolved by a proper analysis. For example, if instead of writing ∊ = −1 and µ = −1 we write ∊ = exp(iπ) and µ = exp(iπ), then $n=\sqrt{ϵ\mu }=\exp (i\pi /2)\exp (i\pi /2)=\exp \left(i\pi \right)=-1$ . The important step is that the square root of either ∊ or µ alone must have a positive imaginary part—a necessity for a passive material.

This briefly stated argument shows why the material Veselago pondered years ago is so unique: The index of refraction is negative. A negative refractive index implies that the phase of a wave decreases rather than advances with passage through the medium. As Veselago pointed out, this fundamental reversal of wave propagation contains important implications for nearly all electromagnetic phenomena. Many of the exotic effects of negative index have been or are currently being pursued by researchers. But perhaps the most immediately accessible phenomenon from an experimental or computational point of view is the reversal of wave refraction, illustrated in figure 2.

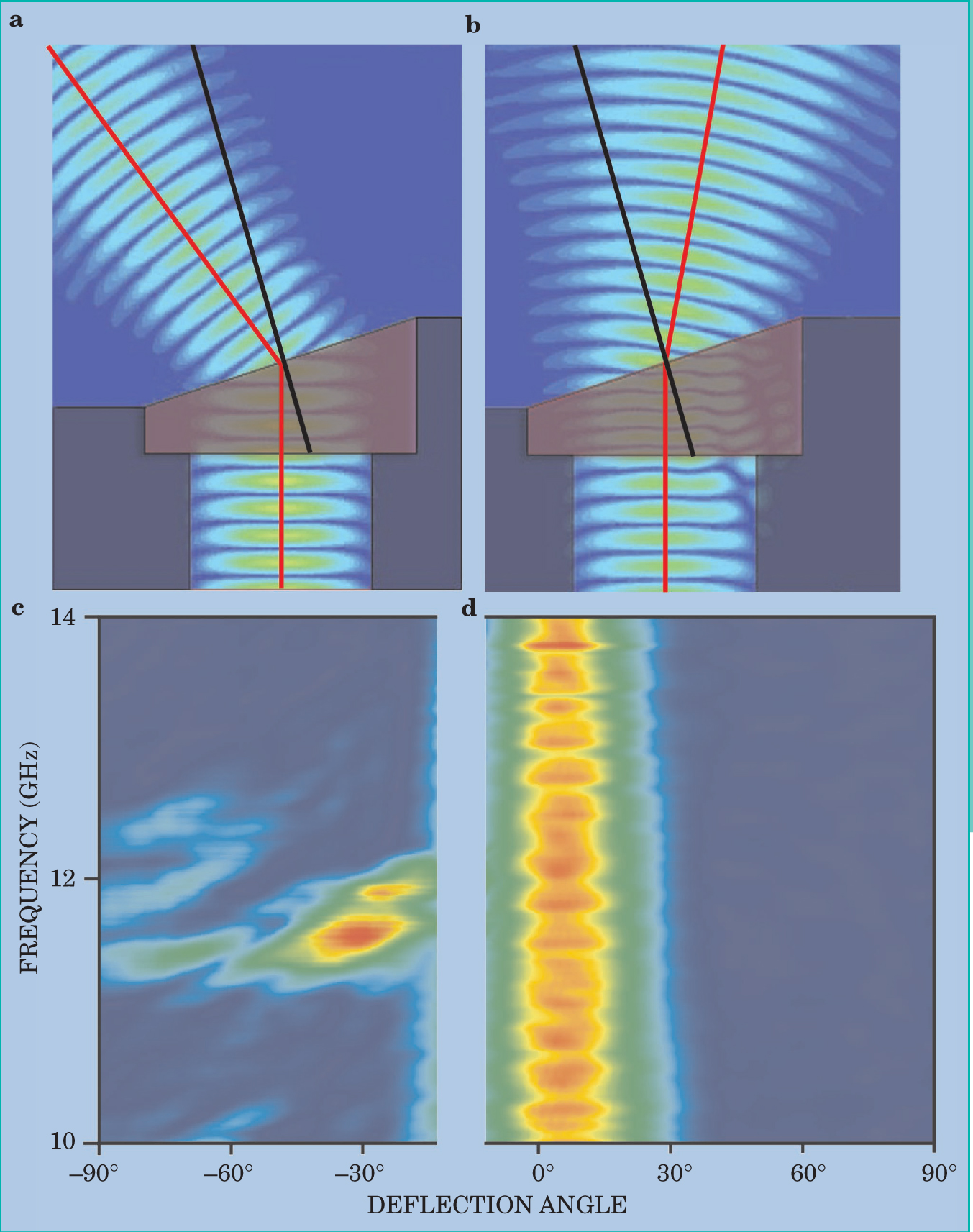
Snell’s law, which describes quantitatively the bending of a wave as it enters a medium, is perhaps one of the oldest and most well known of electromagnetic phenomena. In the form of a wedge refraction experiment, as depicted in figure 2, Snell’s law is also the basis for a direct measurement of a material’s refractive index. In this type of experiment, a wave is incident normal to a wedge-shaped sample. The wave is transmitted through the transparent sample and strikes the second interface at an angle. Because of the difference in refractive index between the material and free space, the beam exits the wedge deflected by some angle from the direction of incidence.

One might imagine that an experimental determination of Snell’s law would be a simple matter. The peculiarities of metamaterials, however, add a layer of complexity that renders the experimental confirmation somewhat more difficult. Present samples, based on SRRs and wires, are frequency dispersive with fairly narrow bandwidths and exhibit considerable loss. The first experiment showing negative refraction was performed in 2001 by one of us (Smith) and colleagues at the University of California, San Diego. ³ In an experiment similar to that depicted in figure 2, they measured the power refracted from a two-dimensional wedge-shaped metamaterial sample as a function of angle, confirming the expected properties.

While the UCSD data were compelling, the concept of negative index proved counterintuitive enough that many other researchers needed further convincing. In 2003, Andrew Houck and colleagues at MIT repeated the negative-refraction experiment on the same sort of negative-index metamaterial and confirmed the original findings. ⁴ Looking at wedges with different angles, the MIT group showed that the observed angle of refraction was consistent with Snell’s law for the metamaterial. In the same year, Claudio Parazzoli and coworkers at Boeing Phantom Works also confirmed the negative-refraction results in a separately designed sample. ⁵ In their measurements, the detector’s distance from the sample was significantly larger than for previous demonstrations.

Although it has proven to be a valuable concept, a rigorously defined negative index of refraction may not necessarily be a prerequisite for negative-refraction phenomena. An alternate approach to attaining negative refraction uses the properties of photonic crystals, ^6,7 materials that lie on the transition between a metamaterial and an ordinary structured dielectric. Photonic crystals derive their properties from Bragg reflection in a periodic structure engineered in the body of a dielectric, typically by drilling or etching holes. The periodicity in photonic crystals is on the order of the wavelength, so that the distinction between refraction and diffraction is blurred. Nevertheless, with photonic crystals many novel dispersion relationships can be realized, including ranges in which the frequency disperses negatively with wave vector as required for a negative refraction. Using photonic crystals, ^8,9 researchers have observed focusing, as predicted for negative-index materials.

The concept of negative refraction has also been generalized to transmission-line structures, which are common in electrical engineering applications. By pursuing the analogy between lumped circuit elements and material parameters, George Eleftheriades and coworkers at the University of Toronto have demonstrated negative-refraction phenomena in microwave circuits. ¹⁰ The transmission-line model has proven exceptionally valuable for the development of microwave devices: Tatsuo Itoh and Christophe Caloz at UCLA have applied the model to develop novel microwave components, including antennas, couplers, and resonators. ¹¹

Those experiments and applications have shown that the material Veselago hypothesized more than 35 years ago can now be realized using artificially constructed metamaterials; the discussion of negative refractive index is thus more than a theoretical curiosity. The question of whether such a material can exist has been answered, and the development of negative-index structures has turned into a topic of materials—or metamaterials—physics. As metamaterials are being designed and improved, we are now free to consider the ramifications associated with a negative index of refraction. That material property, perhaps because it is so simply stated, has enabled the rapid design of new electromagnetic structures—some with very unusual and exotic properties.

A better focus

Refraction is the phenomenon responsible for lenses and similar devices that focus or shape radiation. Although usually thought of in the context of visible light, lenses are utilized throughout the electromagnetic spectrum; they thus represent a good starting point to implement negative index materials.

In his early paper, Veselago noted that a negative-index focusing lens would need to be concave rather than convex—a seemingly trivial matter, but there is more to the story. For thin lenses, geometrical optics—valid for either positive or negative index—gives the result that the focal length f is related to the lens’s radius of curvature, R, by f = R /(n − 1). The denominator in the focal-length formula implies an inherent distinction between positive-and negative-index lenses: A material with n = +1 does not refract electromagnetic fields, whereas a material with n = −1 does. The result is that negative-index lenses can be more compact, with a host of other benefits, as shown in figure 3.

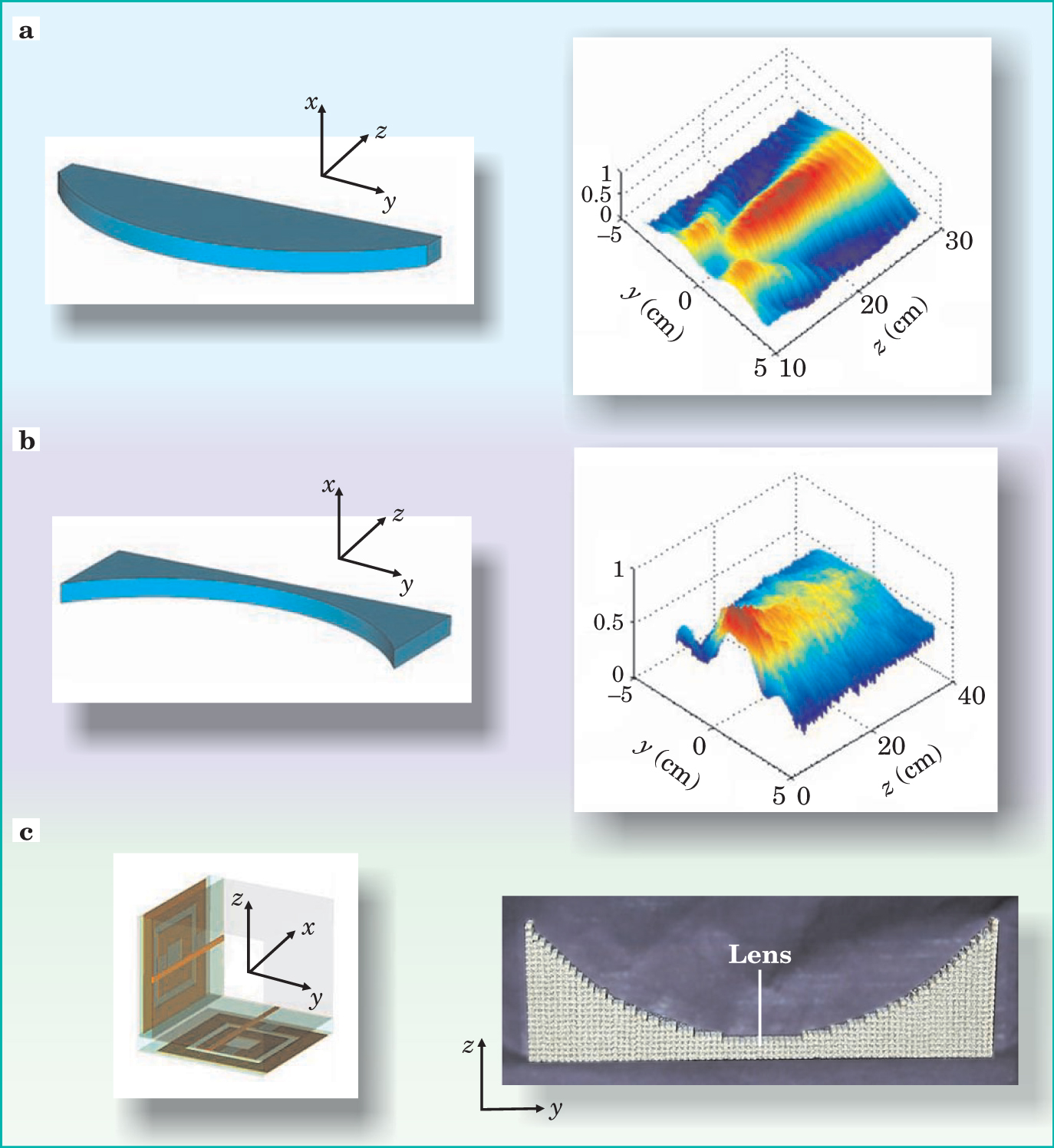
Making a conventional lens with the best possible resolution requires a wide aperture. Each ray emanating from an object, as shown in figure 4(a), has wave vector components along the axis of the lens, k _z = k ₀cosθ, and perpendicular to the axis, k _x = k ₀sinθ, where k ₀ is the wavenumber and θ is the angle of the ray with respect to the axis. The axial projection k _z is responsible for transporting the light from object to image; k _x represents a Fourier component of the image. For good resolution, the larger one can make k _x, the better. The best that can be achieved is k _x = k ₀, and hence the resolution limit is ▵ ≈ π/k ₀ = λ/2, where λ is the wavelength. This restriction is a huge problem in many areas of optics. The feature size achieved in computer chips and the storage capacity of DVDs, for example, are wavelength-limited. Even a modest relaxation of the wavelength limitation would be of great value.

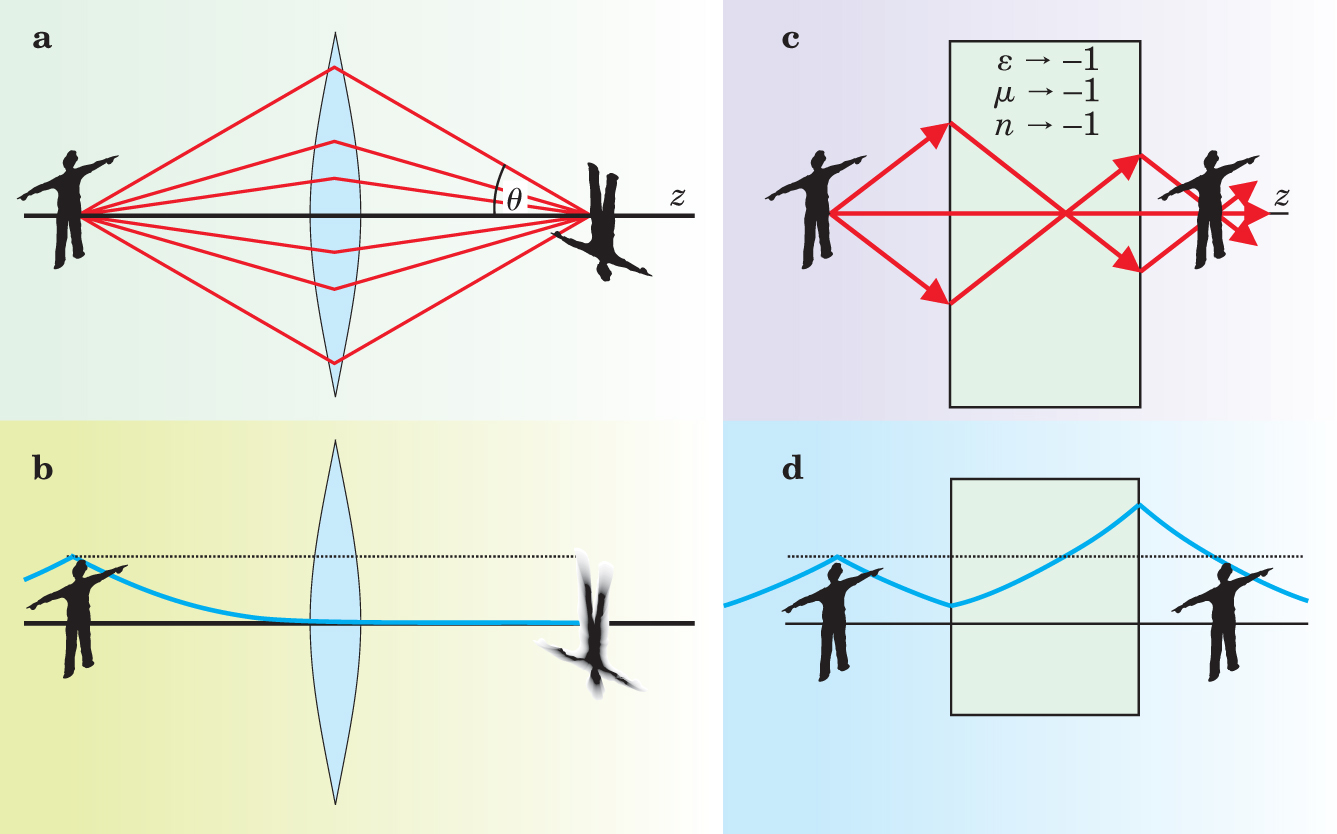
In contrast to the image, the object has no limit to its electromagnetic details, but unfortunately not all of that information makes it across the lens to the image. The problem lies with the wave vector’s z-component, which we can write as $k_z=\sqrt{k_0^2-k_x^2}$ . Evidently, for large values of k _x, corresponding to fine details in the object, k _z is imaginary and the waves decay exponentially as $\text{exp}\left(-\sqrt{k_x^2-k_0^{2}z}\right)$ , as shown in figure 4(b). By the time these so-called evanescent waves reach the image, they have negligible amplitude. For that reason, they are commonly referred to as the “near field” and the propagating rays as the “far field.”

If by some magic we could amplify the near fields, we could in principle recoup their contribution, but the amplification would have to be of just the right amount and possibly very strong for the most localized components. That is a tall order, but by a remarkable chance, a planar slab of negative material achieves this feat. ¹²

Figure 4(c) shows rays contributing to the image formed by a negative slab. Just as for a conventional lens, the rays only contribute details greater than about half a wavelength in diameter. In contrast, the behavior of the near field is remarkably different, as shown in figure 4(d). The near field has the capacity to excite short-wavelength resonances of the negative-index surface that are akin to the surface plasmons on the surfaces of metals such as silver. Interaction with the plasmonlike excitation kicks the decaying wave into a growing wave. The negative medium thus amplifies the wave and compensates for the decay that occurred in an equal thickness of vacuum. The resonances have a finite width and the requirement of ∊ = −1 and µ = −1 can be met only at one frequency because of the inherent dispersion of negative media. Therefore, this super lensing effect is a narrow-band phenomenon.

In the case of evanescent waves, amplification does not imply a sustained input of power. Evanescent waves carry no power and hence, in the absence of loss, a large-amplitude evanescent wave can be sustained indefinitely in a purely passive medium.

For a conventional lens, resolution is limited by the aperture. This new lens based on negative materials will also, in practice, have limitations, chiefly due to losses. Any real material will always have small, positive imaginary components to ∊ and µ that represent resistive losses in the system and damp the resonances responsible for amplifying the near fields. Because of their high quality factors Q, the sharpest resonances give the greatest amplification, but they are also the most susceptible to energy dissipation: They are the first to be killed by the losses, so with increasing loss the resolution is rapidly degraded.

Nick Fang and colleagues ¹³ have explored near-field amplification by exploiting the fact that for very small systems—much smaller than the free-space wavelength—the electric and magnetic fields are independent of one another and can be controlled separately. Therefore if one is only concerned with the electric fields, µ is irrelevant and one need only ensure that ∊ is negative.

Silver has a negative real part to ∊ and therefore a thin film should behave like a negative-index slab and amplify the near field. Fang and coworkers experimented on several silver films of different thickness, but each time selected the same k _x. The film clearly amplified waves up to a critical film thickness of about 50 nm, above which losses intervened and the amplification process collapsed. Nevertheless, considerable amplification is possible: Amplification factors of around 30 were achieved before collapse. Thus we can be optimistic that some limited subwavelength focusing can be achieved with silver films.

With a microwave transmission-line lens, Eleftheriades’s group in Toronto ¹⁰ has recently realized conditions for subwavelength focusing and produced images significantly enhanced by evanescent-wave amplification. The image resolution of about λ/5 was consistent with losses in the system; reducing the loss would improve resolution even further.

Negative refraction as negative space

A slab of negative material with ∊ = µ = −1 acts like a lens: Objects on one side are brought to a focus on the other side. As shown in figures 5(a) and 5(b), as a wave progresses through the negative medium, its phase is wound backward. Overall, the slab undoes the effect of an equal thickness of vacuum. Similarly, decaying waves have their amplitude restored by passing through the slab. These effects suggest another view of the focusing action, that of the slab annihilating an equal thickness of vacuum. One can see why materials with negative n are so special: Negative media behave like optical antimatter.

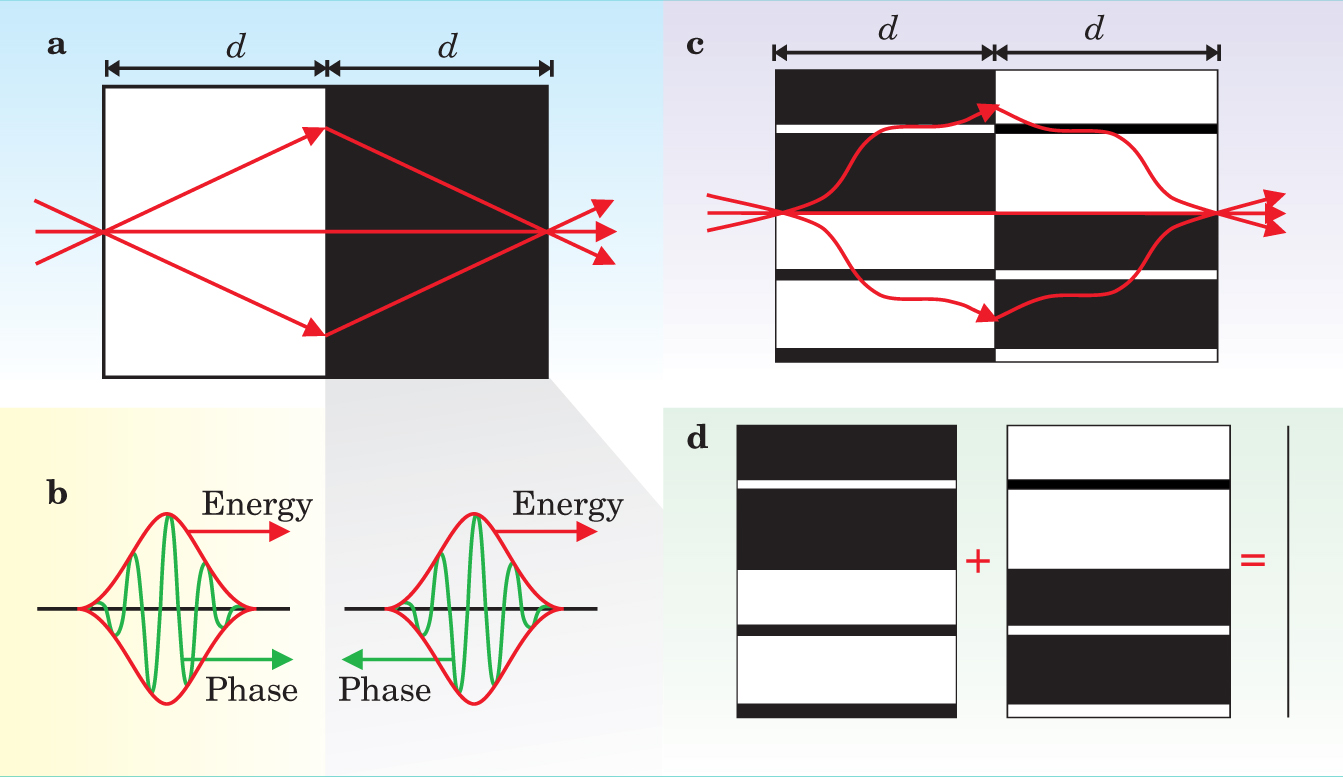
In fact, the result is more general. ¹⁴ Two slabs of material optically annihilate if one is the negative mirror image of the other—that is, if they meet in the plane z = 0 and, at equal and opposite distances from that plane, ∊(x, y, z) = −∊(x, y, −z) and µ(x, y, z) = −µ(x, y, −z).

Figures 5(c) and 5(d) illustrate the cancellation. The two media have varying refractive indices, and in general, light does not follow a straight line. Nevertheless, complementary paths in each medium are traced such that the overall phase acquired in the first medium is canceled by the contribution from the second. Likewise, if the waves have a decaying nature, decay in one half would be followed by amplification in the other.

This result may seem straightforward, but some configurations have surprises. The two halves of figure 6(a) are inverse mirror images as required by the cancellation theorem, and therefore we expect that incident waves are transmitted without attenuation and without reflection. Yet a ray-tracing exercise holds a surprise. Ray 2 in the figure hits the negative cylinder and is twice refracted to be ejected from the system rather than transmitted. The rays don’t support our theorem!

Further investigation shows that the cylinder is capable of trapping rays in closed orbits, shown by dotted lines in the center of the figure. Such closed paths are the signature of a resonance and a clue as to how the paradox is resolved. A full solution of Maxwell’s equations shows that when the incident light is first switched on, the ray predictions are initially obeyed. With time, some of the incident energy will feed into the resonant state in the middle of the system, which in turn will leak energy into a transmitted wave and into a contribution to the reflected wave that cancels with the original reflection. As always in negative media, resonant states play a central role.

Figures 6(b) and 6(c) show the equilibrium solutions. With only the negative sphere in figure 6(b), there is strong scattering. Figure 6(c) includes the mirror-antisymmetric layer that, within the accuracy of the calculations, removes the reflected contributions and the spurious forward scattering to leave transmission unhindered, as predicted.

An interesting question arises if there is absorption—represented by positive imaginary parts of either or both of ∊ and µ—in the system. Conditions for the theorem may still be satisfied but require that for every instance of a positive part to ∊ or µ, there is a mirror-antisymmetric negative part somewhere else in the system. In other words, parts of the system must exhibit gain: Loss can only be compensated by active amplification with a sustained input of power.

Building on the foundations

Negative refraction is a subject with constant capacity for surprise: Innocent assumptions lead to unexpected and sometimes profound consequences. This new field has generated great enthusiasm but also controversy, yet even the controversies have had the positive effect that key concepts have been critically scrutinized in the past 18 months. In the past year, experimental data have been produced that validate the concepts. As a result, we have a firm foundation on which to build. ¹⁵ Many groups are already moving forward with applications. The microwave area has naturally been most productive, because the metamaterials required are easier to fabricate. In addition to microwave lenses, novel waveguides and other devices are under consideration.

One of the most exciting possibilities is imaging beyond the wavelength limit. Practical applications will require low-loss materials, which are a great challenge to the designers of new metamaterials. Proposals to employ thin silver films as lenses are being explored in several laboratories. And the challenges are not purely experimental: We are not yet done with theory, because the assumption of negative refraction has many ramifications that are still being explored and are sure to cast more light on this strange but fascinating subject. Not surprisingly, many researchers are joining the field: 2003 saw more than 200 papers published on negative refraction. We expect even more in 2004!