Quantum turbulence
DOI: 10.1063/1.2731972
The turbulent flow of ordinary fluids is so common that we hardly stop to wonder at it. Yet it is a remarkable and beautiful phenomenon, portrayed in insightful drawings by Leonardo da Vinci such as those shown in figure 1. Turbulence is of enormous importance in fields ranging from meteorology to aerospace engineering and stellar evolution. Understanding turbulence presents us with some of the most challenging problems in classical nonlinear dynamics (see figure 2).

Figure 2. Turbulent flow of water (a) past a cylinder of diameter d at two increasing values of the Reynolds number Re, a dimensionless velocity parameter given here by ρvd/η, where v is the free-stream velocity and ρ and η are the water’s density and viscosity. The eddies downstream of the obstacle become smaller with increasing Re. (b) Turbulence initiated by flow through a grid.
(
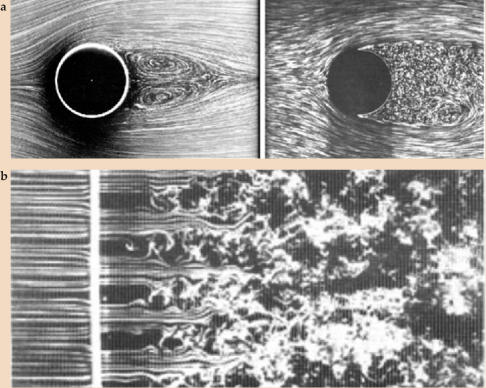

Figure 1. Leonardo da Vinci’s Studies of Water Passing Obstacles and Falling, circa 1508–09.

Although physicists, including some of the most distinguished, have occasionally been drawn into the study of turbulence, it is now for the most part the province of applied mathematicians and engineers. Perhaps that’s because physicists are more interested in quantum phenomena. Which raises the question of whether turbulent flow is always a purely classical phenomenon. Can it ever be influenced by quantum effects? Of course, the flow of a superfluid is a quantum phenomenon. So we are led to ask whether turbulence is possible in a superfluid. And if it is possible, how does the resulting interplay of quantum and classical fluid mechanics actually work out?
The idea that turbulence is possible in a superfluid was first mentioned in 1955 by Richard Feynman as a theoretical possibility. 1 At about the same time, Henry Hall and one of us (Vinen) were finding experimentally that certain types of superflow do indeed exhibit turbulent characteristics. 2 There was some study of these special types of superflow in the years that followed. But strangely, there was for many years hardly any study of what one might call the quantum analogues of well-known classical forms of turbulence. In the past 10 years, however, the situation has changed, and researchers are at last starting to ask how quantum effects can, in fact, influence classical turbulence.
Superfluidity and quantum turbulence
At first what is now called quantum turbulence was studied only in superfluid helium-4, which exists at temperatures below 2.2 K. The name was introduced by one of us (Donnelly) and defended in a 1986 review article. 3 More recently, study of quantum turbulence has been extended to the superfluid phases of the rare isotope 3He, especially to its low-temperature phase, 3He-B. That relatively simple phase 4 occurs at temperatures below 2 mK. In the near future, we can expect to see a further extension of quantum turbulence to Bose-condensed gases at microkelvin temperatures.
In the context of quantum turbulence, the important properties of all these superfluids can be summarized as follows. 5 They exhibit two-fluid behavior: a viscous normal fluid, formed from thermal excitations, coexisting with an inviscid superfluid. The fraction of normal fluid falls from unity to zero as the temperature falls from the superfluid transition to absolute zero. And the two components have separate velocity fields, v n and v s.
Superfluid behavior has its origin in the formation of a coherent particle field—the condensate wavefunction—associated with Bose condensation of 4He atoms or Bardeen-Cooper-Schrieffer condensation of Cooper pairs of 3He atoms. Flow of the superfluid component is associated with gradients in the phase of the condensate wavefunction. As a result, the superfluid flow is subject to severe quantum restrictions, essentially the quantization of angular momentum. Locally the flow must be irrotational; that is curl v s must vanish. And irrotational flow around an annulus is restricted in such a way that the circulation, defined as the line integral
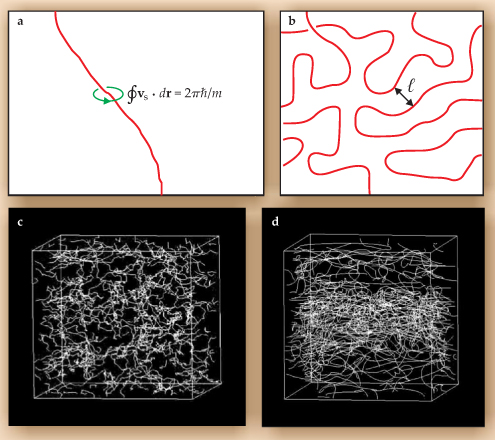
What is effectively an annulus can be created in the bulk of the fluid by suppressing superfluidity along a thin cylindrical volume, or core, extending along its length to the boundaries of the fluid. And a single quantum of circulation, κ = 2πħ/m, around this cylinder leads to the quantized vortex line shown in figure 3(a). The suppression of superfluidity in the core of the vortex is associated with destruction of the condensate at a high velocity. It is energetically favorable to lose superfluidity when the kinetic energy of the flowing superfluid becomes too large. The resulting core radius is roughly 0.1 nm for 4He, and 80 nm for 3He-B at low pressure. For the most part, quantized vortex lines appear to move in accordance with the laws of classical fluid mechanics.

Figure 3. (a) A single quantized vortex line is like a miniature tornado with a core diameter of order 1Å in superfluid helium-4. The line integral of superfluid velocity v s around any closed loop enclosing the core is the quantum of circulation, namely 2π h/m, where m is the relevant elementary mass of the superfluid’s constituents. The circulating velocity falls off as the reciprocal of the distance from the core. (b) A schematic vortex tangle illustrating the average spacing ℓ between vortex lines. (c) Computer simulation of an evolving tangle of vortex lines in helium-4 at zero temperature.
(Simulation figures courtesy of Makoto Tsubota.)
Two-fluid behavior leads to the phenomenon of second sound, which is a lightly damped temperature wave in which the two fluids move in opposite phase. Second sound has proved to be an important tool in the study of quantum turbulence. 2
Turbulence, by its nature, involves the random formation of eddies with rotational motion (see figure 2). Because such rotational motion in the superfluid component is made possible only by the presence of quantized vortex lines, superfluid turbulence is restricted to some more or less random tangle of vortex lines (see figures
Experimental challenges
The experimental study of quantum turbulence involves peculiar difficulties. Turbulence in a classical fluid such as water or air can be seen with the naked eye, especially if the flow is seeded with small tracer particles. But suitable particles with which to seed a superflow must be more or less neutrally buoyant. That’s difficult for a low-density fluid such as liquid helium. Furthermore, the particles must not aggregate, and they must be small enough to exhibit the micron scale on which quantum turbulence can occur.
More seriously, interpretation of the movement of tracer particles in a two-fluid system is not straightforward. Are they tracking the motion of the normal fluid or the superfluid, or are they trapped on the quantized vortex lines? There has recently been some experimental 6 and theoretical 7 progress in the application of tracer particles in superfluid 4He. But there’s a long way to go before the technique can provide unambiguous information. The velocity with which a tracer particle moves is complicated and hard to understand.
Alternatively, one can measure pressure gradients associated with turbulent flow in a tube and the forces on obstacles past which there is turbulent superflow. In the presence of vortex lines, there is a frictional interaction, called mutual friction, between the normal and superfluid components. That interaction arises from the scattering of thermal excitations by the vortex lines. Measurement of mutual friction through its damping effect on second sound has been used extensively to obtain information about the density of vortex lines in different flows. The technique is analogous to measuring the mean square vorticity in classical flows. Vorticity is defined as curl v.
Another potentially powerful technique is based on a measurement of pressure fluctuations within the superflow. Pressure fluctuations can be related to fluctuations in turbulent flow velocities. And with care, they can be used to obtain turbulent energy spectra E(k), where E(k)dk is the turbulent energy associated with wavenumbers in the range dk in a spatial Fourier analysis of the velocity field. These spectra reveal how the turbulent energy is distributed over different length scales—that is, over different eddy sizes.
Great interest attaches to quantum turbulence at very low temperatures (low compared with 1 K in 4He, and with 1 mK in 3He), where the density of normal fluid is very small. At such temperatures, experimenters face the most serious challenge. There, measurement of mutual friction in 4He becomes practically impossible. Even establishing interesting types of flow is difficult because very little dissipation of energy is enough to raise the temperature out of the interesting range. Indeed, the energy in the turbulent velocity field itself can be comparable with the fluid’s thermal energy. Therefore, an observation of the temperature rise can provide information about the decay of turbulence.
For 3He-B at very low temperatures, the scattering of a very small residual density of thermal quasiparticles by the superfluid velocity field has a special character. It’s called Andreev scattering. George Pickett and colleagues at the University of Lancaster in England have shown how such scattering yields interesting information about turbulent intensities and their spatial extent. 8 But there remain some problems of detailed interpretation.
Quantum versus classical turbulence
Despite the experimental difficulties that stand in the way of studying quantum turbulence, relatively simple experiments have clarified much about its general nature. Rather than review results from a wide range of experiments, we focus here on two aspects of quantum turbulence that are especially interesting: the similarities between quantum turbulence and its classical counterparts, and the origin of dissipation in quantum turbulence in the absence of viscosity in the superfluid component.
The first hint that classical and quantum turbulence may not be so different came from experiments by Jean Maurer and Patrick Tabeling 9 in Paris in the late 1990s. Studying turbulent flow generated by counterrotating disks, they obtained the turbulent-energy spectrum from measurements of the spectrum of pressure fluctuations in liquid 4He above 1 K. The finite spatial resolution of their pressure transducer meant that they could obtain the turbulent-energy spectrum only for wavelengths greater than about 1 mm. The spectrum observed by Maurer and Tabeling proved to be exactly the same at all temperatures from above the superfluid transition down to 1.4 K, where the fraction of normal fluid is only 4%.
Furthermore the spectrum had, to a good approximation, the classical Kolmogorov form,
where C is a constant of order unity and ε is an energy flux per unit mass. The meaning of ε and the physics underlying this spectrum can be summarized thus:
10
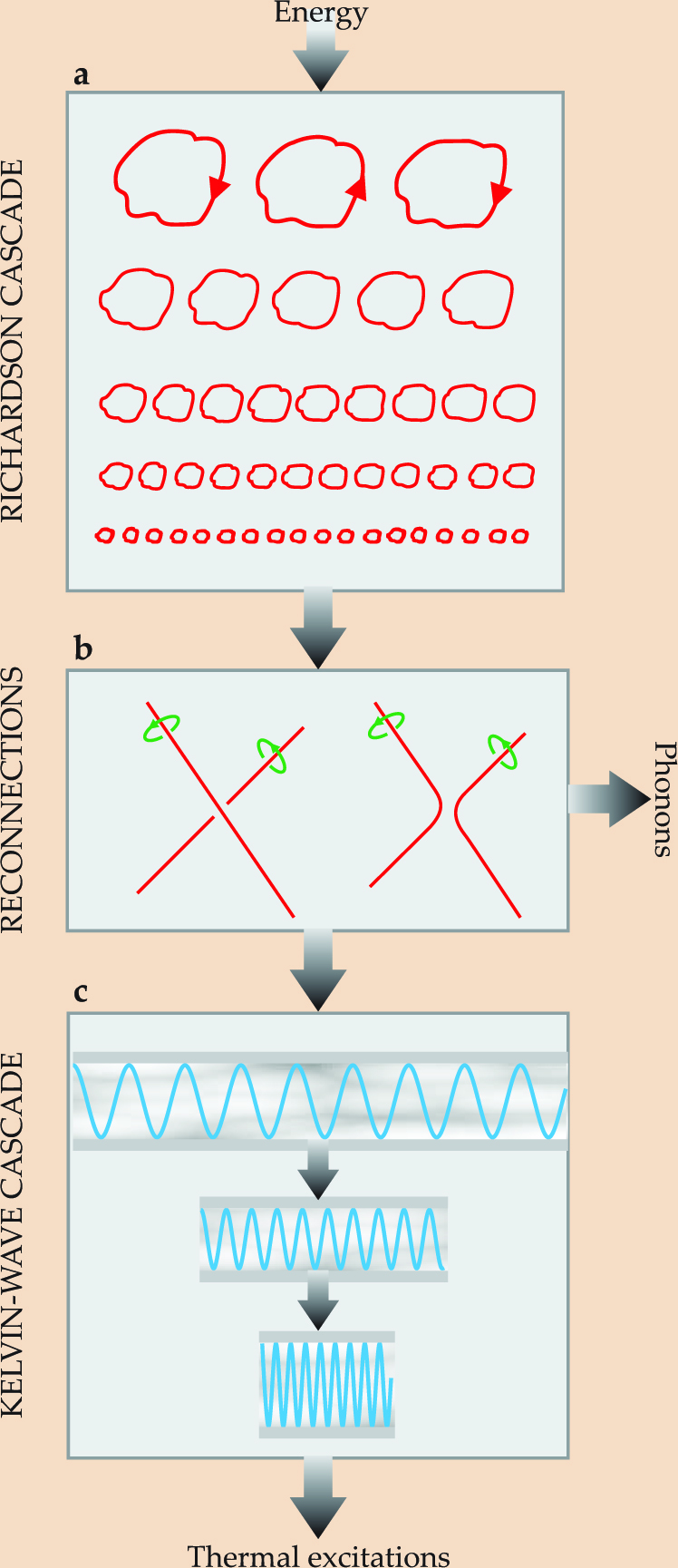
In a typical turbulent flow that’s at least approximately homogeneous, energy is injected at large length scales (small k). In the Maurer–Tabeling experiments, the rotating disks provide this injection on the scale of the disk diameter. If the Reynolds number Re for the flow on that large scale is much greater than unity, then a nonlinear coupling due to the (v · ∇)v term in the Navier–Stokes equation serves to transfer energy to smaller eddies without loss. That probably happens in a so-called Richardson cascade (see figure 4a), until the scale of the turbulent flow is so small (Re of order unity) that the energy is finally dissipated by viscosity. (See the article by Gregory Falkovich and Katepalli Sreenivasan in Physics Today, April 2006, page 43

Figure 4. How quantum turbulence might evolve in a superfluid at very low temperature.
The Kolmogorov spectrum describes the distribution of energy over k scales in the so-called inertial range where the dissipation is negligible, and the flux ε describes the steady-state flow of energy in k space. At the lowest k, the flux must equal the rate of energy injection, and at highest k, it must equal the rate of energy dissipation (by viscosity, in the case of a classical fluid).
At about the same time as the work of Maurer and Tabeling, experiments at the University of Oregon
11
were using second sound to measure the density of vortex lines in the wake of a steadily moving grid in superfluid 4He. Such a grid is commonly used to generate homogeneous turbulence in a classical fluid (see figure
The interpretation of the Oregon experiments is not straightforward, but a plausible interpretation of the results is as follows:
10,11
Denote the typical spacing between adjacent vortex lines in the turbulent superfluid by ℓ (see figure
where ν’ is an effective kinematic viscosity for the two-component fluid. The quantity κ 2/ℓ4, which is proportional to the square of the vortex-line density, is an effective mean-square vorticity in the inviscid superfluid component.
Thus equation
The recognition that superfluid He can exhibit turbulence in which it seems to behave like a single classical fluid has generated much debate. A widely held view is that, on scales significantly greater than ℓ, the superfluid component itself behaves like a classical inviscid fluid. 10 In other words, eddy motion on a scale that encompasses many vortex lines behaves in a quasiclassical way that mimics a classic inviscid fluid rather well.
There are many ways to see that this interpretation of the experiments is probably right. One simple argument is that a system containing many quanta tends quite generally to behave classically. The overall picture is then that, on a large enough length scale, both the normal fluid and the superfluid component behave classically and exhibit Kolmogorov spectra. The mutual friction associated with the vortex lines couples the two fluids together, so that there are not only Kolmogorov spectra in each fluid but indeed a single classical velocity field with a single Kolmogorov spectrum.
The idea that arrays of vortex lines can mimic classical rotational flow is visualized most easily for a superfluid in equilibrium in a rotating vessel. A uniform array of vortex lines leads to a superfluid velocity field indistinguishable from uniform rotation on any scale that’s large compared with the line spacing. More general types of rotational flow are generated by patterns of partially polarized vortex lines—that is, lines with some degree of alignment in both direction and sense of rotation.
On length scales not larger than ℓ, however, the motion of the superfluid is totally nonclassical. What, then, determines the value of ℓ? The Kolmogorov spectrum implies that the fluid velocity v(r), on length scale r, is given by
So velocity decreases with decreasing length scale at a rate determined by the rate of energy input at the largest scale. The vortex-line spacing ℓ is, in effect, the smallest possible eddy size consistent with the quantization of circulation. Thus v(ℓ) = κ/2πℓ. Therefore ℓ is determined by the equation
and is typically 10 microns when the large-scale flow velocity is of order 10 cm/s. This assumes that the Kolmogorov spectrum extends down to scales of order ℓ.
Much recent understanding of classical turbulence comes from computer simulations. The equations that govern the motion of quantized vortices are known. They are essentially classical, except for one feature that turns out to be very important—namely the possibility that two vortex lines can “reconnect” during a close encounter, as shown in figure
The picture we have been presenting in connection with the Maurer–Tabeling and Oregon experiments depends on the normal fluid having little viscosity, so that turbulence is possible in both fluids. That is, in fact, the case in 4He above 1 K; the viscosity of the normal fluid is so low that it has no viscous dissipation on scales larger than ℓ. But 3He-B is very different. The normal fluid has such a high viscosity that it cannot support turbulence on any laboratory scale. In principle, turbulence is still possible in the superfluid component, but it is inevitably damped by mutual friction between the two fluids.
This damping has been the subject of extensive studies by Matti Krusius and coworkers in Helsinki. 4 They have shown that, at temperatures not far below the superfluid transition, the damping is so strong that it effectively inhibits any turbulence in the superfluid component. At lower temperatures, the mutual friction is smaller, and turbulence can occur in the superfluid component, albeit with significant extra damping. Detailed theoretical studies 13 have explored the conditions under which homogeneous turbulence could be created in the superfluid component. But such turbulence has not yet been studied experimentally. The theory predicts that large eddies should be more strongly damped by mutual friction than small ones. That’s an interesting contrast to viscosity, which preferentially damps small eddies.
Dissipation in quantum turbulence
The Richardson cascade and the Kolmogorov energy spectrum depend on the existence of a dissipative process acting at small length scales. In classical turbulence, viscosity provides that dissipation. In superfluid 4He at temperatures above 1 K, where the fraction of normal component is significant, the dissipation is provided by a combination of normal-fluid viscosity and mutual friction. On large length scales, mutual friction has no effect because the velocity fields of the two components are identical, with no relative motion. But that happens only if the superfluid flow can be quasiclassical. And on scales comparable with the vortex spacing, such quasiclassical flow becomes impossible. Because the two velocity fields must differ at such small scales, mutual friction can operate.
Our discussion poses two important questions: Is quantum turbulence in the superfluid component quasiclassical even at temperatures so low that the normal fluid component is completely absent? And if so, what would then provide the necessary dissipation in the absence of mutual friction? Experiments that satisfactorily address these questions are proving difficult. All the experiments thus far involve the generation of turbulence by some sort of oscillating structure rather than by a steadily moving grid. Such experiments raise interesting questions, but they cannot generate turbulence that is even approximately homogeneous. Therefore, they can’t adequately verify the occurrence of a Richardson cascade and its associated Kolmogorov spectrum.
A mechanism for pulling a grid steadily through helium at the lowest temperatures is still under development, as are various turbulence probes for use in 4He at very low temperatures. For 3He-B, the Andreev scattering technique is yielding information about turbulence produced by an oscillating grid, and there is indeed some evidence of a Kolmogorov spectrum. But the inevitably inhomogeneous nature of turbulence produced by an oscillating structure stands in the way of really convincing evidence.
A number of experiments at very low temperatures in both 4He and 3He confirm that some dissipative process leads to the decay of turbulence even in the absence of normal fluid. They suggest that the process is associated with an effective kinematic viscosity comparable to κ, the quantum of circulation.
Looking at the experimental results on homogeneous turbulence in 4He at temperatures so low the fraction of normal fluid is less than 2%, we are tempted to assert that so little normal fluid could hardly force the superfluid to behave differently from its natural behavior in the complete absence of normal fluid. But convincing experimental evidence is still lacking.
Theoretical discussion of low-temperature quantum turbulence and the associated dissipation is, in fact, well ahead of the experiments. Quasiclassical behavior at absolute zero on length scales larger than the vortex spacing has been confirmed in simulations. 12 In the absence of viscosity and mutual friction, a turbulent fluid can lose energy only by acoustic radiation of sound or, in quantum language, emission of phonons.
For effective sound radiation, however, the turbulence must generate oscillating densities at sufficiently high frequencies. The frequencies associated with a tangle of vortex lines with separation ℓ are of order κ/ℓ2. For values of ℓ typical of quantum turbulence produced by a moving grid in 4He above 1 K, the frequencies are much too small. But nonlinear interactions cause turbulent energy to flow toward smaller and smaller length scales. The operation of a Richardson cascade depends on just such a flow.
The Osaka group’s computer simulations
12
show exactly what happens (see figures
Vortex reconnection is itself dissipative, and it produces some emission of excitations. The resulting dissipation is probably small, at least in the case of 4He, because of the small widths of the vortex cores. The origin of further dissipation is controversial. One picture is that repeated reconnections produce smaller and smaller vortex rings, whose collisions with each other produce high-frequency vortex motion.
Another picture
15
is that the repeated reconnections act like the plucking of a string, thus generating waves on the vortices called Kelvin waves (see figure
Thus the overall picture of turbulence in a superfluid at very low temperature might be the sequence shown in figure
It is possible to estimate the overall dissipation resulting from the processes shown in figure
Although quantum turbulence in the experiments discussed here was generated by the movement of a grid or some other structure through the superfluid, we have made no mention of the detailed processes occurring very close to the structures, analogous to the classical flows just downstream of the obstacles in figure 2. Experiments that probe such processes, especially in connection with oscillating structures at very low temperatures, are currently being carried out by the groups in Osaka, Lancaster, Regensburg, and Prague. Evidence is emerging, especially from measurements of drag, that the processes in 4He might indeed be similar to those occurring in classical flow. But the behavior of 3He-B seems to be different. 16
Behavior unique to quantum turbulence
We have focused here on aspects of quantum turbulence that have classical analogues. But some processes, for example the damping of quantum turbulence by mutual friction in 3He-B, have no classical analogue. A more striking example is provided by the first type of quantum turbulence to be discovered and studied experimentally by one of us (Vinen) in the 1950s. That type of turbulence is associated with the flow of heat in superfluid 4He at temperatures above 1 K. The heat flow is due to a counterflow of the two fluids. This counterflow can lead to the generation of quantum turbulence, even in the absence of any solid boundaries. The action of mutual friction in the counterflow leads to a self-sustaining tangle of vortex lines, in a way that was first clearly explained in pioneering computational work by Klaus Schwarz at IBM. 17 The effect depends on the forced movement of vortex lines by mutual friction. And the fact that it can be self-sustaining depends crucially on the presence of vortex reconnections. The effect has no classical analogue, and it serves to demonstrate that quantum turbulence can sometimes be richer than its classical counterpart.
The future
Turbulence continues to challenge our understanding, its quantum version no less than its classical version. In fact, the study of quantum turbulence is still in its infancy. Subtle questions that are now the subjects of extensive research in classical turbulence, such as intermittency and coherent structures, are only starting to be considered in the context of quantum turbulence. Experimenters need to develop more powerful experimental tools that can match those available to the student of classical turbulence.
The wider significance of quantum turbulence raises interesting questions. Are aspects of quantum turbulence applicable to other areas of physics? Grigory Volovik at the Helsinki University of Technology and the Landau Institute in Moscow suggests, for example, that quantum turbulence might have been important in the evolution of cosmic strings in the early universe. 18 It may also be that the study of quantum turbulence will throw light on problems still unsolved in classical turbulence. As yet, there are no clear answers.
We are grateful for discussions with many of our colleagues throughout the world who have made contributions to our understanding of quantum turbulence.
References
1. R. P. Feynman, in Progress in Low Temperature Physics, vol. 1, C. J. Gorter, ed., North-Holland, Amsterdam (1955). https://doi.org/10.1016/S0079-6417(08)60077-3
2. H. E. Hall, W. F. Vinen, Proc. R. Soc. London, ser. A 238, 204 (1956); https://doi.org/PRLAAZ
W. F. Vinen, in Progress in Low Temperature Physics, vol. 3, C. J. Gorter, ed., North-Holland, Amsterdam (1961). https://doi.org/10.1016/S0079-6417(08)60132-83. R. J. Donnelly, C. E. Swanson, J. Fluid Mech. 173, 387 (1986).https://doi.org/JFLSA7
4. A. P. Finne et al., Rep. Prog. Phys. 69, 3157 (2006).https://doi.org/RPPHAG
5. R. J. Donnelly, Quantized Vortices in Helium II, Cambridge U. Press, New York (1991);
D. R. Tilley, J. Tilley, Superfluidity and Superconductivity, 3rd ed., IOP, Philadelphia (1990).6. T. Zhang, D. Celik, S. W. Van Sciver, J. Low Temp. Phys. 134, 985 (2004);https://doi.org/JLTPAC
G. P. Bewley, D. P. Lathrop, K. R. Sreenivasan, Nature 441, 588 (2006).https://doi.org/NATUAS7. D. R. Poole, C. F. Barenghi, Y. A. Sergeev, W. F. Vinen, Phys. Rev. B 71, 064514 (2005).https://doi.org/PRBMDO
8. D. I. Bradley et al., Phys. Rev. Lett. 96, 035301 (2006);https://doi.org/PRLTAO
S. Fisher, G. Pickett, Phys. World 19(4), 22 (2006).https://doi.org/PHWOEW9. J. Maurer, P. Tabeling, Europhys. Lett. 43, 29 (1998).https://doi.org/EULEEJ
10. W. F. Vinen, J. J. Niemela, J. Low Temp. Phys. 128, 167 (2002).https://doi.org/JLTPAC
11. S. R. Stalp, L. Skrbek, R. J. Donnelly, Phys. Rev. Lett. 82, 4831 (1999).https://doi.org/PRLTAO
12. M. Tsubota, T. Araki, S. K. Nemirovskii, Phys. Rev. B 62, 11751 (2000); https://doi.org/PRBMDO
M. Kobayashi, M. Tsubota, Phys. Rev. Lett. 94, 065302 (2005).https://doi.org/PRLTAO13. W. F. Vinen, Phys. Rev. B 71, 024513 (2005); https://doi.org/PRBMDO
V. S. L’vov, V. Nazarenko, G. E. Volovik, JETP Lett. 80, 479 (2004).https://doi.org/JTPLA214. B. V. Svistunov, Phys. Rev. B 52, 3647 (1995).https://doi.org/PRBMDO
15. W. F. Vinen, J. Low Temp. Phys. 145, 7 (2006).https://doi.org/JLTPAC
16. R. Hänninen, M. Tsubota, W. F. Vinen, Phys. Rev. B 75, 064502 (2007).https://doi.org/PRBMDO
17. K. W. Schwarz, Phys. Rev. B 38, 2398 (1988).https://doi.org/PRBMDO
18. G. Volovik, The Universe in a Helium Droplet, Oxford U. Press, New York (2003).
More about the Authors
Joe Vinen is a professor of physics at the University of Birmingham in England. Russell Donnelly is a professor of physics at the University of Oregon in Eugene. They met shortly after completing doctoral work in low-temperature physics in 1956, and they’ve been discussing quantum turbulence ever since.
William F. Vinen. 1 University of Birmingham, England .
Russell J. Donnelly. 2 University of Oregon, Eugene, US .




