Quantum optomechanics

Give me a place to stand and with a lever I will move the whole world. —Archimedes

Over two millennia ago, scholars from antiquity had already come to understand the power of simple mechanical elements. And from that understanding they formulated an enduring, common-sense notion of the nature of reality, described thusly in Plato’s The Republic:

The same thing cannot ever act or be acted upon in two opposite ways, or be two opposite things, at the same time, in respect of the same part of itself, and in relation to the same object.

Today researchers at the cutting edge of physics are still exploiting simple mechanical elements as tools with which to carefully probe our world. But unlike their predecessors, they are preparing those elements deeply in the quantum regime and, in the process, challenging ancient notions of reality. Ironically, today’s devices, though similar in many ways to those of antiquity, steer us to a completely different worldview—one in which an object, possibly even a macroscopic one, can indeed act in two ways at the same time.

Two key developments, born of two converging perspectives on the physical world, have enabled the advance. From the top-down perspective, nanoscience and the semiconductor industries have developed advanced materials and processing techniques, which in turn have given rise to ultrasensitive micromechanical and nanomechanical devices. Such devices can probe extremely tiny forces, often with spatial resolution at atomic scales, as exemplified by the recent measurements of the Casimir force (see the article by Steve Lamoreaux, PHYSICS TODAY, February 2007, page 40 ) and the mechanical detection and imaging of a single electron spin (see PHYSICS TODAY, October 2004, page 22 ). From the bottom-up perspective, quantum optics and atomic physics have yielded an exquisite understanding of the mechanical aspects of light–matter interaction, including how quantum mechanics limits the ultimate sensitivity of measurements and how back-action—the influence a quantum measurement necessarily exerts on the object being measured—can be harnessed to control quantum states of mechanical systems.

Quantum optomechanics combines the two perspectives: By pairing optical or microwave cavities with mechanical resonators to form a cavity optomechanical system, one acquires a means to achieve quantum control over mechanical motion or, conversely, mechanical control over optical or microwave fields. The laws of quantum physics can then be made to reveal themselves in the motion of objects ranging in size from nanometers to centimeters, from femtograms to kilograms. Cavity optomechanical systems hold promise as a means to both observe and control the quantum states of macroscopic objects and to measure feeble forces and fields with a sensitivity, precision, and accuracy approaching the quantum limit ¹ (see the article by Keith Schwab and Michael Roukes, PHYSICS TODAY, July 2005, page 36 ).

Early optomechanics

Put simply, a cavity optomechanical system is an optical or microwave cavity that contains a mechanical element, a moving part that can support collective oscillation modes whose quanta of excitation are known as phonons. The system could be as simple as an optical cavity in which one of the end mirrors oscillates as if attached to a spring.

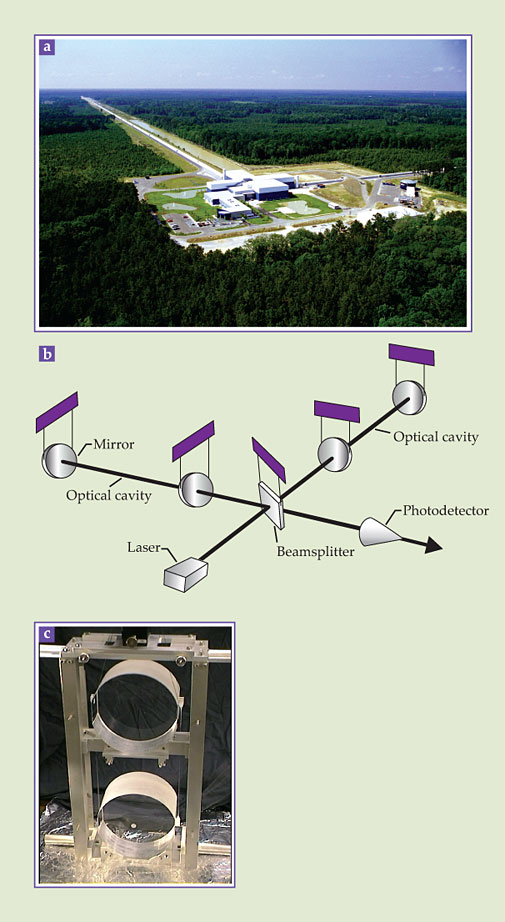
Among the first well-understood cavity optomechanical systems were the early gravitational-wave detectors developed in the late 1970s and early 1980s, with major contributions by Vladimir Braginsky, Kip Thorne, Carlton Caves, William Unruh, and others. ² Such detectors are essentially giant interferometers, with each arm being a kilometers-long optical cavity bounded by mirrors several kilograms in mass (see figure 1). In theory, a ripple in the local curvature of spacetime due to a passing gravitational wave should alter each cavity’s optical path length, modulate its resonance frequency, and, in turn, alter the optical transmission to a photodetector. The Laser Interferometer Gravitational-Wave Observatory, currently the gold standard of gravitational-wave detectors, can achieve displacement sensitivities as high as 10⁻¹⁹ m Hz^−1/2. In other words, it can detect a displacement of about 1/1000 of a proton radius based on a one-second measurement.

A related approach to detecting gravitational waves calls for using a massive, multiton cylinder as a gravitational-wave antenna. In theory, the cylinder should undergo bending oscillations in the presence of a passing gravitational wave. Provided the cylinder is integrated into a high-quality superconducting microwave cavity, that bending should detectably modulate the cavity’s resonance frequency. Although the interferometer and bar-antenna approaches to gravitational-wave detection deploy very different technologies, both rely on the underlying concept that mechanical motion can be harnessed to modulate an electromagnetic resonance.

Thirty years after the first deep studies of the limits of gravitational wave detectors, it’s evident to us that Braginsky, Caves, and their contemporaries had two very exciting things to say: First, gravitational-wave astronomy might be possible, and second, so might the measurement and manipulation of macroscopic objects at their quantum limits. ³ The second message has motivated an increasing number of mostly young researchers trained in areas as diverse as solid-state physics, quantum information, and computation to look for and exploit the quantum behavior of large mechanical objects in tabletop experiments.

Getting to zero

Quantum effects in any system are most pronounced when the influence of thermal fluctuations can be ignored. So, ideally, a mechanical quantum experiment would start with the mechanical element in its quantum ground state of motion, in which all thermal quanta have been removed. In practice, however, one settles for cooling the element such that for a given mechanical mode the time-averaged number of thermal phonons, the so-called occupation number N, is less than one. Put another way, the mean thermal energy k_BT should be less than the quantum of mechanical energy ℏω_m, so that N ≈ k_BT/ℏω_m < 1. Here k_B is Boltzmann’s constant, ℏ is the reduced Planck’s constant, T is the temperature, and ω_m is the frequency of the vibrational mode of the mechanical element.

Removing thermal phonons from the mechanical element is a key experimental challenge. Interestingly, the ideas and methods for doing so were theoretically developed as early as the 1960s. The main idea is to exploit the intracavity radiation pressure, the force due to momentum transfer associated with photon scattering. In particular, Braginsky realized that the finite time delay between a change in position of the mechanical element and the response of the intracavity field allows the radiation field to extract work from or perform work on the mechanical system.

The process is best illustrated for the case of a basic Fabry–Perot resonator (see figure 2). When both of the resonator’s mirrors are held fixed, the optical transmission is sharply peaked near the cavity resonance frequencies ω_p = pπc/L, where L is the mirror separation, p is a positive integer, and c is the speed of light. The resonances result from the constructive interferences between the partial waves propagating back and forth inside the cavity. The higher the quality of the mirror, the more roundtrips light takes before exiting the cavity, and the sharper are the resonance peaks.

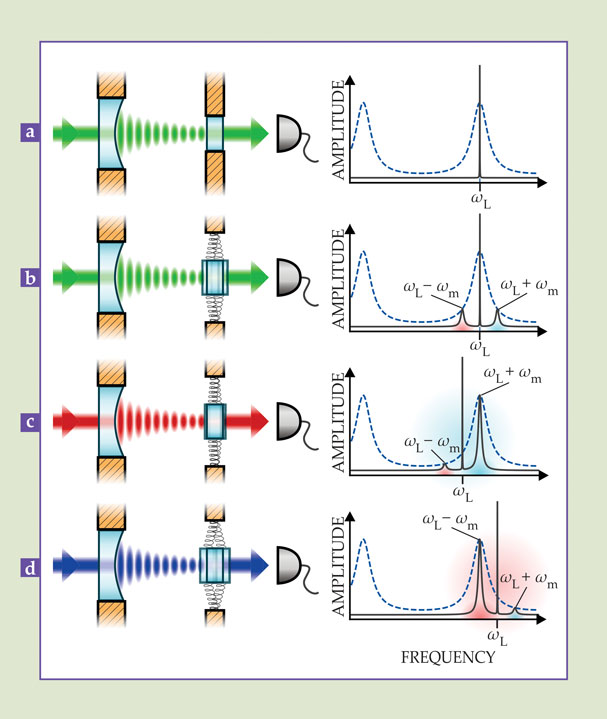
If one end mirror is mounted on a spring to form a simple harmonic oscillator, a pump laser of frequency ω_L will be modulated by the mechanical frequency and form sidebands with frequencies ω_L ± ω_m. From a quantum mechanical perspective, the process is analogous to the generation of Stokes and anti-Stokes sidebands in Raman scattering: The upper sideband is a result of pump-laser photons acquiring energy by annihilating thermal phonons in the mechanical element; the lower sideband results from photons depositing phonons and shedding energy. The first process occurs at a rate proportional to the occupation factor N of the mechanical mode of interest; the second, at a rate proportional to N + 1.

By carefully detuning the frequency of the pump field relative to a specific cavity resonance ω_c, one can resonantly enhance one of the processes. In particular, red-detuning from the cavity resonance enhances the upper sideband and promotes extraction of energy from the mechanical element. As long as the up-converted photons leave the cavity sufficiently fast, carrying with them their newly acquired energy, the process can cool the motion of the mechanical element to well below the temperature of its surroundings. Although the quantum noise of the optical source imposes a fundamental cooling limit, it is nonetheless theoretically possible to cool the mechanical mode arbitrarily close to the quantum ground state, N = 0. Furthermore, the coherent interaction between photons and phonons allows manipulations in the quantum regime, as pointed out early on by one of us (Meystre), Peter Knight, Paolo Tombesi, and Claude Fabre.

The technique, a form of sideband cooling, was first demonstrated in experiments by Braginsky and by David Blair in the microwave regime as a way to reduce noise in gravitational-wave antennas. ⁴ Since 2004, several laboratories around the world have used the method to cool nano- and micromechanical levers, in both the optical and microwave domains. Today, high-quality optomechanical devices produce couplings strong enough to cool low-mass levers—ranging from a few picograms to hundreds of nanograms—to their ground state of motion.

The methods used in cavity optomechanics are in many ways analogous to the conventional laser-cooling techniques developed for quantum information processing with trapped ions (see the article by Ignacio Cirac and Peter Zoller, PHYSICS TODAY, March 2004, page 38 ). There, the collective normal-mode oscillations of a string of ions modify the response of the pump laser that drives their internal state. The resulting optomechanical coupling between the ions’ motional and internal degrees of freedom allows one to cool the ions or prepare other quantum states of interest. ⁵ However, cavity optomechanics differs in an important and attractive aspect: Whereas conventional laser cooling relies on the fixed internal resonances of materials to enhance light–matter interactions, cavity optomechanical cooling allows one to engineer the resonance-enhancing structure. That structure could be an optical cavity with a series of narrow resonances or a microwave cavity such as a superconducting LC circuit.

A tale of few phonons

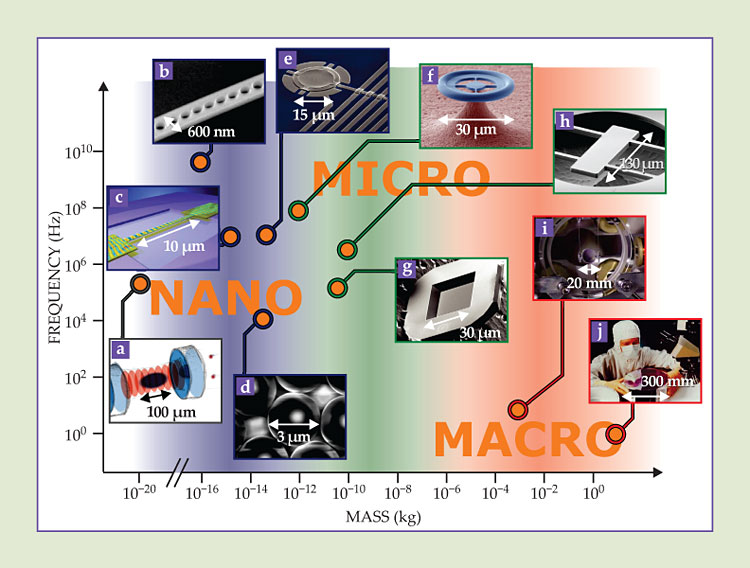
Until recently, the pioneering developments in optomechanical coupling went largely unnoticed outside of the experimental gravitation and quantum optics communities. Michael Roukes, who realized nearly two decades ago that high-frequency nanoscale mechanical devices could be chilled to the quantum regime, is a notable exception. Advances in materials science and nanofabrication—particularly the rise of nano- and microelectromechanical systems and optical microcavities—have since opened the possibility of coupling quantum optical modes with mechanical devices in tabletop experiments. ⁶ The original ideas of optomechanical coupling were extended in many new directions and realized in widely varied optomechanical systems (see figure 3). In the past year, those efforts have culminated in the cooling of at least three different micromechanical systems to within a fraction of a phonon of their ground state of vibrational motion. (Here and below, unless otherwise specified, mechanical cooling refers to cooling of the center-of-mass motion.)

In a NIST experiment led by John Teufel and Ray Simmonds, ⁷ the mechanical resonator was a circular aluminum membrane, 15 µm across and 100 nm thick, that underwent drum-like vibrations with a resonance frequency of 10 MHz (see figure 3e). The membrane was tightly coupled to a superconducting microwave cavity and chilled in a cryostat to 20 mK, at which the phonon occupation N was about 40. Sideband cooling was then used to cool the membrane to N ≈ 0.3.

At Caltech, Oskar Painter and colleagues were similarly successful using a 15-µm-long, 600-nm-wide, and 100-nm-thick silicon beam as the optomechanical system (see figure 3b). ⁸ Clamped at both ends to a silicon wafer, the suspended beam acts simultaneously as a mechanical resonator and an optical cavity. The mechanical mode of interest was a breathing mode, a periodic widening and narrowing that is most pronounced near the beam’s midpoint and has a remarkably high quality factor of 10⁵. (On average, a phonon survives 10⁵ oscillations before being lost to the environment.) And periodic perforations patterned into the beam create a photonic crystal cavity that confines light to the same region around the beam’s midpoint.

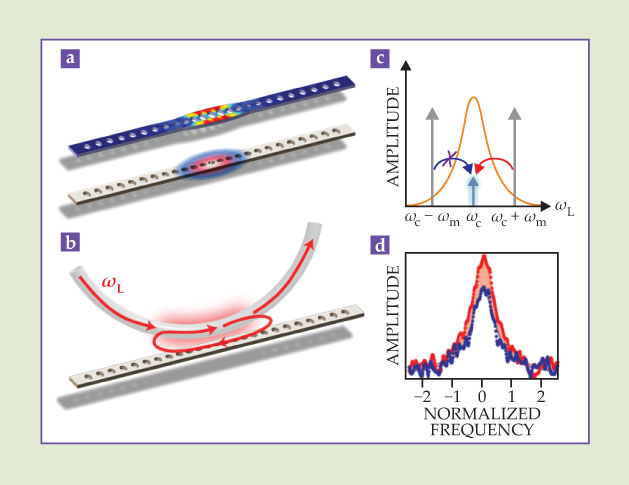
The co-localization of light and vibrational motion in such a small volume facilitates large optomechanical coupling. Thus, after cryogenically chilling the structure to 20 K, at which N ≈ 100, the researchers could use sideband cooling to remove the remaining phonons and cool the beam to N ≈ 0.8. At that point, the group was able to observe another genuine quantum feature: Near the ground state, a mechanical resonator is significantly more likely to absorb phonons than to emit them, and that asymmetry reveals itself experimentally as a preferential sideband scattering of blue-detuned light over red-detuned light. (See figure 4.)

The next challenge is to control the quantum state of the mechanical resonator. A group led by Andrew Cleland at the University of California, Santa Barbara, took an important first step in that direction by coupling an acoustic resonator to a qubit, a two-state quantum system. ⁹ The resonator was a 300-nm-thick sheet of aluminum nitride, 40 µm long and 20 µm wide, whose thickness oscillates at a frequency of 6 GHz. At such high oscillation frequencies, the phonon energy ℏω_m is large, and therefore a conventional dilution refrigerator—which can reach temperatures near 25 mK—sufficed to cool the resonator to an occupation factor N < 0.07.

Exploiting the piezoelectric nature of AlN, the Santa Barbara team then coupled the resonator to the qubit, a superconducting Josephson junction, which could in turn detect the presence of a single phonon. A null result meant the mechanical resonator was in the ground state. The technique is analogous to those that have been developed over the years in cavity and circuit quantum electrodynamics, except that the photons are replaced by phonons.

Not only did the resonator–qubit coupling allow observation of the energy quantization and other quantum features of the resonator, it also enabled controlled manipulation of the mechanical resonator at the few-phonon level. The Santa Barbara group was able to observe a few coherent oscillations of a single quantum exchanged between the qubit and the resonator—a first demonstration of coherent control over single quantum excitations in a micromechanical resonator. Recent experiments at Caltech and Harvard University and in Grenoble, France, have made important further steps by coupling mechanical devices to a variety of other qubits.

Single-quantum or few-quanta control can occur only in a strong-coupling regime, where energy is exchanged between the mechanical resonator and the qubit or optical mode with very little dissipation; loss of photons and phonons to the environment must be minimal. That regime has now been reached with several micromechanical devices in addition to the one used in the Santa Barbara experiment. ¹⁰ Eventually, such strong optomechanical coupling will allow high-fidelity transfer of quantum states between light and mechanical systems. It should even be possible to generate entanglement between photons and phonons. Conversely, phonon fields can be mapped onto an optical mode to take advantage of the reliable, high-efficiency detection schemes available in optics.

Promise in the field

The lure of quantum optomechanics goes far beyond simply adding another class of objects—mechanical resonators—to the list of “tamed” quantum systems. Rather, the promise is that just as we’ve learned to couple mechanical elements with the photons in an optical cavity, we can functionalize those same elements to couple with, say, the spins in a magnetic material or the charges at a conducting surface. That way, a mechanical element would serve as a universal transducer, an intermediary between otherwise incompatible systems. Flying photons could be linked with stationary, nonoptical qubits, for instance. Only recently, a group led by Philipp Treutlein at the University of Basel, Switzerland, has demonstrated a hybrid optomechanical system coupling ultracold atoms to a micromechanical membrane. Such hybrid quantum systems may be important in classical and quantum information processing, for which the ability to convert information from one form to another is crucial. In fact, several laboratories are now working to couple single mechanical elements to both optical and microwave frequency resonators, with the goal of connecting superconducting microwave circuits and qubits to optical fields.

The connection between optomechanics and atomic physics is particularly interesting. Not only did laser cooling of atoms inspire and enable the rapid progress in quantum optomechanics, it also led to the discovery of other phenomena such as optomechanically induced transparency, the analogue to electromagnetically induced transparency. The effect, which exploits optical interference between a mechanical resonator’s excitation paths to control the cavity transmission, may allow storage of light in arrays of cavity optomechanical devices. ¹¹

Atomic systems can also serve as mechanical elements in cavity optomechanical systems. ¹² After trapping 10⁵ ultracold rubidium atoms inside an optical cavity, Dan Stamper-Kurn and colleagues at the University of California, Berkeley, coupled the cloud of atoms with a pump laser that was detuned by the resonance frequency of the atoms’ collective motion, about 40 kHz. By blue-detuning the pump laser so that it deposited phonons into the cloud, the group was able to observe the back-action exerted on the atoms by the quantum fluctuations of the optical field.

The generation and manipulation of mechanical quantum states is also a challenging and important goal for quantum metrology and sensing applications. To date, the force sensitivity of atomic force microscopes and other classical mechanical devices already exceeds 10⁻¹⁸ N Hz^−1/2. In other words, in less than a second, one can measure a force as small as the gravitational attraction between a person in Los Angeles and another in New York. Still, we haven’t reached the ultimate limit. Current implementations suffer from thermal noise and, eventually, from noise associated with quantum uncertainty.

Fortunately, quantum physics provides a way around thermal and quantum noise by way of what are known as quantum nondemolition measurements. Such measurements, first posited in the 1970s by Braginsky and coworkers, typically call for generating a squeezed state—that is, confining the unwanted but unavoidable quantum noise to a variable that is complementary to the variable of interest.

Heisenberg’s uncertainty principle states that certain pairs of physical properties—say, the amplitude and phase of an electromagnetic wave—cannot simultaneously be known with arbitrary precision. But a measurement of the wave’s amplitude can be performed in such a way that most of the uncertainty is carried by the phase, or vice versa. Such squeezed states of light have recently been shown to enhance the sensitivity of gravitational-wave detectors ¹³ (see PHYSICS TODAY, November 2011, page 11 ).

In principle, it is also possible to prepare mechanical squeezed states in which nearly all of the quantum uncertainty is confined to either the position or the momentum. In fact, the classical squeezing of micromechanical oscillators below the thermal noise limit was first demonstrated several years ago by Daniel Rugar and colleagues at IBM. ¹⁴ However, squeezing below the standard quantum limit—the precision limit for the case when quantum uncertainty is distributed evenly among complementary properties—has yet to be achieved. A number of strategies based on Braginsky’s original schemes, which can be readily implemented in optomechanical systems, are being actively pursued.

Macroscale quantum mechanics

Although still speculative, micromechanical oscillators could offer a route to new tests of quantum theory at unprecedented size and mass scales. Since fundamental particles behave quantum mechanically, one would by induction expect that large collections of particles should also behave quantum mechanically. But that conclusion certainly seems contrary to our everyday classical experience with ordinary matter. Even large quantum condensates—a cupful of superfluid helium, for instance—which do display quantum properties such as frictionless, quantized flow, do not display macroscopic superposition states.

To explain the so-called quantum measurement problem, also notoriously known as Schrödinger’s cat, some theorists propose that standard quantum mechanics breaks down for macroscopic objects in such a way that their superposition is forbidden. In one such theory, gravitation, which is always unshieldable, ultimately causes massive objects to decohere, or transition from quantum to classical behavior. In another theory, objects couple to a stochastic background field that localizes the object at a rate that scales with the number of particles.

Quantum optomechanics offers a promising way to produce spatial superpositions in massive objects such as mechanical levers or quartz nanospheres and to directly test theories of how they decohere. ¹⁵ Ongoing work in that direction builds on optical-trapping and optical-cooling techniques originally proposed by Arthur Ashkin ¹⁶ and should eventually allow a single trapped particle to be prepared in a quantum superposition of two distinct center-of-mass states.

Approaching the problem from the opposite direction—from the bottom up—researchers in Vienna used conventional molecular-beam techniques to produce matter-wave interferences with large, 430-atom molecules. ¹⁷ Ultimately, it may be possible to conduct similar quantum experiments with even more massive mechanical systems. A group led by Nergis Mavalvala of MIT recently took a first step in that direction by cooling a kilogram-size oscillator to within about 200 phonons of the quantum ground state. ¹⁸

Macroscale mechanical quantum experiments will have to overcome a number of daunting technical issues. Some of those issues—identifying gravity’s role in decoherence, for example—might be resolved by conducting experiments in free fall, perhaps aboard a satellite. (Last year’s Caltech experiment, in which a phonon occupancy of less than one was achieved at a bath temperature of 20 K, shows that ground-state cooling is now within the range of commercial cryocoolers that can be flown on satellites.) We are confident that coming experiments will lead to a more profound understanding of quantum mechanics, establish limits to its validity, or confirm what we, and likely many others, believe—that technical issues such as environmental decoherence, and not the appearance of new physical principles, establish the transition from the quantum world to the classical. We have never been so close to being able to truly address those profound questions and to challenge Plato’s commonsense notion of reality in the laboratory.