Quantum numbers, Chern classes, and a bodhisattva

For two and a half years, starting in January 1946, I was a graduate student in the physics department of the University of Chicago. During that period Enrico Fermi often joined several of us for lunch in a campus cafeteria called the Commons. Among those participating were Marvin Goldberger, Geoffrey Chew, Owen Chamberlain, and Joan Hinton. Later Marshall Rosenbluth, T. D. Lee, and others also joined. Once in 1948 Fermi brought a short and lean Frenchman to the cafeteria. That day it was mostly the two of them who talked. Afterwards we asked Fermi who that person was, and he said it was André Weil, an important mathematician. He also said Weil was speculating that the new particles and quantum numbers physicists were finding might be related to a classification scheme that mathematicians were developing in geometry and topology. None of us at the time understood what Weil had meant.

In retrospect, I think Weil was visiting the university that day to discuss with mathematics department chairman Marshall Stone the possibility of joining the department. The visit was apparently successful: Weil—and later, mathematician Shiing-Shen Chern—accepted Stone’s offer, thus ensuring the brilliance of Chicago’s mathematics department during the 1950s.

Around 1960 Chern went west to the University of California, Berkeley, and Weil went east to the Institute for Advanced Study in Princeton, New Jersey. Chern told me Weil had joked that Chern went west to be closer to China and Weil went east to be closer to France. For the next five or six years Weil and I were colleagues at the institute. But we were not in the same field, and we had little occasion to talk about math or physics. Thus I never did ask him to explain what he had said at that lunch in Chicago in the late 1940s.

Physics meets geometry

In the 1970s I learned from James Simons about the close relationship between gauge theory and the mathematicians’ fiber-bundle theory. He also told me about the Chern class, the deep Chern–Weil theorem, and Weil’s influential review of Chern’s seminal paper of 1944, a paper that had opened the door to the science of global differential geometry. (For context and some details, see the box.) I then realized that during his 1948 lunch visit to Chicago, Weil was likely speculating on the possibly deep connection between some of the physicists’ quantum numbers and the characteristic classes of global differential geometry.

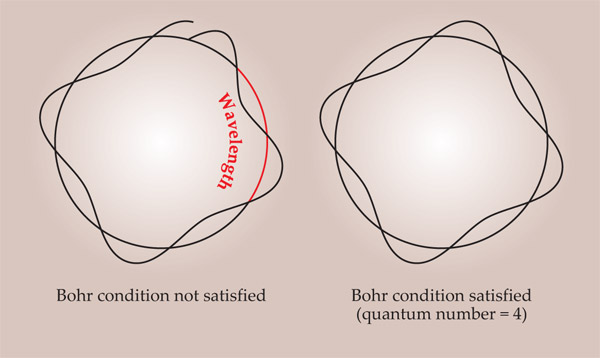
Was that speculation of Weil’s reasonable? I now think yes, very reasonable. The fundamental structure of the universe is geometric, a point repeatedly emphasized by Albert Einstein and firmly held by most theoretical physicists today. Furthermore, the Chern class and similar concepts from global differential geometry are clearly similar in spirit to the concept of quantum numbers in Bohr’s theory involving circular orbits, as illustrated in the figure. After all, the circle is a global object.

Chern reflected on his accomplishments in a little story he told in 1987. The story has been widely retold, often in embellished and unreliable versions. An accurate version appears in Chern’s papers, selections of which have been published in Chinese. There Chern wrote,

One year my wife and I visited a luohan (arhat) pagoda. I said to her, “No matter how good one’s math is, one is still a luohan at most.” A bodhisattva’s name is known to all, but a luohan’s name is known to none. So one should not be overly concerned about names. Why was [Bernhard] Riemann’s work important? Because like other scientific disciplines, mathematics must constantly enlarge its domain. What everyone pays attention to are works that creatively extend.

I deconstruct that passage as follows: Chern at that time believed he had attained the class of luohan, but not yet that of bodhisattva. Is that self-evaluation overly modest? I am not a mathematician and should be careful about making any comments. But if Weil’s 1948 speculation turns out to be correct, then Chern’s creative extension of differential geometry will relate to a most fundamental structure of the physical universe. Would the future main hall of the temple of mathematics not welcome its new bodhisattva?

From polyhedra to wrapped surfaces

The characteristic class introduced by Shiing-Shen Chern in 1946 is associated with an integer—roughly speaking, the number of times a closed surface is wrapped around another closed surface. For the elementary case in which the closed surfaces are one-dimensional, simple, closed loops, the Chern-class number is exactly the Bohr quantum number introduced in 1913 and illustrated in the figure at the bottom of the page.

The conceptual origins of the Chern class may be found in the polyhedron theorem of Leonhard Euler. Consider the representative polyhedra in the table to the right and note that the final column—vertices minus edges plus faces—is always 2. The polyhedron theorem asserts that the same number, 2, results for all regular or irregular convex polyhedra.

When the number of corners becomes infinite, the surface becomes smooth and Euler’s theorem becomes the Gauss–Bonnet theorem, which was formulated and proven in the 19th century. In 1943 Carl Allendoerfer and André Weil generalized the Gauss–Bonnet theorem to higher dimensions, through their careful considerations of “Riemannian polyhedra,” “dual and outer angles,” and complicated triangulation. The proof was very difficult to understand. Furthermore, it required embedding the surface in a higher-dimensional Euclidean space, and thus it was not intrinsic. A few weeks after reading Allendoerfer and Weil’s paper, Chern used the exterior differential forms invented by Élie Cartan and the theory of vector bundles to produce an intrinsic proof that was only six pages long. That proof opened the door to a vibrant and rich branch of mathematics called global differential geometry and led naturally to such concepts as the Chern class.