Quantum materials out of equilibrium
DOI: 10.1063/PT.3.5001
To appreciate some of the most interesting quantum phenomena associated with electrons in a material, imagine a flock of birds. Although each individual bird has its own flight pattern, the flock as a whole moves in sync and avoids any collisions. Such collective motion is ubiquitous in nature and is behind a central concept in condensed-matter physics: emergence. It describes how assemblies of objects behave in ways fundamentally different from their individual constituents. Examples include social networks and superconducting materials, whose collective properties come from pairs of electrons. As Nobel laureate Philip Anderson explains in his 1972 article “More is different,” understanding that collective behavior is a fundamentally different task than understanding isolated components. 1

JOERG M. HARMS AND ANDREA CAVALLERI/MAX PLANCK INSTITUTE FOR THE STRUCTURE AND DYNAMICS OF MATTER

Most theories developed to understand collective behaviors in materials hold only in the presence of equilibrium conditions, such as when energy is conserved. But releasing a physical system from that equilibrium constraint—for example, by introducing a time-dependent external force—can lead in quantum materials to exotic states of matter that have no equilibrium analogue. Such states are highly sought in the field of quantum many-particle systems. A good illustration is a time crystal, an externally driven time-dependent system in which particles in the lowest energy state are in constant, repetitive motion (see the article by Norman Yao and Chetan Nayak, Physics Today, September 2018, page 40
In this article we discuss the properties of quantum materials in out-of-equilibrium conditions induced by laser irradiation. Remarkably, light pulses from a laser can also control the ordered states of a material. That control has led to important insights in such strongly correlated materials as high-temperature superconductors. 2 Laser parameters, such as intensity, polarization, and frequency, are important variables for tuning material properties out of equilibrium. Lasers and other selectively chosen drives open the possibility of creating—at ultrafast speeds—systems with tailor-made physical properties at the touch of a switch.
To follow the important ideas in the field of out-of-equilibrium quantum materials, we first develop some intuition for the concept of a quantum material. What kinds of ordered states can arise from interactions among electrons, and what kinds of topological properties can emerge? We then discuss how laser irradiation can modify those properties.
Topology, energy bands, and collective modes
Think of a quantum material as a collection of atoms that have interacting electrons and nuclei and that exhibit emergent behavior and topological properties—that is, properties that are impervious to local defects. Figure
Figure 1.

A real-space illustration of a quantum material (a) displays interacting degrees of freedom: electron spins (blue arrows), electron orbitals (green lobes), phonons (black springs), and an incoming laser beam (yellow). The magnetic exchange parameter
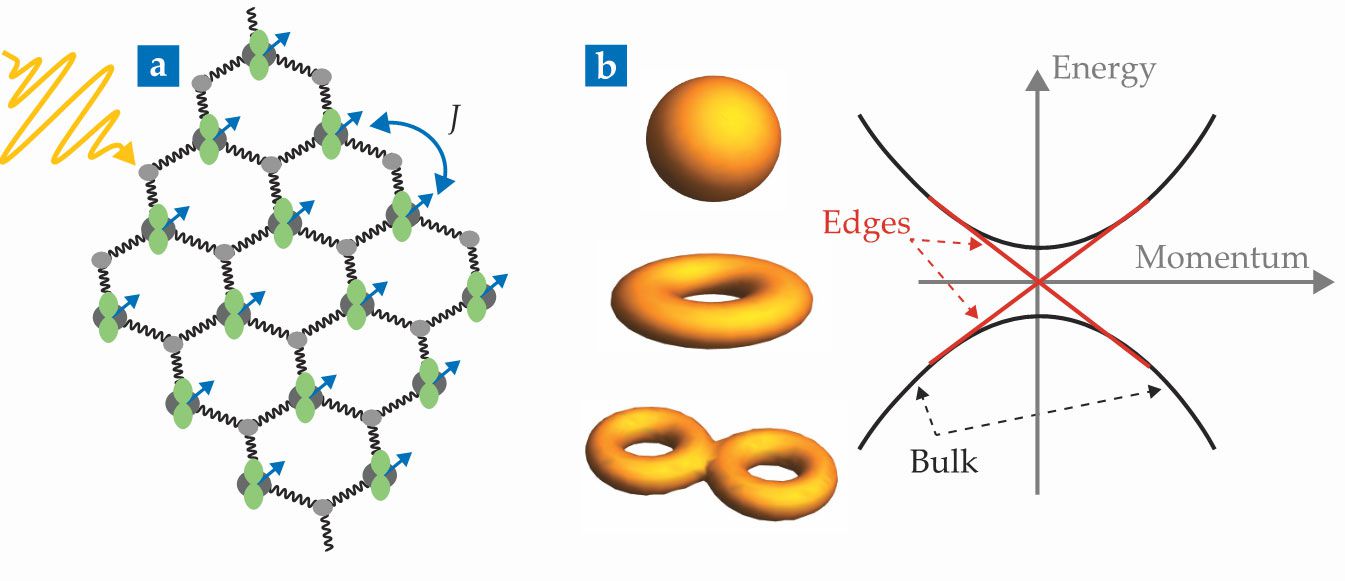
Ever since the discovery in 1980 of the integer quantum Hall effect in two-dimensional systems, topological phases have played an important role in the field. With their extension to 3D systems in the late 2000s, topological phases have come to dominate the landscape of solid-state physics. Topology is an intrinsic property of electronic band structure, which describes the energy–momentum relations of electrons in a crystal lattice. Different topological materials exhibit previously unknown phases of matter. For example, many topological materials are insulating in the bulk but conduct an electric current on the surface or edges.
The modern theory of topological band structure—topological quantum chemistry—is built on symmetry-based considerations and complements chemical theories of bonding, ionization, and covalence. Consequently, it describes the global properties of all possible band structures. And its application to solids has resulted in fast searches for existing compounds and rapid predictions of new materials. Detailed studies have shown that topological materials are far more common than previously thought. 3
Despite its dramatic successes, topological quantum chemistry does not extend to materials whose collective modes—lattice vibrations called phonons and magnetic fluctuations called magnons—and their interactions are fundamental to understanding the material behavior. Instead, one must consider such strongly correlated materials on a case-by-case basis. For example, the Coulomb interactions between electrons can produce insulating materials that even electronic band theory would predict to be metallic.
4
Such interaction-induced insulators are called Mott insulators. They are often described in terms of local moment (spin) models with collective spin excitations and a Hamiltonian,
In the context of nonequilibrium quantum materials, collective modes play an outsized role because they are often the most interesting to selectively excite with a laser. Each collective mode—induced by correlations that result from interactions—possesses different excitation energy scales. Across materials, however, one can discern a range of distinct energies. For example, in insulating materials, the excitation energy of electrons can be measured in electron volts. On the other hand, lattice and spin collective modes are typically less energetic: Phonon energies are in the few tens to low hundreds of millielectron volts, and magnons are in the few millielectron volts or even lower. That energy hierarchy, combined with constraints imposed by the symmetries of the material, opens the door to selective mode excitation in quantum materials. See the box on page
Phonons in group theory
Symmetry is one of the most fundamental concepts in physics. It is also quite useful. The symmetry of a crystal lattice in its equilibrium state determines the symmetries of the lattice’s vibrational modes, even when the crystal is out of equilibrium. Selectively exciting specific modes with a laser can tailor the topology of a material’s electronic band structure and manipulate its magnetic states. The figure illustrates the equilibrium lattice symmetries of chromium triiodide (CrI3), a two-dimensional magnetic insulator at low temperatures. Blue dots represent chromium atoms, and purple dots iodine atoms. The CrI3 lattice has twofold rotational symmetry about the center of a chromium hexagonal lattice unit because of the lower symmetry arrangement of the iodine atoms.
The application of symmetry to physics has far-reaching implications and is much broader than lattice vibrations. In her 1918 work “Invariant variation problems,” Emmy Noether showed that symmetries are mathematically associated with conserved physical quantities. The conservation of energy, for example, is associated with the time-translational symmetry of physical laws derived from time-independent Hamiltonians.
Each quantum material is characterized by its own set of crystal symmetries, which are the mathematical operations that when performed on a material structure leave it unaltered. Translations and rotations are examples. (See the 2008 book Group Theory: Application to the Physics of Condensed Matter, by Mildred Dresselhaus, Gene Dresselhaus, and Ado Jorio, for a pedagogical introduction.)

The collection of crystal symmetries defines the space group of the material, which includes the translational symmetries. Each material is constructed by repeating its unit cell. Typically, the space group of a material is established through a combination of group-theory studies and x-ray or neutron scattering experiments.
Once the material symmetries are established, one can determine the phonons’ symmetries. In the case of phonons excited by light, the discussion can be restricted to long-wavelength phonons. Mathematically, one need consider only point groups. For example, the point group of monolayer CrI3 is D3d, one of the 32 point groups in three spatial dimensions.
Group theory can also help block-diagonalize the dynamical matrix, which determines the real-space atom motions for each phonon type. That is done by constructing the projection operators for each phonon type. Those displacements do not correspond directly to the actual phonons but form a basis for them. To determine the energetics of the phonons, one must employ density functional theory.
Among all the possible collective modes, phonons draw special attention because their excitation by laser radiation can modify a crystal’s lattice structure and profoundly affect its electronic phase. Technological advances in intense ultrashort terahertz light pulses allow researchers to selectively excite phonons coherently (see the article by Joe Orenstein, Physics Today, September 2012, page 44
Achievements with laser driving
An important caveat is that direct laser excitation works only for certain types of phonons as determined by the symmetries of the material. For example, in materials with inversion symmetry—those whose structure is the same for an atom at position
In their groundbreaking work, Matteo Rini, Andrea Cavalleri, and coauthors showed in 2007 that exciting an IR phonon in the insulating material Pr0.7Ca0.3MnO3 can temporarily distort its orthorhombic lattice.
6
Such lattice modification, in turn, drives the electronic states into a high-conductivity phase that survives for several nanoseconds. The concept of nonlinear phononics was introduced by Cavalleri and coauthors four years later.
7
They showed that one could leverage nonlinear phonon–phonon interactions in La0.7Sr0.3MnO3—an insulating perovskite with a rhombohedral distortion—to manipulate the crystal lattice and electronic structure. They demonstrated the electronic structure change, induced by phonon pumping with laser light, by using time-resolved reflectivity. The nonlinear mechanism prompts phonons to oscillate around new equilibrium positions, as shown in figure
Figure 2.

Energy configuration in a material. (a) The black dots represent the ground state. The presence of laser light modifies the material’s energy configuration and effectively produces a new ground state. (b) When a Raman phonon is excited by a laser beam, it shifts the energy minimum, produces a distorted lattice, and elicits new behavior. The blue dots illustrate the relaxation of the material (in progress) to a new energy minimum.
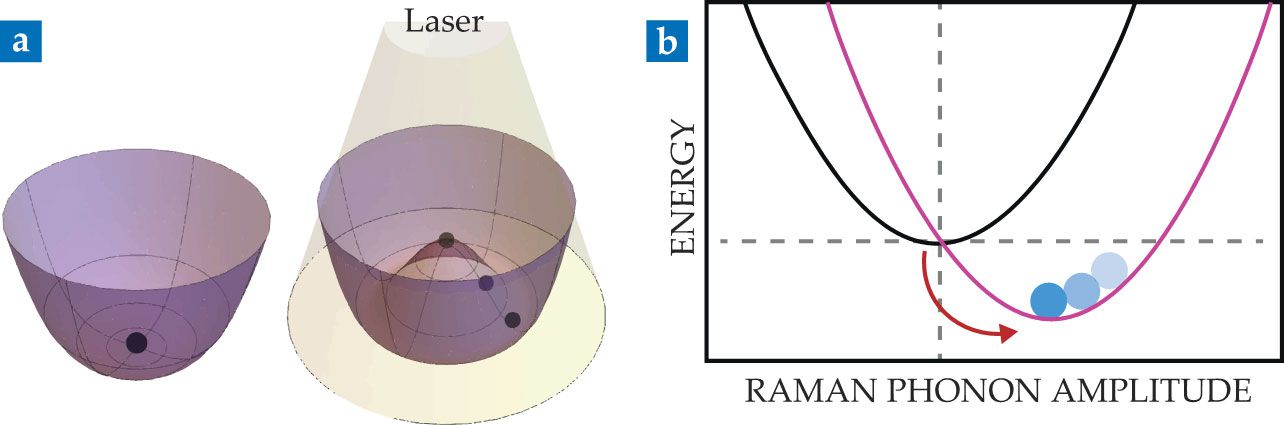
Ferroelectrics compose an important class of quantum materials with ordered states. They possess a nonzero electrical polarization vector along a crystal axis at low temperatures. That ordered state has many applications, including energy harvesting and storage and ultrasound medical devices. One can also manipulate ferroelectric states using electric fields. But the switching rates from such fields are modest. To overcome that problem, researchers can turn to ultrafast lasers. Cavalleri, Roman Mankowsky, and colleagues 8 applied intense laser pulses in resonance with an IR phonon on lithium niobate at about 20 THz. Time-resolved second-harmonic-generation measurements—a technique sensitive to inversion symmetry breaking—showed that the polarization switches direction for 0.2 ps before reverting to its initial state. That capability opens a new ultrafast switching route for ferroelectrics.
In the search for a longer-lived effect in ferroelectric order, Cavalleri’s team also considered strontium titanate, an incipient ferroelectric. 9 As a function of applied strain, the compound transforms into a ferroelectric state. The lower the temperature, the lower the strain required for the transition. In their experiment, the researchers irradiated the sample with 20 THz femtosecond laser pulses in resonance with an IR phonon and tracked the time-dependent second-harmonic-generation signal. Their measurements revealed that the light-induced ferroelectric phase lasted for hours.
Irradiating magnets
Magnetism is perhaps the correlated electronic state people encounter most in everyday life. Storage and manipulation of information is one of the most relevant applications of magnetism in modern society. To that end, controlling the magnetic order by means other than magnetic fields has intrinsic appeal. It can increase information processing speeds and decrease device sizes. Nonlinear phononics could provide such a path, and recent experiments have already shown encouraging results.
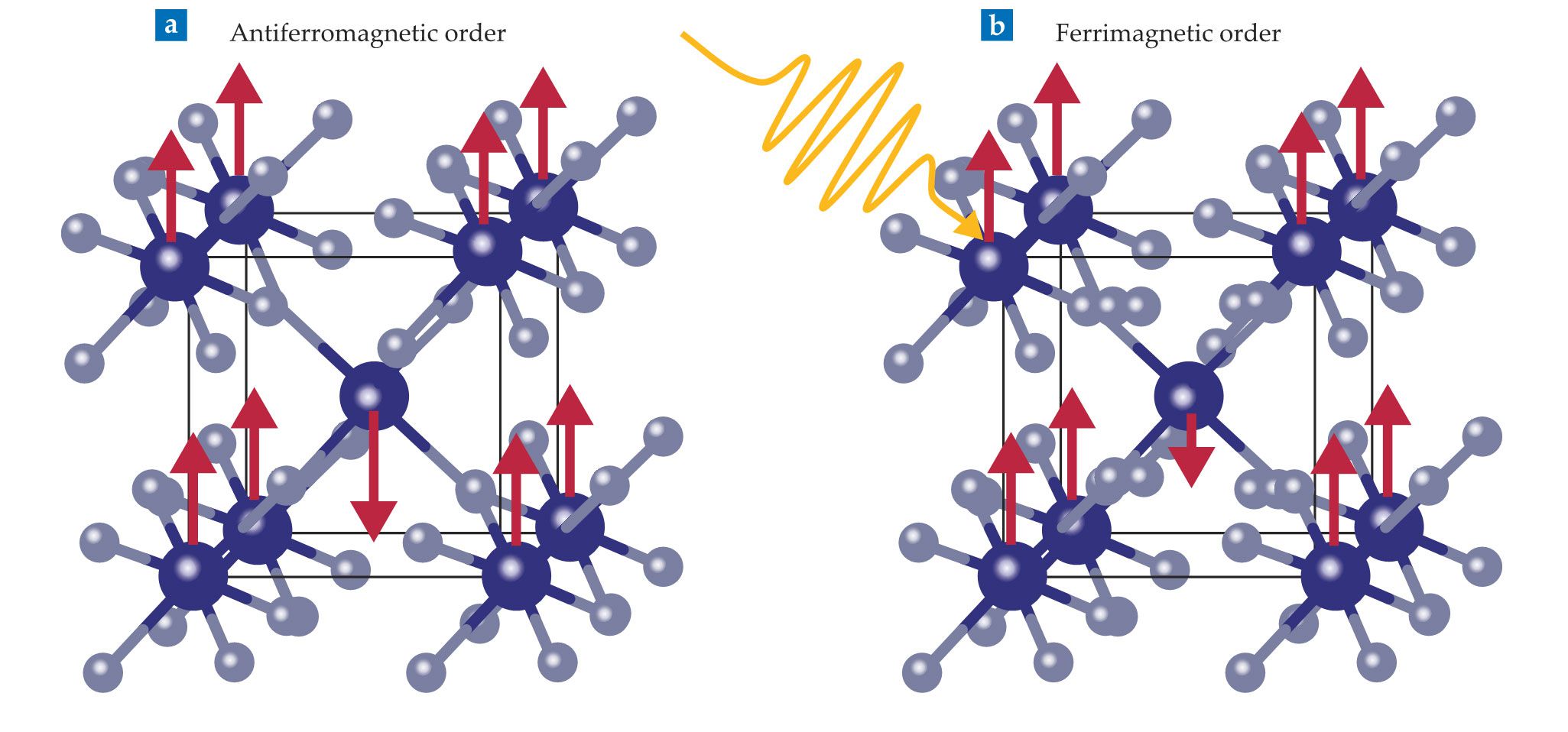
Ankit Disa and colleagues considered the antiferromagnet cobalt fluoride.
10
The crystal’s piezomagnetism is what makes it so intriguing. Under applied stress, the crystal acquires a net magnetic moment. Figure
Figure 3.
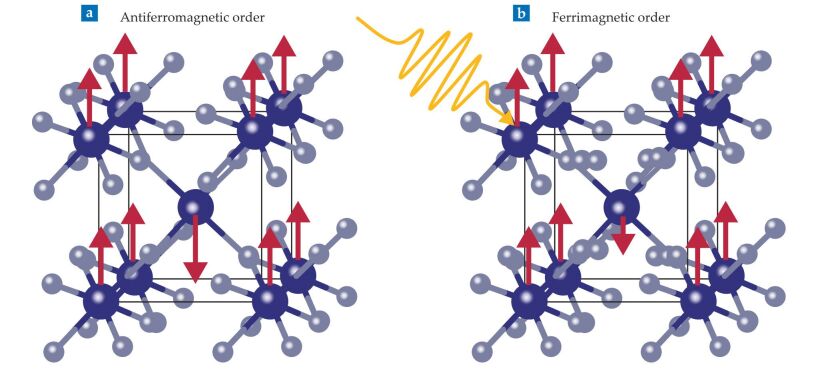
An antiferromagnet becomes ferrimagnetic under laser light. (a) Cobalt fluoride is normally antiferromagnetic at equilibrium, with magnetic moments (red arrows) that are spin up at corner sites and spin down in the center of its unit cell. The net magnetic moment is zero. (b) In its laser-induced distorted lattice, CoF2 becomes ferrimagnetic, with magnetic moments that are both spin up and spin down, but whose net magnetic moment is now finite. The displaced atoms (relative to the antiferromagnetic lattice) produce that net moment.
Dmytro Afanasiev and colleagues examined dysprosium ferrite (DyFeO3) as a function of temperature. 11 The material is a complex magnetic system with multiple magnetic phases. Driving an IR phonon in its lattice to large amplitude can nonlinearly excite a Raman mode that modifies the magnetic interactions between the transition metal and rare-earth ions. Consequently, Afanasiev and coworkers achieved an antiferromagnetic-to-weakly-ferromagnetic phase transition.
Andrzej Stupakiewicz and colleagues achieved an elusive switching of magnetization states through ultrafast phonon excitation. 12 They took thin films of yttrium iron garnet, a ferrimagnet widely used in today’s technology, and irradiated it with IR laser pulses. The initial magnetic configuration, whose magnetic moments aligned with one of the cubic symmetric axes, transformed into a switched four-domain pattern. The magnetization switching mechanism is associated with the excitation of phonons, which produces macroscopic strains in the material.
Although by no means exhaustive, those experiments exemplify the high degree of control over correlated states that one can access by using ultrafast lasers. The next natural step in the control of quantum materials is to look for analogous phonon control of topological states. James McIver and coauthors used ultrafast laser pulses to induce a more general phenomenon, an anomalous quantum Hall state in graphene 13 —an exotic state of matter in which conducting states appear on the edge of the material and the bulk is insulating.
Unlike the examples we just discussed, graphene is a gapless semiconductor (see the article by Andrey Geim and Allan MacDonald, Physics Today, August 2007, page 35
Theoretical aspects
All the experiments described above have motivated the research community to redouble their efforts to understand quantum materials out of equilibrium and to devise theoretical tools to explain the observations. They are also likely to empower researchers to predict new states achievable under a laser drive.
The current theory of nonlinear phononics is based on a combination of group theory and first-principles calculations.
15
Group theory allows for the symmetry classification of phonons and provides the symmetry-allowed interaction terms between the phonons that define the potential energy. And first-principles calculations provide the phonon energetics, such as their frequencies and anharmonic interaction strengths (see the article by Andrew Zangwill, Physics Today, July 2015, page 34
To determine the lattice dynamics, researchers solve a set of differential equations derived from the symmetry-constrained energy potential, including the driving term introduced by the laser interaction with the IR phonons. The solutions describe the transient lattice distortions. First-principles calculations help to determine the new electronic ground state provided the electrons relax much faster than the lattice does and follow that relaxation adiabatically. Besides providing the theory for the experiments discussed earlier, the approach has produced predictions that await experimental verification. 15
More accurate simulations of light-induced effects in quantum materials could be achieved by using frameworks that are based on time-dependent density functional theory 16 or extensions of it. Current theoretical efforts, such as the Octopus project at the Flatiron Institute in New York City and the SALMON project at the University of Tsukuba in Japan, are focused on the real-space computation of light-matter interactions. Those first-principles approaches could, at least in principle, capture the dynamics of all the relevant interacting degrees of freedom and provide accurate descriptions of light-induced effects with increased predictive power. Such schemes are computationally expensive, though, and limited by system sizes and simulation time scales.
Challenges ahead
One of the major challenges facing people who study quantum materials out of equilibrium is identifying potential candidates with desirable responses from the vast number of materials that can be controlled with light. Generalizations to magnetic materials provide even more candidates to consider for phonon control of topological electronic states. 17 But predicting systems that are likely to exhibit other correlated or topological states, such as charge density waves and topological superconductors, remains difficult. As we mentioned earlier, most strongly correlated materials are introduced into the literature on a case-by-case basis. For example, recent experiments by Stephen Wilson’s group at the University of California, Santa Barbara, showed that CsV3Sb5 has topological electronic bands in its normal state. At low enough temperatures (around 2.5 K), however, it becomes a superconductor. The next step might be to induce dynamical transitions between the material’s topological and superconducting states by using nonlinear phononics.
The integration of advanced, time-dependent density functional theory calculations with machine-learning approaches could provide a path to extend the time scales and system sizes that researchers can simulate. Molecular dynamics and spin dynamics simulations have already been integrated with deep-learning frameworks to access large system sizes.
On the experimental side, the lasers used in such experiments as magnetization switching 12 require specialized facilities, such as the FELIX (free-electron lasers for infrared experiments), an international user facility that houses two accelerators in Nijmegen, the Netherlands. Even in the present state of laser technology, the field has experienced rapid progress over the past 15 years in ultrafast light-induced control of ordered ferroelectric and magnetic states. Experimental advances could soon extend to other correlated and topological states in recently synthesized materials, such as those with weak van der Waals interactions between layers. 18 Furthermore, the flexible control of a lattice by phonon manipulation promises to unlock new functionalities from materials in out-of-equilibrium contexts, in which new phases of matter could emerge. Shaken is indeed different.
References
1. P. Anderson, Science 177, 393 (1972). https://doi.org/10.1126/science.177.4047.393
2. D. Fausti et al., Science 331, 189 (2011). https://doi.org/10.1126/science.1197294
3. B. Bradlyn et al., Nature 547, 298 (2017); https://doi.org/10.1038/nature23268
M. G. Vergniory et al., Nature 566, 480 (2019). https://doi.org/10.1038/s41586-019-0954-44. M. Imada, A. Fujimori, Y. Tokura, Rev. Mod. Phys. 70, 1039 (1998). https://doi.org/10.1103/RevModPhys.70.1039
5. J. Maciejko, G. A. Fiete, Nat. Phys. 11, 385 (2015). https://doi.org/10.1038/nphys3311
6. M. Rini et al., Nature 449, 72 (2007). https://doi.org/10.1038/nature06119
7. M. Först et al., Nat. Phys. 7, 854 (2011). https://doi.org/10.1038/nphys2055
8. R. Mankowsky et al., Phys. Rev. Lett. 118, 197601 (2017). https://doi.org/10.1103/PhysRevLett.118.197601
9. T. F. Nova et al., Science 364, 1075 (2019). https://doi.org/10.1126/science.aaw4911
10. A. S. Disa et al., Nat. Phys. 16, 937 (2020). https://doi.org/10.1038/s41567-020-0936-3
11. D. Afanasiev et al., Nat. Mater. 20, 607 (2021). https://doi.org/10.1038/s41563-021-00922-7
12. A. Stupakiewicz et al., Nat. Phys. 17, 489 (2021). https://doi.org/10.1038/s41567-020-01124-9
13. J. W. McIver et al., Nat. Phys. 16, 38 (2020). https://doi.org/10.1038/s41567-019-0698-y
14. M. M. Otrokov et al., Nature 576, 416 (2019). https://doi.org/10.1038/s41586-019-1840-9
15. A. Subedi, A. Cavalleri, A. Georges, Phys. Rev. B 89, 220301(R) (2014); https://doi.org/10.1103/PhysRevB.89.220301
D. M. Juraschek, P. Narang, Science 374, 1555 (2021). https://doi.org/10.1126/science.abm008516. E. Runge, E. K. U. Gross, Phys. Rev. Lett. 52, 997 (1984). https://doi.org/10.1103/PhysRevLett.52.997
17. Y. Xu et al., Nature 586, 702 (2020). https://doi.org/10.1038/s41586-020-2837-0
18. E. Y. Andrei et al., Nat. Rev. Mater. 6, 201 (2021). https://doi.org/10.1038/s41578-021-00284-1
More about the authors
Martin Rodriguez-Vega is a Director’s Fellow at Los Alamos National Laboratory in New Mexico. Maia Vergniory is an associate researcher at the Max Planck Institute for Chemical Physics of Solids in Dresden, Germany, and a researcher at the Donostia International Physics Center in Spain. Greg Fiete is a professor of physics at Northeastern University in Boston, Massachusetts.







