Quantum computing with neutral atoms

In 1982 Richard Feynman conceived of a “quantum mechanical computer.” ¹ His central idea was that a quantum device could take advantage of quantum entanglement and superposition to make calculations that are impossible on a classical computer. Two descendants have emerged from that conception: quantum simulation and quantum computing.

In a quantum simulator, one quantum system is used to model the behavior of a different quantum system. For the past 15 years, quantum simulators have taken advantage of the simplicity and controllability of ultracold atoms and ions to study a wide range of many-body physics, including aspects of Hubbard models, quantum magnetism, superconductivity, and the solutions to many other quantum models, both previously conceived and newly invented. A quantum computer is conceptually akin to a digital classical computer, with classical bits replaced by quantum bits, called qubits, that can exist in superpositions of states and can be mutually entangled. The requirements for a quantum computer are more demanding than those for a quantum simulator, so in contrast to quantum simulation, experimental quantum computing is still in its infancy.

Quantum computing seeks to solve numerical problems using a sequence of logic gates, which can operate on either one or two qubits at a time and change their states. Although any calculation that can be performed on a classical digital computer could also be performed on a quantum computer, doing so would be foolish for most problems. It is much harder to manipulate and measure qubits than it is bits. But hard computational problems exist for which no efficient classical algorithms are known. Quantum computing took off as a field of study in 1994 when applied mathematician Peter Shor (then at Bell Labs) showed that a quantum computer could be used to efficiently factor large numbers, a problem whose classical intractability is behind most modern cryptography schemes. Dozens of quantum algorithms have since been developed, with applications to database searching, pattern classification, multivariate optimization, and solving large systems of coupled equations.

Within a year of the promulgation of Shor’s factoring algorithm, scientists demonstrated the first quantum gate at NIST using two trapped ions as qubits. ² The necessary attributes of qubits are well understood. Qubits must be well isolated from the environment to prevent decoherence of their fragile quantum state. They must be prepared with high fidelity—that is, the actual state must closely resemble the intended state. And they must be accurately measured. Finally, to reliably implement any quantum code—that is, to make a universal quantum computer—quantum error correction must be incorporated into qubit memory and gate operations (see Physics Today, February 2005, page 19 ).

For the past 20 years, researchers have been racing to build systems of entangled qubits to meet those challenges. Despite remarkable experimental developments, no one has yet built a quantum computer that can perform a calculation that cannot be simulated on a classical computer. The achievement would take about 50 qubits and about 10⁴ gates. And even that would fall far short of what is needed to factor a classically intractable number. Nonetheless, a handful of physical platforms have emerged as prime contenders for quantum-computing hardware. They include trapped ions, superconductors, neutral atoms, photons, quantum dots, and spins in solid-state hosts. ³ (See, for example, the article by Ignacio Cirac and Peter Zoller, Physics Today, March 2004, page 38 .)

Each of those platforms has proven capable of basic quantum-logic operations, albeit with varying degrees of fidelity. Recent experiments with about 10 qubits in ion and superconducting systems, for example, have demonstrated multiparticle entanglement, small-scale quantum algorithms, and partial quantum error correction. Progress across the board has been such that not only are governments worldwide investing heavily in quantum science and technology, but private corporations have taken notice. R&D is under way at major information technology companies, including Microsoft, Google, Intel, and IBM, and at several smaller companies. (One company, D-Wave, sells devices specifically marketed as quantum computers. The degree to which the devices use quantum entanglement to solve problems is debatable, but they are clearly not universal quantum computers because they do not allow for complete control of the quantum state of individual qubits.)

Although all aspects of qubit manipulation need improvement, scaling up to larger numbers of qubits is a central challenge. Unlike in classical computers, whose bit overhead for error correction is a few tens of percent, error correction schemes in quantum computers require that each logical qubit be encoded in an ensemble of as many as 100 physical qubits. It is beyond the scope of this article—and our threshold for controversy—to compare the many ideas for scaling in each qubit platform. Instead, we describe the state of the art of neutral-atom quantum computing and try to offer a sense of why we think that platform is especially promising from the perspective of scalability.

As qubits, neutral atoms boast several attractive features. They are all identical and can readily be prepared by optical pumping in well-defined initial states. Their qubit states can be precisely measured using fluorescence. And in some cases they can be well isolated from the environment, which allows for long decoherence times; last year, more than seven seconds was demonstrated for an array of single atoms. ⁴ The qubit states can also be rapidly and accurately controlled with electromagnetic fields. Most notably, many atoms can be trapped in close proximity without affecting each other’s quantum states unless they are called on to do so.

Trapping single atoms

Several research groups trap neutral atoms using either magnetic fields or light, but light traps have received the most attention for quantum computing. Atoms are polarizable, and the oscillating electric field of a light beam induces an oscillating electric dipole moment in the atom. The associated energy shift in an atom from the induced dipole, averaged over a light-oscillation period, is called the AC Stark shift.

When the light frequency is detuned from an atomic resonance, little spontaneous emission occurs and the light creates a conservative potential for the atoms. Atoms are attracted to light below the resonance frequency (red detuned) and repelled by light above it (blue detuned). The AC Stark shift is proportional to the light’s intensity. Thus the shape of the intensity field is the shape of an associated atom trap.

The simplest light trap, called an optical tweezer, is a red-detuned laser beam that holds atoms at its focus. Arrays of optical tweezers have been created using both conventional and holographic optics. They can also be made in the form of an optical lattice, whose sites are the nodes or antinodes of a standing wave produced by coherent light interfering with itself. To date, one-, two-, and three-dimensional arrays, such as the ones shown in figure 1, have each trapped up to 50 individual atoms in apparatuses designed for quantum computing. That’s a large number for present-day qubit systems, but there is clearly room to grow. Given a typical 5 µm spacing between sites, ten thousand atoms can be trapped in a 0.5 mm 2D array, and a million atoms can be trapped in a 0.5 mm 3D array. The possibility of such dramatic scaling is at the root of our optimism about using neutral atoms as qubits.

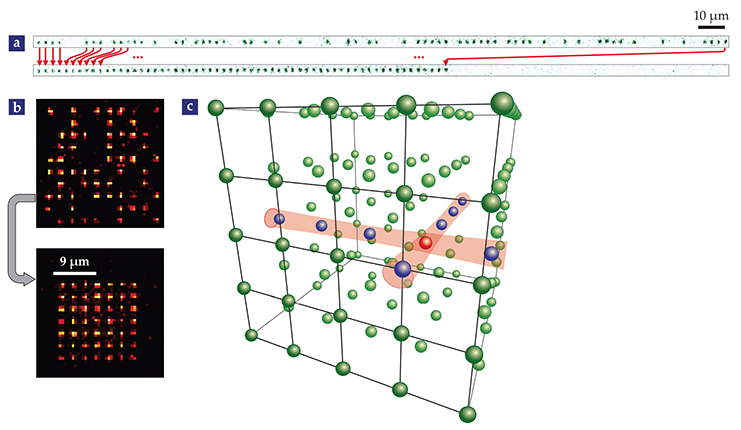
The first step in trapping atoms is almost always laser cooling them to microkelvin temperatures. Conveniently, spontaneous emission during the cooling process scatters light, which can be imaged to detect individual atoms.

But as an array of traps is being loaded with atoms, the cooling light tends to cause atoms at the same site to collide in pairs with each other and be kicked out of the array, which leaves a random half of the traps empty and half of the traps filled with exactly one atom. As long as the vacancy locations are known, it may be possible to reconfigure a quantum computation to account for them. But such a reconfiguration might itself require a quantum computer, so the preference is to start with exactly one atom in every trap.

One elegant way to help achieve a filled array is to start with a Bose–Einstein condensate and then slowly turn on an optical lattice. As the potential wells of the lattice deepen, the atoms undergo a transition from a superfluid to a Mott-insulator state, with one atom per site. The drawbacks of that approach are that nonzero initial temperatures can lead to vacancies, and the intersite atomic tunneling required for the transition works best in a lattice whose sites are more closely spaced than is typically desired for quantum-computing schemes. Another way is to use additional laser beams to suppress the loss of colliding atoms, a technique that can fill up to 90% of the sites in an array. ⁵ But perhaps the most promising approach is to determine where the vacancies are and then rearrange the atoms to completely fill them and thus form a smaller but filled array.

Several labs are starting to rearrange atoms. At Harvard University, Mikhail Lukin and colleagues filled a 60-site 1D optical-tweezer array by turning off the empty traps and moving the filled ones next to each other ⁶ (see figure 1a). At the Institut d’Optique near Paris, Antoine Browaeys and colleagues used a mobile optical tweezer to shuttle 50 atoms among sites in a 2D tweezer array ⁷ (see figure 1b). At the University of Bonn, Andrea Alberti, Dieter Meschede, and their colleagues combined site-selective atomic-state changes and state-selective translations of the lattice potentials to adjust the spacings between atoms in a 1D optical lattice. ⁸ At the Pennsylvania State University (PSU), one of us (Weiss) is pursuing a similar site- and state-selection scheme in three dimensions, in which the number of required steps scales efficiently, as the cube root of the number of atoms.

One unique and inconvenient difficulty presented by neutral atomic qubits is that they are vulnerable to collisions with residual background-gas atoms that knock them out of their traps. Those collisions occur about once every 100 seconds per atom in a standard room-temperature vacuum system. Lifetimes that exceed tens of minutes are possible in cryogenic vacuum systems. Infrequent atom loss, like other qubit errors, can be repaired with quantum error correction, by using atom-rearrangement hardware to replace a lost atom.

The final step in preparing atom qubits for a computation will likely be some variant of sideband laser cooling. That technique was first invented for trapped ions (see Physics Today, October 2005, page 24 ) and can cool atoms to their vibrational ground state up to 90% of the time, ⁹ cold enough for most quantum-computing schemes. It is no doubt possible to start even colder; however, to handle the inevitable heating that will arise in a long quantum computation, it may be necessary to transfer quantum states to other cold atoms while the original atoms are being recooled.

Quantum gates

Measurement accuracy, controllability, and the fact that all atoms of one species are identical constitute major strengths of atom- and ion-based quantum computing. Those strengths are well known in the context of atomic clocks, and they account for the clocks’ superlative precision. In fact, viewed from the perspective of quantum computing, atomic clocks are built from single-qubit gates implemented in parallel on a large ensemble of atoms.

However, making precise single-qubit gates for a quantum computer requires the ability to execute operations on individual atoms. It also requires eliminating any cross talk, which can change the quantum states of nearby, untargeted atoms. One way to achieve that level of control is to drive atomic transitions between hyperfine levels using laser beams that are tightly focused on individual atoms. Such a gate can be fast—on the scale of a microsecond or less—and can have high fidelity if the light intensity is sufficiently stable. Another way is to drive atomic transitions with more easily controlled microwaves. Because microwave wavelengths are far too large to distinguish individual atoms, the atoms must be addressed by selectively shifting their resonance frequencies, either with magnetic fields or focused laser beams. Using crossed laser beams and a sequence of microwave pulses, one can reach into a 3D ensemble to perform a gate on a target atom without cross talk, as exemplified in box 1. Because single-qubit gate times range from fractions of a microsecond to a few hundred microseconds, as many as 10⁵ gates can be performed within the longest demonstrated decoherence times.

Figure 2 illustrates a series of targeted single-qubit gates acting on a 3D array of cesium atoms, each of which is put in a quantum superposition of two hyperfine states. The experiment, which produces the letters P, S, and U in a fluorescent pattern, demonstrates independent control over atoms at all 125 lattice sites, which (given 40% site occupancy) amounts to 50 qubits at a time.

A two-qubit gate, which creates entangled states on demand, requires strong interactions among qubits. But neutral atoms in their electronic ground states interact weakly—the very reason they can be packed close together in a quantum computer. One solution is to temporarily move atoms so closely together that they experience a “controlled, cold collision.” ¹⁰ When using that approach, however, it is difficult to control the moving traps and the motional states of the atoms accurately enough to produce a high-fidelity gate. A more widely pursued solution, proposed nearly two decades ago by Dieter Jaksch (now at Oxford University) and colleagues in a seminal paper, ¹¹ is to temporarily transfer atoms to Rydberg states, in which an electron is excited far from the atomic nucleus.

Rydberg atoms have strong mutual dipolar interactions. Indeed, the interaction between two Rydberg atoms separated by 5 μm and with principal quantum number n = 100 is about 12 orders of magnitude larger than that between ground-state atoms. The strong interaction produces a so-called Rydberg blockade—a phenomenon analogous to the well-known Coulomb blockade, by which only one electron at a time can move through a narrow channel. The Rydberg blockade prevents more than one atom in a small volume from being simultaneously excited to a Rydberg state. For instance, if an atom is excited to a Rydberg state, an attempt to excite a second, nearby atom with the same laser frequency will fail, because the long-range interaction between the atoms shifts the resonance condition for excitation of the second atom. The upshot: The blockade interaction can entangle two or more nearby qubits using a simple three-pulse sequence, as explained in box 2.

Research groups ¹² at the University of Wisconsin–Madison and at the Institut d’Optique first demonstrated entanglement between individual rubidium atoms in hyperfine ground states using a Rydberg blockade in 2010. (See Physics Today, February 2010, page 13 , and February 2009, page 15 .) The initial experiments just barely passed the threshold between separable and entangled states. Since then, experimental improvements and variations on the basic entanglement protocol ^{13 , 14} have led to entanglement fidelities of about 75%. That’s well below what has been achieved with trapped-ion and superconducting qubits. But the fidelities are likely to improve when ground-state cooling and other advancements are incorporated into Rydberg gate experiments.

Another issue that can affect fidelity is the extreme sensitivity of atomic Rydberg states to background electric fields created by charge fluctuations in an experimental apparatus. Future advances may require better ways of mitigating those fields or the Rydberg state’s sensitivity to them. A more intrinsic difficulty is a Rydberg state’s finite radiative lifetime, which leads to decoherence during a gate operation. Obtaining optimal fidelity will be a trade-off between radiative decay when the gate is too slow and a compromised blockade when the gate is too fast. A recent numerical optimization of pulse shapes to minimize off-resonant excitation, even for fast 50 ns gates, ¹⁵ has shown the feasibility of achieving 99.99% entanglement fidelity. Such performance is a prerequisite for implementing error correction.

Error correction requires measuring the states of selected atoms without disturbing the quantum states of their neighbors. Several possible approaches take advantage of the flexibility of cold-atom experiments. For instance, two Rydberg-interacting atomic species could be used, one for storage and one for measurement. Or optical shielding techniques could be used to protect qubits that are not being measured. Those and other ideas are just starting to be developed, ¹⁶ so truly scalable quantum computation remains a problem to be tackled in the next generation of experiments.

Perspective

From the view of an experimental physicist, the task of exerting precise control over a large number of individual quantum particles is a grand challenge. A quantum computation requires preparing atoms in well-defined quantum states, controlling the atoms’ interactions to carry out logical operations, and measuring the resulting states to extract the computational result—all while maintaining near-perfect isolation from the environment. The technical achievements needed to meet that challenge are likely to reap a broad range of benefits beyond the central goal of quantum computing.

For instance, advances in neutral atom quantum computing may broaden the capabilities of metrology and time keeping. Atomic clocks already operate with exceedingly low uncertainties, near one part in 10¹⁸. At the frontiers of clock research are efforts to introduce entanglement and quantum-logic protocols to circumvent the standard quantum limits for uncorrelated particles. ¹⁷ The ability to create, control, and probe many-particle quantum states with high precision will enrich the experimental study of quantum mechanics at the border between classical and quantum dynamics.

As for the central goal, we anticipate that over the next five years several qubit platforms, including neutral atoms, are likely to reach a sufficient size and fidelity that they can perform quantum calculations that cannot be modeled on a classical computer. It is much harder to predict how long it will take before a quantum computer is able to factor intractably large numbers.