Polariton condensates
DOI: 10.1063/1.3480075
Most students of physics know about the special properties of Bose-Einstein condensates (BECs) as demonstrated in the two best-known examples: superfluid helium-4, first reported in 1938, 1 and condensates of trapped atomic gases, first observed in 1995. 2 (See the article by Wolfgang Ketterle in Physics Today, December 1999, page 30 .) Many also know that superfluid 3 He and superconducting metals contain BECs of fermion pairs. 3 An underlying principle of all those condensed-matter systems, known as quantum fluids, is that an even number of fermions with half-integer spin can be combined to make a composite boson with integer spin. Such composite bosons, like all bosons, have the property that below some critical temperature—roughly the temperature at which the thermal de Broglie wavelength becomes comparable to the distance between the bosons—the total free energy is minimized by having a macroscopic number of bosons enter a single quantum state and form a macroscopic, coherent matter wave. Remarkably, the effect of interparticle repulsion is to lead to quantum mechanical exchange interactions that make that state robust, since the exchange interactions add coherently. 3 , 4
In the past few years, researchers have discovered a new type of BEC based on the polariton—a quasiparticle that is a quantum mechanical superposition of a photon and an electronic excitation in a solid. Polariton condensates have now been shown to exhibit the classic hallmarks of a BEC, including a bimodal momentum distribution, 5 , 6 quantized vortices, 7 spontaneous symmetry breaking, 8 long-range coherence, 9 phase locking, 10 and long-range superfluid motion. 11 Polaritons are less familiar than other bosonic quasiparticles, despite having been introduced conceptually by John Hopfield many decades ago and observed experimentally in both bulk-solid and quantum-well semiconductor structures. Since the 1990s, however, designs of semiconductor microcavities that confine the quasiparticles to a two-dimensional sheet have allowed dramatic progress in controlling and observing polariton condensates. The field has moved rapidly from demonstrations of collective, driven many-body states to polariton trapping to the spontaneous condensates we discuss here. The early work is nicely summarized in reference .
A new eigenstate
Figure 1(a) shows a typical structure for polariton experiments. One or more semiconductor layers are used as quantum wells. The polariton effect will occur with just one quantum well, but most recent experiments insert extra, identical quantum wells to increase the overall coupling. In the thin quantum-well layers, the charge carriers (electrons and holes) are confined to 2D motion. The quantum wells are then placed between two mirrors, typically made of alternating dielectric layers in a Bragg reflector structure; the arrangement makes an optical cavity that also restricts photons to 2D motion.
Figure 1. A microcavity polariton experiment. (a) The setup consists of one or more quantum wells (QW) placed at the antinodes of a confined optical mode in a cavity. Typically, the entire structure is made as a single solid-state device, with the mirrors of the cavity made of alternating dielectric layers—a structure known as a distributed Bragg reflector (DBR). (b) When coupled in a quantum well, the exciton and photon modes mix and become upper and lower polariton (UP and LP) modes, with the energy difference between them defining the Rabi splitting. Mode energies, E, are shown here as a function of in-plane momentum, k ||. In general, special care must be taken to tune the exciton and photon modes to be nearly resonant at k || = 0.
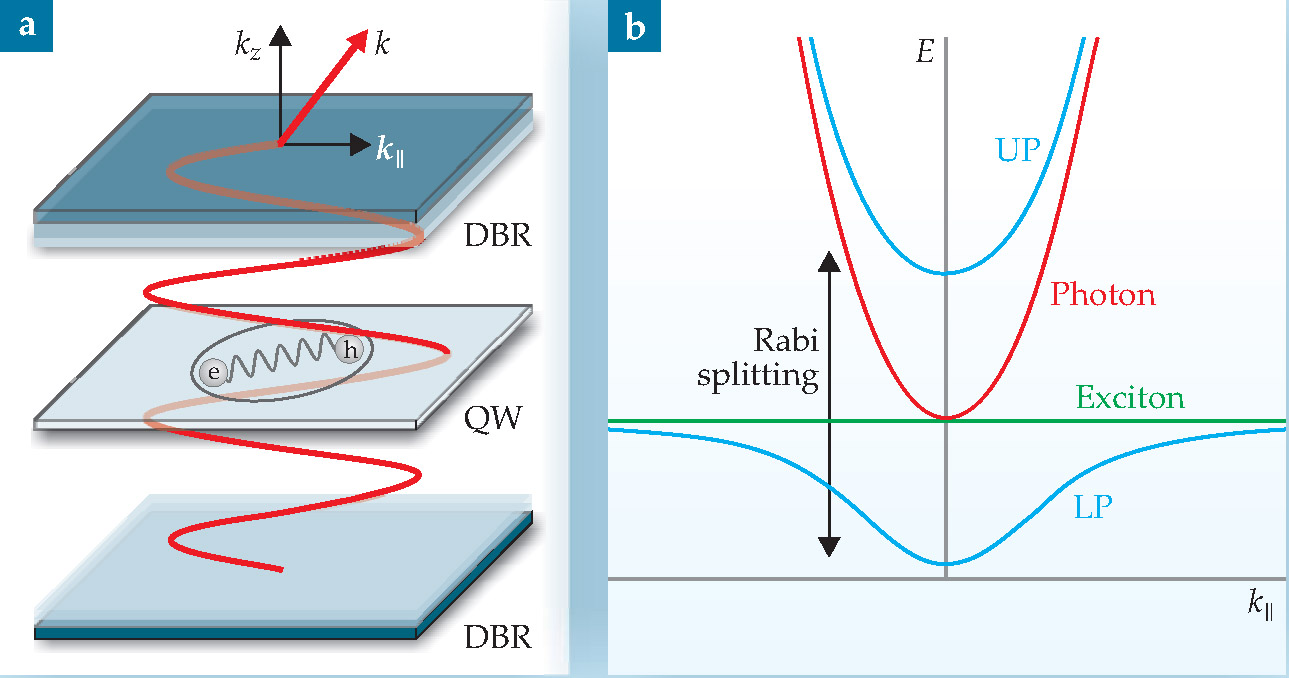
If there were no cavity, then the absorption of a photon by a quantum well at low temperature would yield an exciton—an electron in the conduction band and a hole in the valence band, bound together by Coulomb attraction. An exciton is a composite boson, just like a Cooper pair of electrons in a superconductor, except that it is metastable, since the electron can emit a photon and fall back into the hole. An exciton is analogous to positronium, in that both are particle-antiparticle pairs with finite lifetimes.
If a quantum well is placed at an antinode of the confined photon mode in an optical cavity, and if the energy of the exciton is close to that of a photon in the cavity, then the exciton and photon states couple to each other. As shown in figure
Many people have trouble thinking of polaritons as “real.” But quantum mechanics shows that once the proper eigenstates for a system have been defined, they are the correct particles to keep in mind. Quantum field theory goes further to say that every particle—even familiar ones such as the electron, proton, and photon—can be viewed as an eigenstate, or excitation resonance, of an underlying field. New resonances such as polaritons, magnons, phonons, and so on, known as quasiparticles, are not fundamentally different in character from elementary particles; they are just highly renormalized to have different properties. In particular, polaritons can be viewed as photons having an effective mass and much stronger interactions than photons in a vacuum. Solid-state physics has a long history of generating new types of particles that can be studied as real objects, including particles with fractional charge (as in the famous fractional quantum Hall effect) and quasiparticles that exist only in the presence of other quasiparticles, such as fermion-like excitations of Bose-condensed Cooper pairs in a superconductor.
A brief but eventful existence
No mirror is perfect, so in typical experiments a polariton exists for only 5-20 picoseconds inside an optical cavity before tunneling out to form an external photon. Although that may seem like a short time, it can be much longer than the interparticle scattering time—the relevant time scale to reach a thermalized quasi equilibrium that can be described by statistical mechanics with approximate number conservation. Polaritons at high density in microcavities have strong repulsive elastic scattering interactions, which allow them to thermalize in less than a picosecond.
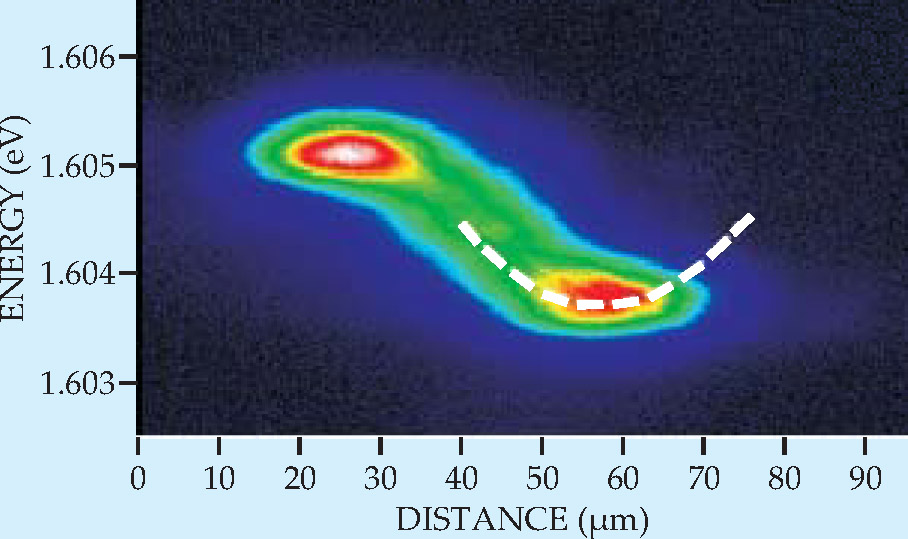
Polaritons can also move from place to place. They have been observed by time-resolved imaging to scatter into a thermal momentum distribution, much like a gas of atoms. And analogous to the way gases of atoms can be trapped in free space by magnetic and optical fields, polaritons can be trapped by various methods in confined regions inside a solid. One such method is to apply a stress with the tip of a pin to shift the bandgap of the semiconductor, creating a potential energy minimum, or “stress trap,” at a point in the solid (see figure 2). Polaritons in the semiconductor can then be made to migrate toward, congregate near, and under certain conditions condense in the trap.
Figure 2. Migrating polaritons. In a stress-trap experiment, polaritons created by a laser at one point in a semiconductor (the bright spot at the top left in this spectral image) flow down an energy gradient and accumulate in an approximately harmonic potential minimum about 35 µm away (the spot at lower right). The potential minimum, indicated here by the dashed white curve, results from a shift in the bandgap of the semiconductor due to stress applied with the tip of a pin. The entire migration happens within the polaritons’ lifetime of around 15 picoseconds, such that the drift velocity is about 108 cm/s.
(Adapted from ref.
A useful feature of planar microcavities is that the in-plane momentum of the polaritons is preserved when they tunnel into photons that leave the sample. Therefore, the momentum distribution of the polaritons, along with the energy spectrum at each momentum, can be measured by resolving the angle of the emission of the external photons. Figure 3(a) shows the momentum-space narrowing—a canonical Bose-Einstein effect—of polaritons condensing as their density increases in a stress trap. (Density can be increased at nearly constant temperature by turning up the intensity of the pump laser.) The spectral energy width also decreases, which indicates increased coherence in the polariton state.
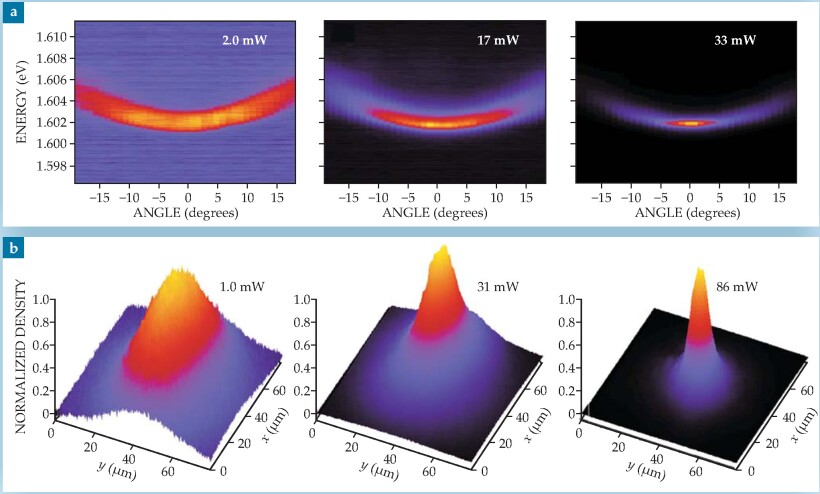
Figure 3. Momentum, energy, and spatial narrowing. (a) The angular distribution of the light emission from polaritons, shown here in angle-resolved spectra, maps directly to the polaritons’ in-plane momentum distribution. At low polariton density or, equivalently, low pump-laser intensity, the thermalized polariton cloud fills a wide range of momentum states. As the pump intensity increases, the density approaches the critical threshold, Bose-Einstein statistics enforce a pileup of the particles near the ground state, and the momentum distribution narrows. The energy width also narrows, which implies increasing coherence. The curvature of the spectra gives the effective mass of the polaritons, via the relation ħ2/m = d 2 E/dk || 2. (b) A similar experiment shows spatial narrowing of a polariton cloud. Although one might expect an increase in the number of particles to lead to higher pressure and a resulting expansion, the opposite happens. As their density is increased past the critical threshold, polaritons pile up in the ground state, causing the polariton cloud to shrink.
(Adapted from ref.
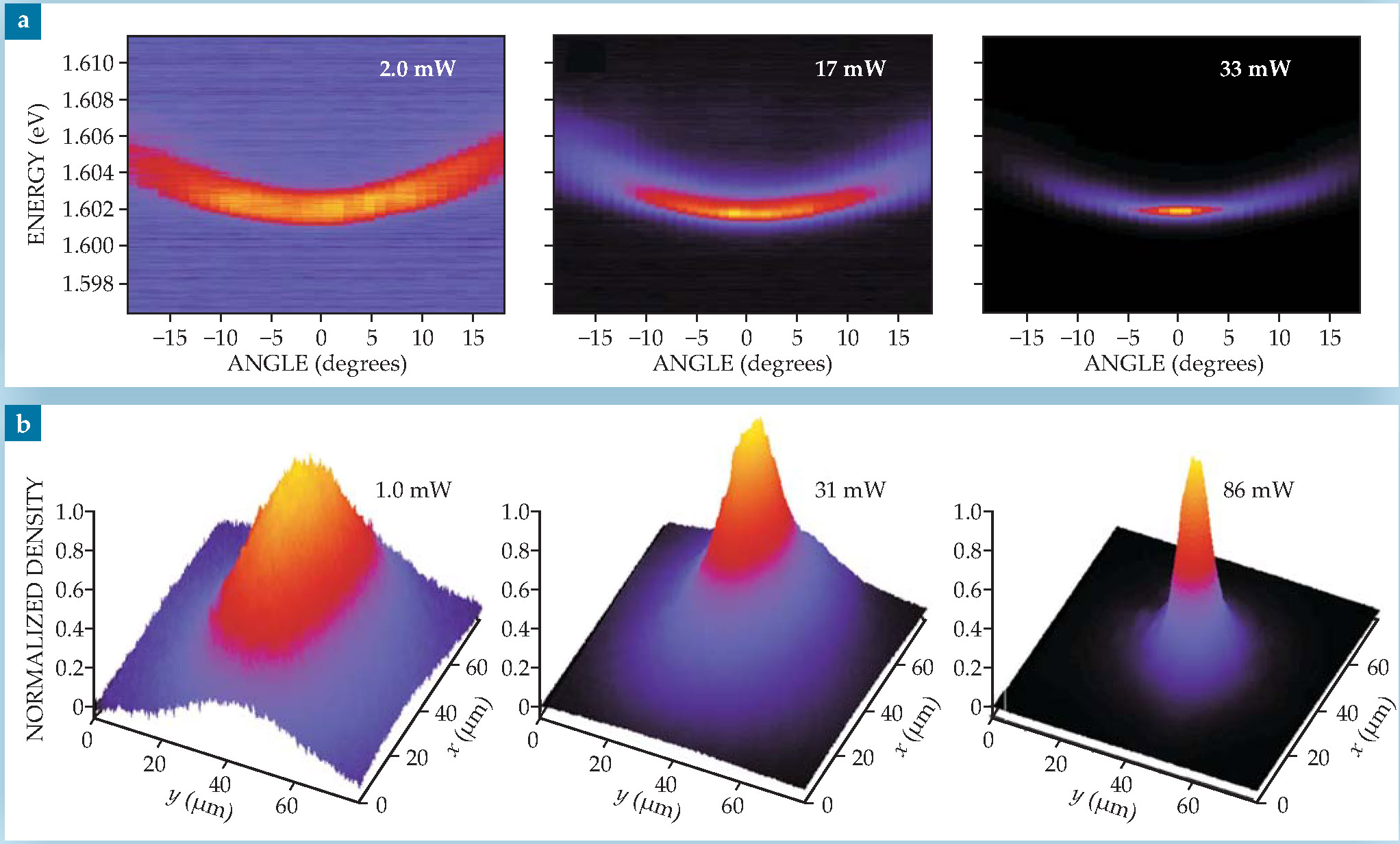
The spatial width of the polariton cloud also narrows as the polaritons increase in density. The polaritons pile into their ground state, and even taking into account the repulsive interactions of the polaritons, their resulting spatial extent is small compared with the size of the cloud of thermal particles in the trap (see figure
Why go to all the trouble to create polaritons in microcavities? As BECs, polaritons belong to the same general class as atomic condensates and superfluid He, yet one feature makes them quite different: They are extremely light—about 10-4 electron masses—and lighter mass means that quantum effects appear at higher temperature.
Recall that the general condition for superfluid coherence is that the thermal de Broglie wavelength of the particles, λ ∼ (h 2/mk B T)
An unconventional laser
Like a laser, a polariton condensate is an open system, continuously pumped in order to support the electron-hole pair density, which in turn supports a coherent light field. In both systems, an incoherent pump creates free electrons and holes, and in each case coherent light is produced in a spectrally narrow, beamlike emission. What, then, is the distinction? The difference, qualitatively, is the degree to which the electronic states participate in the coherence. In a laser, the coherent light adopts the cavity photon mode frequency, which is fixed by the cavity length and dielectric constant. The role of the electronic excitations is both to populate the photon mode and to damp it. Consequently, to produce coherent light, the population of electronic excitations must be inverted, so that stimulated emissions, which yield phase-locked photons, dominate spontaneous emissions, which yield photons of random phase. In contrast, in a polariton condensate, the phases of the exciton and photon are locked together as a coherent polariton, and the phases of the polaritons are in turn locked together as a coherent condensate. Hence the oscillating light field adopts the polariton energy and phase, and there is no need for inversion; coherent fields can be supported by a thermal quasi equilibrium. One practical outcome is that the electron-hole density threshold for coherent emission is much lower than for a conventional laser in the same semiconductor medium. The term “polariton laser” is often used to refer to coherent light emission from a polariton condensate that is not quite in full equilibrium with the noncondensed polaritons.
The polariton system allows a continuous transition between condensate and lasing states. Since the continuous pumping introduces random phase perturbations, the condensed state only forms above a finite polariton density threshold, even at the lowest temperatures.
13
Theoretical estimates made at Cambridge, based on experiments by Benoît Deveaud-Plédran’s group at the École Polytechnique Fédérale de Lausanne in Switzerland, and Le Si Dang’s group at Joseph Fourier University in Grenoble, France, suggest that the onset of the condensed state is determined by losses rather than by temperature. If the pumping further increases the density beyond the critical density for condensation, dephasing eventually decouples the excitonic component from the photon component, the polariton energy splitting (known as the Rabi splitting, see figure
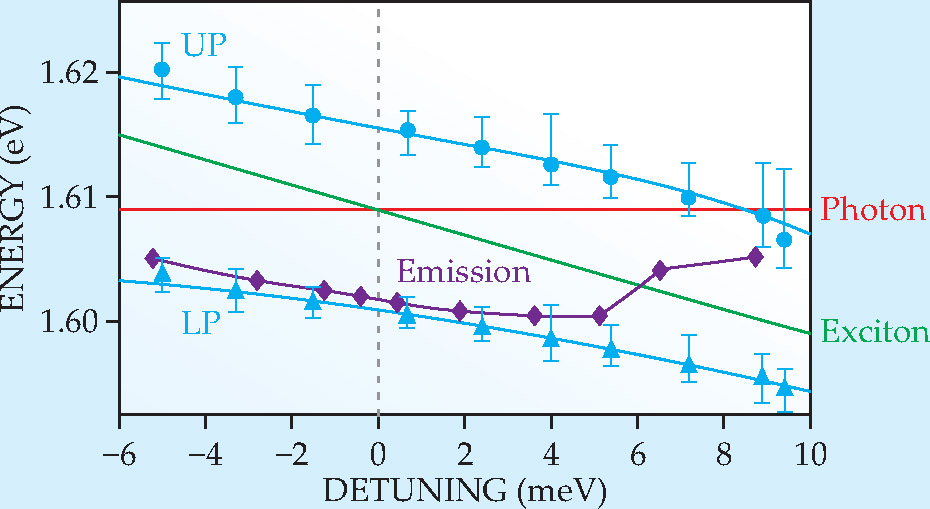
Recent experiments have clearly identified two distinct thresholds—one for polariton condensation and another for standard lasing. 14 , 15 Figure 4 shows data from one of those experiments, in which stress—applied by the tip of a pin, as in the experiments of figures 2 and 3—was used to tune the bandgap energy of the quantum-well excitons relative to the cavity photon energy. The resulting shift in the polariton condensate energy moves in the same direction as the exciton energy shift, which demonstrates that the electronic component is very much involved in the coherence of the condensate. By contrast, in the conventional lasing state, the coherent emission occurs at the cavity photon energy, which does not shift with stress.
Figure 4. A transition between polariton condensate and conventional lasing states. The upper and lower polariton (UP and LP) energies decrease as the exciton energy is tuned—by means of a mechanical stress—through the cavity photon resonance. The stress shifts the electronic states of the medium while leaving the cavity photon energy largely unchanged. The energy of the cavity emission at the threshold for coherence initially decreases like the exciton state, which indicates that the system is a condensate and that the electron states of the medium are involved in the coherence. At large detuning—high stress—the excitons and photons become decoupled, and only standard lasing is possible, so the coherent emission jumps up to track with the cavity photon mode.
(Adapted from ref.
Other unique properties
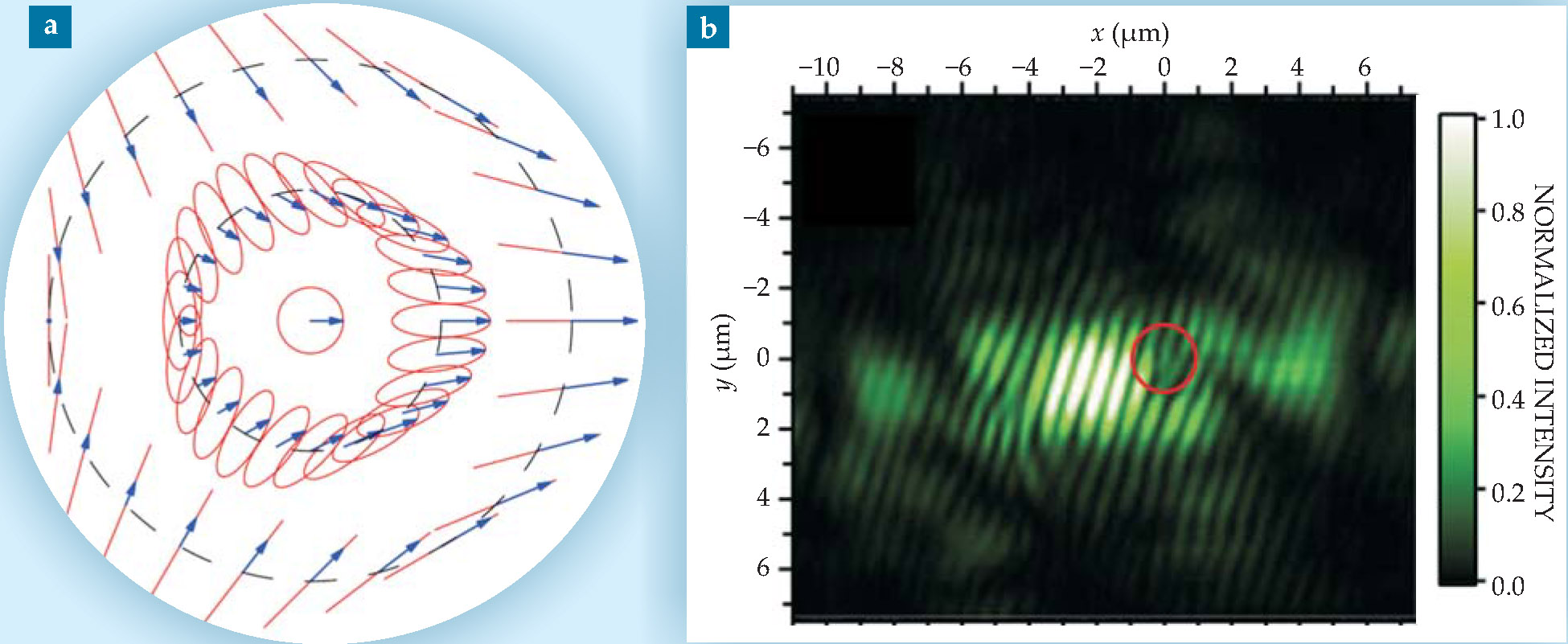
Polaritons in microcavities are 2D, spin-1 bosons with +1 and −1 spin projections, corresponding to left and right circular polarization in their plane of motion. The nonzero angular momentum condensate can therefore support so-called half vortices, which have a π, instead of 2π, rotation in phase along with a π rotation of polarization over the same path around the vortex core. In a fascinating recent experiment by the Lausanne group, half vortices were detected as forks in interference patterns of the light coming from a polariton condensate (see figure 5). 7 The patterns are observable in time-averaged experiments because the vortices are pinned at local structural defects.
Figure 5. “Half vortices” in polariton condensates. (a) In a path around a so-called half vortex—starting, say, at the leftmost point of the outer dashed ring—the phase of the polariton wavefunction rotates by 180°, not 360°. The half-phase rotation is accompanied by a 180° rotation in polarization. In the schematic, red lines and ellipses indicate the polarization; blue vectors—representing an instantaneous field, which over time traces out the wavefunction—indicate the phase. Far from the core the polarization is linear, toward the center it becomes elliptical, and at the core it is circular. (b) Such a vortex can be detected as a fork in the interference pattern that is produced when the polariton condensate light emission is sent through a circular polarizing filter. The fork (circled in red) is seen if the filter passes one handedness, but it is absent if it passes the other, a signature of half vortices.
(Adapted from ref.
Another distinctive trait of polaritons is that their dynamics can be driven externally. In a superconductor, the coherent phase is visible only to another superconductor, via the Josephson effect. In a polariton condensate, the condensate’s phase can be coupled to that of an external coherent source of light. It is therefore possible to create coherent polaritons directly by tuning an external laser to resonate with a polariton mode. Though such a system is not in thermal equilibrium, it shows a type of spontaneous symmetry breaking, in that the coherent oscillation of the polaritons will have a fixed but undetermined phase. Luis Viña’s group at the Autonomous University of Madrid in Spain, along with Maurice Skolnick’s group at the University of Sheffield in the UK, used a resonant external laser to produce superfluid, soliton-like transport 11 and to inject vorticity into a condensate. Well before the demonstration of thermalized condensates, coherent polariton systems generated by resonant pump lasers had also been used to show strong nonlinear effects, 12 and a collaboration between the Viña group and Jacqueline Bloch’s group at the CNRS Laboratory of Photonics and Nanostructures in Marcoussis, France, recently observed critical slowing of polariton dynamics near the symmetry-breaking phase transition in a polaritonic optical parametric oscillator. 16
Polariton energy scales
Polariton condensates—and Bose-Einstein condensates in general—are characterized by several relevant energy scales in addition to the critical temperature, T c, determined by the thermal de Broglie wavelength condition, k B T c ∼ nh 2/m, as described in the text. One energy scale is the average repulsion between particles, of order nU, where n is the particle density, and U is the characteristic interaction energy per unit density. If that energy is small compared with the thermal energy, k B T, the system is weakly interacting; if it is comparable to or larger than k B T, it is strongly interacting. Cold atoms in optical traps and polaritons in microcavities are weakly interacting at typical condensation densities, whereas the atoms in liquid helium are strongly interacting.
Another natural energy scale is the binding energy of the fermions that make up the composite bosons, h 2/µa 2. Here µ is the reduced mass of the fermion pair and a the pair correlation length—the characteristic distance between the fermions that make up the composite boson. For polaritons, µ is on the order of the electron mass—about 104 times larger than the polariton mass—so when the condition for polariton condensation sets in, the excitons are rarely in contact; that is, na 2 « 1. Equivalently, the binding energy is large compared with k B T, so the composite bosons act to all intents and purposes as pure bosons. The same is true for all bosonic atom condensates, including liquid He. If na 2 becomes larger than 1, then in the high-temperature limit a Mott transition to an uncorrelated fermionic plasma will occur, whereas at low temperature a Bardeen-Cooper-Schrieffer transition to a coherent state of weakly correlated fermions can occur (see the article by Carlos Sá de Melo in Physics Today, October 2008, page 45 ). Such behavior describes Cooper pairs in superconductors and can also happen with pairs of fermionic atoms in optical traps.
The preceding energy scales are important for all Bose-Einstein condensates; for polaritons, there are two others. One is the energy of the splitting between the lower and upper polariton states, known as the Rabi splitting (see figure
The final relevant energy scale for polaritons is the energy broadening due to their finite lifetimes. It can be understood simply as the Heisenberg energy uncertainty, ΔE ∼ h/Δt, due to the finite time, Δt, spent in one state. The Q factor—the average number of round trips a photon makes before it escapes through the cavity mirrors—for the polariton microcavity structures is typically 2000 or greater, which means that the lifetime broadening of the cavity mode is much less than the Rabi splitting between the two polariton eigenstates. The polaritons are therefore well-defined particles. That so-called strong coupling is one important distinction between a polariton mode and a conventional laser mode. Nonetheless, polaritons, given their finite lifetimes, are continually lost, and losses generate noise due to the fluctuation-dissipation theorem. Therefore, condensation will not occur at arbitrarily low densities. In the condensed state, losses will also subtly alter the long-wavelength and low-frequency collective behavior of the condensate from that of a true superfluid.
Many polariton experiments do not have a single externally controlled trap, but instead have several traps due to multiple potential minima in a disordered landscape. In a recent experiment, the Lausanne and Grenoble groups observed several coexisting condensates in adjacent local minima. 10 At low density, each condensate in a separate minimum had its own phase. At higher density, when the repulsive interactions of the polaritons caused them to fill up their localized regions and begin to interact with particles in neighboring regions, the separate condensates locked phases. In another experiment, the Sheffield and Grenoble groups observed overlapping condensates with slightly different frequencies and wavefunctions. 9 Such systems contain polariton currents, driven by diffusion and gradients in the potential energy landscape. The nonlinear dynamics of coupled condensates is becoming an interesting area for further research. Since the microcavity polaritons form a truly 2D gas, they may also present opportunities to study the crossover from a trapped condensate with stable phase to a translationally invariant superfluid with strongly fluctuating phase.
The polaritons’ lifetimes are long enough to lead to substantial effects in the excitation spectrum of the polariton condensate. The classic feature of a superfluid is the development of a linear collective sound mode—the so-called Bogoliubov mode—which is predicted to be visible as a shift in the polariton emission spectrum above threshold; Yoshihisa Yamamoto’s group at Stanford University has reported experimental evidence of such a shift. 17 However, theory predicts that polariton condensates will decohere on the longest length scales; that is, the Bogoliubov mode should become diffusive. That length scale is estimated to be long enough that it is not easily visible in current experiments. Still, it is an important fundamental difference from other BECs.
The mathematical picture
Theoretical approaches to the study of polariton condensates fall into three broad classes. 13 At the lowest densities, microscopic models treat polaritons as weakly interacting bosons. As the density increases, the relative proportion of photon to exciton in the ground state grows beyond the low-density 50-50 superposition case. Beyond the crossover to a dense system, it is more convenient to work with models that have an explicit long-range photon-mediated interaction between localized exciton states. Such models are amenable to being treated as open systems coupled to baths and can also readily incorporate the effects of excitonic disorder. That approach allows quantitative connection to experiments and the eventual crossover to standard lasing when, at yet higher densities, the exciton and the photon decouple.
The details of the microscopic models, however, are too cumbersome to describe large-scale spatial structure, and a coarse-grained description of order-parameter structure and dynamics is needed. As is the case with atomic condensates (see the article by Keith Burnett and colleagues in Physics Today, December 1999, page 37 ), a Gross-Pitaevskii or Ginzburg-Landau approach is preferred, 4 but modified to include dissipation, dynamics, and flow. A Gross-Pitaevskii equation is simply a Schrödinger equation for a matter wave, having a potential energy term that is linear with local particle density or, in other words, proportional to the square of the wavefunction, |Ψ|2; a Ginzburg-Landau equation is the time-independent version.
In a Gross-Pitaevskii or Ginzburg-Landau equation, the polariton condensate is treated as a classical wave; the polariton-polariton interactions correspond to a highly nonlinear term in the wave equation. Much of the behavior seen in microcavity polariton experiments with resonant excitation can therefore be interpreted as extreme nonlinear optical effects. For example, optical parametric oscillator effects, including entangled photon pair generation, have been demonstrated in polariton condensates with continuous-wave excitation at low average power; in contrast, standard optical parametric oscillator devices require intense, ultrafast laser pulses. Not all of the polariton experiments can be described by a simple nonlinear wave equation, however, since fluctuations, dissipation, spin flip, and flow can sometimes play a major role.
The polariton express
In the past decade, researchers have attempted experiments on Bose-Einstein condensation of various other types of quasiparticles in solids, including magnons, spin excitations (“tripletons”), long-lifetime excitons in coupled quantum wells, and correlated electron-hole pairs at high magnetic field in coupled quantum wells. 18 All of those, like polaritons, have lifetimes long enough to be described by near-equilibrium statistics.
Researchers in the field of polariton condensates have had to overcome the difficulty of preparing thermalized systems in short time scales, a task complicated by the fact that polariton coupling to the atomic lattice via phonon emission and absorption is weak. Weak coupling makes cooling difficult, since the only avenue available for polaritons to get rid of energy is through phonon emission—vibrational motion of the lattice atoms, which diffuses away. The relatively weak interactions between polaritons and the atomic lattice of the semiconductor may be an advantage, however, in next-generation experiments aimed at studying quantum dynamics in a many-body system.
Polariton condensate work is now expanding and includes a European network of researchers headed by Alexey Kavokin at the University of Southampton, UK. The work promises to lead to unique optical applications and new physics. Coherent polaritons in microcavities have already been used for such nonlinear optical effects as optically gated amplification, optical spin Hall transport, and optical parametric generation of entangled photon pairs. 12 Current work on electrical pumping instead of the widely used optical pumping may open a further array of potential applications, such as low-threshold coherent light generation, optical transistors (modulation of one light beam by another), and entangled-photon-pair emitters. The polariton express is gathering speed.
This work has been supported by the NSF and the Engineering and Physical Sciences Research Council.
References
1. A. Griffin, Excitations in a Bose-Condensed Liquid, Cambridge U. Press, Cambridge, UK (1993), p. 1.
2. L. Pitaevskii, S. Stringari, Bose–Einstein Condensation, Oxford U. Press, New York (2003), p. 1
3. A. J. Leggett, Quantum Liquids: Bose Condensation and Cooper Pairing in Condensed-Matter Systems, Oxford U. Press, New York (2006).
4. See, for example, D. W. Snoke, Solid State Physics: Essential Concepts, Addison-Wesley, San Francisco (2009), sec. 11.1.3;
see also M. Combescot, D. W. Snoke, Phys. Rev. B 78, 144303 (2008). https://doi.org/10.1103/PhysRevB.78.1443035. J. Kasprzak, et al., Nature 443, 409 (2006). https://doi.org/10.1038/nature05131
6. R. Balili, et al., Science 316, 1007 (2007). https://doi.org/10.1126/science.1140990
7. K. G. Lagoudakis, et al., Science 326, 974 (2009); https://doi.org/10.1126/science.1177980
Y. G. Rubo, Phys. Rev. Lett. 99, 106401 (2007). https://doi.org/10.1103/PhysRevLett.99.106401
For a review, see M. Richard, et al., Int. J. Nanotech. 7, 668 (2010). https://doi.org/10.1504/IJNT.2010.0317388. J. J. Baumberg, et al., Phys. Rev. Lett. 101, 136409 (2008). https://doi.org/10.1103/PhysRevLett.101.136409
9. A. P. D. Love, et al., Phys. Rev. Lett. 101, 067404 (2008). https://doi.org/10.1103/PhysRevLett.101.067404
10. A. Baas, et al., Phys. Rev. Lett. 100, 170401 (2008). https://doi.org/10.1103/PhysRevLett.100.170401
11. A. Amo, et al., Nature 457, 291 (2009). https://doi.org/10.1038/nature07640
12. A. Kavokin et al., Microcavities, Oxford U. Press, New York, (2007).
13. For reviews of basic polariton condensate theory, see J. Keeling, et al., Semicond. Sci. Technol. 22, R1 (2007);
M. Wouters, I. Carusotto, Phys. Rev. Lett. 99, 140402 (2007). https://doi.org/10.1103/PhysRevLett.99.14040214. D. Bajoni, et al., Phys. Rev. Lett. 100, 047401 (2008). https://doi.org/10.1103/PhysRevLett.100.047401
15. R. Balili, et al., Phys. Rev. B 79, 075319 (2009). https://doi.org/10.1103/PhysRevB.79.075319
16. D. Ballarini, et al., Phys. Rev. Lett. 102, 056402 (2009). https://doi.org/10.1103/PhysRevLett.102.056402
17. S. Utsunomiya, et al., Nat. Phys. 4, 700 (2008). https://doi.org/10.1103/PhysRevLett.102.056402
18. D. Snoke, Nature 443, 403 (2006). https://doi.org/10.1038/443403a
More about the Authors
David Snoke is a professor in the department of physics and astronomy at the University of Pittsburgh in Pennsylvania. Peter Littlewood is a professor in the department of physics at the University of Cambridge in the UK.
David Snoke. 1 University of Pittsburgh, Pennsylvania, US .
Peter Littlewood. 2 University of Cambridge, UK .
