Patterned nanomagnets

A magnet has two poles, as any child can tell you. However, the familiar dipole configuration is not the only one that a magnet can have. The configuration of any magnet is the result of several competing energies: the exchange energy of interaction among the atomic moments, the magnetostatic energy of the magnetic field itself, and the magnetocrystalline anisotropy energy. The relative importance of each of the three energies depends on the size, shape, and material properties of the magnet.

The exchange interaction is what causes magnetic ordering in the first place. The most common representation of exchange energy is the Heisenberg interaction of $-\sum J_{ij\hspace{0.17em}}{\text{S}}_i\cdot {\text{S}}_j$ , a sum of interactions with strength J_ij between neighboring moments S on sites i and j. The minus sign ensures that when J_ij > 0, the lowest exchange energy is found in the ferromagnetically ordered state, in which all the moments are aligned in the same direction. The magnetostatic energy is associated with the magnetic fields generated by any magnetized object and is proportional to the squared field integrated over all space. The Heisenberg exchange interaction does not harbor anisotropy, whereas real magnetic materials have sizable magnetocrystalline anisotropy, so their energy depends strongly on the direction of the aligned moments. In so-called hard magnetic materials, such as magnetite and high-carbon steel, the strong magnetocrystalline anisotropy energy overwhelms the other energies. In contrast, this article focuses on soft magnetic materials, such as nickel, cobalt, and nickel–iron alloys known as permalloy, in which the magnetocrystalline anisotropy is much weaker and the interplay between the exchange energy and the magnetostatic energy leads to a greater variety of configurations.

One of the best venues to explore the range of possible configurations is in patterned nanomagnets with well-defined shapes in the submicron size range. ¹ The exchange and magnetostatic energies in that regime are of similar magnitude, so small variations in size and shape can shift the energy balance between the exchange energy, which favors parallel alignment of the magnetic moments, and the magnetostatic energy, which promotes magnetic closure structures with no stray magnetic field. (For simplicity, we assume the magnetocrystalline anisotropy energy to be negligible.) Many of the resulting configurations are unseen in either soft or hard macroscopic magnets. Patterned nanomagnets are central to many magnetic technologies, such as magnetic recording read heads ² already in use and magnetoresistive random access memory (MRAM) ³ still being developed. In such applications the proper choices of size and shape of the nanomagnets are essential in capturing the unique magnetoelectronic properties.

The studies of the spin configurations and the intriguing phenomena in nanomagnets require advanced fabrication, imaging, and measurement techniques together with theoretical understanding and micromagnetic simulations. Many revealing results have only become available during the past few years. In this article we concentrate mainly on circular nanomagnets, but nanomagnets can have various shapes, including spheres, wires, tubes, disks, and rings. Fabrication methods must produce nanomagnets with well-defined shapes and sizes and with smooth sidewalls. The magnetic configurations can be imaged by spin-sensitive microscopies, such as magnetic force microscopy (MFM) and x-ray microscopy.

Single-domain state

The exchange energy is minimized when all the moments are aligned to form the single-domain state, shown in figure 1a, with a saturation magnetization M _S and a dipole moment of µ = M _S V, where V is the volume of the nanomagnet. Any deviation from parallel alignment increases the exchange energy with an energy density proportional to both the strength of the exchange interaction and the square of the magnetization gradient. Other important lengths are l _ex, the length scale of the exchange interaction, and δ _w, the domain-wall width. For most soft magnets, l _ex is a few nanometers and δ _w is a few times l _ex. In flat nanomagnets with a thickness of about l _ex, there is little magnetic variation within the thickness. The magnetic configuration at the surface is the same as the configuration within the disk.

For very small nanomagnets with dimensions of a few tens of nanometers, the exchange energy dominates and the single-domain state is energetically preferred. In larger nanomagnets, the single-domain state is replaced by other configurations dependent on the shape of the magnet. For circular disks, the single-domain state is succeeded by the vortex state.

Vortex state

Consider a thin circular disk of diameter D and with thickness t much less than D. The magnetostatic energy of the single-domain state increases with the disk dimensions. In the vortex state, shown in figure 1b, the moments in a circular disk are arranged in closed loops. The vortex structure has no pole, no net magnetization, and no stray field, but with a cost in the exchange energy. Because the exchange energy density decreases with the distance from the center, the exchange energy of the vortex state has a weaker dependence on D than does the magnetostatic energy of the single-domain state. Consequently, a sufficiently large disk acquires the vortex state. ⁴ For permalloy disks 15 nm thick, the crossover occurs at a diameter of about 100 nm. The chirality of the vortex structure can be either counterclockwise or clockwise.

The otherwise perfect vortex arrangement is altered because of the large exchange energy density near the singularity at the vortex center. It is energetically favorable for the magnetic moments within a small central region, called the vortex core, to revolt and align perpendicular to the disk plane, as shown in figure 1c. Spin-polarized scanning tunneling microscopy reveals that the vortex core size is approximately the exchange length. ⁵ The polarity of the core can be either up (p = +1) or down (p = −1). The vortex is therefore a three-dimensional spin structure with four possible combinations of chirality and core polarity. Vortex cores also appear in other contexts, most notably the normal cores in the vortices in superconductors and superfluids, but those vortices lack the two possible core polarities available to magnetic vortices.

Square disks of similar size also adopt a vortex state, shown in figure 1d, known as the Landau structure. The configuration consists of four triangular domains with aligned moments, in contrast to the continuously varying magnetization of the moments in a circular disk. The four domain walls intersect at the vortex core in the center of the disk.

Vortex structures have been observed by several different techniques, such as MFM, ⁶ photoemission electron microscopy, ⁷ and electron holography. Most of the techniques have either vertical or in-plane contrast but not both: MFM can detect the polarity of the vortex core but not the chirality of the vortex, whereas PEEM can detect the chirality of the vortex but not the polarity of the core. The various techniques reveal the intricate physics of the vortex state over the limited size range in which it exists.

Vortex dynamics

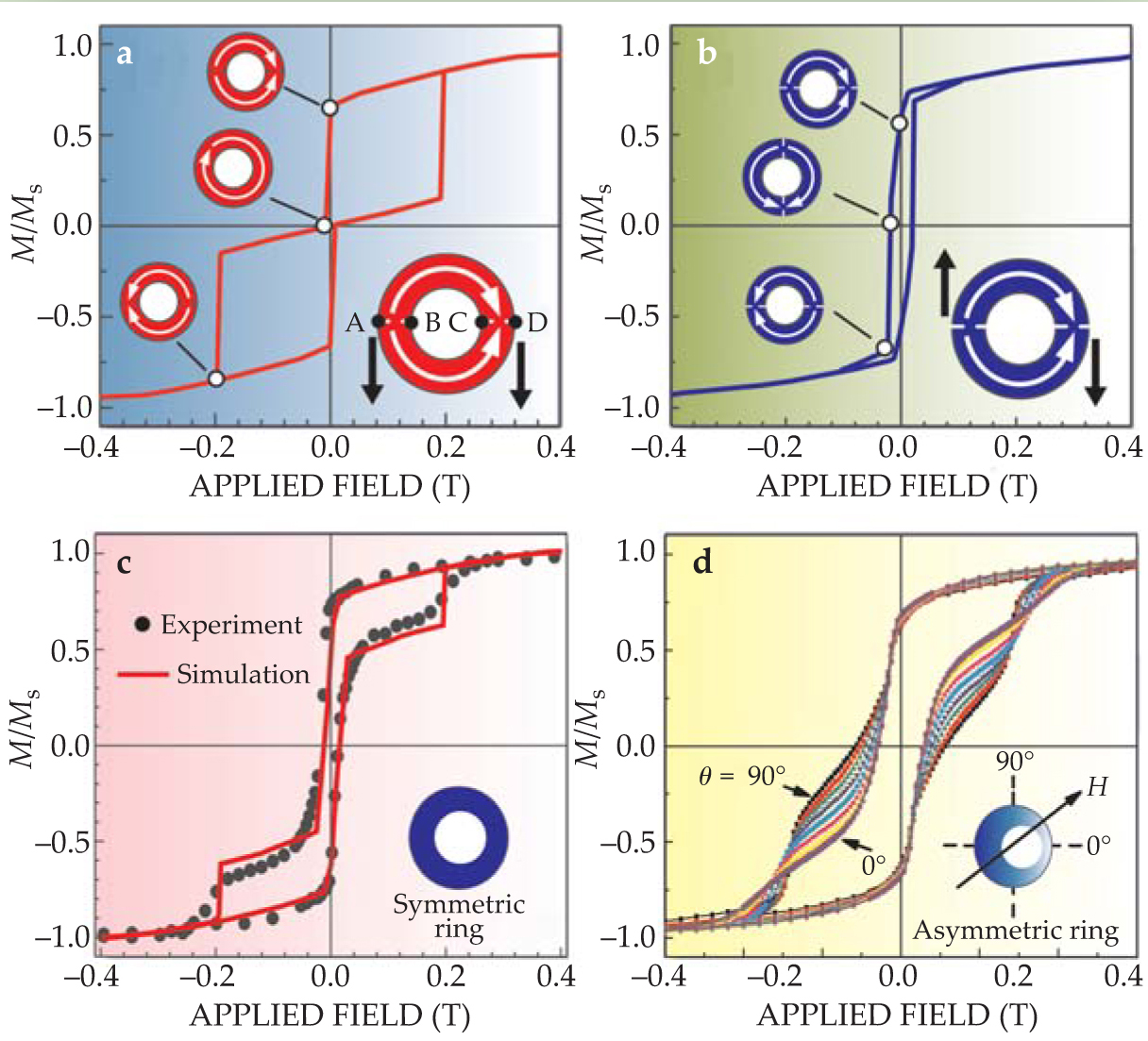
Figure 2 depicts the response of circular magnets to an applied magnetic field. At zero field, a 200-nm permalloy disk is in the vortex state, and the in-plane magnetization is zero. When a small magnetic field is applied, the portion of the vortex with spins parallel to the field expands, and the vortex moves perpendicular to the field. A counterclockwise vortex moves to the left as viewed in the direction of the field, and a clockwise vortex moves to the right. There is a concomitant increase in magnetization linearly dependent on the applied field H. The movement of the vortex continues until the vortex core reaches the edge of the disk and disappears at the annihilation field H _A, at which M abruptly increases. A slightly larger field beyond H _A aligns the disk into the single-domain state. When the applied field is then reduced, the core does not reappear until H reaches the nucleation field H _N, at which point the magnetization drastically decreases. The new vortex may or may not have the same chirality as the original vortex. The values of H _N and H _A depend strongly on the size, thickness, material, and defect density of the disk; a representative range for H _A is 0.05–0.3 T. The nucleation field H _N can even be negative for small disks, as shown by the red curve in figure 2.

Within the field range −H _A < H < +H _A, the motion of the vortex core is reversible. The changing magnetostatic energy provides a restoring force, analogous to that of a Hooke’s-law spring, that pulls the vortex core back toward the center of the disk. The initial susceptibility, M/H, provides a measure of the stiffness of the sideways movement of the core. If the vortex core is rigid, its displacement is proportional to H. ⁸

The direction of the vortex core’s motion under a DC magnetic field reveals only the chirality of the vortex, not the polarity of the core. However, in response to an AC magnetic field of small amplitude, the vortex core not only oscillates but also executes a circular motion known as gyration. The gyrovector G of the vortex core is defined as −(2π ptM _S/γ)z, where p is the polarity of the vortex core, t is the thickness, M _S is the saturation magnetization, γ is the gyromagnetic ratio, and z is the unit vector perpendicular to the disk. The gyrotropic force on the vortex core is G × v, where v is the velocity of the vortex core. Because the effective mass of the vortex core is small, the core’s trajectory is determined by the balance of the gyrotropic force and the magnetostatic restoring force described previously. ⁹

The direction of the gyrotropic force with respect to the velocity is independent of the vortex chirality and depends only on the core polarity or, more formally, on the topological invariant known as the skyrmion number, which is + $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ for an up core and − $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ for a down core, ¹⁰ as shown in the box below. Consequently, the direction of gyration reveals the polarity of the vortex. A down vortex core gyrates clockwise, and an up vortex core gyrates counterclockwise. One can also apply a field pulse and observe the decay of the spiraling motion of the vortex core, whose trajectory likewise reflects the polarity. ⁷ The resonance frequency of the gyration depends on the relative magnitudes of the restoring force and the gyrotropic force and is in the 100-MHz range for permalloy disks 20 nm thick and 2 µm in diameter. Measuring the vortex gyration therefore requires a microscopic imaging technique with a time resolution of nanoseconds. Suitable techniques have recently become available, ⁷ so it is possible to measure both the vortex chirality and the core polarity via the dynamics of the vortex in response to an applied field.

Reversing the vortex core’s polarity by applying a magnetic field perpendicular to the disk requires a large field of about 0.3 T. Bartel Van Waeyenberge and colleagues ¹¹ recently demonstrated that the core polarity can also be reversed by a pulsed in-plane field of only 1.5 mT, a useful technique that facilitates the use of the vortex core to store information. The process involves the creation of a new vortex–antivortex pair with like polarities opposite to the original vortex. The subsequent annihilation of the old vortex and the antivortex changes the total skyrmion number, and thus produces a burst of spin waves as described in the box. ^{11 , 12}

Two vortices can be created in an elliptical disk, ¹³ as shown in figure 1e. Because the two vortices share the middle portion, they must be of opposite chirality. However, the polarities of the two cores are independent of the vortex chiralities. The two-vortex system provides a way to study the interaction between vortices. As shown in figure 1f, when a static magnetic field is applied along the long axis of the ellipse, the two cores move in opposite directions along the short axis, which results in two equivalent states with the same microwave resonance frequency. However, if the static field is along the short axis, the two cores shift away from or toward each other depending on whether the central region is magnetized parallel or antiparallel to the field. Because the two vortices share some of the spins in between them, the gyrotropic resonance frequency decreases by as much as 50 MHz when they move toward each other and increases by about the same amount when they move away from each other. The resonance frequency also depends on the relative core polarities. In general, when the field is along the long axis of the ellipse, vortices of the same polarity have a higher resonance frequency than vortices of opposite polarity. When the field is along the short axis, vortices of opposite polarity have a higher resonance frequency.

Nanorings

The topological difference between a nanoring and a circular disk is reflected in the differences in their properties. The vortex core, which has such influence over the dynamics of a circular disk, is absent in a nanoring, as long as the ring width is less than the domain-wall width of about 50 nm. Most nanorings reported to date, with diameters between 0.5 and 5 µm, have been made by electron-beam lithography. ¹⁴ Template lithography, shown in figure 3, allows the fabrication of smaller nanorings with diameters of 100 nm and ring widths of 20 nm. ¹⁵

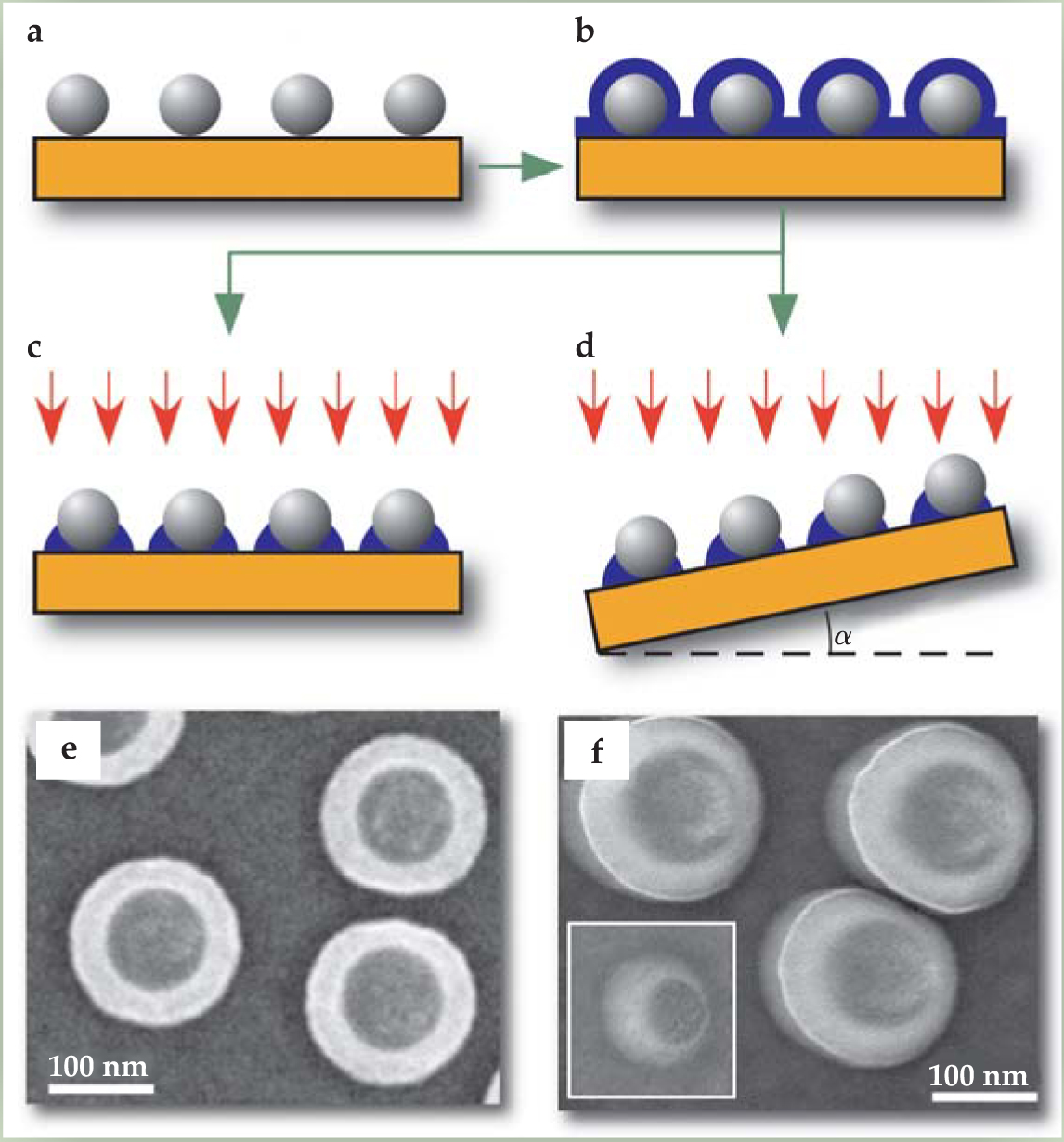
In the first step in template lithography, monodisperse nanospheres, such as 100-nm polystyrene spheres, are attached to a substrate by chemical means. A metal film is then deposited over the entire surface, including the regions below the nanospheres. An argon-ion beam at normal incidence etches away all materials except those protected under the spheres. The resulting nanorings have tapered cross sections. The diameter and number density of the nanospheres determine those of the nanorings. The thickness of the nanorings, measured perpendicular to the plane, can be as much as the radius of the nanospheres.

In the remanent state at zero field (after being magnetized with a large magnetic field), a nanoring acquires the so-called onion state, shown in figure 4, in which two semicircular domains are separated by two domain walls 180° apart. The two domain walls can also be viewed as two poles. When a magnetic field is applied opposite to the nanoring’s magnetization, the two domain walls move, with two possible routes. In the vortex process, shown in figure 4a, the two domain walls move toward each other along one segment of the ring. Only a small field is required to annihilate the domain walls and form the vortex state. A much larger field is needed to re-create from the vortex state two new domain walls, which then move in opposite directions until achieving the oppositely oriented onion state.

Alternatively, in the onion-rotation process, the two domain walls move in tandem and maintain their 180° separation, as shown in figure 4b. The vortex state and the onion state in a nanoring, in which the magnetostatic energy and the exchange energy dominate, respectively, are reminiscent of the vortex state and the single-domain state in a circular disk. Indeed, in nanorings of larger diameter, switching of the magnetization orientation via the vortex process is favored, whereas the onion-rotation process prevails in smaller-diameter rings. In nanorings 100 nm in diameter, the two processes have similar probability. When an array of 100-nm nanorings is switched, the observed behavior, shown in figure 4c, is the superposition of the two processes weighted by their probabilities, which have been determined to be 40% and 60% for the vortex process and onion-rotation process, respectively.

The vortex state of a nanoring also has two chiralities. In symmetric nanorings, which have a uniform cross section along the circumference, both vortex chiralities are equally likely to be formed during the vortex process. The switching behavior of the symmetric nanorings is isotropic, independent of the direction of the in-plane magnetic field. Theory and simulations have suggested that a domain wall tends to move toward a region of reduced cross section. That tendency has been observed in asymmetric nanorings, in which one side is wider and thicker than the other. The asymmetric nanorings are made by the same template fabrication process, but with the argon-ion beam incident at an oblique angle, as shown in figure 3d.

Asymmetric rings have in-plane anisotropy. Their switching behavior depends on the direction θ of the initial magnetic field. Within the plane of the rings, the symmetry axis is defined such that the thinnest point of the ring is at θ = 0° and the thickest is at θ = 180°. For rings approximately 100 nm in diameter, the fraction of rings that undergo the vortex process increases from 40% at θ = 0° to essentially 100% at θ = 90°, at which point the two domain walls in the onion state nearly always move toward the side of the ring with the smaller cross section. ¹⁶ Representative hysteresis loops are shown in figure 4d. Furthermore, if the magnetic field is first applied along θ = 90°, upon reversing the field all the nanorings acquire the vortex state with the clockwise chirality, whereas at θ = −90°, they acquire the counterclockwise chirality. Hence, not only can all asymmetrical nanorings be made to form the vortex state, even their chirality can be controlled.

In the vortex process, the vortex is created by the annihilation of two domain walls. That annihilation is possible only if the nanoring is sufficiently thick. Each of the two domain walls can be treated as a combination of two half vortices: ¹² one on the outer edge of the ring with winding number − $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ and one on the inner edge with winding number + $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ . The half-vortices with the same winding number cannot annihilate in arbitrarily thin nanorings. When the thickness of the ring is above about 10 nm, the vortex process ending with the true vortex state, as shown in figure 4(a), can take place. However, for thinner nanorings, the two domain walls can approach each other but cannot annihilate. The result is a less-than-ideal magnetic configuration, known as the twisted state, that can be exploited as described below.

Applications

Nanomagnets feature prominently in a number of applications, including read heads ² and MRAM. ³ The nanomagnets in those devices must perform reliably and controllably in response to magnetic fields and electric currents. Circular-disk magnets have mostly been avoided because of the various configurations they can adopt. Instead, most applications use nanomagnets of an oblong shape in which the magnetostatic energy causes the magnetic moments to align along the long axis to create two definite orientations. The unique attributes of nanorings offer new prospects.

Whereas a read head is a single device, MRAM is an array of a large number of memory units, each of which must be individually addressed and accessed. The giant magnetoresistive (GMR) effect and, more recently, the tunneling magnetoresistive effect enable direct electronic readout from multilayer nanomagnet structures. ¹⁷ The multilayer contains two magnetic layers: the storage layer, which can be switched between two definite magnetic states, and the reference layer, which is kept in one particular state. Separating the storage and reference layers in GMR devices is a thin metallic layer; in magnetic tunnel junctions, the intervening layer is an insulator that acts as a barrier for spin-dependent quantum tunneling between the two magnetic layers. MTJs are appealing because they have a higher impedance than GMR devices; what is more important, they have an extremely high magnetoresistance ratio, defined as the percent difference in the resistance between the states in which the magnetizations of the two magnetic layers are parallel and antiparallel to each other. Magnetoresistance ratios of more than 400% at room temperature have been observed in MTJs that use crystalline magnesium oxide as a tunnel barrier between cobalt- or iron-based magnetic layers, with the crystalline structures of the layers epitaxially matched at the interfaces. ¹⁸

The first generation of MRAM, now commercially available with a capacity of 4 Mbits, employs two large currents to generate the necessary magnetic fields for switching a specific MTJ. That scheme of switching from a distance is not scalable, because for very small MTJs the switching field spills over into neighboring cells, so the prospects for using the scheme in high-density memories are limited. However, the high spin polarization in the MgO-based MTJs is well suited for spin-torque-driven switching, in which the magnetization is switched by passing a current of spin-polarized electrons through the MTJ. That switching scheme can more readily target the desired MTJ with no effect on its neighbors, and the required amplitude of the switching current is small when the size of the MTJ is in the range of 100 nm.

The dependence of magnetic-switching behavior on the shape of a nanomagnet may hold the key to the miniaturization of MRAM. In the oblong memory elements currently in use, any geometric, morphological, or physical variations of the tapered ends and along the edges of the elements can cause significant changes in the switching-field threshold. An alternative is to use ring-shaped memory elements, shown in figure 5a. The nanoring geometry not only eliminates sharp ends but also requires a much smaller switching current.

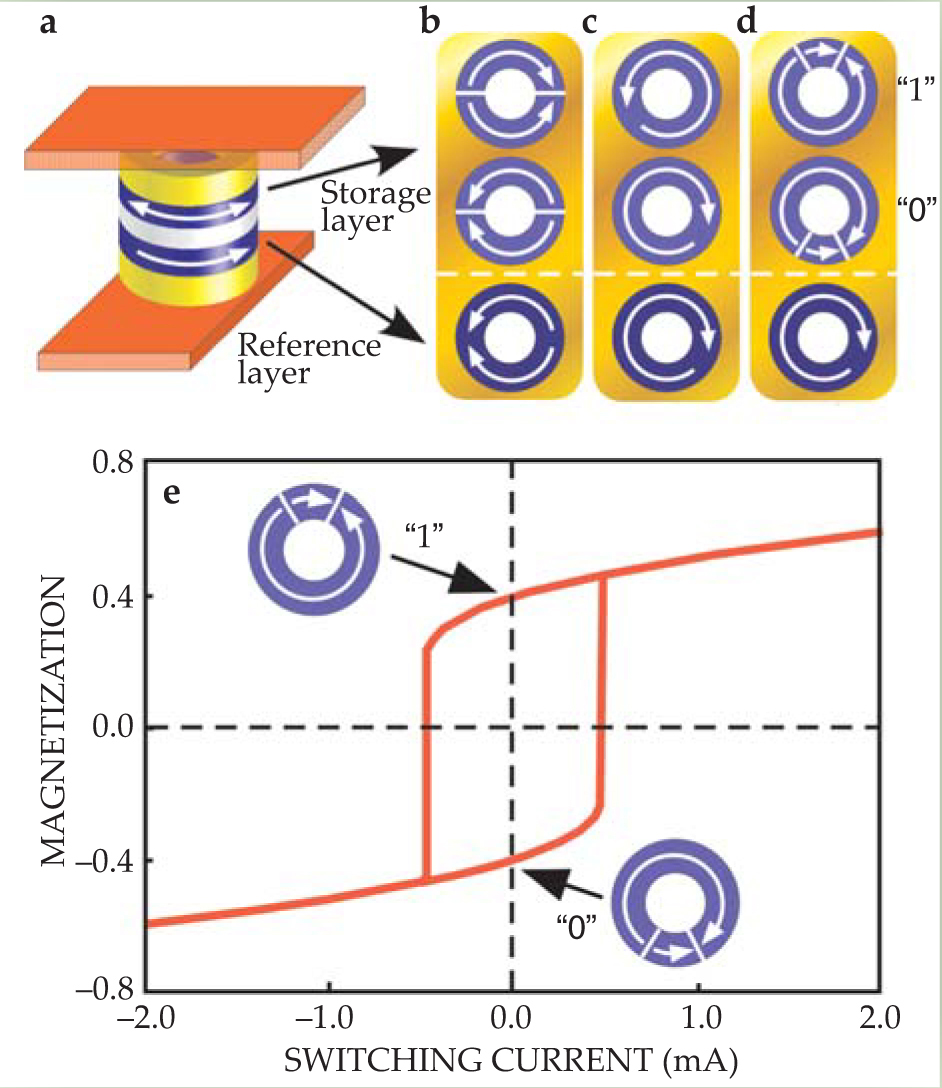
Several schemes for nanoring MTJs have been proposed. In the first scheme, the reference layer and the storage layer are both in the onion state. The two orientations of the onion state shown in figure 5b provide the two memory states in the storage layer. The scheme is similar to the dipole-based scheme already in use, except that the switching current for the ring element in the onion state is significantly less than that for a disk. In the second scheme, both the reference layer and the storage layer are in the vortex state, and the two different chiralities in the storage layer provide the memory states, as shown in figure 5c. Although such a scheme might be aesthetically more pleasing, a high switching current is required to reverse the chirality of a vortex.

A more advantageous scheme, shown in figure 5d, uses the vortex state in the reference layer and the twisted state in the storage layer. Those states can be achieved if the reference layer is more than 10 nm thick and the storage layer is less than 10 nm thick. The spatial proximity of the domain walls in the twisted state leaves the rest of the ring magnetized with a single chirality. The chirality of the ring can be reversed by a perpendicular current that moves the domain walls away from each other so that they meet at the opposite side of the ring. Micromagnetic simulation results, shown in figure 5e, indicate robust and repeatable switching, with a very low switching current, between the two well-defined memory states. The switching from one chirality to the other is accomplished by a combination of the current-generated Amperean field and the spin torque that arises from the spin polarization of the current. Several groups are currently exploring schemes for nanoring MTJs.

The rich and fascinating phenomena exhibited by nanomagnets depend intricately on the magnets’ shape and size. The engineering of patterned nanomagnets with well-defined memory states and robust, repeatable, and uniform magnetic switching characteristics is a fertile area for exploring future magnetic and magnetoelectronic devices. As vividly displayed by the examples above, although the dipole configuration is a familiar and useful state that a magnet can acquire, it is certainly not the most interesting one.