Optical Studies of Single Quantum Dots

Atomic physics progressed rapidly at the beginning of the last century, thanks, in large part, to optical spectroscopy. Quantization and spin were discovered through optical studies, as were other fundamental atomic properties. With the advent of the laser, physicists learned how to manipulate atomic wavefunctions by applying coherent optical fields. More discoveries followed. Now, at the beginning of the new century, optical techniques are being used to explore a new scientific frontier: the atomlike entities known as quantum dots (QDs).

Measuring 1–100 nm across, QDs are semiconductor structures in which the electron wavefunction is confined in all three dimensions by the potential energy barriers that form the QD’s boundaries. ¹ A QD’s electronic response, like that of a single atom, is manifest in its discrete energy spectrum, which appears when electron–hole pairs are excited. Although the wavefunction of a QD electron, and its corresponding hole, extends over many thousands of lattice atoms, the pair—termed an exciton—behaves in a quantized and coherent fashion.

The coherence is relatively easy to detect and control optically—for two reasons. First, the superposition of the ground and excited states dephases more slowly in QDs than in higher-dimensional semiconductor structures. Second, QDs have large dipole moments (50–100 times larger than those of atoms). Thanks to these advantages, it is possible to probe and manipulate the wavefunction of a single QD. ²

QDs possess another attractive property. Their size, shape, and composition can all be tailored to create a variety of desired properties. These “artificial atoms” can, in turn, be positioned and assembled into complexes that serve as new materials. We and others who work on QDs anticipate that a host of complex, customized QD-based materials will become available.

Many types of QD materials have already been developed. Among them are QDs formed by electrostatic gates. Researchers study these QDs with far-infrared spectroscopy and with transport techniques, such as conductance measurements. Great advances have been made with electrostatic QDs, but this type of QD does not interact strongly with light because the electrostatic gates separate the electrons and holes, severely reducing the QD’s dipole moment.

Fortunately, some types of QDs do interact strongly with light and are being studied in detail, even at the single QD level. Grown as part of a larger crystalline structure, epitaxial QDs form spontaneously in molecular beam epitaxy (see the article by Pierre Petroff, Axel Lorke, and Atac Imamoglu, Physics Today, May 2001, page 46 ). Epitaxial QDs are especially attractive to researchers because they lack the defects caused by etching, regrowth, and other processing steps. Another advantage of epitaxial QDs is that they lie far beneath the surface of the surrounding material whose associated states are potentially meddlesome. Colloidal chemistry provides yet another way of growing QDs. ³ The various types of QDs each have their advantages and disadvantages and all have served as useful models in research aimed at gaining a better understanding of the optical properties of QDs.

All QD arrays have distributions in size, shape, and so on that lead to inhomogeneous spectral linewidths and blurry data. To avoid this problem, many researchers use extremely high spatial resolution to probe the optical spectra of single QDs (see figure 1). Optical studies of single QDs reveal how similar QDs are to atoms and have led to two general, and quite different, breakthroughs.

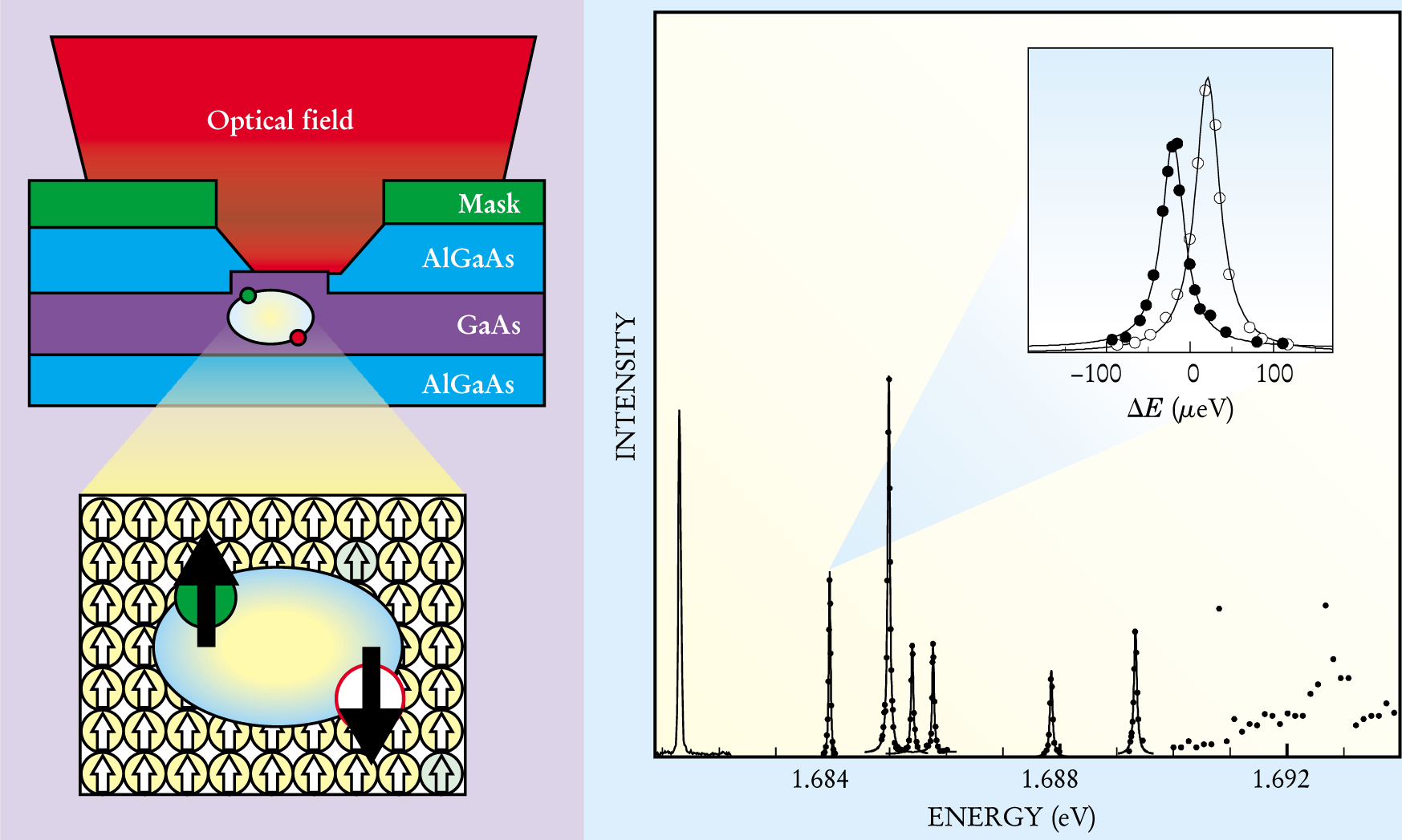
First, working with single QDs rather than QD arrays boosts spectral resolution by a factor equal to the ratio of the inhomogeneous linewidth (10–100 meV) to the homogeneous linewidth (1–100 μeV). As a result of that enormous improvement, QD researchers have made a flurry of new and direct observations of fine-structure splittings, hyperfine shifts, and so on. Just as in the case of atoms, these splittings contain the details of spin interactions and other subtle quantum mechanical properties. Second, working with single QDs dispenses with the complexities of ensemble averaging. Consequently, it is possible to control the full quantum mechanical wavefunction of a QD. The new and exciting opportunities opened up by these breakthroughs form the subject of this article.

Optical excitations

In the neutral ground state of an undoped and unexcited QD, all the single-particle valence states are filled with electrons, while all the conduction states are empty (see the lower right hand corner of figure 2(a)). When light excites an electron across the bandgap, the electron leaves behind a hole. Together, the electron and hole form an exciton. The lowest-energy orbital state of an exciton comprises four substates that correspond to the four doubly degenerate electron and hole states. (Here we focus for clarity on the disklike QDs typical of epitaxial systems. Details differ for other QD types, such as the nearly spherical colloidal QDs.)

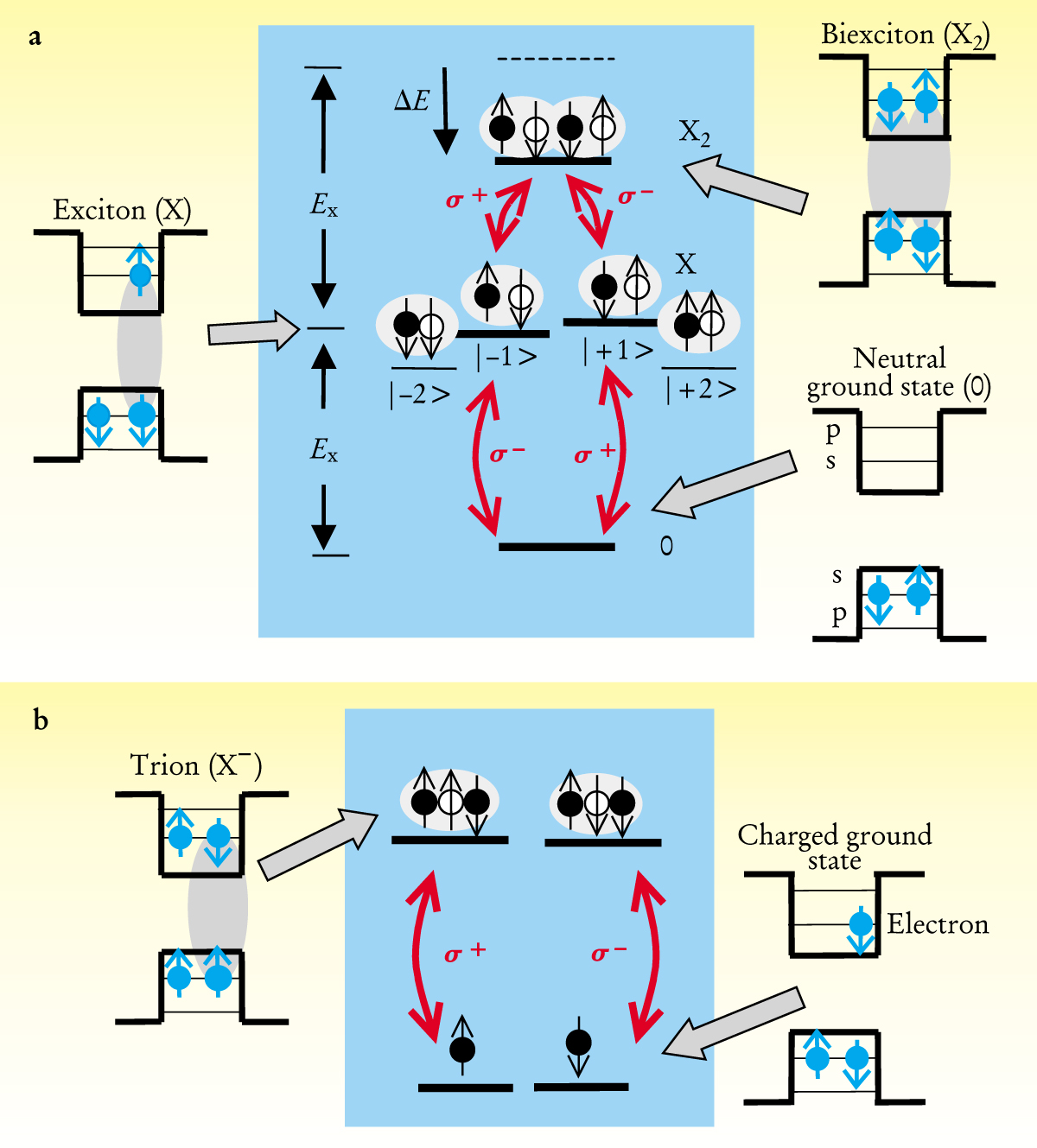
Two of the tour substates can be optically excited, whereas the other two (termed dark states) are normally forbidden by quantum selection rules. Often, the two dark states can be ignored. For example, we and our collaborators have used optical pulses to create quantum beating between the two bright substates and the QD ground state. The dark states do not participate in the beating. ²

The substates’ spectral lines have fine-structure splittings caused by spin interactions, such as the exchange Coulomb interaction, hyperfine interactions with the underlying nuclear spin, and the Zeeman interaction with an applied magnetic field. Though small, these spin interactions can be resolved in the spectrum of a single QD, as shown in figure 1.

With sufficient power, a laser tuned above the bandgap can create a second exciton within the same QD. This two-exciton state is called a biexciton (see figure 2(a)). Its lowest-energy state is a singlet in which both electrons and both holes occupy the lowest-energy orbital state. Because of Coulomb interactions between the two excitons, it takes a little less energy to create the second exciton than to create the first. Consequently, if the QD is in a biexciton state, it can emit two photons of different frequency. The first photon originates in the transition from the biexciton to the exciton state; the second, more energetic photon originates from the transition from the exciton to the neutral ground state.

This interaction energy between excitons leads to the possibility of generating single photons on demand. A strong laser pulse can create a state of many excitons, each of which has a different energy. But only one photon is emitted at the single exciton transition energy. A narrow bandpass filter tuned to the single exciton emission line can therefore be used to realize a solid-state source of single photons. A QD may also emit single pairs of correlated photons or even pairs of entangled photons.

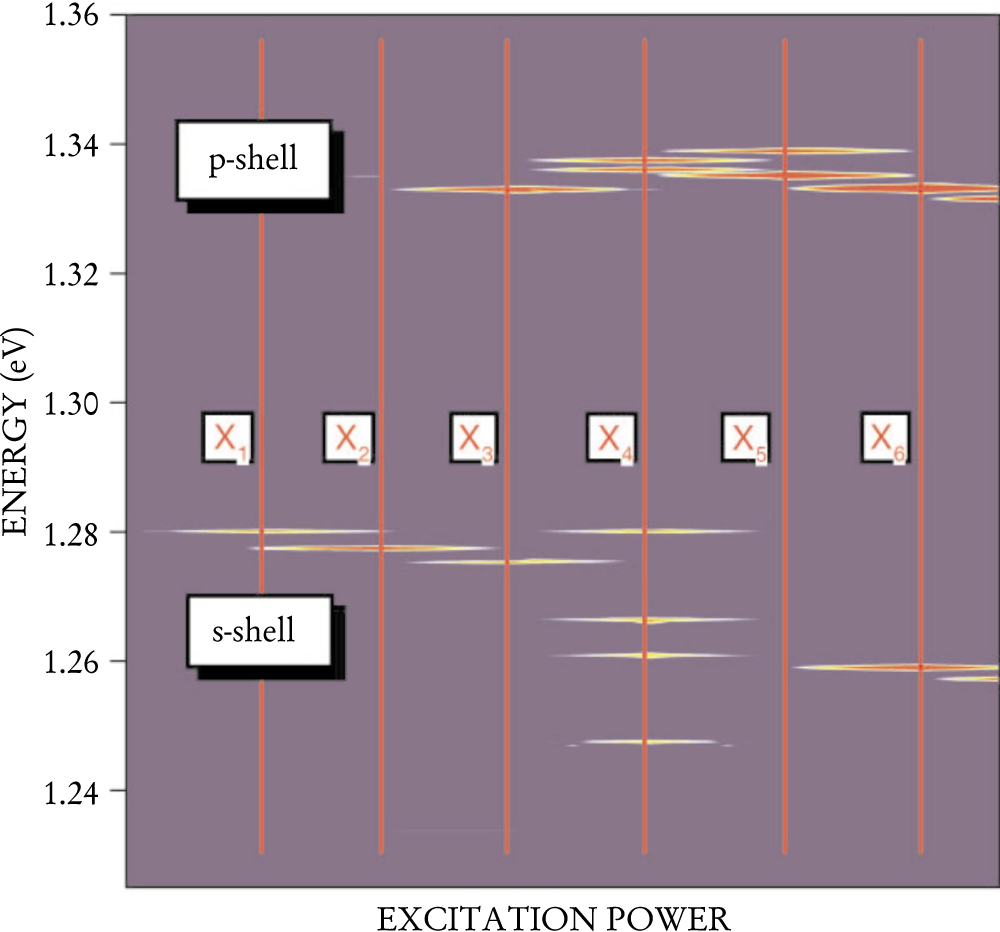
It is also possible to put three or more excitons into a single QD. Because of the exclusion principle, the third exciton must go into the next excited orbital state. Beautiful examples of multi-exciton states have been observed in self-assembled indium arsenide/gallium arsenide QDs. Manfred Bayer of the University of Würzburg in Germany and his collaborators have measured the properties of QDs that contain up to six excitons (see figure 3). ⁴

If an electron is injected or doped into a QD, the QD’s spin structure changes. The ground state of a QD charged with a single electron has spin- $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ and is doubly degenerate. Such a QD can be optically excited into a state that consists of a negatively charged exciton with two electrons and a hole (the negative trion; see figure 2(b)). Thanks to selection rules, an experimenter can probe the spin states of both the electron and the trion. For example, a circularly polarized photon will either excite the QD or not, depending on whether the electron is spinning up or down. Potentially, this phenomenon could form the basis of a highly sensitive probe of single electron spin.

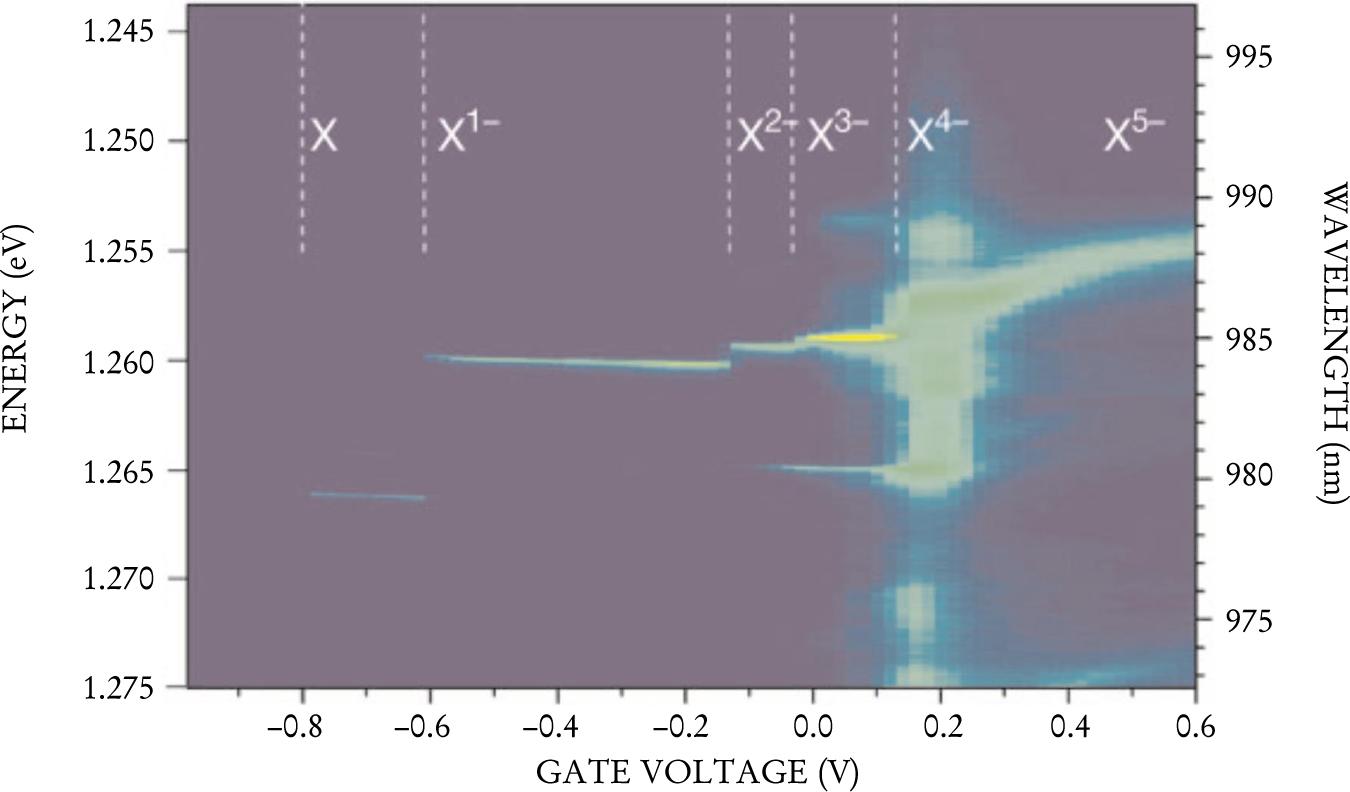
One can inject a QD with two, three, or more additional electrons while continuing to probe the QD through the exciton’s optical spectrum (see figure 4). Holes can be injected too, as David Regelman of the Technion–Israel Institute of Technology in Haifa and his collaborators have recently demonstrated. ⁵ Moreover, charged QDs can be injected with multiple excitons. The properties arising from these “designer atoms” are only just beginning to be investigated.

Coherent optical control

Like atoms, QDs can be regarded as pointlike systems. In higher-dimensional systems—such as quantum wires, quantum wells, and bulk systems—the optical excitation of a semiconductor (the exciton) has an energy continuum that arises from the exciton’s freedom to move through the crystal. By contrast, the QD exciton is fully localized. Moreover, it can be restricted to a single state. Such selection is possible because unwanted states can be excluded if they lie outside the bandwidth of the exciting laser or if they are forbidden by the selection rules of optical polarization.

When unwanted states are inaccessible, a QD can be modeled as a two-level system in which an exciton is either present or absent. This simplifying approach was pioneered nearly 50 years ago by Richard Feynman, Frank Vernon, and Robert Helwarth. In a classic paper, they demonstrated that any two-level optical system can be mapped directly into a spin- $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ system described by a Bloch vector. ⁶ If the phase coherence time of the QD is long enough, a strong coherent laser field can rotate the Bloch vector of this artificial two-level atom, driving the QD completely up to the exciton state and back again (a Rabi oscillation). Four groups have recently reached this milestone. ⁷

In the simplest case, Rabi oscillations of frequency ${\Omega }_{\text{R}}=\mu E/\hslash$ can be seen as oscillations in the excitations of the QD as a function of the area of a resonant laser pulse ${\Omega }_{\text{R}}\tau$ , provided the pulse width τ is less than the dephasing time. Here, μ is the dipole moment and E is the optical field amplitude. If the QD is initially in the ground state, the probability of its promotion to the excited state is given by cos² $\left({\Omega }_{\text{R}}\tau /2\right)$ . When ${\Omega }_{\text{R}}\tau =\pi$ (a pi pulse), the system is completely inverted—that is, rotated.

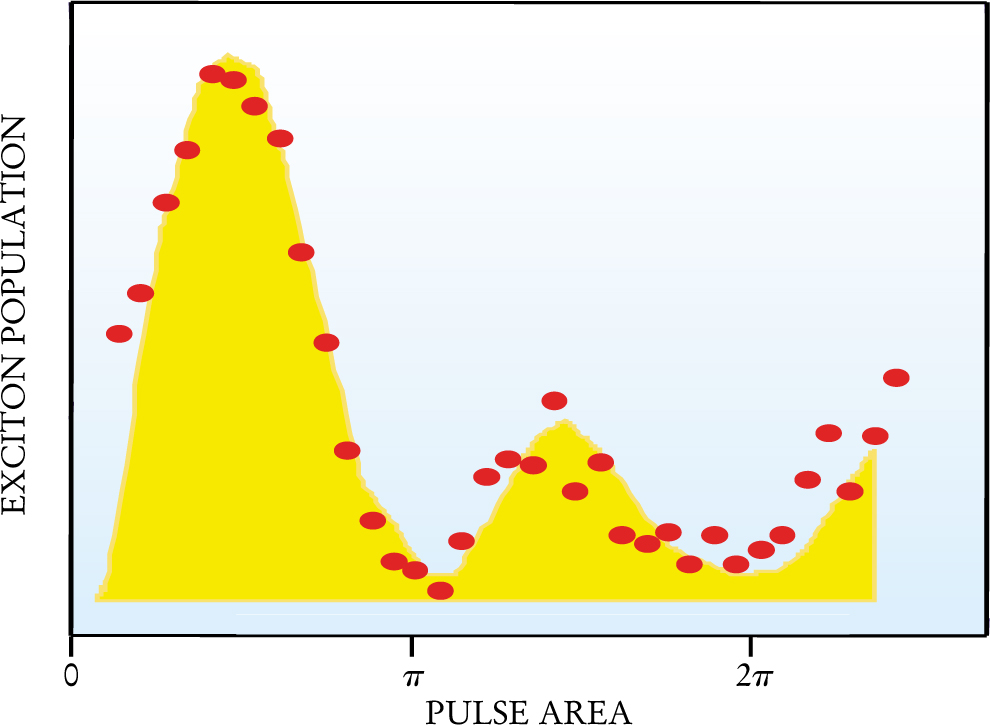
The Rabi oscillations in QDs are much simpler than the Rabi-like oscillations executed by extended-state excitons in higher dimensional structures. Furthermore, the transition moment μ can be much larger in QDs than in atoms. As a result, Rabi oscillations in QDs can be induced at relatively low laser intensities. Figure 5 shows the observed oscillation of a single exciton transition as a function of the pulse area. In this experiment, a pump probe coherently excites the QD. As the pump pulse intensity is increased, the excited state’s population oscillates. These oscillations, known as Rabi flopping, are measured by the change in transmission of a probe pulse arriving at the QD a constant delay time later than the pump pulse.

Of course, the two-level model is just an approximation. In a real system, complications abound. For example, the exciton exists on a lattice of atoms whose vibrations and nuclear spins can interact with the exciton. Moreover, a real sample often contains other weakly bound and fluctuating electrons nearby that may also interact with the QD. And if the biexciton energy shift is not small with respect to the bandwidth of the laser, the two-level approach fails and one or more additional levels must be incorporated into the modeling. Researchers have devoted much effort to understanding the nature and extent of these internal interactions and the resulting relaxation processes. This knowledge forms the foundation for the design of the next generation of QDs.

The basic quantum mechanical nature of a single QD’s optical response may ultimately spawn revolutionary new technologies. Among the most exciting is quantum information technology. Thanks to the long-lived quantum coherence of QD excitons, researchers can control the state of excitation using optical pulses (see the article by David Awschalom and James Kikkawa, Physics Today, June 1999, page 33 ). The strong anharmonicity of the energy levels, the sharp transition energies, the large optical oscillator strengths, and the relatively weak environmental coupling all make QDs potentially valuable for storing quantum phase imparted by a coherent optical field. Because of its ability to preserve phase, the QD system can exist in useful quantum superposition states—a key requirement for realizing the potential of quantum computation.

Using coherent nonlinear optical spectroscopy techniques, arbitrary states of quantum entanglement can be formed within a single dot. The present generation of experiments has been critical in showing that such states can be optically created and detected in a dot system and that they do not lose phase coherence during the measurement. We anticipate that the next generation of experiments will show entanglement between pairs of distinct dots.

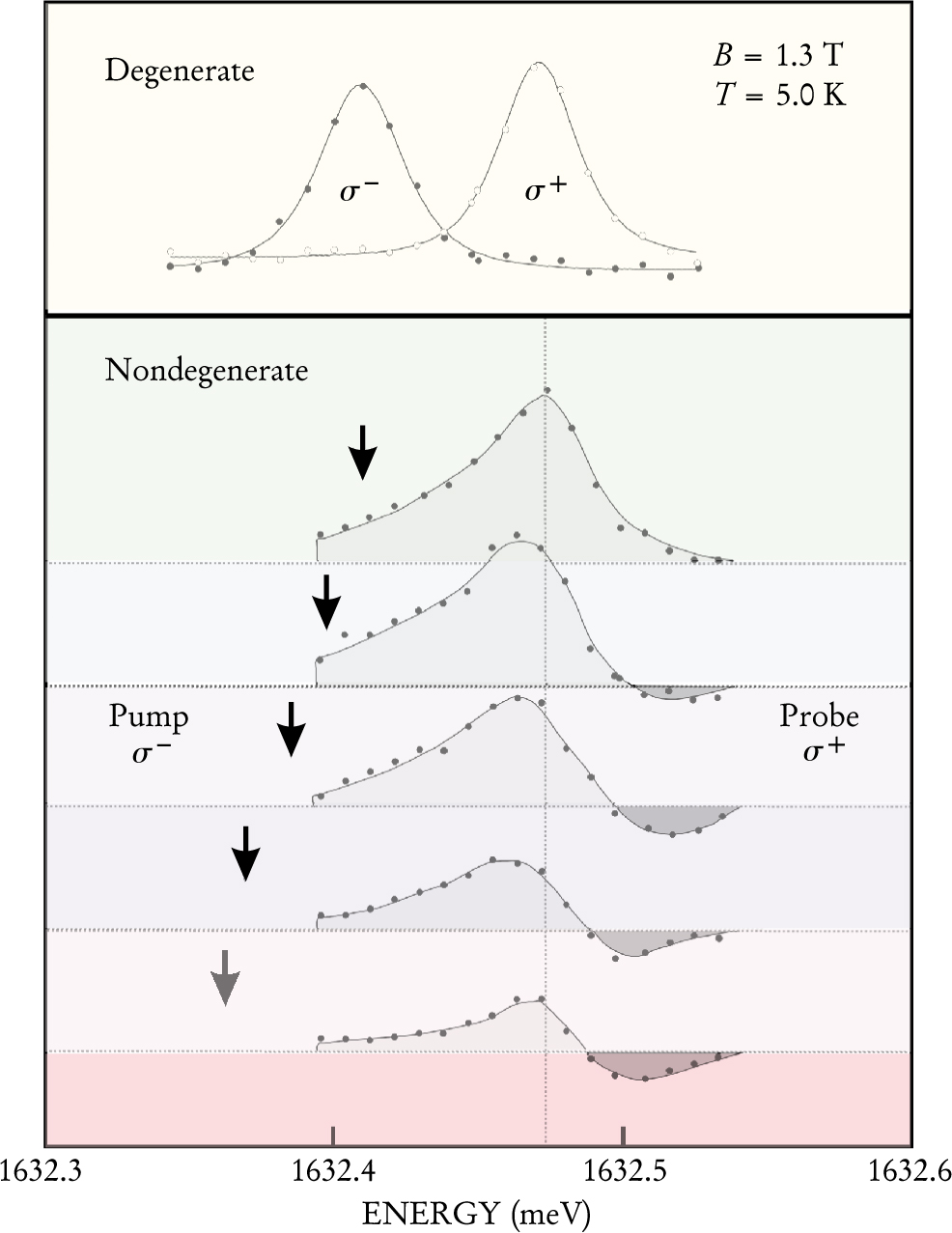
An example of an entangled state involving excitons is shown in figure 6. Creating the wavefunction that corresponds to this picture requires two optical fields of the appropriate energy and polarization and a mutual coherence time longer than that of the entangled state. Obtaining evidence of the entanglement is more challenging. However, the field of coherent nonlinear optical spectroscopy is well developed and the necessary techniques are well established for atomic systems. For the case of entanglement shown in the figure, the spectral lineshape has a distinctive interference shape (the negative part of the signal).

Controlling electronic and nuclear spins

The subject of spin in semiconductor nanostructures is attracting a lot of attention. Spin could provide not only an alternative to charge as the basis for electronics, but also, thanks to long coherence times, a physical incarnation for long-lived qubits. Unfortunately, the weak interactions that lead to the long coherence times also make spin more difficult to control with transport techniques. Fortunately, however, the spin states of a QD, like those of an atom, can be studied relatively easily through optical spectroscopy. Moreover, single QD spectroscopy makes it possible to measure, and even to selectively excite and control, the spin state of a single QD through optical orientation techniques. Eventually, it will become possible to coherently control a single electronic spin optically.

Radiative recombination ultimately limits the duration of a superposition of eigenstates that includes excitons. This limit can cause problems because excitons, thanks to their strong optical coupling, have relatively fast optical recombination rates. Researchers are therefore investigating QD systems in which the ground state contains sublevels that can be optically manipulated through an intermediate excited state transition. Superpositions of ground-state substates with remarkably long coherence times have already been created in atomic systems. QD systems could follow suit.

Working with pure spin states has another advantage. Unlike the orbital part of the electron wavefunction, which interacts strongly through the electron’s charge, the spin part of the electron wavefunction interacts only weakly with its environment, which results in a long relaxation time. Such a system is realized by a QD doped with a single electron (see figure 2(b)).

Despite the weak coupling, it is possible to probe the electronic spin state optically by means of the trion states (figure 2(b)). According to the selection rules, an electron in one spin eigenstate can be resonantly excited to one of the trion states with a polarized photon. Once excited, it will tend to radiatively recombine to the same spin eigenstate. To supply more emitted photons, this cycle can be repeated until either the trion’s hole or the ground state electron flips its spin. A simple, single-spin detection scheme is one possible application.

Much remains to be done in developing an all-optical approach to quantum computing using coherent spins in QDs. One outstanding problem is the effect of nuclear spin on the underlying lattice of atoms that forms the QD. Nuclear spin manifests itself in two ways. First, it exerts an effective magnetic field on the electron spin through the hyperfine interaction. This effective field, whose magnitude is governed by the average nuclear spin polarization, leads to an average hyperfine shift in the fine-structure splitting. By using polarized light to orient the exciton spin, the nuclear polarization can be optically pumped to high values. The hyperfine interaction leads to the gradual polarization of the nuclear spin through the Overhauser effect. This process is rather slow, but the nuclear spin has such a long relaxation time that the pumping process can be very effective. Recently, 70% of the nuclear spins were polarized in a single gallium arsenide QD through optical pumping. ⁸

The second way in which nuclear spin influences electron spin in QD systems is through fluctuations that lead to the electron spin’s relaxation. In III–V QDs, this effect will likely limit the ultimate spin coherence times and lead to an increased demand for quantum error correction. Interestingly, there may be a way to attack even this problem. Guido Burkard and Daniel Loss of the University of Basel in Switzerland and David DiVincenzo of IBM Corp’s T. J. Watson Research Center in Yorktown Heights, New York, have proposed that the role of the nuclear spin reservoir could be minimized by optically pumping the nuclear spin system into a fully polarized state. ⁹

Molecular engineering

One of the goals driving QD research, and nanostructure research in general, is the creation of complex nanomaterials with customized properties. The goal has two prerequisites. Not only must one be able to fabricate individual QDs with the desired number of electrons, energy structure, optical response, and so on, but one must also be able to position the QDs and even couple them to other QDs or structures. Such an ambitious goal will take an extended research effort, but the first promising steps, both theoretical and experimental, have already been taken.

Four years ago, Loss and DiVincenzo proposed that chains of coupled QDs could be used as registers of quantum bits, provided certain two-qubit rotations could be developed. ¹⁰ Coupled QDs require an interaction between the constituent electrons or excitons. Two groups in Germany—one led by Bayer, ¹¹ the other by Werner Wegscheider of the Technical University of Munich ¹² —have observed such interactions in the optical spectra of single pairs of coupled QDs. The coupling can come about through exchange interactions if the wavefunctions in the neighboring QDs overlap.

Alternatively, long-range Coulomb interactions can provide the coupling, as when an exciton exerts a dipole interaction on excitons in other QDs. Moreover, if the QDs are incorporated into a 3D optical cavity, the dipole interaction between excitons can be increased in strength and range, as proposed by Atac Imamoglu of the University of California, Santa Barbara, and his collaborators. ¹³ However, for this approach to succeed, the QD and optical cavity must couple strongly. Strong coupling means that the coherent coupling strength between the cavity photon and the exciton is greater than the dephasing rate of either the photon or the exciton. The same requirement arises in attempts to harness the quantum coherence of the QD electron or exciton. Here, it also extends to the cavity photon. Strong coupling with a single QD remains an exciting challenge, but inserting QDs in cavities is important even in the weak coupling regime as a way to modify the spontaneous emission rate.

Material scientists will continue to create complex QD structures, such as QD molecules, and the variety of QD structures will continue to increase. Optical techniques, as they are further optimized, will continue to play a major role, not only in probing these engineered materials but also in dynamically controlling their electronic wavefunctions. Ultimately, it will prove possible to harness the full quantum mechanical wavefunction of a quantum nanostructure by means of a combination of nanostructure engineering and coherent external fields. New and possibly revolutionary quantum electronic technologies in the solid state will follow.