Noninvertible symmetries: What’s done cannot be undone

Symmetry has long been a foundational concept in theoretical physics and mathematics. It simplifies complex physical problems and reduces the number of unknown variables. You would have a nightmare, for example, solving the Schrödinger equation for the hydrogen atom in Cartesian coordinates x, y, and z. But the problem simplifies dramatically if you use spherical coordinates and leverage the atom’s rotational symmetry: The atom looks the same after it’s rotated about one of its axes. Symmetry not only helps unify and organize the fundamental forces of nature but also guides the search for new physics.

Symmetry transformations are those that leave a system looking and behaving the same. Conventional symmetry transformations are invertible. If we rotate a square by 90°, for example, the transformation can be undone by a −90° rotation. Such intuition is formulated rigorously by Wigner’s theorem, which implies that every symmetry transformation in quantum mechanics has an inverse. The mathematical language used to describe conventional symmetry transformations is called group theory, a foundational concept that has shaped modern physics for more than a century (see, for example, the article by Martin Rodriguez-Vega, Maia Vergniory, and Greg Fiete, Physics Today, May 2022, page 42 ).

One way only

In recent years, however, researchers have shown that the traditional notion of symmetry is too limited in quantum field theory and quantum many-body systems. A new class of symmetries—noninvertible—has been identified in various physical systems, including lattice models describing magnetism and quantum field theories of strong interactions between quarks. As the name suggests, noninvertible symmetries are implemented by transformations that do not have inverses—that is, what’s done cannot be undone.

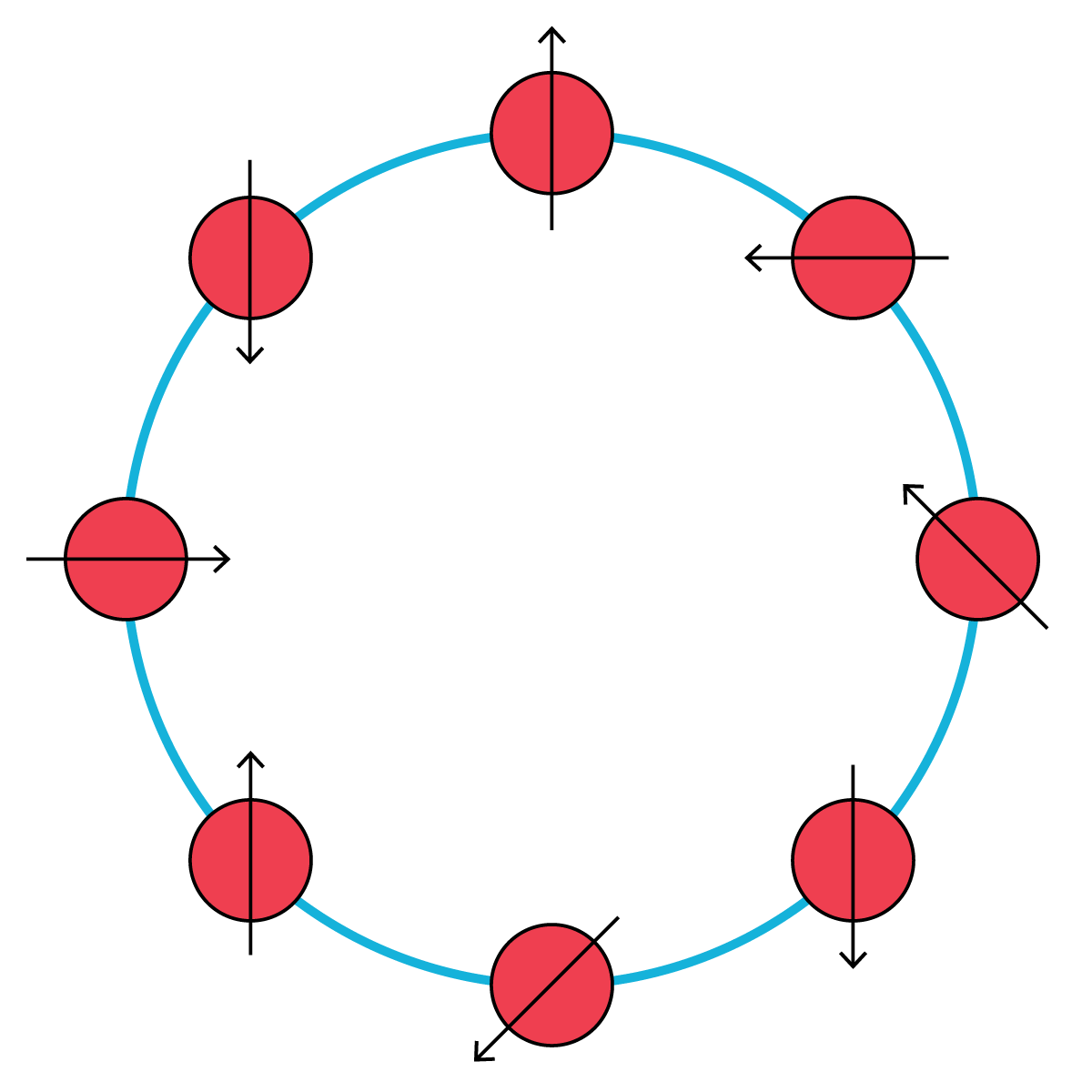
Figure 1.

The fundamental reason that symmetries can be noninvertible is quantum superposition. In deterministic classical physics, a cat is either alive or dead. In quantum physics, Schrödinger’s cat can be both alive and dead simultaneously. The wavefunction describing Schrödinger’s cat is a superposition of two individual wavefunctions—one for an alive cat and one for a dead cat. Superposition introduces more possibilities for symmetries in quantum physics: A symmetry transformation can cause the wavefunction of a single cat to become a superposition of two. If the transformation is repeated, the result is a superposition of increasingly many cat wavefunctions, and no inverse transformation reverts to a single cat.

As paradoxical as it may sound, the new symmetries lead to new conservation laws, which serve as novel tools to study strongly coupled physical systems. They also point to alternative physical models and beg for a new mathematical framework to describe symmetries in quantum physics.

Noninvertible symmetry of a magnet

Noninvertible symmetries already exist in physicists’ favorite toy model for ferromagnetism: the Ising model in one spatial dimension. The 1D model consists of an array of qubits placed on a circle, as illustrated in figure 1. Each qubit can be spin up $|\mathrm{\uparrow }⟩$, spin down $|\mathrm{\downarrow }⟩$, or any quantum superposition of the up and down states, such as $|\mathrm{\to }⟩\propto |\mathrm{\uparrow }⟩+|\mathrm{\downarrow }⟩$.

The state $|\mathrm{\uparrow }\mathrm{\uparrow }·\; ·\; ·\mathrm{\uparrow }⟩$, in which every spin is pointing up, corresponds to a magnet whose north pole is pointing up. Similarly, the state $|\mathrm{\downarrow }\mathrm{\downarrow }·\; ·\; ·\mathrm{\downarrow }⟩$ corresponds to a magnet whose south pole is pointing up. On the other hand, the state $$|\mathrm{\to }\mathrm{\to }·\; ·\; ·\mathrm{\to }⟩\propto |\mathrm{\uparrow }\mathrm{\uparrow }·\; ·\; ·\mathrm{\uparrow }⟩+|\mathrm{\downarrow }\mathrm{\uparrow }·\; ·\; ·\mathrm{\uparrow }⟩+|\mathrm{\uparrow }\mathrm{\downarrow }·\; ·\; ·\mathrm{\uparrow }⟩+·\; ·\; ·+|\mathrm{\downarrow }\mathrm{\downarrow }·\; ·\; ·\mathrm{\downarrow }⟩\text{(1)}$$ represents a superposition of all possible spin configurations. Since that is a state with no preference for spin up or spin down, magnetization is lost. The transition from $|\mathrm{\uparrow }\mathrm{\uparrow }·\; ·\; ·\mathrm{\uparrow }⟩$ to $|\mathrm{\to }\mathrm{\to }·\; ·\; ·\mathrm{\to }⟩$ models the process of heating up a magnet: As the temperature reaches a critical value, the magnet loses its magnetization.

Figure 2.

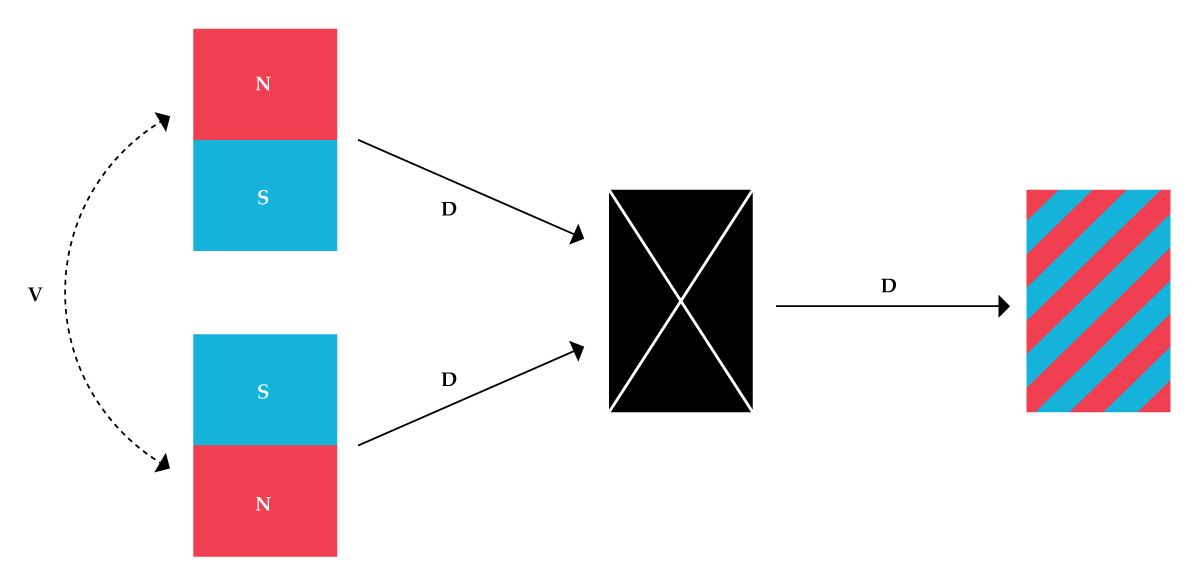
What are the symmetries in the toy model for a magnet? Because the north and south poles are on the same footing, an ordinary symmetry can transform one to the other. It flips all the spins from up to down and vice versa: $|\mathrm{\uparrow }\mathrm{\uparrow }·\; ·\; ·\mathrm{\uparrow }⟩\mathrm{\to }|\mathrm{\downarrow }\mathrm{\downarrow }·\; ·\; ·\mathrm{\downarrow }⟩\mathrm{\to }|\mathrm{\uparrow }\mathrm{\uparrow }·\; ·\; ·\mathrm{\uparrow }⟩$. That is an invertible symmetry—apply it twice, and we return to the starting point. The demagnetized state $|\mathrm{\to }\mathrm{\to }·\; ·\; ·\mathrm{\to }⟩$ is symmetric under the spin-flip symmetry because there is no notion of north versus south.

At the critical temperature, an additional symmetry emerges whose effect is $|\mathrm{\uparrow }\mathrm{\uparrow }·\; ·\; ·\mathrm{\uparrow }⟩\mathrm{\to }|\mathrm{\to }\mathrm{\to }·\; ·\; ·\mathrm{\to }⟩$ and $|\mathrm{\downarrow }\mathrm{\downarrow }·\; ·\; ·\mathrm{\downarrow }⟩\mathrm{\to }|\mathrm{\to }\mathrm{\to }·\; ·\; ·\mathrm{\to }⟩$. The additional symmetry transformation acts identically on the up and down states, as illustrated in figure 2. Whether the output state was initially in the up or down state before the transformation isn’t knowable. Relatedly, if we apply the transformation a second time, we find a superposition of up and down states: $|\mathrm{\to }\mathrm{\to }·\; ·\; ·\mathrm{\to }⟩\mathrm{\to }1/\sqrt{2}(|\mathrm{\uparrow }\mathrm{\uparrow }·\; ·\; ·\mathrm{\uparrow }⟩+|\mathrm{\downarrow }\mathrm{\downarrow }·\; ·\; ·\mathrm{\downarrow }⟩)$. The symmetry transformation cannot be inverted and thus it is a noninvertible symmetry.

The technical details

We now examine more carefully the noninvertible symmetry in the Ising model, which has $L$ qubits, labeled by $j$ = 1, 2, . . ., $L$, arranged on a 1D closed, periodic ring. (It has a counterpart in two dimensions. ¹ ) On each qubit, a quantum operator, denoted as $\mathbf{Z}$, can be applied to measure the spin: $\mathbf{Z}|\mathrm{\uparrow }⟩=+|\mathrm{\uparrow }⟩$, $\mathbf{Z}|\mathrm{\downarrow }⟩=-|\mathrm{\downarrow }⟩$. Alternatively, another quantum operator, denoted as $\mathbf{X}$, can be applied to flip the spin, where $\mathbf{X}|\mathrm{\uparrow }⟩=|\mathrm{\downarrow }⟩$, $\mathbf{X}|\mathrm{\downarrow }⟩=|\mathrm{\uparrow }⟩$.

If we represent a qubit’s spin-up and spin-down states as two column vectors, $\left(\begin{array}{c}1\\ 0\end{array}\right)$ and $\left(\begin{array}{c}0\\ 1\end{array}\right)$, then the operators become the Pauli matrices $\mathbf{Z}=\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right)$ and $\mathbf{X}=\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right)$. When we have multiple qubits, we can similarly define ${\mathbf{Z}}_j$ and ${\mathbf{X}}_j$ as operators that measure or flip the $j$th qubit while leaving the others unchanged.

In quantum mechanics, the time evolution of a system is governed by an operator called the Hamiltonian, which features in the Schrödinger equation. At the critical temperature, the Hamiltonian for the Ising model takes the form $$\mathbf{H}=-{\sum }_{j=1}^L{\mathbf{X}}_j-{\sum }_{j=1}^L{\mathbf{Z}}_j{\mathbf{Z}}_{j+1}\text{. (2)}$$

The first term models a transverse magnetic field, and the second term models the coupling between the spins of neighboring qubits.

What are the symmetries of the critical Ising model? A necessary condition for a symmetry is that it must lead to a transformation that leaves the Hamiltonian invariant. The Hamiltonian is invariant under the transformation ${\mathbf{X}}_j\mathrm{\to }{\mathbf{X}}_j$ and ${\mathbf{Z}}_j\mathrm{\to }-{\mathbf{Z}}_j$. That transformation is the spin-flip symmetry implemented by the operator $\mathbf{V}={\mathbf{X}}_1{\mathbf{X}}_2.\; .\; .{\mathbf{X}}_L$. It commutes with the Hamiltonian, which means that it does not change over time. In other words, it’s a conserved quantity.

Is there an additional symmetry in the Ising model? Another transformation that leaves the Hamiltonian invariant is $${\mathbf{X}}_j\mathrm{\to }{\mathbf{Z}}_j{\mathbf{Z}}_{j+1}\text{,}{\mathbf{Z}}_j{\mathbf{Z}}_{j+1}\mathrm{\to }{\mathbf{X}}_{j+1}\text{, (3)}$$ which is known as the Kramers–Wannier transformation. ² What exactly do the arrows in equation 3 mean? Even though the literature has commonly suggested that the Kramers–Wannier transformation is invertible, it’s not. To see why, let us assume that the transformation is implemented by conjugating an operator by an invertible operator $\mathbf{U}$. The Kramers–Wannier transformation would thus be written as $$\mathbf{U}{\mathbf{X}}_j{\mathbf{U}}^{-1}\stackrel{?}{=}{\mathbf{Z}}_j{\mathbf{Z}}_{j+1}\text{,}\mathbf{U}{\mathbf{Z}}_j{\mathbf{Z}}_{j+1}{\mathbf{U}}^{-1}\stackrel{?}{=}{\mathbf{X}}_{j+1}\text{. (4)}$$

Let us apply the invertible transformation on the spin-flip operator $\mathbf{V}$ of the Ising model: $\mathbf{U}\mathbf{V}{\mathbf{U}}^{-1}=\mathbf{U}({\mathbf{X}}_1{\mathbf{X}}_2.\; .\; .{\mathbf{X}}_L){\mathbf{U}}^{-1}=({\mathbf{Z}}_1{\mathbf{Z}}_2)({\mathbf{Z}}_2{\mathbf{Z}}_3).\; .\; .({\mathbf{Z}}_{\mathrm{L}}{\mathbf{Z}}_1)=1$, where in the last step, we have used ${{\mathbf{Z}}_j}^2$ = 1. When we multiply by ${\mathbf{U}}^{-1}$ from the left and $\mathbf{U}$ from the right, the spin-flip operator $\mathbf{V}$ becomes a trivial operator, which is a contradiction.

The Kramers–Wannier transformation, therefore, cannot be implemented by an invertible operator, as Wigner’s theorem suggests. Rather, the meaning behind the arrows in equation 3 is answered by the following operator $\mathbf{D}$: ³ $$\mathbf{D}=\underset{\underset{\text{invertible but not conserved}}{⏟}}{e^{-\frac{2\pi iL}{8}}\left(\prod _{j=1}^{L-1}{e}^{\frac{i\pi {\mathbf{X}}_j}{4}}{e}^{\frac{i\pi {\mathbf{Z}}_j{\mathbf{Z}}_{j+1}}{4}}\right)e^{\frac{i\pi {\mathbf{X}}_L}{4}}}\times \underset{\text{conserved but noninvertible}}{\underbrace{\frac{1+{\prod }_{j=1}^L{\mathbf{X}}_j}{2}}}\text{. (5)}$$

It is rather complicated, but the only thing we need to know is that $\mathbf{D}$ is a product of an invertible but not conserved operator and a conserved but noninvertible operator. Because of the second factor, $\mathbf{D}$ is a noninvertible matrix that has some zero eigenvalues. The noninvertible operator implements the Kramers–Wannier transformation in the following precise sense: $$\mathbf{D}{\mathbf{X}}_j={\mathbf{Z}}_j{\mathbf{Z}}_{j+1}\mathbf{D}\text{,}\mathbf{D}{\mathbf{Z}}_j{\mathbf{Z}}_{j+1}={\mathbf{X}}_{j+1}\mathbf{D}\text{. (6)}$$

Since ${\mathbf{D}}^{-1}$ does not exist, however, the equation cannot be written in the form of equation 4, and thus no contradiction exists. The operator commutes with the Hamiltonian, and it is therefore a conserved quantity that does not change over time. It is a noninvertible symmetry.

The square of an ordinary symmetry is another symmetry: If a 90° rotation is applied twice, the result is a 180° rotation. But what about for the noninvertible symmetry? From equation 4, we see that applying $\mathbf{D}$ twice moves ${\mathbf{X}}_j$ forward to site $j$ + 1. It appears that the noninvertible symmetry behaves like a lattice translation by half a site. That’s inaccurate, however: Nothing exists between two lattice sites!

In fact, the operator $\mathbf{D}$, the spin-flip operator $\mathbf{V}$, and the one-site lattice translation operator $\mathbf{T}$ obey the algebraic relation $\mathbf{D}\times \mathbf{D}=\mathbf{T}\times (1+\mathbf{V})/2$.

The action of $\mathbf{D}$ on a state, therefore, is conditioned on the response of that state to the spin-flip symmetry. The square of $\mathbf{D}$ corresponds to a one-site lattice translation $\mathbf{T}$ on states that are symmetric under $\mathbf{V}$, such as the state in equation 1. But it is zero on states that flip signs under $\mathbf{V}$. That algebra, which was recently derived, ³ does not fit in the mathematical framework of group theory and goes beyond the paradigm of Wigner’s theorem. The new, noninvertible symmetry brings fresh insights into physical systems more generally.

So what is it good for?

One important task in condensed-matter physics is to characterize the phase diagram of a physical system. A familiar example is water at atmospheric pressure, which has gas, liquid, and solid phases. The task is often challenging because of strong interactions among the microscopic particles and atoms. Symmetry provides one of the few powerful analytic tools available to study such strongly coupled systems.

In particular, the noninvertible symmetries of systems that are invariant under the Kramers–Wannier transformation bring fresh insights into quantum systems. In the critical Ising model and a large class of related models, for example, magnetization and demagnetization coexist, which implies nontrivial entanglement properties. A formalization of that intuition ^4–7 shows that the presence of a noninvertible symmetry forbids a featureless phase in which there is no entanglement. Moreover, the symmetry constrains the number of ground states with the lowest energy. Such a constraint would not have been possible if the Kramers–Wannier transformation were mistaken as an ordinary, invertible symmetry.

For many years, the discussion of noninvertible symmetries was confined to toy models in one spatial dimension, such as the Ising model for magnetization. A pair of papers ^{8 , 9} from a few years ago, however, led to many developments. Inspired by earlier work, ¹⁰ they introduced a construction of noninvertible symmetries applicable in three or more spatial dimensions. The key to the construction was the connection to another type of novel symmetry, known as the higher-form symmetry, that acts on extended objects such as strings. ¹¹

The ideas led to a rapid discovery of new symmetries across various physical systems, including quantum electrodynamics. ^{12 , 13} The symmetries provide tantalizing insights into other topics too, including particle physics; point to mistakes in the literature on scattering amplitudes; ¹⁴ and consolidate conjectures in quantum gravity and string theory. Beyond high-energy physics, noninvertible symmetries have also been applied to lattice models in condensed-matter theory and quantum information, which has led to the discovery of novel topological phases of quantum matter and constraints on phase diagrams. The new symmetries have emerged as a unifying language that brings together researchers of high-energy physics, condensed matter, and quantum information.

The idea of the noninvertible symmetry has emerged from interdisciplinary developments in physics and math. Because it goes beyond the framework of group theory, it calls for a new mathematical language. In some cases, the correct language has been identified as category theory, a generalization of group theory. Such advancements are fostering vibrant collaborations between mathematicians and physicists and mark a new chapter in the alignment of the two fields.

Throughout history, symmetries have contributed to major breakthroughs in physics. The symmetry discovered in 1941 by Kramers and Wannier ² is now understood as a special example of noninvertible symmetries, and it predicted the critical temperature of the Ising model. The result encouraged Lars Onsager in 1944 to find the exact solution of the Ising model. ¹⁵ In recent years, the discovery and application of new noninvertible symmetries has led to a wave of progress across various areas of physics, and many more promising breakthroughs are on the horizon.

This article was originally published online on 3 June 2025.