New Physics in Fusion Plasma Confinement

How does one confine a 100-million-degree plasma in the laboratory? Because charged particles tend to follow magnetic field lines, one can use a well-constructed magnetic field to isolate and insulate the plasma from its surroundings. If the constituent ions of a plasma are sufficiently reactive (for example, a mixture of deuterium and tritium), and if the isolated plasma is sufficiently hot and dense, nuclear fusion will occur. Should the plasma touch the wall of the containment vessel, it would instantly cool and pollute the bulk plasma with material from the wall.

The magnetic approach to fusion has already produced megawatts of fusion energy—an amount roughly comparable to the external heating supplied to the plasma. The international fusion research community is confident enough about the future of magnetic fusion to be planning experiments in which the fusion yields will exceed the external heating energy by factors of 10 or more. Such “burning” plasma experiments, for example the proposed International Thermonuclear Experimental Reactor (ITER), would constitute a major step on the path to commercial power production from fusion.

Underlying that confidence is a sequence of remarkable scientific discoveries about magnetized plasma behavior. Indeed, the past decade or two have delivered a striking change in perspective: Once seen as an intractable tangle, described at best by rough estimates and empirical scaling laws, a magnetized plasma is increasingly viewed as a fully comprehensible physical system whose detailed internal structure can be shaped by external manipulation.

The new perspective affects many aspects of fusion research. In this article, we focus on the historical challenges of fusion research: understanding and controlling transport (including particle diffusion, heat conduction, and similar processes), turbulence, and macroscopic plasma instabilities.

No confined plasma can be in thermodynamic equilibrium, and each departure from equilibrium provides a free energy source to drive instability. The instabilities that have most affected fusion progress are driven either by plasma currents or by plasma pressure gradients. Today, new methods exist for confining plasma without having to impose a current, thus eliminating the first free-energy source. In addition, ingenious confinement geometries—still in exploratory stages—can counteract the second.

Transport poses some of the most challenging issues in plasma dynamics because of its association with turbulence, self-organization, and other nonlinear processes. It has also produced some of the most startling surprises. Recent advances in the understanding and control of turbulence-driven transport are, as you will see, revolutionary.

Magnetic plasma confinement basics

So how is magnetized plasma confined in a torus? It begins with the confinement of magnetic field lines: One must devise field lines that remain on closed surfaces. Lines that chaotically explore a three-dimensional volume or wander off without bound are not very helpful. In the language of nonlinear dynamics, the desired field lines are bounded and integrable. The closed magnetic surfaces are usually covered by the quasiperiodic trajectory of a single field line. If the field does not vanish, then every magnetic surface within a torus must have toroidal topology and can be described with two angle coordinates: a poloidal angle, encircling the torus the short way, and a toroidal angle, measured with respect to an axis going through the hole in the torus (see figure 1). The coordinate that labels each magnetic surface is the minor radial coordinate r, which increases as one proceeds from the plasma core to the plasma boundary; thus, the radial direction points outward from the plasma core. The ratio of the major to minor radius, R/r, is the machine’s aspect ratio; the aspect ratio is large for a thin torus (as in figure 1) and small for a fat torus.

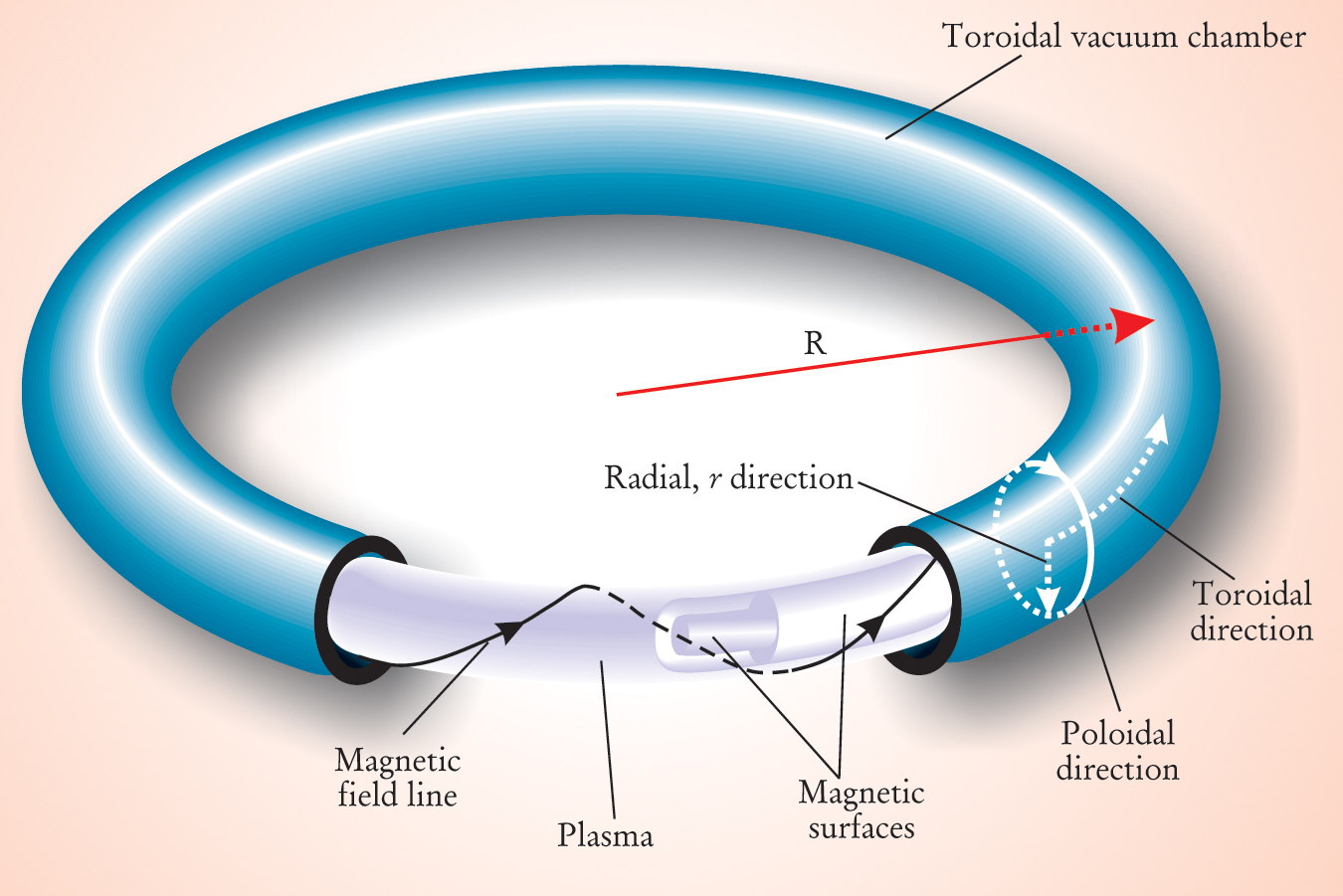
A confined field line is therefore one that winds around a torus on a single magnetic surface. The corresponding magnetic field has poloidal and toroidal components, denoted respectively by B _p and B _t, but no radial component. The relative change in the angular coordinates, averaged in an appropriate sense as one follows a field line, is the field-line pitch, and the rate at which that pitch changes from one magnetic surface to the next is the magnetic shear.

A confined magnetic field is useful because one can load it with charged particles. For a straight field line, each particle’s cyclotron motion (or gyration) keeps it within a Larmor radius (or gyroradius) of the line, and therefore close to a magnetic surface. As designers of particle accelerators well know, however, the motion of charged particles along curved, toroidal field lines is a little more complicated than that. Rather than gyrating strictly around a single field line, the particle’s guiding center (the center of its nearly circular orbit) can drift radially—for example, due to field curvature or field strength gradients. But it is not hard to construct field geometries for which even the guiding center’s motion is bounded and harmless. Charged particles moving under the influence of such a static, integrable magnetic field are confined.

This picture of magnetic confinement remains oversimplified because it considers the response of charged particles only to an imposed magnetic (or electric) field. Real charged particles interact with each other by creating their own electromagnetic fields. These self-generated fields can be either microscopic, when associated with individual particles, or macroscopic, when caused by collective processes. We next consider these individual and collective types of interaction.

Benign collisional transport

Plasma scientists have a good understanding of Coulomb collisions between charged particles, also called binary interactions or two-particle correlations. Indeed, plasma processes arising from Coulomb collisions, as opposed to collective plasma processes, are referred to as “classical.” The random changes in velocity due to collisions effectively cause particles to jump from one field line to another, as illustrated in figure 2. The resulting random walk leads to a radial heat diffusivity κ, estimated by $$\kappa \approx v{\Delta }^2,$$ (1) where v is the collision frequency and Δ is the radial step size. Only steps in the radial direction are significant for transport. For Coulomb collisions in a magnetized plasma, v becomes the Coulomb collision frequency v _C, and Δ is roughly the thermal gyroradius ρ $$\Delta \approx \rho =mv/qB,$$ (2) where m is the particle mass, q the charge, B the magnetic field strength, and v _t the thermal speed. Thus the classical diffusion coefficient is $${\kappa }_{\text{c}}\approx v_{\text{c}}{\rho }^2.$$ (3)

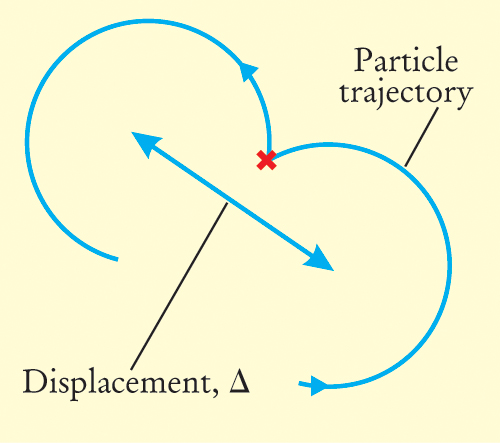
The Coulomb collision frequency, which decreases with plasma temperature, is very small in fusion-relevant plasmas, so classical diffusion is no obstacle to fusion.

In the late 1960s, researchers noticed that equation (3) is strictly correct only for the idealized case of straight field lines. Its deficiency for a torus is especially marked in very hot plasmas, where collisions only infrequently interrupt guiding-center motion. In those plasmas, a particle’s excursion away from a magnetic surface, measured by the width of the guiding-center orbit, is usually larger than a gyroradius. The resulting “neoclassical” transport theory differs from classical theory in several ways, but its main effect, crudely speaking, is to replace the ordinary gyroradius in equation (3) by the so-called poloidal gyroradius, in which the poloidal field component B_p replaces the total field B in equation (2). For those many devices in which B _p is an order of magnitude smaller than B, the neoclassical effect is a measurable enhancement of transport.

From the viewpoint of fusion confinement, however, both classical and neoclassical transport are benign. Both embody field fluctuations that arise from particle discreteness; the resulting irreducible fluctuation level is small enough to be harmless.

Malign turbulence

Neoclassical transport effects—diffusion, heat conduction, electrical conductivity, and so on—can be calculated more or less from first principles. The resulting literature, mostly from the 1970s and 1980s, presents a theoretical structure of considerable detail and breadth, but until quite recently it seemed sadly detached from experiment. The transport properties observed in confinement experiments consistently exceeded the neoclassical predictions by one or two orders of magnitude. The so-called “anomalous transport” was observed in virtually all plasmas.

The origin of the disparity lies in collective, turbulent motion, a form of charged-particle interaction much more virulent than binary Coulomb collisions. Turbulent transport is by no means a showstopper for magnetic confinement fusion, but it is potent enough to affect unfavorably the size and cost of a fusion reactor.

It is not surprising that a hot, confined plasma displays turbulent fluctuations. After all, such a plasma is a strongly driven system, whether heated by experimental artifice or by fusion reactions. It more often resembles a pot of merrily boiling water than it does the quietly simmering pool that neoclassical theory assumes. In fact, heat transport in a confined plasma resembles heat transport outward through the convection zone of the Sun.

One can crudely describe such transport using equation (1), by interpreting v as the inverse correlation time of the churning motion and Δ as its radial correlation width. The turbulent eddies in a magnetic confinement experiment are typically elongated along the magnetic field, but their radial widths are comparable to the Δ of collisional transport, the poloidal gyroradius (see figure 2). Far more distinctive in the turbulent case is the correlation time. Determined by the frequency of a typical microscopic instability, this time is orders of magnitude shorter than the Coulomb collision time, which accounts for the experimentally observed rapid heat conduction.

The main mechanism for charged-particle motion across the magnetic field is the so-called E × B velocity, for which the relevant electric field, as previously mentioned, can either be externally imposed or arise within the plasma. Hence turbulence in a magnetized plasma is characterized by strongly fluctuating E × B drifts; a turbulent velocity field in a magnetized plasma necessarily reflects a turbulent electromagnetic field. The dominant fluctuations are usually in the electric field, rather than in the magnetic field.

When the fluctuating E × B drift has a radial component and when such fluctuations have the proper phase relation to the density or pressure fluctuations of the turbulent plasma, there is a mean radial motion of the plasma toward the dangerous boundary of the confinement system.

Reducing electric field turbulence

The dominant role of turbulence in confined plasma transport seemed inevitable. Thus fusion scientists were startled by the discovery in Germany, in 1982, of a confinement regime in which the outer (large-r) part of the confined plasma was not turbulent. ¹ A sort of eerie quiescence settled over that outermost region of the plasma; interactions with the walls of the vessel were visibly reduced and global confinement was significantly improved. At the same time, the density and temperature gradients in this outer region became markedly steeper. The discoverers called this new regime the “high-confinement mode,” or H mode. Magnetic fusion scientists around the world, using machines of all kinds, quickly began reproducing and studying the details of H-mode operation.

It was soon noticed that the thin region of steep gradients and reduced turbulence—a toroidal annulus only a few centimeters thick, located near the outermost closed magnetic surface—had a strong radial electric field that varied sharply with radius throughout that region, and did not evolve during the high-confinement phase of the various experiments. Such a field—very strong only in a narrow region—in a magnetized plasma necessarily implies a strongly sheared E × B flow of the plasma: The flow can be either toroidal or poloidal and is nearly stationary in time. The experimental data in figure 3 show that the increase in the sheared E × B flow, a decrease in density fluctuations, and an increase in the pressure gradient all occur simultaneously.

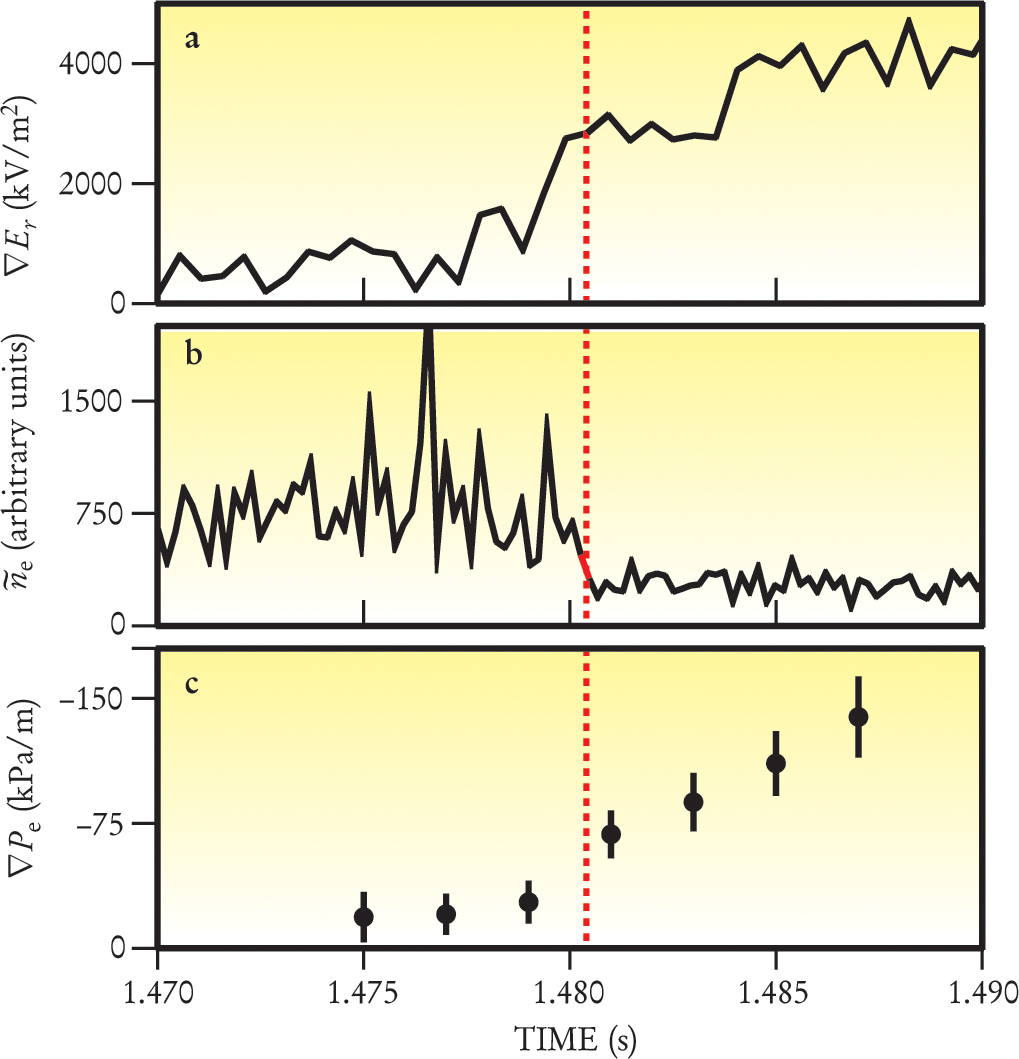
In short, the H-mode plasma is characterized by a barrier to diffusion and heat conduction in the form of a thin layer of sheared flow near its boundary. In effect, it’s another wall within the plasma. This idea of a transport barrier, erected with a radially sheared E × B flow, has now become a central theme of magnetic confinement physics. ²

Notice that turbulent plasma transport is both driven and inhibited by manifestations of the E × B drift. Fluctuating radial drifts, due to poloidal and toroidal electricfields, cause radial transport; relatively stationary poloidal or toroidal drifts, due to radial electric fields, form the transport barrier.

Internal transport barriers

Transport barriers have now been observed worldwide in many magnetic confinement devices. Experimental measurements have uncovered in considerable detail the temporal and spatial structure of barrier formation and evolution. Fusion scientists have also learned how to create such barriers by external manipulation. For example, appropriately injected beams of neutral atoms, which are unaffected by the magnetic field until they are ionized or undergo charge exchange, can create shear flow by collisionally inserting toroidal or poloidal momentum. Also, localized heating can indirectly affect the flow by modifying temperature profiles. Transport barriers have even been erected by using electrodes to impose electrostatic field structures directly.

In addition, fusion scientists can now place transport barriers at various radial locations within the confined plasma. Making such internal transport barriers requires modifying the magnetic field: An externally driven localized current first creates a narrow annulus across which the magnetic shear changes sign. The improved fluid stability associated with such regions causes a modest steepening of the fluid gradients, which in turn increases the flow shear through diamagnetic effects. The result can be the creation of a shear layer in the plasma core, similar to the barrier seen near the plasma edge in the original H mode. In particular, the internal shear layer displays the familiar dramatically steepened profiles of temperature and density.

Amazingly, under certain circumstances, the internal transport barrier can spread: The shear-flow region broadens radially to include a significant fraction of the plasma core. Throughout this sheared region, the ion temperature profile is roughly consistent with neoclassical transport. Thus, although neoclassical diffusion—much weaker than the anomalous diffusion—still lacks a definitive analytic treatment in regions of exceptionally low shear and strong electric field, the internal transport barrier may well provide its first experimental realization in a hot plasma.

One remaining challenge in these plasmas is to similarly improve confinement for the electrons. Because electrons have higher thermal speeds and smaller gyroradii than ions, their associated instabilities tend to occur on smaller temporal and spatial scales. The fast, fine-scale turbulence of electrons is less affected by velocity shear than is the ions’ turbulence, with the result that electron heat transport across an internal transport barrier can be substantial and relatively difficult to control.

A deeper look at barriers

Transport barriers maintained by shear flow are not unique to plasmas. They are, in fact, observed in a wide variety of physical systems, including hydrodynamical experiments and planetary atmospheres. ³ Nevertheless, the plasma case is distinctive in several respects, the most important of which is that shear flow in a plasma is intrinsically electromagnetic. Its electromagnetic nature provides unique hooks on which researchers can hang both high-resolution diagnostic instruments and external controls.

Researchers have used diagnostics like Doppler spectrometry and other techniques to examine not only the detailed timing of shear-flow creation and turbulence reduction, ² but also the character of the turbulence—correlation times, eddy structures, and so on. When such observations are coupled to increasingly mature theory and numerical simulation, a convincing picture of barrier formation and evolution emerges (along with an evolving list of unanswered questions and puzzling details). ⁴

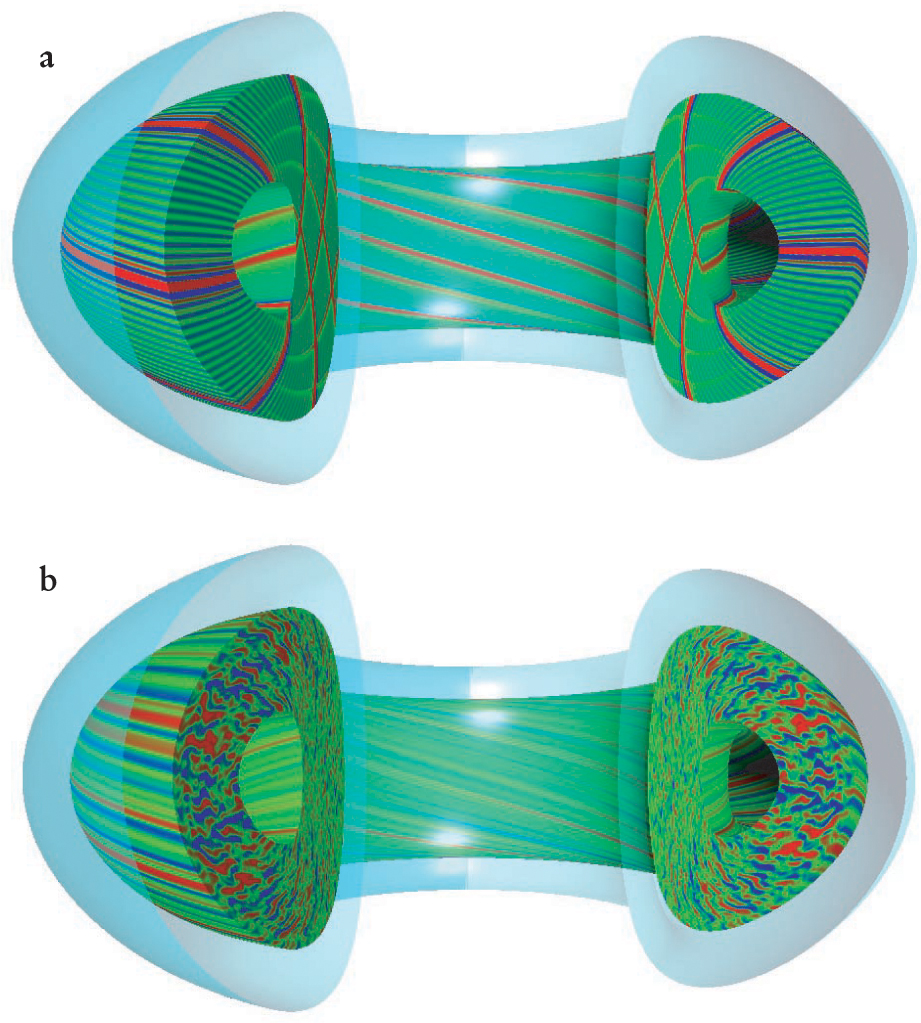
The shear-flow mechanism of transport reduction is nicely displayed by numerical simulations that use plasma kinetic theory. Figure 4 shows the equipotential surfaces found in one such simulation: plasma instability driven by a temperature gradient. As seen in figure 4(a), the instability first produces equipotential structures that are extended in two directions: along the equilibrium magnetic field lines and in the radial direction. The radial structure arises because field structures on neighboring magnetic surfaces are in similar environments and therefore align similarly. The extension of the equipotential surfaces in the radial direction corresponds to radial E × B motion and poor confinement. If the equipotential pattern shown in figure 4(a) were to persist, the plasma would rapidly reach the container’s wall and be lost. Instead, the plasma survives because the instability’s next phase generates a pattern of shear flow in the poloidal and toroidal directions. The effect of that flow, shown in figure 4(b), is to break up the radial convective structure and thereby reduce both the amplitude of the turbulence and the associated radial transport. In the case of a transport barrier, the reduced transport is even more pronounced, but sharply localized in radius.

The origin of shear flow is also increasingly well understood, even though several distinct mechanisms, including external momentum input and, near the plasma boundary, unbalanced charge loss, can play a role. Internal transport barriers, in particular, arise from nonlinear fluid convection known as Reynold’s stress. The associated poloidal and toroidal zonal flows are familiar from hydrodynamic research on their wind-current analogs on Earth and other planets. In the planetary case, the zones are bands of latitude characterized by a certain direction of the prevailing wind. In a magnetically confined plasma, the zones are toroidal annuli. Uniform on magnetic surfaces, zonal flows change swiftly in the radial direction, causing a corrugated flow pattern that is especially effective at reducing turbulent transport. These flows appear to underlie the observation of neoclassical heat conduction.

Reducing magnetic turbulence

The H mode reduces turbulence in the electric field. In those plasmas, the stabilizing presence of a strong magnetic field, produced by powerful magnets, keeps the turbulence in the magnetic field small. In an actual reactor, the magnets will be superconducting. Why not forgo these powerful magnets in favor of simpler, less expensive, weaker magnets? Historically, the answer has been that if the externally supplied magnetic field is weak compared to the field generated by plasma currents, then the magnetic field in the plasma becomes turbulent, displaying fluctuations in space and time. But that answer could be changing.

The magnitude of the magnetic field fluctuations is small—only about 1% of the total field. One might expect such “noise” in the field to be harmless. However, the magnetic noise has a huge effect on the trajectories of the field lines.

The magnetic fluctuations can be decomposed into a collection of waves—or Fourier modes—traveling in the poloidal and toroidal directions and standing in the radial direction. Despite its complexity, the turbulence contains a special property: a spatial resonance with the background magnetic field that exists in the absence of turbulence. A Fourier component of the fluctuating magnetic field will be nearly constant on a background field line whose pitch matches the structure of the component. For each such Fourier component, a magnetic surface with the corresponding field-line pitch is resonantly affected.

Thus, although most field lines are only slightly perturbed by the fluctuations, those on resonant surfaces are badly compromised, even to the point of losing their confined character. In the worst case, turbulence causes the resonating field lines to wander chaotically throughout the plasma volume, dragging charged particles along. The confinement of particles and energy is degraded.

The magnetic fluctuations are well described by the equations of magnetohydrodynamics (MHD), a coupled set of nonlinear equations in which the plasma is treated as a conducting fluid. MHD predicts a chaotic magnetic field, most easily viewed as a Poincaré plot of the intersections of magnetic field lines with a horizontal plane passing through the torus (figure 5(a)).

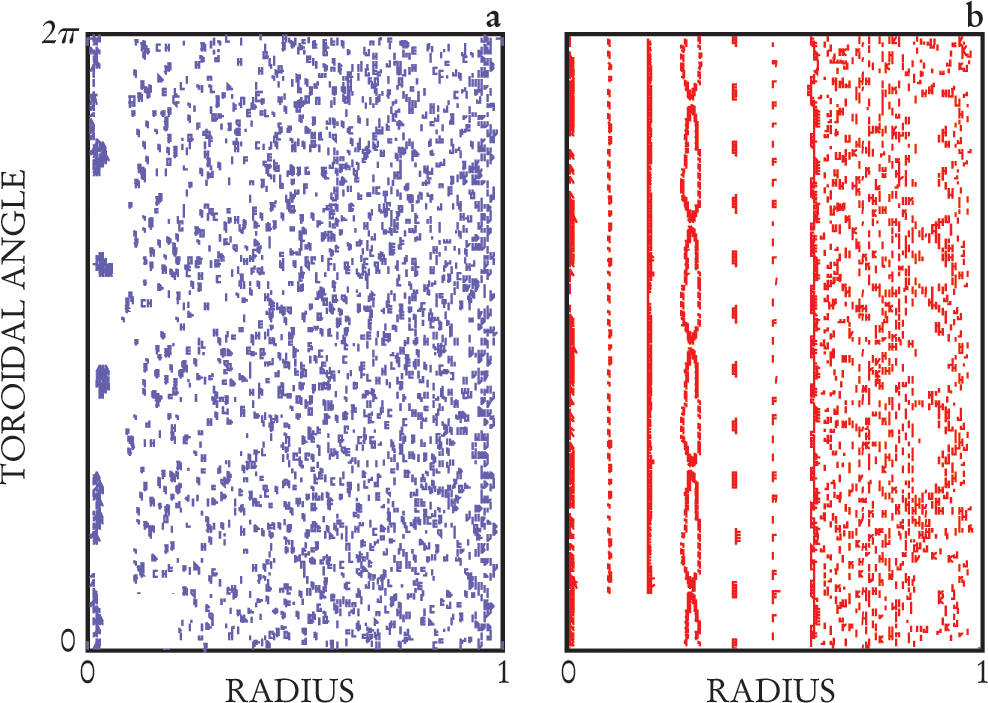
It is not a coincidence that the magnetic fluctuations resonate with the equilibrium magnetic field. The resonance is one way that the magnetic field self-organizes in response to a free-energy source. In this case, the free energy comes from spatial gradients in the current density. The chaotic wandering of the field reduces the current gradient and thereby relaxes the free-energy source. Unfortunately for fusion science, this process also transports energy from the plasma’s core to its surface.

However, it is now known that driving extra current in the plasma—to reduce the current-density gradients, the source of free energy—reduces the magnetic turbulence. Solutions of the MHD equations, with an extra term for the additional driven current, show that the turbulence and chaotic wander of the field are reduced (figure 5(b)).

Experimenters have now tested this idea. ⁵ By optimizing the applied electric field, they have reduced the plasma current gradients and roughly halved the magnitude of the magnetic turbulence. The seemingly small reduction of magnetic fluctuations from 1% to 0.5% has a large effect on the macroscopic plasma behavior: The plasma temperature doubles from 4 million K to 8 million K, and the energy transport rate decreases 10-fold.

Until recently, researchers viewed plasma configurations that have weak external magnetic fields as poor candidates for fusion energy, necessarily riddled with magnetic turbulence and poor confinement. But these recent results suggest otherwise. Such low-field configurations (known historically as reversed field pinches) would lessen the need for the powerful and expensive magnets that are essential for other approaches.

Higher pressure in a fatter torus

The preceding discussion treated energy transport arising from small-scale instabilities. But even without turbulence—even if only neoclassical transport were present—a confined plasma would still be subject to macroscopic instability that would limit fusion reactor performance. Controlling large-scale instability is another front in recent confinement advances.

Energy transport must be minimized so that the fusion power output can dominate over the energy input required to maintain the hot plasma. In addition, the plasma pressure must be maximized to increase the fusion power. But all plasmas have a pressure limit beyond which instabilities develop. Sometimes those instabilities are catastrophic, causing a rapid loss of energy and the end of the plasma. At other times, the instability simply provides an upper bound to the plasma pressure.

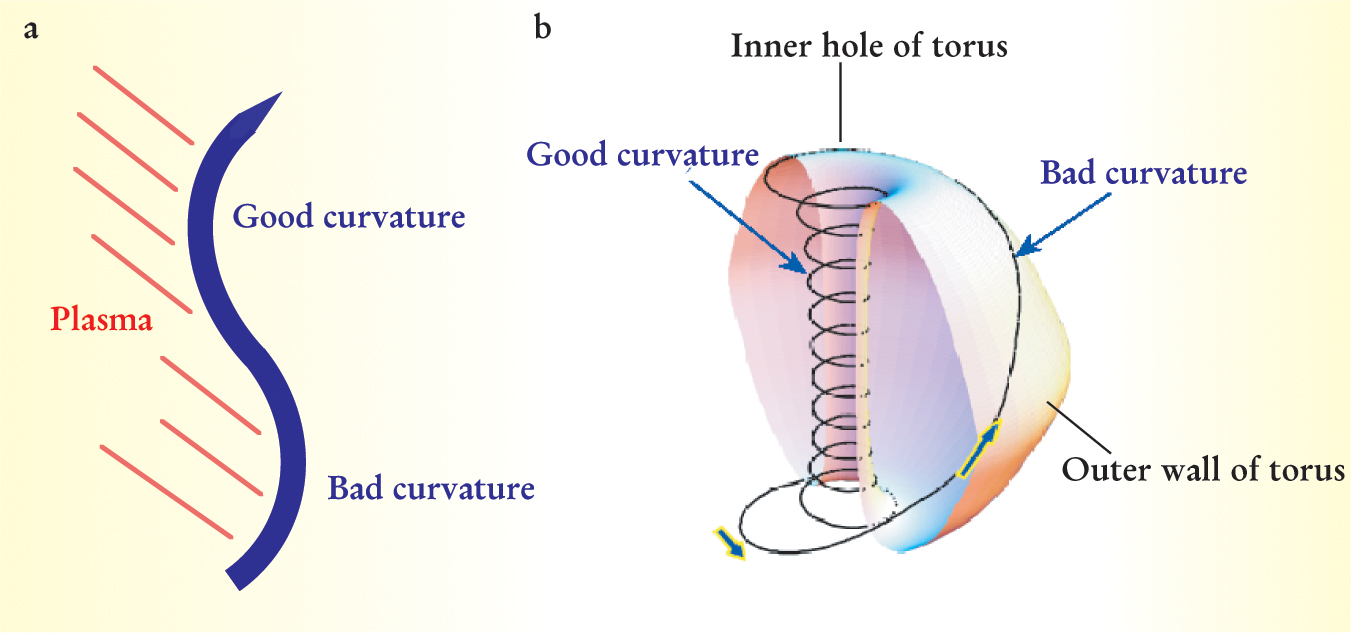
The most common form of pressure-driven instability is a magnetic analog to the well-known gravitational Rayleigh-Taylor instability that occurs when a heavy fluid rests on a lighter one. The gravitational force is negligible for laboratory plasmas, but the centrifugal force that particles experience as they move along a curved magnetic field acts like an effective gravitational force. The effective gravity is destabilizing if the magnetic field curvature is convex from the viewpoint of the plasma (figure 6(a)). If the curvature is concave, the effective gravity is stabilizing. In a plasma with a strong toroidal magnetic field, the curvature is mainly determined by that of the toroidal field. As a particle moves along a helical field line, it moves through a region of unfavorable destabilizing curvature on the large major radius side of the plasma, and a region of favorable curvature on the inner side. In a sense, the particles perform an averaging of the curvature, which ultimately determines the pressure limit.

If the aspect ratio of the torus is very small, say, approaching unity (a fat torus), the curvature properties are highly favorable, and very high plasma pressures can be maintained. ⁶ The trajectory of a magnetic field line in a low-aspect-ratio torus is shown in figure 6(b). The strength of the toroidal magnetic field decays inversely with distance from the major axis of the torus (as does the field from a straight wire). Hence the field line dwells in the inner region, where it has stabilizing curvature, and rapidly passes through the outer region of destabilizing curvature. A particle that follows the field line will average the curvature. Because it spends more time in the stable region, the plasma can achieve higher pressure.

The plasma pressure is expressed in terms of the dimensionless ratio, called β, of the plasma thermal pressure to the magnetic pressure. Higher β values allow a larger number of fusion reactions per unit of confining magnetic field. Experimental investigations of how β can be increased are under way in low-aspect-ratio tori, sometimes referred to as spherical tori or spherical tokamaks. (For another recent advance in increasing β, using a rotating plasma and active feedback, see Physics Today, September 2001, page 18 .)

New symmetries, no currents

The neoclassical theory of plasma transport was completed about 20 years ago—for the special, but important, case of a low-aspect-ratio plasma that is symmetric in the toroidal direction. The canonical toroidal angular momentum of a particle is then conserved, which provides a strong constraint on particle motion. If, however, the magnetic field lacks a direction of symmetry, that constraint is absent and the particle motion can be complex enough to both defy analytic treatment and challenge our intuition about collisional diffusion.

Recent analytic insights into particle diffusion in nonsymmetric plasmas, coupled with 3D computational treatment, have made possible a new class of confinement configurations ⁷ that are now beginning to be investigated experimentally (see Physics Today, June 2002, page 21 ). At first, these configurations are counterintuitive, as is immediately evident by glancing at the magnets used to produce the confining field. For a plasma symmetric in the toroidal direction, the magnet is a simple solenoid (figure 7(a)) producing a circular magnetic field that threads the plasma the long, toroidal way around. A toroidal current is then induced in the plasma, generating a poloidal magnetic field. The resulting field lines are helices that spiral through the torus as illustrated in figure 1. A beginning physics student can understand the magnetic field of a symmetric system. However, the magnets of the new nonsymmetric configurations (figure 7(b)) confound the most seasoned plasma machine builders. The coils appear to be twisted and malformed, each in a different way. Yet the coils, several meters in size, are precisely calculated and numerically machined to millimeter tolerance.

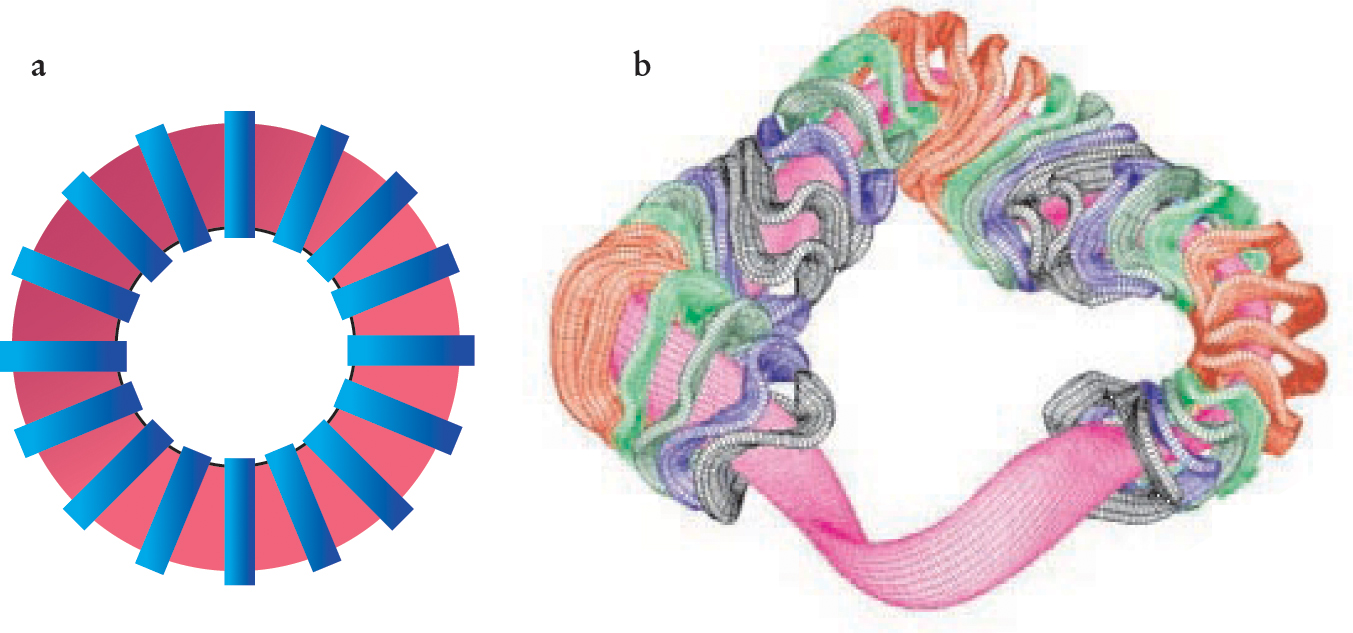
How do such asymmetric magnets produce a field that confines plasma? A key insight was that the particle trajectories remain close to magnetic surfaces whenever the magnitude of the magnetic field can be expressed in terms of a single angle variable on each surface: There must be one ignorable coordinate. Conventional axial symmetry achieves this simple dependence with a field that is independent of the toroidal angle. But orbit excursions can also be restricted by a more complicated symmetry: The field magnitude can have, for example, helical rather than circular symmetry. A further realization was that the symmetry need only be approximate; those systems are called quasi-symmetric. For example, the magnets shown in figure 7(b) produce a magnetic field whose magnitude is almost constant along a distorted helix. The result is that a charged particle will move along a well-confined trajectory within a highly asymmetric plasma. Amazingly, the collisional transport is small.

The new configurations are descendants of early asymmetric configurations known as stellarators, studied decades ago. Their development required not only the physical insights described here, but also new numerical techniques and modern computational power. These quasisymmetric stellarators may prove to be beneficial for fusion since current need not be driven in the plasma; the magnetic field can be created entirely by the magnets.

Changed pictures

The advances discussed here have affected the fusion community’s view of magnetic confinement and even of the very nature of magnetized plasma. A confined plasma has much more structure than the minimum imposed by magnetization: It is a self-organized nonlinear system. Previously, turbulence was considered a necessary companion of confined plasmas, as uncontrollable as the weather. Now we know that even turbulence can be tamed.

Advances in controlling plasmas have also affected conceptual designs for a fusion reactor. A reactor taking advantage of transport barriers, for example, could be smaller and less expensive than reactors imagined in 1980. At the same time, however, the traditional tasks required in a reactor—confining and heating plasma—would be supplemented by the need to maintain the barriers, perhaps by externally manipulating pressure and density profiles. As present experiments make the necessary external control seem more predictable and routine, the image of such an advanced reactor becomes more credible.

What is ahead for magnetic fusion research? One important challenge has already been mentioned: the experimental study of burning plasmas, in which the fusion power output greatly exceeds the power input. A second challenge is exploration of the broad spectrum of magnetic topologies that allow confinement—a challenge being faced at many laboratories worldwide. However, the crucial, underlying objective is to advance the scientific understanding of magnetized plasma behavior. The past few decades have taught no lesson more important than this: Fusion progress depends on progress in fundamental understanding.