Networks in motion
DOI: 10.1063/PT.3.1518
In 1991 sociologist Scott Feld wrote a scientific paper entitled “Why your friends have more friends than you do.” 1 Strange title for a paper, particularly because most of us do not perceive ourselves as any less popular than our friends. But according to Feld, if we could count the number of friends our friends have, most of us would find we come up short. Indeed, in any social group it can be proven that the average number of friends of friends is larger than or equal to the average number of friends; the equality holds only for the special case in which every person has exactly the same number of friends.
Far from a mere curiosity, this apparent friendship paradox is intimately related to the percolation properties of networks. For example, if a contagious disease propagates through a social network, one way to curb the spread would be to immunize a randomly selected fraction of the population. A far more effective strategy, however, would be to immunize not the selected people but an acquaintance of each of them.
2
A recent study appears to bear out that strategy: Researchers followed the spread of the H1N1 flu three years ago in two groups of college students—one group randomly selected, the other composed of friends named by the first group—and found that the number of flu cases peaked about two weeks earlier in the group of friends (see PHYSICS TODAY, November 2010, page 15
The issue originally studied by Feld is, in fact, just one of many broadly significant ones—including self-organization, information flow, and systemic robustness—that can now be properly formalized within the emerging theory of complex networks. Such issues are not unique to social networks and become more intriguing when they involve a reciprocal influence between the network’s structure and dynamical processes that take place on the network. For example, the island fox is a species unique to California’s Channel Islands. About 150 years ago, feral pigs were introduced onto the islands and, in the absence of natural predators, their population grew quickly. Although the pigs did not interact directly with foxes, the increase in pig population was accompanied by a crash in the fox population. Golden eagles were the reason: Attracted by the abundance of pigs to prey on, they had colonized the islands and begun preying on foxes as well, bringing them to near extinction. 3
Solving the problem—even in a network made up of just three species—turned out to be more complex than just redressing its primary cause. Removing the pigs, researchers realized, would prompt the eagles—a legally protected species—to prey more aggressively on the already endangered fox. In the end, conservationists mounted a coordinated removal of two species.
What then can we say about large networks, whose structure and dynamics are more complex still and can exhibit other unforeseen phenomena? Networks appear in widely disparate fields, as figure 1 illustrates. But a fundamental feature they share is that interactions between component parts can be just as important as the parts themselves in defining the properties of the system.

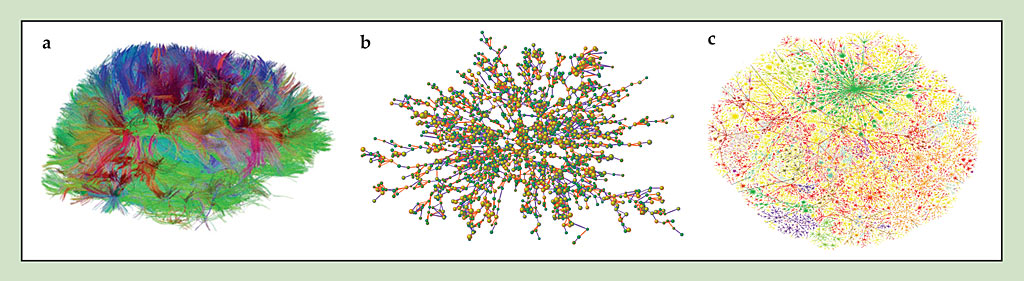
Figure 1. A gallery of networks.(a) The wiring of an adult human brain. Each colored line, resolved using diffusion spectrum imaging, represents a bundle of nerve fibers. (Courtesy of Van Wedeen, Harvard University.) (b) A social network used to establish the social influence of body weight. Yellow nodes correspond to obese people, with a body-mass index greater than 30. (Adapted from N. A. Christakis, J. H. Fowler, N. Engl. J. Med. 357, 370, 2007.) (c) Part of the network of major internet service providers, colored by IP. (Courtesy of Bill Cheswick and Hal Burch, Lucent Technologies.)
The notion that the interaction network matters has long been appreciated in physics. Indeed, different allotropic materials, such as graphite and diamond, are essentially different networks composed of the same atoms. But many more possibilities arise in networks of interacting organisms, computers, power stations, genes, and financial institutions, whose structures differ considerably from the picture suggested by regular (or even disordered) local arrangements. Such networks are not constrained to merely local interactions between nodes. They are also heterogeneous, particularly with respect to the nature and strength of the interactions—and to the number of interactions per node, also known as the degree k.
Take the case of sparsely connected, random networks. If the distribution of degrees for uniformly selected nodes is P(k), the distribution of degrees for their network neighbors will be proportional to kP(k). That proportionality to degrees, incidentally, is the basis of the sampling bias identified in networks of friends. But most real networks, however complex, are not random. In fact, a substantial part of the recent interest in network research concerns the modeling of salient characteristics that make them different from random. And the extent to which a complex network deviates from random provides insights into its organization, evolution, and function. 4
Physicists get real
Nearly 15 years ago, theorists discovered that empirical networks share seemingly ubiquitous structural properties. In particular, they found that numerous networks, including the internet, human-contact networks, air-transportation networks, and metabolic networks, are scale free—that is, they exhibit an approximately power-law distribution of degrees with a divergent variance. They also exhibit small-world features, in which most of the nodes are not neighbors of each other and yet can be reached from every other node through a short sequence of steps (see the article by Mark Newman in PHYSICS TODAY, November 2008, page 33
It wasn’t long before researchers began identifying dynamical implications. An early landmark was the demonstration that, for the simplest epidemic models, uncorrelated scale-free networks can exhibit a vanishing epidemic threshold in the limit of large population size, 5 meaning that viruses or other agents with arbitrarily low spreading rates can persist in the population. That demonstration exposed a previously unknown relation between network scaling and the vulnerability of human, animal, and computer networks.
The study of networks is not new, of course. Food webs, social networks, and intracellular pathways have long been topics of research. The novelty lies in scale and complexity: The current science of networks is fueled by the availability of vast amounts of information about them. In particular, the wealth of data allows researchers to apply statistical-physics and nonlinear-dynamics methods to make predictions or forestall problems. It also inspires theoretical studies, as illustrated in the box on
Self-sustained dynamics
Collective behavior manifests itself in many forms in networks—bursting neurons, phase-locked power generators, and schooling fish, among others. A number of these processes can be idealized as manifestations of spontaneous synchronization, a phenomenon in which different elements of the network stay in sync with each other in a decentralized way. To address the question of what network properties lead to such emergent behavior, researchers have turned to simplified models amenable to mathematical analysis. The best known of them is the Kuramoto model—a minimal representation of a large population of coupled oscillators, a model subsequently shown to be equivalent to certain arrays of Josephson junctions. 6
If each oscillator is coupled to all the others, there exists a critical coupling strength Kc > 0 above which a finite fraction of the network synchronizes. That phase transition is similar to a percolation transition, outlined in the box. In particular, as the coupling strength K is further increased, so is the number of oscillators recruited by the synchronous cluster. The problem becomes much more involved as soon as the network is allowed to be more general than the case of all-to-all coupling. For example, the question of whether Kc is finite or zero in scale-free networks remains unsettled. Mean-field calculations suggest it should vanish, numerical simulations are more consistent with its being strictly positive, 7 and an exact solution seems hard to come by with existing mathematical techniques.
In part because of those and other difficulties, researchers have focused on networks of identical or nearly identical nodes, particularly using the Pecora–Carroll model, which assumes the nodes are coupled by diffusive interactions. 7 Based on that model it can be shown, for instance, that heterogeneity in either the nodes or their connections generally inhibits their synchronization. Similar inhibition is caused by the presence of negative coupling strengths, which effectively repel the states of the connected nodes, and by a number of other network properties. Recently, however, one of us (Motter) and Takashi Nishikawa have demonstrated that the different synchronization-inhibiting properties, when they coexist in the same network, can compensate for each other and combine their effects in a way that actually facilitates synchronization. 8 Such behavior comes entirely from collective interactions and cannot be anticipated from pairwise interactions between two nodes in the network.
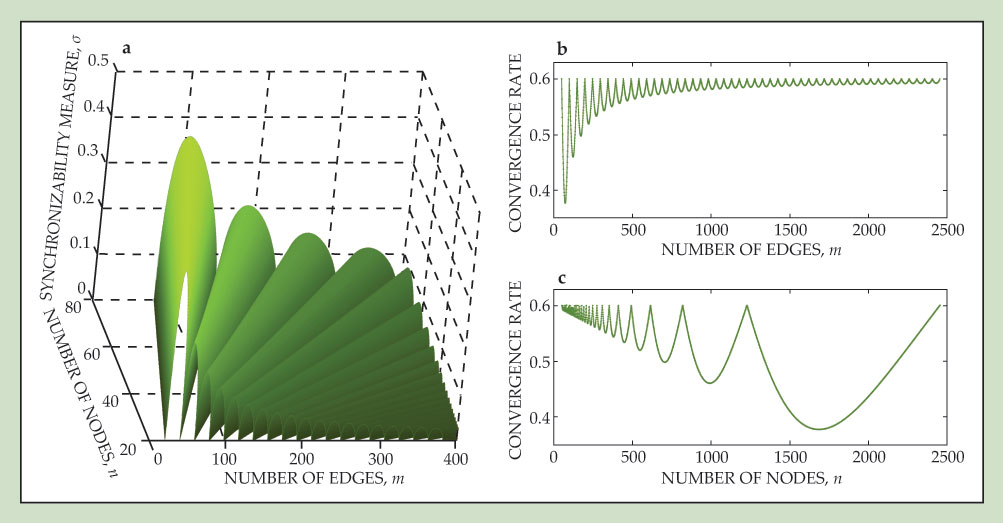
A related analysis also provides insight on the number of nodes that can engage in a given activity. Surprisingly, even when the network loses synchrony as the number of nodes is increased, it may regain synchrony when that number is further increased. Another fundamental result is that when the network structure is optimized for a given dynamical function, it often exhibits a cuspy landscape in the space of all possible networks, as pictured in figure 2. The implication is that a small change in the network structure—for instance, a modification in the strength of an edge—can lead to a very different dynamical behavior of the system as a whole. 8 That sensitive dependence of the network’s collective dynamics on its structural parameters can thus be interpreted as a network analog of chaos.

Figure 2. A landscape of networks that optimize synchronizability. (a) The structure of a network can be represented as a coupling matrix. The standard deviation σ of its eigenvalues is a measure of the propensity of the network’s nodes to synchronize. The figure plots the minimum value of σ from all the possible networks of n nodes and m edges. The smaller the σ at any point on the landscape, the more stable the synchronous state of those networks. Synchronization is thus most stable along cusps, where the derivatives of σ with respect to m and n both diverge. (b) The corresponding rate of convergence to a synchronous state, plotted as a function of the number of edges for networks of 50 nodes, exhibits highly nonmonotonic behavior. (c) When plotted as a function of node number for networks of 50 × 49 edges, the convergence rate behaves differently but again nonmonotonically. As nodes are added, the convergence rate falls, only to rise again as yet more nodes are connected. (Adapted from ref.
Spreading out
A different class of processes concerns the dynamics of spreading through a network. Innovations diffuse; fads develop; diseases are transmitted; failures propagate. Many such processes can be conceptualized either as epidemic-type dynamics, where a node in an infected state may infect a neighbor independently of the status of the other nodes, or as cascading-type dynamics, where the change in the state of a node may depend on the reinforcement caused by changes in other nodes. In both cases, the research focus is on the chain of events that takes place as the spreading unfolds and its relation to the properties of the system.
Researchers are gaining a deeper understanding of malware spread through the internet, for instance, thanks to the observation that the network’s scale-free distribution of degrees largely determines the nagging persistence of computer viruses. 5 Conducting analogous studies of spreading in human populations remains difficult due to the significantly more challenging task of tracking human mobility. That challenge is gradually being overcome, however, through complementary approaches. 9 Some of those approaches focus on the global transportation of passengers and have demonstrated the dominant role of air transportation in the spread of infectious diseases such as SARS (severe acute respiratory syndrome). Other approaches infer human-contact patterns by exploiting cell-phone data and currency-tracking games, such as Where’s George. The research is likely to provide new insights into the role of social networks in the spread of diseases; it may, in particular, yield a better understanding of how awareness of the presence of a disease changes people’s behavior and the possible outcome of an imminent outbreak.
The study of cascading processes, on the other hand, has provided insights into what determines rare but large events. The threshold model introduced by Duncan Watts a decade ago has been key. It assumes that the change in the state of a node from normal to modified—representing, for example, a failure or a change of opinion—depends on the fraction of neighbors that have already changed state. 10 In its simplest form, the network is assumed to be random with a given degree distribution and a given distribution of state transition thresholds, where the threshold of a node is the fraction of modified neighbors necessary for the node to change state.
Starting out with only one or a few seed nodes in the modified state, a macroscopic fraction of a large network changes to the modified state if and only if

where P(k) is the probability that a node has degree k, ρk is the probability that a degree-k node will change state—and thus be an early follower—if just one of its neighbors does, and z is the average degree in the network. The vulnerability of the network to large cascades increases with increased heterogeneity of the thresholds and decreases with increased heterogeneity of the degrees (unless the seed nodes are purposely taken among the hubs). In the hypothetical limit in which all nodes are early followers (ρk = 1 for all k), the equation above reduces to the condition required for the network itself to have a macroscopic connected cluster. Exactly what happens, though, may vary when other factors come into play; for example, cascades that develop in one network—the power grid, say—can influence the evolution of cascades in another, such as the internet or a telephone network. 11 In any case, one point is clear: The properties of the underlying network explain how a particular event can trigger a large cascade while many seemingly equivalent events have negligible consequences. It all depends on whether the triggering event hits a percolating cluster of early followers.
Biological dynamics
Living cells provide outstanding examples of collective behavior underpinned by networks of interactions. Molecular-level networks coordinate countless biological functions and allow the cells to respond to ever-changing environments. A newly encountered signal, such as excess sodium, may propagate through the network and alter cellular behavior. But even in the absence of external signals, interactions among genes and proteins can lead to multiple steady-state and dynamic equilibria. Also known as attractors, those equilibrium states can be thought of as the set of stable orbits toward which the system’s behavior converges over time, much as a gently nudged pendulum settles into one of many possible orbits.
The emergent dynamics of cellular networks have been on physicists’ minds since the late 1960s, when Stuart Kauffman introduced random Boolean networks as simple, prototypical models of collective behavior.
12
Although the initial models included unrealistic assumptions and led to results that did not stand the test of time, they paint a compelling picture: The dynamics of biological networks are poised near the boundary between the two extremes of frozen (that is, steady-state) and chaotic dynamics. That property of the dynamics is preserved as more realistic assumptions about the structure of the underlying network, or the logic of regulatory relationships, are made (see the Reference Frame by Leo Kadanoff in PHYSICS TODAY, March 2009, page 8
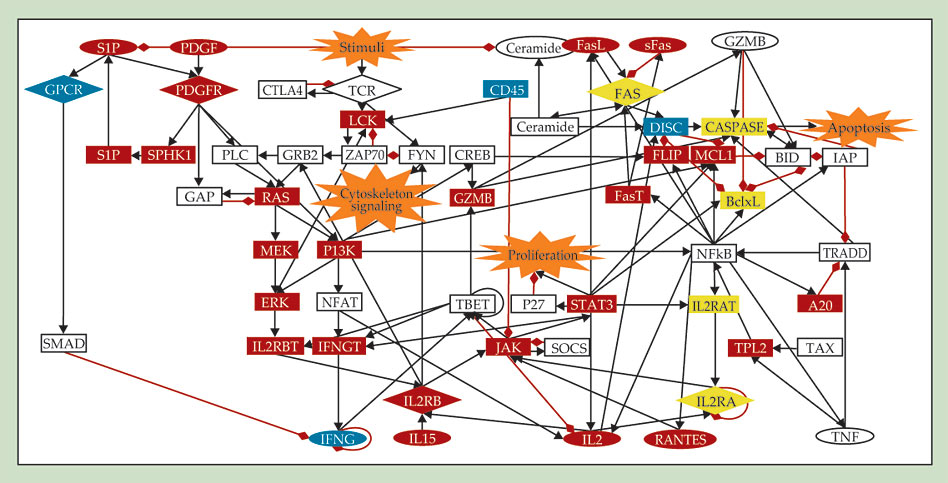
Genome-wide experimental methods now identify interactions among thousands of components. However, progress toward understanding the collective behavior emerging from the networks has been slow. The reason is that quantitative characterization of every reaction that participates in even a relatively simple function of a single cell often requires a decades-long effort. In that context, the Boolean models strike a balance between economy and realism for researchers striving to describe real biological processes, from cell differentiation and embryonic development to the programmed cell death pictured in figure 3. Moreover, experiments have already validated many of the models’ predictions, such as the effects of certain node disruptions on biological networks. 13

Figure 3. The signaling network of a T cell responsible for its programmed death (apoptosis). T cells participate in immune responses and depend on this network, which is activated by environmental stimuli, to control their population. Nodes represent proteins, and the directed edges (red or black) indicate the interactions between them. Boolean modeling reveals that targeting certain proteins, such as IL15, PDGF, and NFkB, can inhibit the abnormal survival of T cells that causes a form of blood cancer. (Adapted from ref.
Recent work on Boolean dynamic models has focused on the potential effects of stochasticity and uncertainty on the predicted attractors. For example, adapting the models to capture the observed variability in the duration of biological processes, represented as edges in the interaction network, reduces the total number of attractors but does not affect the steady-state attractors. The majority of cellular behaviors are indeed steady states or trajectories toward a steady state. This suggests that robustness to variability in timing is a general characteristic of biological systems that the models should also exhibit.
Controlling the damage
Networks can evolve or be designed to operate stably, but that stability may be lost when they are perturbed. Most previous studies of postperturbation control have focused on epidemiological problems. Recent studies indicate, however, that network failures as diverse as those underlying financial crises, power outages, and genetic diseases can also be ameliorated. Because most of the large-scale damage is often determined by the cumulative effect of the spread of failures rather than by any isolated event, that damage may be largely controllable even after the perturbation that causes it—a bankruptcy, malfunction, or mutation—has already hit the system.
One promising approach consists in exploiting the existence of multiple stable states inherent to a large number of complex networks. 14 For example, perturbed food webs can suffer extinction cascades, whereby the extinction of one species drives the extinctions of others. But the targeted suppression of specific species can direct a network to a new stable state in which most or all species survive. Analogously, living cells that are unable to reproduce due to the presence of faulty metabolic pathways can in principle be rescued, if not completely cured, by rebalancing the metabolic fluxes through the targeted suppression of specific genes. Similar genetic interventions can even make certain cancers disappear, by producing another stable but healthy state in the cells.
Beyond such examples of natural networks, researchers expect that self-healing technological networks, such as “smart” power-grid networks, may be within reach. And although a big gap exists between the theoretical and the practical, the possibility of recovering from failures in real time may also have implications for how best to control financial crises.
A broader view
Much of contemporary physics is based on the paradigm that macroscopic phenomena do not depend on the microscopic details of the process. They do depend, however, on the underlying network of interactions. With the prevalence of networked technologies, people—including physicists—are now predisposed to recognizing the importance of network concepts.
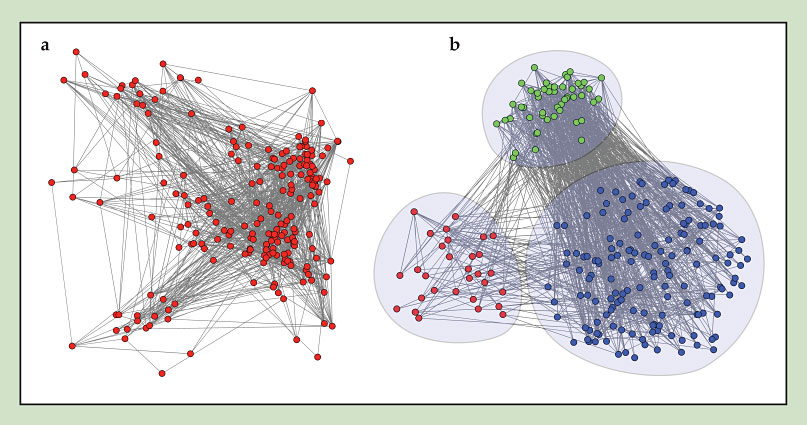
The network enterprise largely concerns the identification and analysis of network features relevant to a particular phenomenon. But with so many conceivable possibilities, what if we simply fail to look for the right features? It so happens that researchers have been thinking about that too. In the case of purely structural features, they have devised two exploratory methods that can identify patterns not anticipated by preconceptions. 15 One is based on maximum-likelihood techniques and the other on an integrative visual-analytics approach; both methods attempt to resolve the internal structure of complex networks by organizing the nodes into groups that share something in common, even if that thing is unknown a priori. Figure 4 gives an example. A broader undertaking for future research concerns the development of such exploratory approaches that can also systematically account for dynamical behavior.

Figure 4. Resolving internal network organization reveals hidden structural patterns. (a) Given this arbitrary network, a visual-analytics method identifies three groups of nodes that share common structural properties, without specific prior knowledge about the number of groups or what defines the groups. The method starts from a high-dimensional “node property space” that summarizes all relevant node properties and then takes multiple two-dimensional projections from that space. The projections can be inspected by eye and the nodes recursively parsed into groups clustered around common properties. (b) Posteriori inspection of the groups reveals that they are defined by lower-degree nodes with lower-degree neighbors (red), lower-degree nodes with higher-degree neighbors (blue), and higher-degree nodes (green); hence they cannot be resolved by a single node property. (Adapted from ref.
Beyond their efforts to reduce complexity and understand the workings of existing networks, scientists should exploit that understanding to build things. Still nascent fields, such as synthetic biology and microfluidics, could be revolutionized by rational circuit design, for instance. Materials research and other classical topics could also benefit from network theory. Recent progress in metamaterials is a case in point. Metamaterials often exhibit negative refractive indices, acoustic shielding, and other properties not found in conventional materials (see, for example, the article by Martin Wegener and Stefan Linden in PHYSICS TODAY, October 2010, page 32
The quest for how quantitative changes in network structure, scale, and components lead to qualitative changes is an overarching theme of current research. In retrospect, that theme epitomizes much of Philip Anderson’s classic essay “More is different” on the hierarchical structure of science, 16 but now from the vantage point of network theory.
Box. The physics of connectedness
The structure of a network is often regarded as a collection of dots connected by lines, where the elements of a network are represented by the dots, or nodes, and the interactions between them by the lines, or edges, as illustrated in figure 1. A fundamental question concerns the loss of interconnectivity upon the sequential removal of nodes or edges. In the control of an epidemic, for example, targeted immunization is more efficient than random immunization because the removal of highly connected nodes is generally more effective in fragmenting the network.
Equally important is the reverse process: the emergence of large-scale connectivity via, for example, the addition of edges. In the simplest case, the Erdős–Rényi random-graph model, one starts with a large number N of isolated nodes and adds one edge at a time between pairs of randomly selected nodes. A percolation transition appears when, in the limit of large N, a finite fraction of the network becomes connected. The transition occurs when the ratio r = m/N, defined by the number of edges m relative to the number of nodes, reaches a critical value rc = 1⁄2. Just below that point, the sizes of the connected clusters follow a power-law distribution, with the largest of order log N. Just above it, the size of the largest component is of order N and grows linearly with ∣r − rc∣.
The percolation transition process thus shares properties with many continuous phase transitions in physical systems. But as one changes the rules by which edges are added to the network, the transition point can appear earlier (that is, rc < 1⁄2 ), or later (rc > 1⁄2). The latter, in particular, leads to interesting new transitions dubbed “explosive percolation” because of their steep, seemingly discontinuous nature. 17 Such transitions have been studied in detail for so-called Achlioptas processes, in which two edges are generated at each step but only the edge that minimizes the growth of the clusters is kept. The resulting delay causes the transitions to be sharper when they occur. Rigorous analyses have shown 17 that they are, nonetheless, smooth, but described by nonanalytic scaling functions; the initial growth of the largest component scales with ∣r − rc∣β, where β ≪ 1.
Explosive percolations illustrate the impact of nonlocal information in the assignment of edges. And they have implications for spreading processes in a network. One might purposefully reduce the incidence of small events—power outages, say—but inadvertently at the price of the sudden emergence of larger ones.
References
1. S. L. Feld, Am. J. Sociol. 96, 1464 (1991). https://doi.org/10.1086/229693
2. R. Cohen, S. Havlin, D. ben-Avraham, Phys. Rev. Lett. 91, 247901 (2003). https://doi.org/10.1103/PhysRevLett.91.247901
3. F. Courchamp, R. Woodroffe, G. Roemer, Science 302, 1532 (2003). https://doi.org/10.1126/science.1089492
4. For further reading, see R. Cohen, S. Havlin, Complex Networks: Structure, Robustness and Function, Cambridge U. Press, New York (2010), and
A. Barrat, M. Barthélemy, A. Vespignani, Dynamical Processes on Complex Networks, Cambridge U. Press, New York (2008).5. R. Pastor-Satorras, A. Vespignani, Phys. Rev. Lett. 86, 3200 (2001). https://doi.org/10.1103/PhysRevLett.86.3200
6. S. H. Strogatz, Physica D 143, 1 (2000). https://doi.org/10.1016/S0167-2789(00)00094-4
7. S. N. Dorogovtsev, A. V. Goltsev, J. F. F. Mendes, Rev. Mod. Phys. 80, 1275 (2008). https://doi.org/10.1103/RevModPhys.80.1275
8. T. Nishikawa, A. E. Motter, Proc. Natl. Acad. Sci. USA 107, 10342 (2010). https://doi.org/10.1073/pnas.0912444107
9. V. Colizza et al., Proc. Natl. Acad. Sci. USA 103, 2015 (2006); https://doi.org/10.1073/pnas.0510525103
M. C. González, C. A. Hidalgo, A.-L. Barabási, Nature 453, 779 (2008); https://doi.org/10.1038/nature06958
D. Brockmann, L. Hufnagel, T. Geisel, Nature 439, 462 (2006). https://doi.org/10.1038/nature0429210. D. J. Watts, Proc. Natl. Acad. Sci. USA 99, 5766 (2002). https://doi.org/10.1073/pnas.082090499
11. S. V. Buldyrev et al., Nature 464, 1025 (2010). https://doi.org/10.1038/nature08932
12. S. A. Kauffman, The Origins of Order: Self-Organization and Selection in Evolution, Oxford U. Press, New York (1993).
13. R. Zhang et al., Proc. Natl. Acad. Sci. USA 105, 16308 (2008); https://doi.org/10.1073/pnas.0806447105
J. Saez-Rodriguez et al., PLoS Comput. Biol. 3(8), e163 (2007); https://doi.org/10.1371/journal.pcbi.0030163
O. Sahin et al., BMC Syst. Biol. 3, 1 (2009). https://doi.org/10.1186/1752-0509-3-114. S. Sahasrabudhe, A. E. Motter, Nat. Commun. 2, 170 (2011); https://doi.org/10.1038/ncomms1163
A. E. Motter, et al., Mol. Syst. Biol. 4, 168 (2008);https://doi.org/10.1038/msb.2008.1
A. Saadatpour et al., PLoS Comput. Biol. 7(11), e1002267 (2011). https://doi.org/10.1371/journal.pcbi.100226715. M. E. J. Newman, E. A. Leicht, Proc. Natl. Acad. Sci. USA 104, 9564 (2007); https://doi.org/10.1073/pnas.0610537104
T. Nishikawa, A. E. Motter, Sci. Rep. 1, 151 (2011).https://doi.org/10.1038/srep0015116. P. W. Anderson, Science 177, 393 (1972). https://doi.org/10.1126/science.177.4047.393
17. D. Achlioptas, R. M. D’Souza, J. Spencer, Science 323, 1453 (2009); https://doi.org/10.1126/science.1167782
R. A. da Costa et al., Phys. Rev. Lett. 105, 255701 (2010); https://doi.org/10.1103/PhysRevLett.105.255701
P. Grassberger et al., Phys. Rev. Lett. 106, 225701 (2011); https://doi.org/10.1103/PhysRevLett.106.225701
O. Riordan, L. Warnke, Science 333, 322 (2011). https://doi.org/10.1126/science.1206241
More about the authors
Adilson Motter is the Harold and Virginia Anderson Professor of Physics and Astronomy at Northwestern University in Evanston, Illinois, and Réka Albert is a professor of physics and biology at the Pennsylvania State University in University Park.




