Multistability and unpredictability

Decision making can be tough. Transferring the choice to an unbiased authority, like a coin or a die, may help to relieve the pressure. Indeed, for just a few dollars, you can buy a decision-making toy (see figure 1), consisting of a rigid rod and three magnets typically labeled with different outcomes: yes, no, and maybe. Just pull the rod away from equilibrium and let it swing erratically until it points to the answer. The whimsical pendulum makes the choice for you.

Figure 1.

Nevertheless, issues arise when you apply a bit of physical reasoning. The equations of motion of such a magnetic pendulum can be easily derived through consideration of the attractive force between the magnet and the rod. ¹ Given the initial conditions, those deterministic equations will precisely predict where the pendulum will end up. Therefore, you are actually the one making the decision, on the basis of your particular choice of initial conditions! In fact, you could place the rod very close to your secretly desired outcome, but that feels too much like cheating. So how much control do you really have over the final outcome?

It is a fun mathematical problem to consider, but the principles can be applied to more than just toys. Any system with multiple stable outcomes that are determined by the initial conditions is known as a multistable system. Such systems have historically been modeled by nonlinear equations of motion and solved with numerical methods. Yet even small errors in the initial conditions—due, perhaps, to finite numerical precision—can lead to significantly different predictions in chaotic systems. Statistics textbooks often use rolling dice or flipping coins as examples of randomness for that reason: Although in principle their motion can be described by classical mechanics, ² the precise initial conditions affect the final stable outcome.

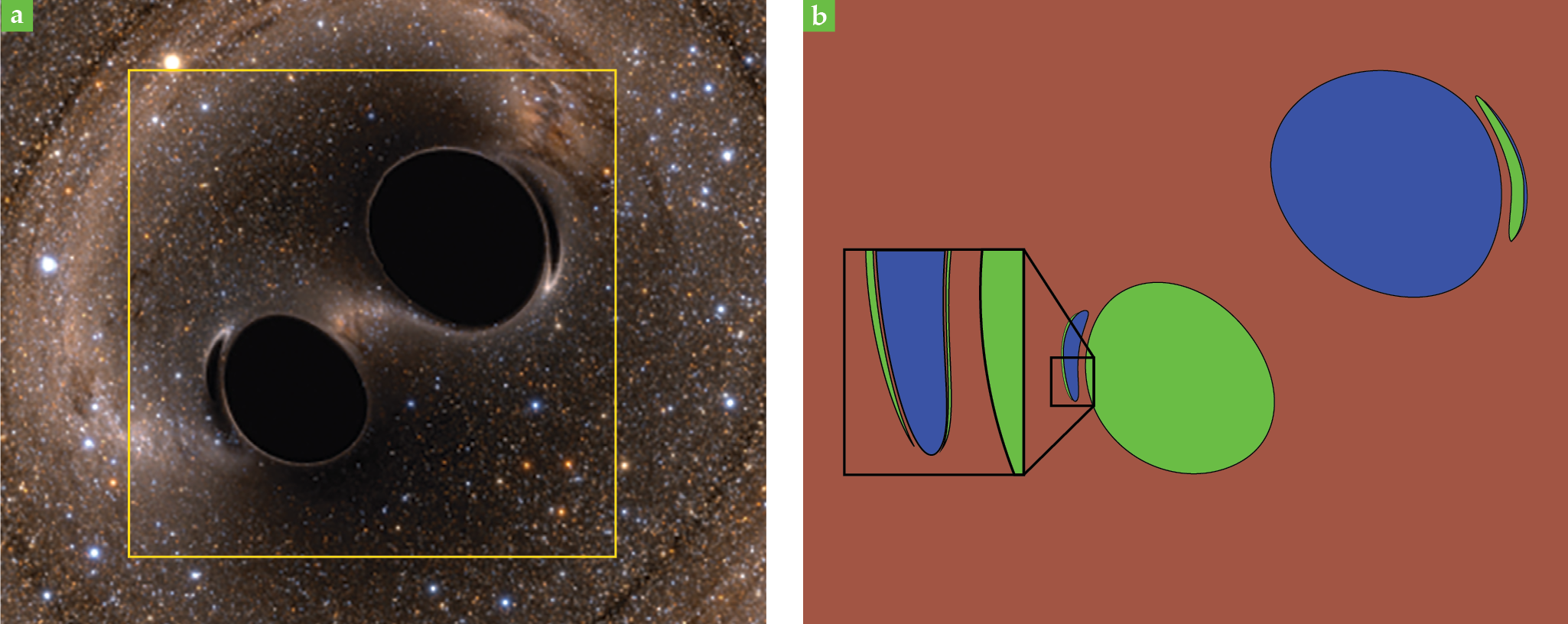
Multistability is found in many areas of physics, ranging from the quantum world to general relativity, spanning basic probability and complex atmospheric models. Indeed, the inherent nonlinearities of Albert Einstein’s field equations often lead to multistable situations. ³ For example, when two black holes orbit each other, the path of light around them is complicated by the competing gravitational wells and is difficult to predict. As illustrated in figure 2, photons face three possible outcomes in that scenario: being absorbed by black hole one, being absorbed by black hole two, or escaping. Although photons around binary black holes differ significantly from magnetic pendulums, the two systems share several defining features.

Figure 2.

Multistable systems pop up in other scientific disciplines too. The genetic toggle switch is a gene-regulation mechanism that tends to the expressed or silenced state, depending on the initial concentrations of proteins. ⁴ Such simple motifs allow for the construction of complex regulatory networks. The analysis of the system’s multistability may lead to a better understanding of gene expression.

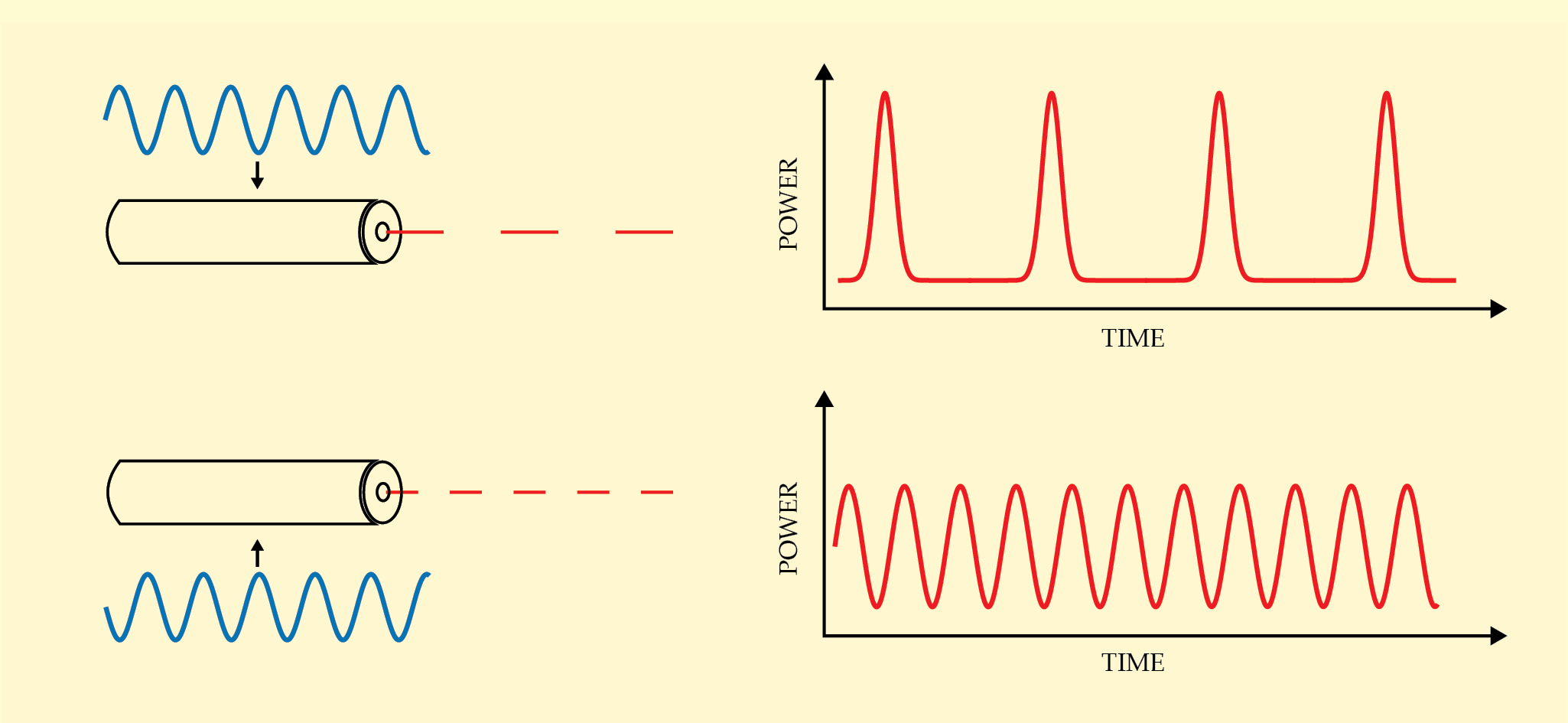
Asymptotic states are not limited to steady states. Complex scenarios can include periodic or even chaotic orbits. For instance, the multiple stable solutions of a swinging bell ⁵ are various modes of oscillation. And figure 3 illustrates the pulsating modes of a modulated laser, which depend on the initial conditions. ⁶ In general, if any characteristics allow us to distinguish between different asymptotic states, then we can and apply the theoretical framework of multistability. ⁷

Figure 3.

Fractal basins of attraction

One approach to investigating the behavior of multistable systems is building a map connecting initial conditions to their final outcome. Such a map is known as the basins of attraction. In figure 1, for example, the decision-making pendulum will come to rest above the yellow answer if it is released from the yellow basin of attraction. The term is borrowed from hydrology, in which a river basin is the area of land where rainfall ultimately gathers in a particular body of water. In nonlinear systems, the inherent unpredictability often results in intricate, sometimes even fractal, basin shapes. (Various basins of attraction adorn this article.)

When a basin of attraction has a fractal boundary, common intuition regarding outcome predictability is useless. ⁸ That is what allows a system like the decision-making pendulum to appear random. In a system with smooth basin boundaries, an enhancement in the precision of initial conditions by a factor of 10 yields a corresponding improvement in the overall predictability of the system. For fractal basins, increasing the precision 10-fold may result in only a two- or threefold improvement in predictions, or in extreme cases, no improvement at all. That scenario recurs at every scale because of the self-repeating nature of fractals.

Fractals are widely recognized for their complex structure across all scales and their noninteger dimensions (see the box below). The conventional topological dimension can be understood as the number of coordinates required to determine a point within an object: One coordinate is adequate for defining a position on a curve, two coordinates suffice for a point residing on a surface, and so forth. The fractal dimension generalizes the concept and offers insight into how extensively an object occupies space. For instance, a plane curve with a fractal dimension of 1.53 occupies more space than a line but less than a surface. The number is a proxy to describe how close we are to those limiting cases.

Nonetheless, the peculiarities of fractal boundaries extend beyond self-similarity and noninteger dimensions. They are just the tip of the iceberg, since the array of fractal basins encompasses extraordinary phenomena with fundamental implications for predictability.

Fractal dimension

The concept of dimension is more complex than what is taught in school. In fact, dimension can be calculated using a constructive approach called the box-counting method. It involves overlaying a grid of boxes of side length ε on a set of interest and counting the number of boxes N(ε) that contain some part of the set. The process is repeated with a series of decreasing values of ε. The value of N(ε) is expected to increase as ε decreases. In fact, N(ε) is proportional to ε^-d for small ε, where d is the box-counting—that is, fractal—dimension of the set.

For simple Euclidean sets like line segments and disks, the box-counting method may seem unnecessary because their dimensions are already known (1 for a segment, 2 for a disk). For more-complex geometric objects, such as fractals, the method becomes extremely useful.

Fractals are geometrically complex sets that have a noninteger dimension. An example of a fractal object is the boundary between Hudson Bay and Atlantic Ocean drainage basins. The draining of different geographic positions into distinct basins resembles the sensitive dependence of outcomes on initial conditions in a dynamical system.

This series of maps illustrates the application of the box-counting algorithm to the basin boundary (red). Each time we double the resolution, the number of boxes (gray) covering the curve increases. Continuing the process to very small values of ε, we can find a scaling law in which the exponent gives the fractal dimension of the curve.

In general, fractals have a fractal dimension greater than their topological dimension (1 for a line) but smaller than the dimension of the space in which they are embedded (2 for a surface). Multistable systems often present basins of attraction with fractal boundaries, which have fundamental consequences for the system’s predictability.

Cataloging unpredictability

Typically, boundaries divide two regions, as a border between countries does. Occasionally, isolated points separate more than two regions—for example, Four Corners marks the boundary point between Arizona, Utah, Colorado, and New Mexico. Points like that have a higher level of unpredictability, and a deviation from the exact boundary point can have more than two possible outcomes: For example, someone at Four Corners who gets pushed down could end up in any of the four states. What happens when a boundary is composed entirely of such points? Although such a boundary may seem implausible, fractal objects often challenge conventional understanding.

In the early 20th century, Japanese topologist Takeo Wada proposed a method for creating such a mind-boggling structure: three connected sets with a common boundary. Wada basins, named after him, refer to three or more fractal basins separated by a single boundary. That topological property is not just a fanciful oddity; Wada basins are ubiquitous even in simple systems, such as a damped pendulum subjected to continuous forcing. ⁸

Wada basins are not the basins with the most unpredictability. Some fractal curves, such as Peano curves and Hilbert curves, can fill the space. A boundary occupying the whole space means that the slightest uncertainty will lead to an unknown outcome. Despite being deterministic and regardless of how much the precision is improved, the system will always be unpredictable. Scenarios like that are modeled by what are known as riddled basins. In a way, riddled basins can be considered a bridge between determinism and randomness. In addition to Wada and riddled basins, multistable systems give rise to many more peculiar species, including sporadically fractal basins, intermingled basins, and basins with tentacles. ⁹

Usually, one of the first steps in analyzing a dynamic process involves allowing the state to evolve until an asymptotic behavior is recognized. A decision-making pendulum can still be moving slightly when it becomes clear which marked magnet the pendulum will stop above. Trials with different initial conditions may uncover alternative outcomes. Nonetheless, in some systems, that process is far from trivial, since the basins of the system can be hidden. ¹⁰ That situation arises when the basins are located away from their corresponding outcomes and there are no transient processes leading to them. The detection of such elusive basins requires special procedures.

Basins located close to their corresponding attractor can also be problematic when those attractors are found everywhere. Extreme multistability ¹¹ can arise when conservative chaos meets small dissipation; it leads to an overwhelming quantity of different attractors. Indeed, an arbitrarily large number of attractors can arise in that kind of situation. Still, manipulation of the system allows for custom-made scenarios of multistability. Two peculiar examples of such are megastability ¹² and matryoshka multistability, ¹³ in which attractors are nested and form an onion-like structure.

Furthermore, changing the parameters of the object of inquiry sometimes gives birth to two possible outcomes, an event called bifurcation. The same system may present a huge variety of situations depending on its precise parameters. The rich diversity of basins and associated phenomena are why creating tools to understand their unpredictability and classify them is necessary.

The multistability toolkit

The most straightforward method to quantify the unpredictability associated with basins is measuring their relative volume. Consider a loaded die for which the basin of one face occupies a volume 20 times as great as the volume of all the other faces combined. Clearly, a die will land with the biased face up most of the time. That simple measure, known as basin stability, ¹⁴ has been successfully applied to the characterization of multistable networks and high-dimensional systems, such as atmospheric models.

But basins are much more than just their size. Equivalent basin volumes in two systems do not necessarily imply the same predictability for both. Not only does the basin volume matter, but its morphology does also. For example, a bistable system with symmetric basins separated by a smooth boundary (imagine a two-by-two chessboard) and a system with riddled boundaries (imagine TV static) can present identical volumes. Even though the basin stability is the same in both cases, the situations are very different. The basin entropy, ¹⁵ a recently developed tool, incorporates both aspects to provide a quantitative measure of uncertainty.

Basin entropy can be understood as a nonlinear combination of multiple factors, including the fractal dimension of the boundaries and the number of attractors within a basin. In that way, the entropy accounts for the basin’s morphology and allows for the creation of a rational taxonomy. ¹⁶ For example, Wada basins maximize the number of attractors separated by the boundary, while riddled basins maximize the fractal dimension. Beyond quantifying asymptotic unpredictability in multistable systems, the basin entropy also quantifies fractal boundaries, bifurcations, and other defining characteristics.

Yet we are not simply doomed to observe the complexity of multistable systems; we can attempt to tame it. ¹⁷ You might find yourself trapped in one state but want to transition to another. In such cases, it is crucial to determine the minimal perturbation needed to move the system out of a basin of attraction. Interestingly, that minimal action provides yet another measure of the sensitivity associated with the basins. Instead of taking a static approach, you can use a carefully timed perturbation to drive the evolving trajectory from one asymptotic state to another. Regardless of the method, once the optimal window is identified, an external control can lead the system to the desired state. But how to make that optimum perturbation may not be known a priori. Alternatively, other techniques bypass that difficulty by employing feedback methods.

Delving into the realm of multistability transforms our perception of everyday objects and unveils a world of new possibilities. This article began with a discussion of a frivolous decision-making toy, but an understanding of multistability is pivotal in advanced topics such as neuroscience. ¹⁸ By leveraging the vocabulary derived from the study of nonlinear dynamics—akin to equations of motion governing a simple pendulum—we can gain a deeper understanding of the intricate mechanisms underlying cognitive choices. The interplay among attractors in multistable systems mirrors the complex cognitive processes at play when individuals navigate decisions.

Multistability is a prevalent phenomenon observed across various realms of physics, including classical mechanics, quantum mechanics, and cosmology. Its pervasive nature highlights its significance in unraveling the complexities of physical phenomena across different scales and domains. Insights derived from the study of elementary dynamical systems often have profound implications for addressing challenges encountered in diverse fields. The lessons learned in simple systems provide valuable perspectives and methodological approaches that offer fresh insights into long-standing questions across physics. Thus, the exploration of multistability not only enriches our understanding of fundamental physics but also fosters interdisciplinary synergies.