Lorentz Invariance on Trial
DOI: 10.1063/1.1784301
The null result of the celebrated 1887 Michelson–Morley experiment was surprising and difficult to explain in terms of then prevalent physics concepts. It required a fundamental change in the notions of space and time and was finally explained, almost 20 years later, by Albert Einstein’s special theory of relativity. (See the May 1987 special issue of
Experimental techniques introduced throughout the 20th century led to continued improvements in tests of special relativity. For example, 25 years ago, Alain Brillet and John L. Hall used a helium–neon laser mounted on a rotary platform to improve the accuracy of the Michelson–Morley experiment by a factor of 4000. In addition to the Michelson–Morley experiments that look for an anisotropy in the speed of light, two other types of experiments have constrained deviations from special relativity. Kennedy–Thorndike experiments search for a dependence of the speed of light on the lab’s velocity relative to a preferred frame, and Ives–Stilwell experiments test special relativistic time dilation.
In 1960, Vernon Hughes and coworkers and, independently, Ron Drever conducted a different kind of Lorentz invariance test. 1 They measured the nuclear spin precession frequency in lithium-7 and looked for changes in frequency or linewidth as the direction of the magnetic field rotated, together with Earth, relative to a galactic reference frame. Such measurements, known as Hughes–Drever experiments, have been interpreted, for example, in terms of a possible difference between the speed of light and the limiting velocity of massive particles. 2
Why bother?
Theorists and experimentalists in disciplines ranging from atomic physics to cosmology have been increasingly interested in tests of Lorentz invariance. The high sensitivity of experimental tests combined with recent advances in their theoretical interpretation allows one to probe ultrashort distance scales well beyond the reach of conventional particle-collider experiments. In fact, both the best experiments and astrophysical observations can indirectly probe distance scales as short as the Planck length
The breaking of Lorentz symmetry enables the
Cosmology provides an additional important impetus to look for violations of Lorentz symmetry. The recognition that the universe is dominated by dark energy suggests a new field—known as quintessence—that permeates all space. The interaction of that field with matter would manifest itself as an apparent breaking of Lorentz symmetry.
It could be argued on aesthetic grounds that the Lorentz and
Effective field theory
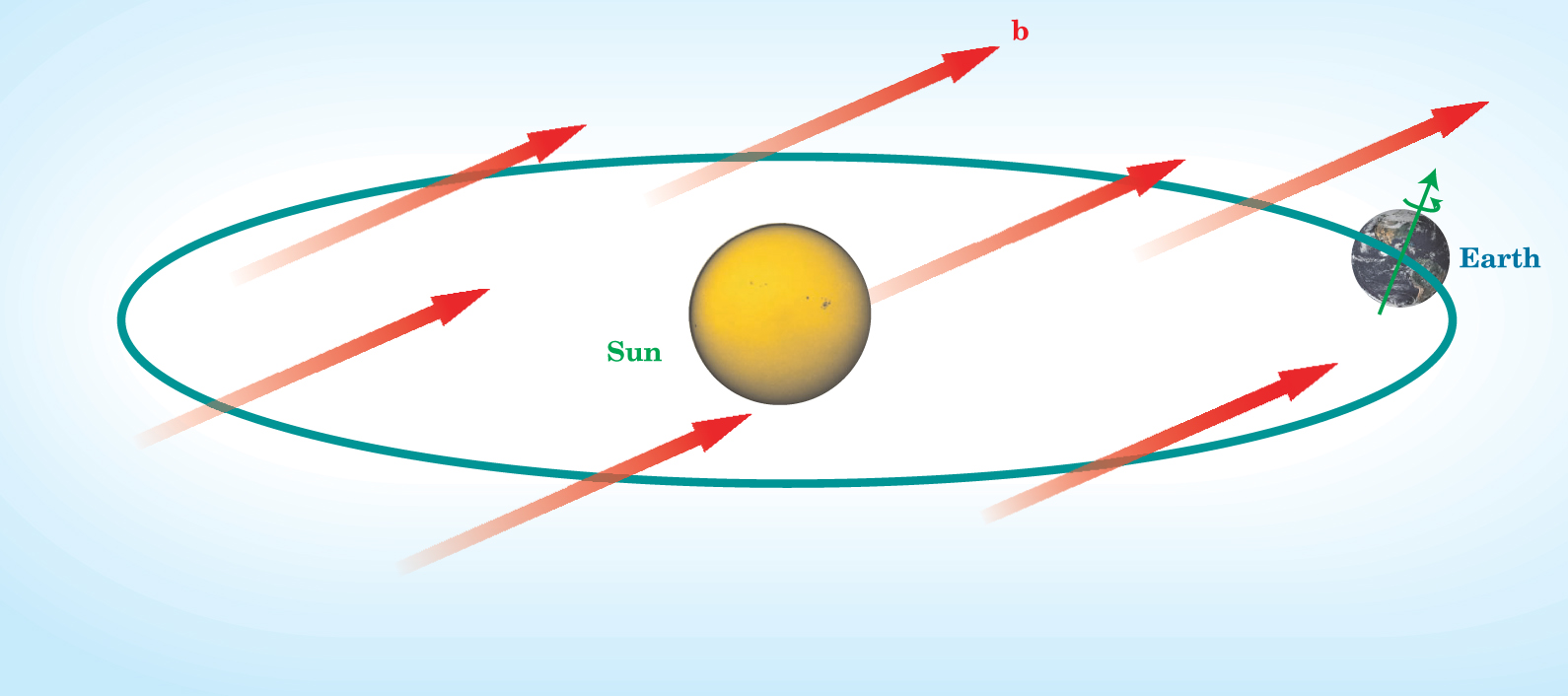
How can one break Lorentz invariance in a controllable way? The least radical approach would be to assume that low-energy physics can be described by the Lorentz-invariant dynamics of the standard model plus a number of possible background fields. Those fields, taken to be constant or slowly varying, are vectors or tensors under Lorentz transformations and are coupled to ordinary particles in such a way that the whole Lagrangian remains invariant. In that framework, called an effective field theory, the violation of Lorentz invariance is caused by nontrivial background fields such as the field illustrated in figure 1. The Lorentz violation therefore also appears as a spontaneous symmetry breaking.

Figure 1. A uniform background vector b defines a preferred direction in space and so violates Lorentz invariance. In effective field theories like those discussed in the text, b is related to the three-vector part of a four-vector.
One can classify all possible interaction operators by looking at their dimensions. In the natural units
Effective-field-theory expansions have been widely applied in particle physics since Enrico Fermi, in 1933, parameterized the then-unknown Lagrangian of weak interactions by local operators. Effective theories can preserve all of a field theory’s desirable features, including micro-causality, unitarity, gauge invariance, renormalizability, spin statistics, and energy–momentum conservation. The effective theory approach to Lorentz violation was advocated by Alan Kostelecky (Indiana University) and coworkers,
3
who developed a systematic generalization of other theoretical descriptions of Lorentz-violating effects.
4–6
Applying the effective-field-theory approach to quantum electrodynamics, one finds that the lowest relevant operator dimension is three and that the QED Lagrangian may be expressed in terms of three dimension-three interactions:
One can extend the QED Lagrangian by adding other standard-model fields or higher-dimension interactions. Operators of dimension five and higher can lead to significant modifications of the dispersion relations for particles at high energies. 7
The effective-field-theory language allows scientists to systematically study violations of Lorentz invariance. They can assign to experiments a figure of merit that depends on the experimental sensitivity to the Lorentz-violating effects. The effective-field-theory framework also provides general guidance as to the types of effects one would observe. Among those effects are rotational dependences of spin-precession frequencies or of the speed of light (such effects can be measured in low-energy experiments),
Comagnetometers
Modern descendants of Hughes–Drever experiments provide very stringent constraints on many possible Lorentz-violating parameters. Consider the fermionic part (that is, the first two terms) of the Lagrangian given in equation
In this equation, b is a vector with components
The precession frequency depends on the magnetic field, which generally is much greater than a possible b term. Thus, one must exclude drifts of the magnetic field as a possible source of frequency change. Typically, that’s done with experiments that compare two frequencies proportional to the same magnetic field—either the spin precession frequencies of two different species or the spin and orbital precession frequencies of the same species. Because Lorentz-violating operators coupled to the spin cause only small additive energy shifts, experimentalists generally try to keep the precession frequency small to maximize the fractional shift in the frequency. The
Most experiments use a magnetic field fixed on Earth. They rely on Earth’s rotation to change the direction of the field relative to the preferred frame defined by b and to produce a diurnal modulation of the precession frequency. But such a modulation is only sensitive to the components of b perpendicular to Earth’s rotation axis. An experiment on a rotating platform or in orbit around Earth allows one to constrain other components of
Hughes–Drever experiments performed in recent years have probed a variety of systems, including singly charged positive beryllium ions, atom pairs such as mercury-199 and mercury-201 or 3He and 21Ne, proton–antiproton or electron–positron pairs in a Penning trap, and muons in a storage ring. With the help of simple atomic and nuclear models, experimenters can interpret their measurements in terms of limits on the Lorentz-violating interactions for the electron (b e), neutron (b n), and proton (b p). One needs a concrete model for the origin of Lorentz violation, though, to predict the strength of the backgroundfield couplings to different elementary particles.
Comagnetometer Measurements
To understand more precisely the Lorentz-violating effects in comagnetometer experiments, which compare the precession of two particles, consider two nuclei with magnetic moments µ1 and µ2. Assume that they couple to the same Lorentz-violating field b but with different coupling coefficients β1 and β2. The precession frequencies of the two nuclei are given by
Thus, in comagnetometer measurements, one can detect a Lorentz-violating field only to the extent that it does not couple to particle spins in proportion to the particles’ magnetic moments.
Precision measurements of such nonmagnetic spin interactions have been used over the years—for example, in searches for a permanent electric dipole moment or for spin-dependent forces mediated by a proposed particle called the axion. In single species experiments, one concern is the influence of Lorentz-violating effects in commonly used magnetic shielding; comagnetometer measurements, in contrast, are not sensitive to those effects.
Laboratory bounds
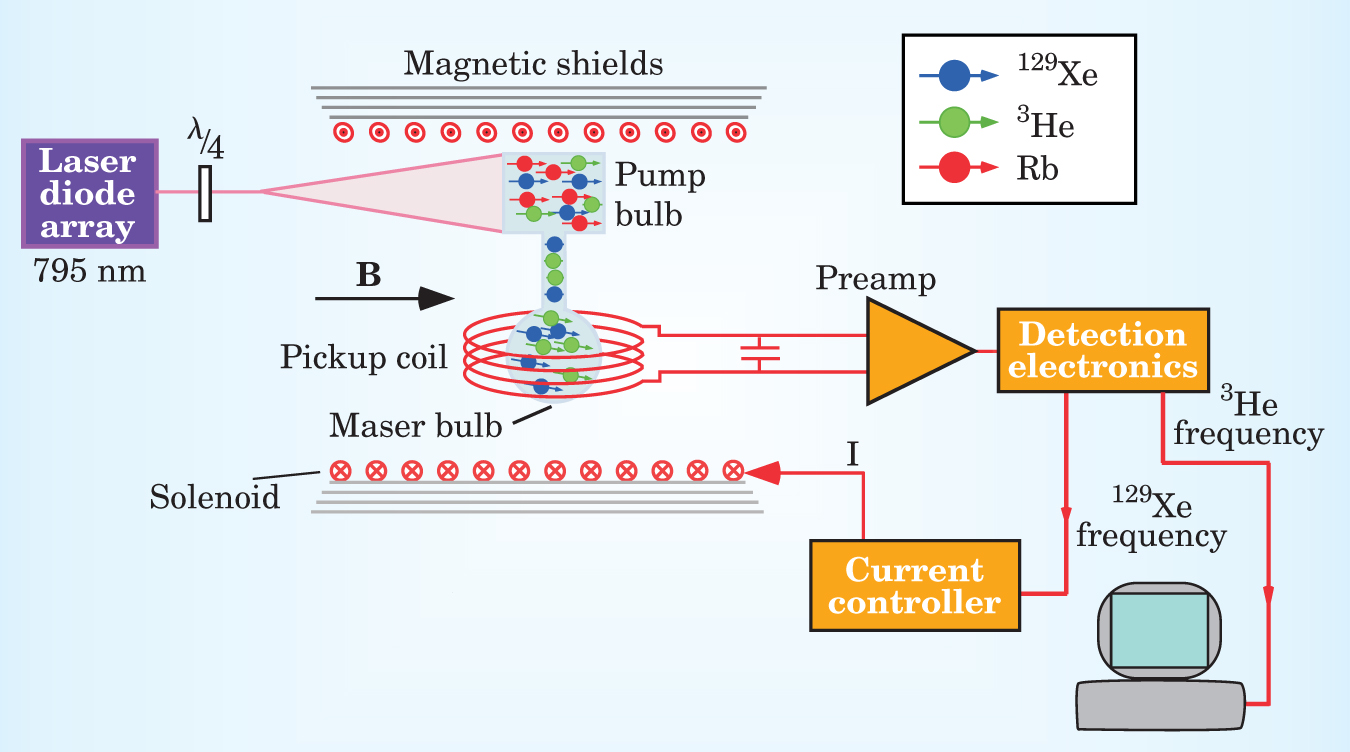
The best limit on the Lorentz-violating b n term—indeed, the highest overall energy sensitivity to Lorentz-violating frequency shifts—has been obtained in a 3He–129Xe maser developed at the Harvard–Smithsonian Center for Astrophysics (CfA). 8 Figure 2 illustrates a schematic of the experiment. The free spin precession frequencies of the 3He and 129Xe are simultaneously measured by maintaining persistent Zeeman maser oscillations for both species. The two atoms operate as a comagnetometer because, absent Lorentz violations, their precession frequencies are proportional to the same magnetic field. The frequency of the 129Xe maser is held constant with the help of a magnetic field adjusted via feedback. Any change in the 3He frequency with time would thus indicate an anomalous coupling to the nuclear spins.

Figure 2. A spin maser experiment with helium-3 and xenon-129 atoms sets the best limit on Lorentz-violating effects for the neutron. A double-bulb glass cell contains 3He and 129Xe atoms in both chambers and additional rubidium atoms in the upper bulb. An optical pumping laser array spin-polarizes the Rb atoms, which transfer their polarization to the 3He and 129Xe via spin-exchange collisions. The lower bulb is located inside a pickup coil connected to an external resonator with resonances at the Zeeman frequencies for both 3He and 129Xe. Resonance currents in the pickup coil maintain a persistent precessing magnetization of both spin species while the current controller adjusts the magnetic field to maintain a constant spin-precession frequency for the 129Xe. Any change in the 3He spin-precession frequency thus indicates a Lorentz-violating spin interaction.
(Figure courtesy of Ron Walsworth, Harvard–Smithsonian Center for Astrophysics.)
In a simple nuclear shell model, both 3He and 129Xe have a single valence neutron, and thus their coupling coefficients, as defined in the box, are equal. But their magnetic moments differ by a factor of 2.75, and so one retains sensitivity to the neutron Lorentz-violating term. After approximately 90 days of integration, the CfA experiment observed, with an uncertainty of 45 nHz, no modulation of the 3He precession frequency at Earth’s rotation rate. Such precision means that the part of b n perpendicular to Earth’s rotation axis has a magnitude less than 5 × 10−32 GeV. That incredible sensitivity underlines how such bounds can constrain models of new physics.
The best limit on Lorentz violation for electrons comes from a torsion pendulum experiment developed by the Eöt–Wash group at the University of Washington. It uses a toroidal pendulum consisting of two different kinds of permanent magnets, an aluminum-nickel-cobalt-iron (Alnico) alloy whose magnetization is mostly produced by electron spin alignment, and a samarium–cobalt magnet whose magnetization has a significant contribution from the orbital angular momentum of the Sm electrons. By adjusting the magnetization of the Alnico magnets, the Eöt–Wash experimenters can balance the magnetization in the toroidal ring and almost perfectly cancel the net magnetic moment of the pendulum. However, because part of the contribution to the magnetization comes from orbital angular momentum, the pendulum still has a large unbalanced electron spin.
The pendulum hangs from a fiber and rests inside a set of magnetic shields. The whole apparatus sits on a precision turntable surrounded by Helmholtz coils and suitably positioned masses that reduce magnetic and gravitational field gradients. Any Lorentz-violating spin coupling would cause a torque on the pendulum; that torque would oscillate at the approximately 1-hour rotation period of the turntable. A laser beam reflected from a mirror mounted on the pendulum allows the Eöt–Wash researchers to measure the pendulum’s rotation with a sensitivity of 4 nanoradians.
The pendulum experiment set limits on the b e components of less than 2 × 10−29 GeV. Note that the turntable-mounted experiment constrains the component of b e parallel to Earth’s rotation axis. A similar experiment, recently completed at Tsing Hua University in Taiwan, has achieved comparable sensitivity to that of the Eöt–Wash group. 9
Effective field theories can also include interactions that allow Lorentz violation in the photon sector: The last term of equation
Modern descendants of the Michelson–Morley experiment furnish the best limits on light-speed anisotropies. Stimulated by renewed interest in tests of Lorentz invariance, groups at Stanford University, Humboldt University in Berlin, Germany, and the Observatoire de Paris have recently completed such experiments, in which one measures the resonance frequency of an optical or microwave cavity cooled to liquid He temperatures. As Earth rotates, the orientation of the cavity changes relative to a fixed reference frame. If the velocity of light were to depend on direction, the changing orientation would cause a shift in the resonance frequency. The most sensitive present limits have been set by the Humboldt group, which compared the resonant frequencies of two optical cavities made from crystalline sapphire that were oriented at 90° to each other.
10
They collected data for about a year and established a limit for variations in the speed of light of
The next generation of experiments is already being developed. The CfA group is presently working to improve the long-term stability of their 3He–129Xe maser. They are also working on improving a hydrogen maser experiment that has set the best limit on the Lorentz-violating proton interactions. A group at Amherst College is improving a 1995 Hughes–Drever-type experiment
11
that compared the spin precession of mercury-199 and cesium-133 atoms and achieved a high short-term sensitivity: Their new experiment will sit on a magnetically shielded rotary table. The Eöt–Wash group is also implementing significant improvements, including an active tilt-stabilization system for their turntable and a pendulum with a higher spin moment. A new experiment being developed at Princeton University will use potassium and 3He atoms that together operate as a self-compensating atomic comagnetometer
12
that is sensitive to a particular combination of neutron and electron violating coefficients,

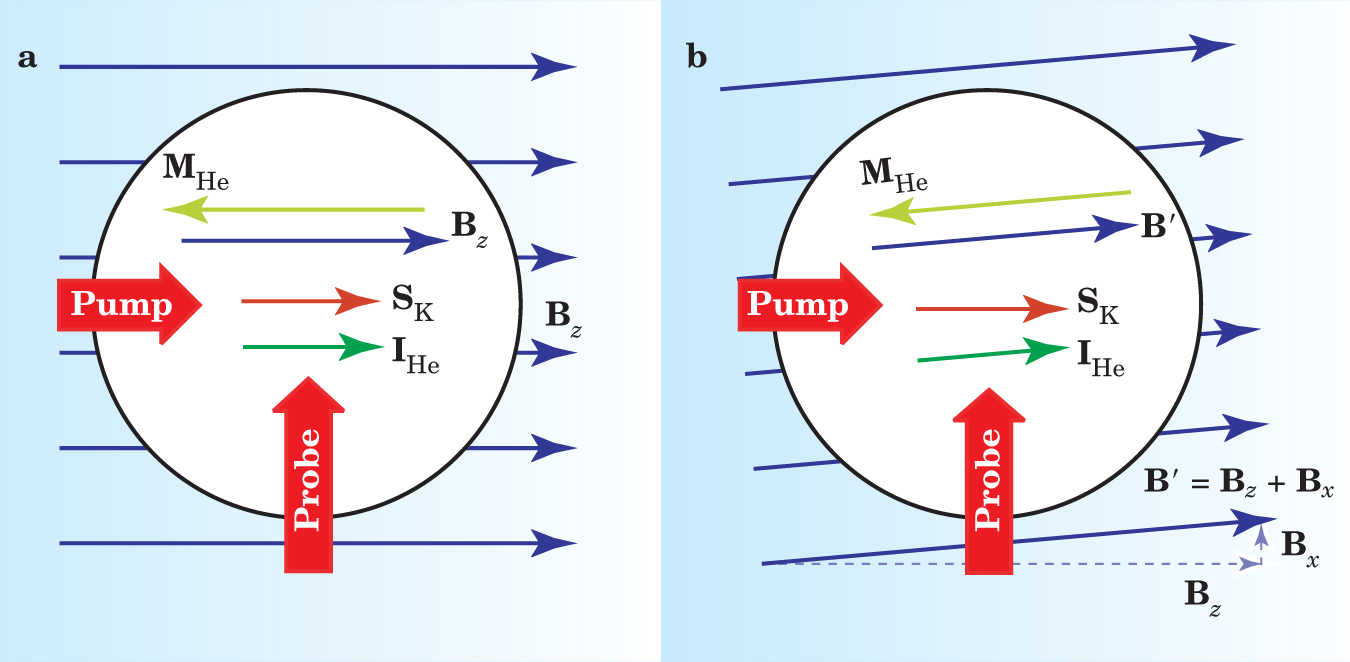
Figure 3. A new experiment being developed at Princeton University uses a self-compensating potassium–helium-3 comagnetometer. (a) Optical pumping polarizes K atoms, which transfer some of their polarization S K to 3He through spin-exchange collisions. The 3He, whose nucleus has spin I He, develops a significant magnetization M He directed opposite to the applied longitudinal magnetic field B
(Figure courtesy of Tom Kornack, Princeton University.)
The experiments now being developed should improve existing limits by about two orders of magnitude. One challenge faced in experiments designed to look for Lorentz violations is that the slow frequency of signal modulation makes them very susceptible to 1/
CPT
Particle physicists have a long history of testing
The most stringent constraints on
Lorentz-symmetry and
The coupling of the
Astrophysical and cosmological tests
Astronomical observations can place extremely tight constraints on certain types of Lorentz violation, such as changes in the polarization of light propagating through space. A rotation in linear polarization is implied, for example, by the last term of equation
Other Lorentz-violating terms cause polarization rotations that depend on wavelength. They can be measured by observing visible polarized light emitted by distant galaxies. Scattering from dust or electrons is typically responsible for polarizing the light, and so the initial polarization is independent of wavelength. By measuring the polarization of scattered light over a range of wavelengths, one can set a limit on wavelength-dependent rotation due to Lorentz-violating effects. 13
Another manifestation of Lorentz violation, which can arise when higher-dimension interactions are included in an effective theory, is a modification of the usual dispersion relation
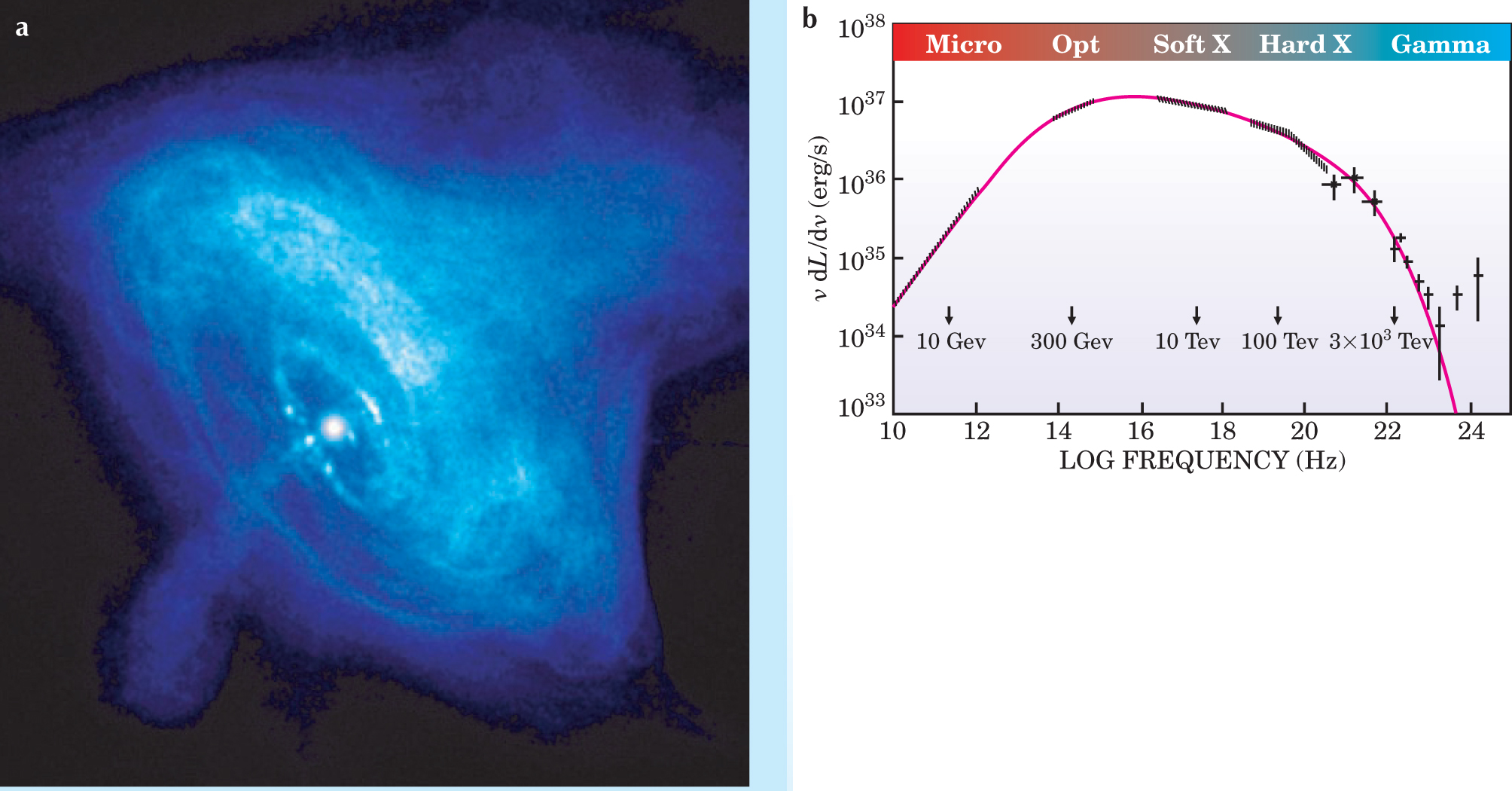
Observed very high-energy astrophysical processes have significantly constrained possible modifications to the standard dispersion relation. For example, synchrotron radiation from the Crab Nebula (figure 4) has been observed with energies of up to 100 MeV, and several methods estimate the nebula’s magnetic field to be in the range of 20–50 nanotesla. Together, those two values imply that electrons are accelerated up to energies of at least 1500 TeV, corresponding to velocities that differ from the speed of light by less than one part in 1019. The electrons accelerated to such energies must be stable against the vacuum Čerenkov radiation process

Figure 4. (a) X rays in the Crab Nebula are the synchrotron radiation of electrons accelerated in the shock waves created by the supernova explosion of 1054 AD. This image was taken by the
(Panel b adapted from A. M. Atoyan, F. A. Aharonian, Mon. Not. R. Astron. Soc. 278, 525, 1996.)
Challenges for quantum gravity
The Planck mass
For modified dispersion relations arising from dimension-5 operators, left- and right-handed fermions may both be described by the three displayed terms in equation
Astrophysical observations, such as those from the Crab Nebula, constrain various combinations of the electron’s and photon’s ξ and η parameters with unprecedented accuracy,
15
sometimes to better than 10−7. Perhaps more surprising is that spin precession experiments also provide comparable constraints.
7
If one assumes the dispersion relationships are written in the cosmic microwave background rest frame, then any difference between η
An important and different kind of small-length-scale physics that leads to the violation of Lorentz invariance is a feature of noncommutative field theories. In such theories, which naturally arise in the context of certain string theories,
16
spacetime coordinates are noncommuting operators:
An antisymmetric tensor, θµν has the same Lorentz transformation properties as the electromagnetic field tensor, and so it may be no surprise that its “magnetic” component
Considerations of modified dispersion relations and noncommutative field theories underline the importance of continued experiments designed to detect Lorentz invariance. In both examples, the scale of the high-energy physics responsible for Lorentz breaking can be probed with unprecedented reach.
Cosmological models
Our discussion thus far has been in the framework of special relativity, for which constant Lorentz-violating backgrounds can be justified. In general relativity, such constant fields necessarily become a function of coordinates: Backgrounds such as
A possible candidate for dark energy that avoids some of the fine-tuning problems associated with the cosmological constant is quintessence, a very low-energy field with a wavelength comparable to the size of the observable universe. In addition to its effect on the expansion of the universe, quintessence might also manifest itself through its possible interactions with matter and radiation. 2,18
One would expect that a quintessence field ϕ related to dark energy would still be evolving and that its continuing evolution in time and space would lead to Lorentz-violating effects. As an example, consider the simplest form of scalar and pseudoscalar (that is, containing γ5) couplings between a massive Dirac fermion—say, an electron or quark—and the scalar quintessence field ϕ. The Lagrangian
The time and space derivatives of ± should be somewhat smaller than the square root of the present energy density in the universe. Assuming that the spatial derivative ∇ϕ has a magnitude on the order of (0.01 eV)2, Hughes–Drever experiments imply that the pseudoscalar (
If future searches for Lorentz invariance and time-dependent fundamental “constants” bring positive results, they may prove that the universe contains a long-wavelength degree of freedom and point toward the nature of quintessence. Then the variation of fundamental constants and apparently Lorentz-violating spin precessions might be completely demystified: They could both follow from the conventional physics of an interacting scalar field.
References
1. V. W. Hughes, H. G. Robinson, V. Beltran-Lopez,Phys. Rev. Lett. 4, 342 (1960); R. W. P. Drever, Phil. Mag. 5, 409 (1960).
2. C. M. Will, Theory and Experiment in Gravitational Physics, Cambridge U. Press, New York (1993).https://doi.org/10.1017/CBO9780511564246
3. See, for example, D. Colladay, V. A. Kostelecky,Phys. Rev. D 55, 6760 (1997); Phys. Rev. D 58, 116002 (1998);https://doi.org/10.1103/PhysRevD.55.6760
V. A. Kostelecky, C. D. Lane, Phys. Rev. D 60, 116010 (1999).https://doi.org/10.1103/PhysRevD.60.1160104. S. R. Coleman, S. L. Glashow, Phys. Rev. D 59, 116008 (1999).https://doi.org/10.1103/PhysRevD.59.116008
5. S. M. Carroll, G. B. Field, R. Jackiw, Phys. Rev. D 41, 1231 (1990).https://doi.org/10.1103/PhysRevD.41.1231
6. P. J. Peebles, R. H. Dicke, Phys. Rev. 127, 629 (1962);https://doi.org/10.1103/PhysRev.127.629
K. J. Nordtvedt, Astrophys. J. 161, 1059 (1970);https://doi.org/10.1086/150607
A. P. Lightman, D. L. Lee, Phys. Rev. D 8, 364 (1973);https://doi.org/10.1103/PhysRevD.8.364
W.-T. Ni, Phys. Rev. Lett. 38, 301 (1977).https://doi.org/10.1103/PhysRevLett.38.3017. D. Sudarsky, L. Urrutia, H. Vucetich, Phys. Rev. Lett. 89, 231301 (2002);https://doi.org/10.1103/PhysRevLett.89.231301
R. C. Myers, M. Pospelov, Phys. Rev. Lett. 90, 211601 (2003).https://doi.org/10.1103/PhysRevLett.90.2116018. D. Bear et al., Phys. Rev. Lett. 85, 5038 (2000);https://doi.org/10.1103/PhysRevLett.85.5038
Erratum: Phys. Rev. Lett. 89, 209902–E (2002).9. B. R. Heckel et al., (Eöt–Wash group), in CPT and Lorentz Symmetry II, V. A. Kostelecky, ed., World Scientific, River Edge, NJ (2002);
R. Bluhm, V. A. Kostelecky, Phys. Rev. Lett. 84, 1381 (2000);https://doi.org/10.1103/PhysRevLett.84.1381
L.-S. Hou, W.-T. Ni, Y.-C. M. Li, Phys. Rev. Lett. 90, 201101 (2003).https://doi.org/10.1103/PhysRevLett.90.20110110. H. Müller et al., Phys. Rev. Lett. 91, 020401 (2003).https://doi.org/10.1103/PhysRevLett.91.020401
11. C. J. Berglund et al., Phys. Rev. Lett. 75, 1879 (1995).https://doi.org/10.1103/PhysRevLett.75.1879
12. T. W. Kornack, M. V. Romalis, Phys. Rev. Lett. 89, 253002 (2002).https://doi.org/10.1103/PhysRevLett.89.253002
13. V. A. Kostelecky, M. Mewes, Phys Rev. Lett. 87, 251304 (2001).https://doi.org/10.1103/PhysRevLett.87.251304
14. G. Amelino-Camelia et al., Nature 393, 763 (1998).https://doi.org/10.1038/31647
15. T. Jacobson, S. Liberati, D. Mattingly, Nature 424, 1019 (2003).https://doi.org/10.1038/nature01882
16. N. Seiberg, E. Witten, J. High Energy Phys. 1999(09), 032 (1999);https://doi.org/10.1088/1126-6708/1999/09/032
M. R. Douglas, N. A. Nekrasov, Rev. Mod. Phys. 73, 977 (2001).https://doi.org/10.1103/RevModPhys.73.97717. I. Mocioiu, M. Pospelov, R. Roiban, Phys. Lett. B 489, 390 (2000).https://doi.org/10.1016/S0370-2693(00)00928-X
18. S. M. Carroll, Phys. Rev. Lett. 81, 3067 (1998).https://doi.org/10.1103/PhysRevLett.81.3067
More about the authors
Maxim Pospelov
Maxim Pospelov, 1 University of Victoria, British Columbia, US .
Michael Romalis, 2 Princeton University, New Jersey US .




