Living cells on the move

Much like birds fly in flocks and fish swim in schools, cells in our body move in groups. Collective cell migration enables embryos to develop, wounds to heal, and cancer cells to invade healthy tissue. Such phenomena involve complex biochemical regulation, but their dynamics can be predicted by the emerging physical principles of living matter. (For more about biochemical regulation in cells, see the article by Christoph Zechner and Christoph Weber on page 38 of this issue.)

At the microscale, our body is a busy maze filled with moving cells. Their movements are slow, rarely exceeding 10 µm/min, but they are crucial to immune response and tissue self-renewal. Through the same mechanisms that sustain these and other physiological functions, cell movements drive devastating diseases such as acute inflammation and cancer. Indeed, they can be considered diseases of cell movement because arresting the right cells in a controlled manner would be sufficient to prevent their spread. Take cancer as an example. Whereas its origin is well known to be genetic, we could prevent tumor cells from metastasizing in distant organs if we could halt their movement. Understanding cell migration is therefore crucial to improving current strategies for fighting disease.

Cell migration comes in different flavors. Some cell types move as isolated self-propelled particles. For example, to chase and destroy pathogens, immune cells move individually through tissue pores. Similarly, in some types of cancer, single cells dissociate from tumors and travel through surrounding tissue, eventually reaching blood vessels and metastasizing at distant organs. By contrast, in embryo development, cells move in groups to enable the precise positioning of tissues and organ progenitors. Well after birth, those movements continue to shape organs and drive wound healing. In tissues such as the skin, a continuous sheet of tightly adhered cells moves cohesively over any damaged area to heal it.

Likewise, cancer cells migrate in the form of cell sheets, strands, and clusters, as shown in figure 1a. Within those groups, cells organize themselves to behave like an aberrant organ. This added functionality is thought to provide malignant tumors with distinct strategies to improve their chances of spreading into surrounding tissues.

Figure 1.

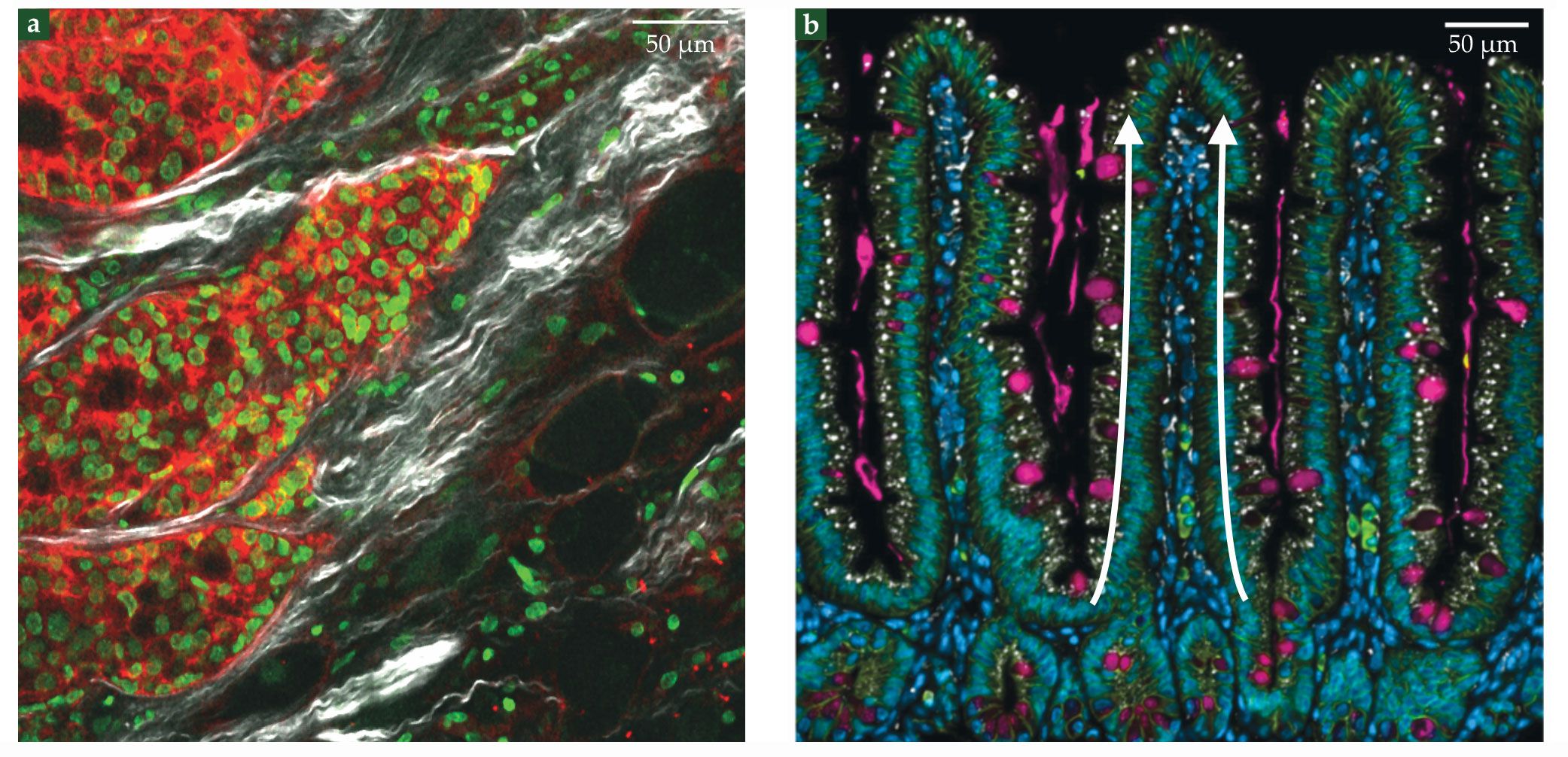
Collective migration is also involved in maintaining the inner surface of the gut—the fastest self-renewing tissue in mammals. It renews entirely every three to five days, which implies a daily loss of several grams of cells. Tissue renewal proceeds because of the division of stem cells that reside at the bottom of tissue invaginations called crypts. The progeny of those stem cells then migrates from the crypt to the top of fingerlike protrusions called villi, where they are shed into the fluid-filled interior of the intestine (see figure 1b) and discarded.

A myriad of molecular processes, from genetic programs to sensing and signaling pathways, regulate collective cell migration. Yet, they act on a limited number of physical quantities to determine cell movement. Therefore, coarse-grained approaches may provide crucial insight into biological questions. Furthermore, collective cell behaviors have inspired new physical theories of living systems. In this article we highlight progress on that front.

Cell assemblies as living matter

What physical principles underlie collective cell motion? In traditional condensed matter, interactions between electrons or atomic nuclei give rise to fascinating collective phenomena such as magnetism and superconductivity. In an analogous way, cell–cell interactions can also lead to emergent collective phenomena in migrating cell groups. When treating cell colonies as materials, however, we must take into account some key features of living matter.

First, the primary constituents of living tissues are cells and extracellular networks of protein fibers, such as collagen. The interactions between these mesoscale constituents are orders of magnitude weaker than interatomic interactions in conventional solids. With notable exceptions, such as bone, most biological tissues are soft materials, which can easily deform and flow.

Second, cells are machines with internal engines. Specialized proteins known as molecular motors harness the energy of chemical reactions to generate forces and produce mechanical work. These energy-transducing molecular processes ultimately power cell migration and allow cells to move autonomously without externally applied forces. The continuous supply of energy drives living tissues out of thermodynamic equilibrium. Importantly, the driving is local; it occurs at the level of single cells. In other words, cells are active constituents, and living tissues are a paradigmatic example of active matter—an exploding new field in nonequilibrium statistical physics.

Cells are not only mechanically active; they also sense their environment, process information, and respond by adapting their behavior. For example, stem cells plated on substrates of different stiffness differentiate into distinct cell types—from brain cells to bone cells. Living tissues are adaptive; they respond in programmed ways to environmental cues, such as external forces, mechanical properties of the extracellular matrix, and concentrations of nutrients and signaling molecules.

Consequently, cell–cell and cell–environment interactions are often quite complex. Unlike atoms and electrons in conventional condensed matter, cellular interactions cannot in general be fully described via an interaction potential with a fixed functional form. Thus, a key challenge in the physics of living matter is to find effective ways to capture complex cell behaviors in terms of simple interactions. ¹

To flow or not to flow

One way to think about interactions between deformable epithelial cells comes from the physics of foams. In foams, gas bubbles arrange in polygonal packings, with the liquid phase filling the interstitial spaces and providing surface tension at bubble interfaces, shown in figure 2a. Cells in epithelial monolayers (see figure 2b) also acquire polygonal shapes, with roughly straight edges subject to active tension generated inside cells. This description of tissues as cell packings goes back to work by Hisao Honda and collaborators in 1980, and it was later popularized in work by Frank Jülicher and colleagues. ²

Figure 2.

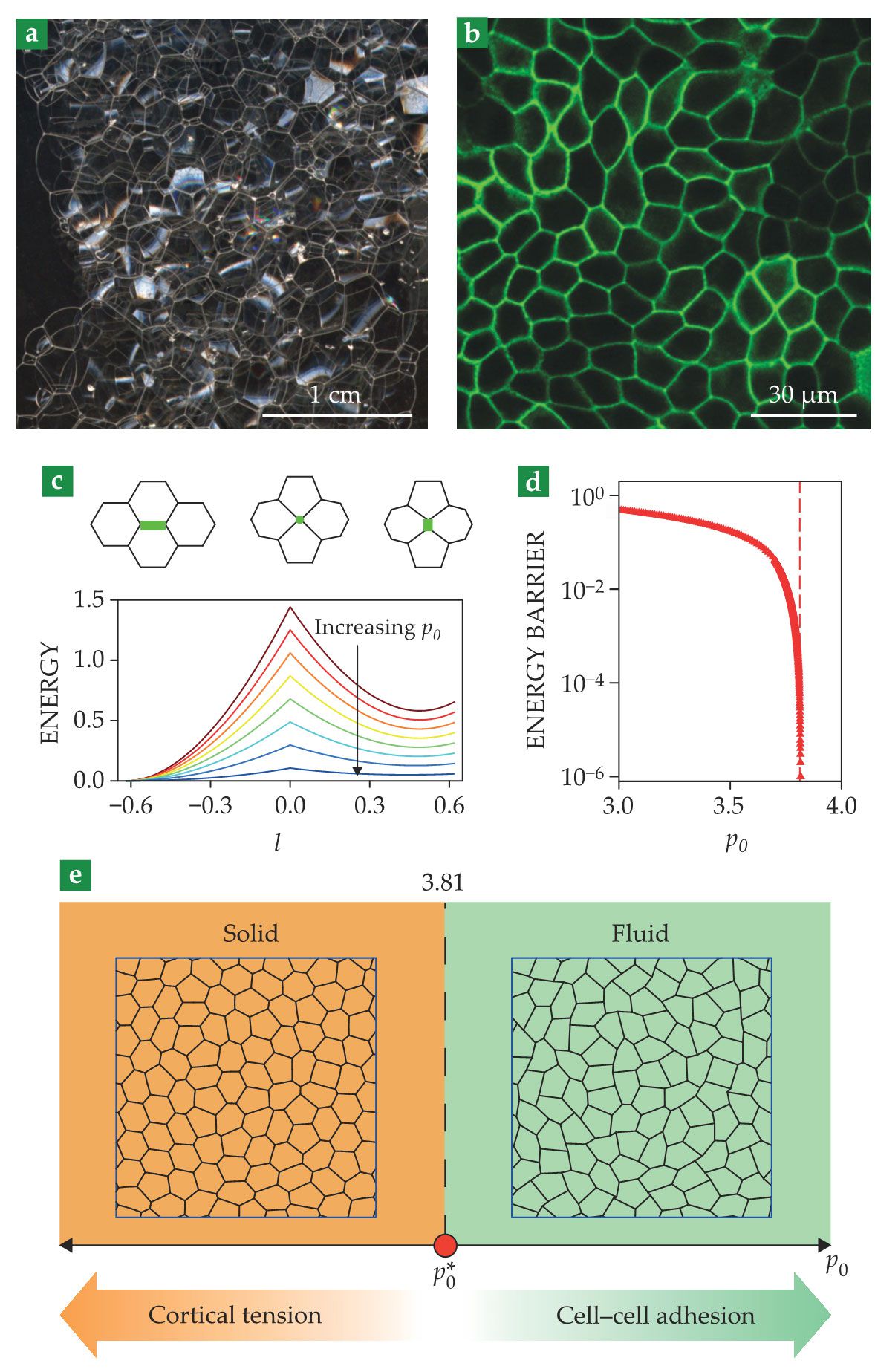
Because cells are deformable, edge lengths vary dynamically. These variations change the energy—or more formally, the Hamiltonian—of the cellular network, which one can write in terms of areas $A_i$ and perimeters $P_i$ of $N$ cells, as $$H=\sum _{i=1}^N[\frac{\kappa }{2}{(A_i-A_0)}^2+\frac{\Gamma }{2}{(P_i-P_0)}^2]\text{.}$$ This expression assumes that cells resist changes in their area and perimeter around the preferred values of $A_0$ and $P_0$, with elastic moduli $\kappa$ and $\Gamma$ respectively. The preferred perimeter $P_0$ depends on cell–cell interactions and cellular activity, with cell–cell adhesion promoting longer edges and cellular tension favoring shorter edges. The preferred perimeter and preferred area define a dimensionless parameter $p_0=P_0/\sqrt{A_0}$, which contains information about the preferred cell shape. Higher $p_0$ corresponds to more elongated cells, whereas smaller $p_0$ corresponds to more isotropic shapes—with less perimeter for the same area.

For a given $p_0$, edge lengths vary until the system reaches its ground state and minimizes the energy in the equation. In that process, an edge can shrink until it eventually disappears and a new cell–cell interface forms (see figure 2c). Known as T1 transitions, those events allow cells to change neighbors and drive topological rearrangements of the cellular network.

The ability to reorganize its constituents determines whether a material is solid or fluid. If cell rearrangements are difficult, the cellular network resists shear deformations; the tissue is solid. In contrast, if cells can rearrange easily, the network yields to shear; the tissue is fluid. At small $p_0$ (that is, for rounder cells), the equation implies that an energy barrier prevents T1 rearrangements. However, as $p_0$ increases and cells become more elongated, the energy barrier decreases (see figure 2c). At a critical value of $p_0$ around 3.81, the barrier vanishes (see figure 2d) and cells can rearrange freely. ³

That simple model thus predicts a solid–fluid transition in tissues that is driven by changes in cell shape (see figure 2e). It’s a striking prediction that showcases the bizarre mechanical properties of materials with deformable constituents. In conventional condensed matter, solids can melt by increasing temperature, or they can melt by either reducing the packing fraction or, equivalently, decreasing pressure. Tissues, however, can melt at a fixed temperature and at the maximum packing fraction, without gaps between cells. ³ They can become fluid by increasing the cell perimeter-to-area ratio in one of two ways: either decreasing intracellular tension or, counterintuitively, increasing the cell–cell adhesion. The more that cells adhere to one another, the more they elongate and the easier it is for them to rearrange.

Shortly after its prediction, ³ such a solid–fluid transition was experimentally verified in layers of human bronchial epithelial cells. ⁴ The same study showed that cells from healthy individuals tended to be caged by their neighbors and form a solid tissue, whereas cells from asthmatic individuals tended to remain unjammed and form a fluid tissue. Therefore, the experiments suggested, fluid–solid transitions in tissues are involved in disease—a finding that opens the door to new treatments based on preventing those phase transitions.

Fluid–solid transitions also occur during development, which enables tissues first to turn fluidic so they can remodel and acquire their shapes and then to solidify and mature. The emerging picture is that in different biological contexts cells can tune their shape and use the physical principles governing phase transitions in foams to decide whether to flow or not to flow.

Aligning with neighbors

The action starts once tissues become fluid and cells can move. Cells then start to flow collectively in ways that depend on how they align with their neighbors. These cell–cell interactions depend strongly on cell shape.

Cells come in many different shapes, such as roughly spherical and rodlike. Some develop a head–tail asymmetry and migrate persistently in one direction, which can be represented by a vector known as cell polarity. And in groups, cells can align their individual polarities to form phases of matter with orientational order.

The alignment interactions and the resulting oriented phases can be described using concepts from magnetism and liquid crystals. For example, cells in a group can spontaneously break symmetry and align in a common direction. To capture the emergence of this kind of alignment, known as polar order, one can introduce ferromagnetic-like interactions between individual cell polarities. At a coarse-grained level, collective cell polarity can be thought to result from an effective free energy, with a sombrero shape that is familiar from the Landau theory of phase transitions.

In other situations, cells align along one axis but have no preferred direction of motion. Known as nematic order, this type of alignment takes its name from nematic liquid crystals, which are used in LCD screens. Some of the most prominent features of liquid crystals are singular points known as topological defects, in which alignment is locally lost. You can find such defects on your own hands: Shown in figures 3a and 3b, they are the points at which your fingerprint ridges meet.

Figure 3.

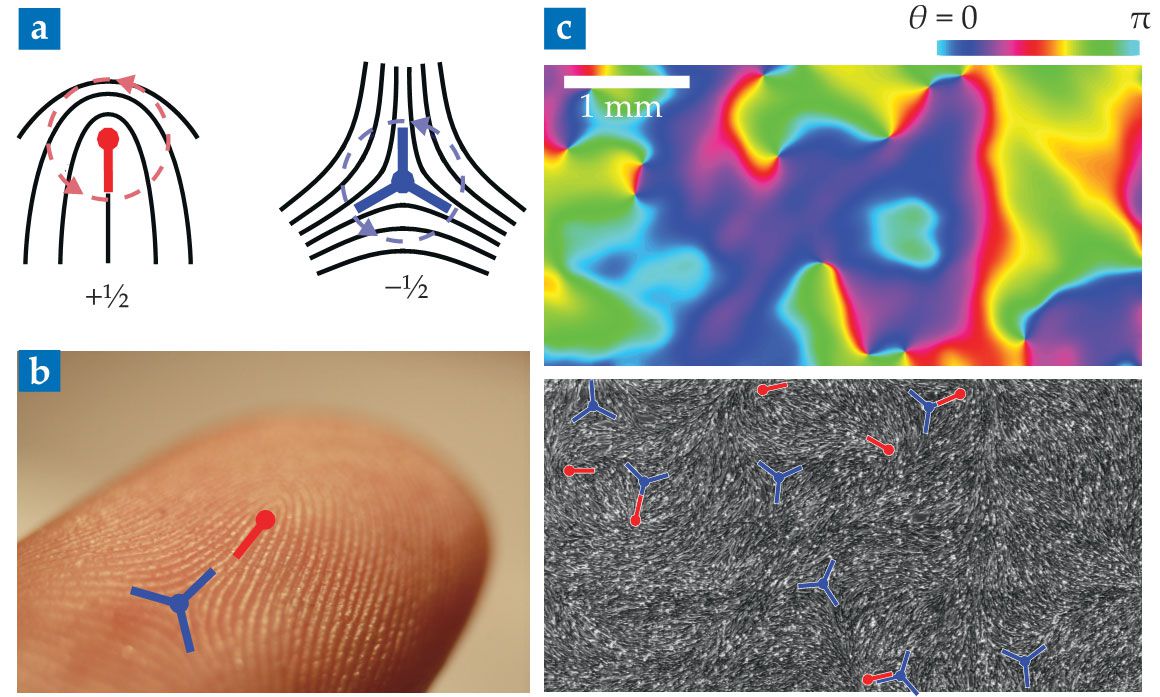
Recently, researchers have discovered topological defects in several cell assemblies, from bacterial colonies to epithelial tissues, which confirms that they can be described as liquid crystals (see figure 3c). Interestingly, topological defects can play important biological roles. For example, in epithelial monolayers, they promote cell death and extrusion ⁵ (see Physics Today, June 2017, page 19 ). In colonies of the motile soil bacterium Myxococcus xanthus, such defects promote the formation of multicellular aggregates known as fruiting bodies, which allow the bacterial population to survive starvation. ⁶

Flowing on their own

Capturing orientational order is not enough to account for collective cell flows. To understand how cell alignment translates into collective motion, physicists describe cell assemblies as active matter. ^{1 , 7} For example, when cells align with polar order, they can start migrating in the direction of alignment. ⁸ Such collective motion is known as flocking. The active-matter theory of the phenomenon, inspired by the mesmerizing flights of bird flocks, was developed more than 25 years ago. ⁹ Today, the principles of flocking are applied to many other systems—from synthetic active colloids to bacterial swarms.

To describe nematic cell colonies, researchers use the theory of active liquid crystals, which generalizes the hydrodynamics of liquid crystals to include active (cell-generated) stresses. The theory explains, among many other phenomena, the cell flows observed around topological defects. It also successfully describes many other active systems—from biopolymer gels to shaken granular materials. Employing general theories of active matter to characterize cell migration is particularly useful because it reveals connections to apparently unrelated systems. This approach is allowing the community to classify active systems based on their symmetries, in the spirit of universality classes in statistical mechanics.

For example, the theory of active liquid crystals was originally inspired by the complex autonomous flows found in bacterial suspensions and in the cell cytoskeleton. Soon after formulating the theory, researchers predicted that internal active stresses would generate an instability whereby the fluids start flowing spontaneously, without any external forces applied. ¹⁰ To drive flows, active stresses have to overcome alignment forces in the liquid crystal, which happens only at sufficiently large spatial scales. Consequently, the theory predicted that a strip of active fluid would flow only if it was wide enough. ¹⁰

More than a decade later, those predictions were tested in cell monolayers. ¹¹ Whereas cells confined in narrow stripes did not flow, cells confined in stripes wider than a critical width developed a collective shear flow, as predicted by the theory. In large tissues, cell flows become chaotic and create disordered patterns of swirls known as active turbulence. ¹² Confinement can therefore organize these chaotic cell flows, either taming them into simple shear flow or preventing them altogether.

The regulatory role of confinement may be relevant in embryonic development and tumor invasion, in which cell groups often migrate in tracks defined by surrounding tissue (see figure 1a). Overall, recent work reveals how cells can leverage the physics of active fluids to produce collective flow patterns, and how confinement controls whether and how cell groups flow on their own.

To spread or not to spread

What happens if the confinement is released and a cell monolayer is exposed to free space? Cells at the edge of the monolayer can sense that they have neighboring cells on one side but not the other. In ways that are not yet clear, edge cells respond to this asymmetric environment by polarizing toward free space, as shown in figure 4a. Specifically, the cells extend protrusions known as lamellipodia, with which they exert directed and persistent traction forces on the underlying substrate to migrate toward open ground.

Figure 4.

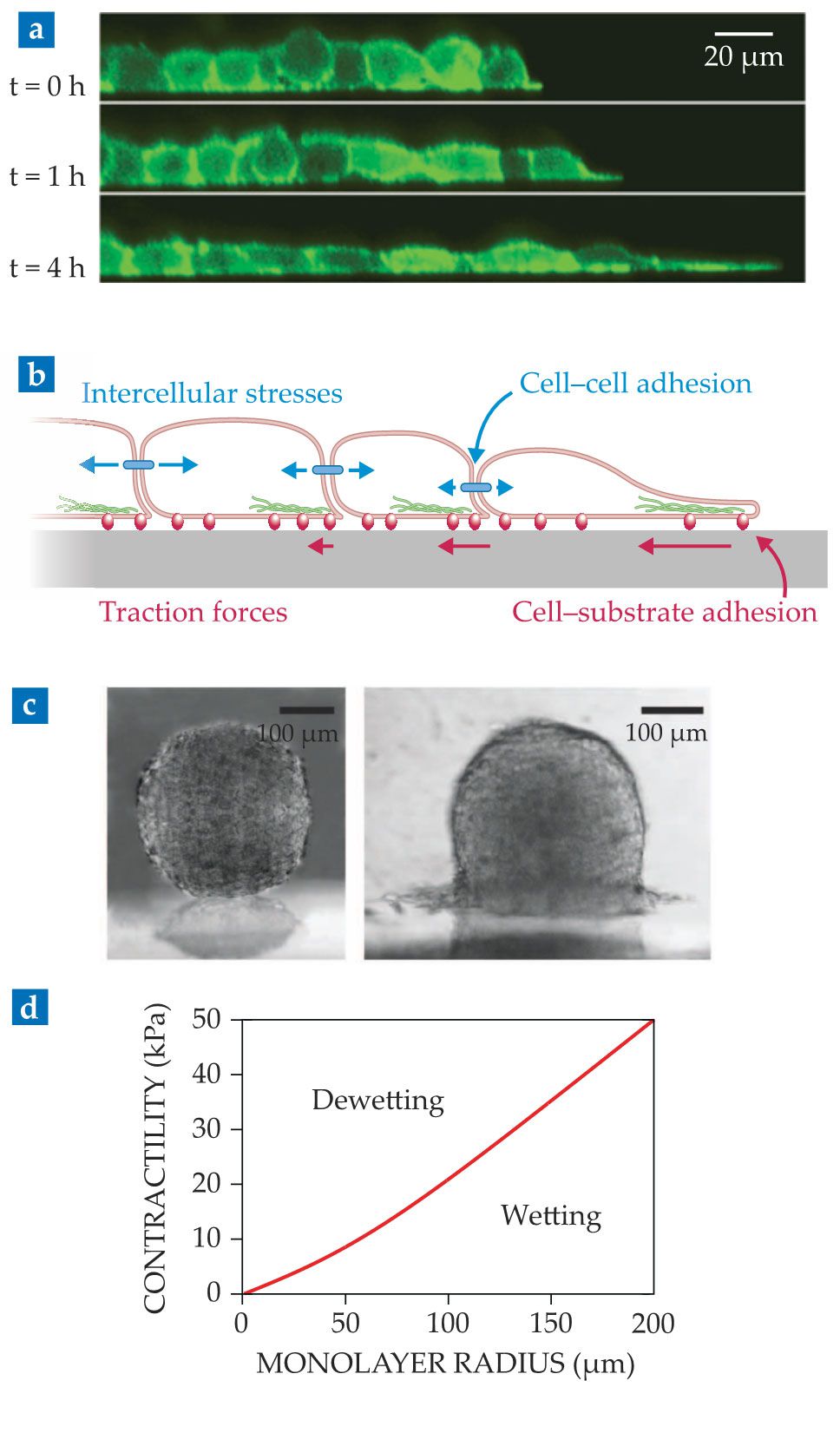
Because cells in the monolayer adhere to each other, the migrating edge cells pull on those in the second row, which then also polarize, migrate, and pull on inner cells (see figure 4b), thus setting the monolayer under tension. ¹³ At the molecular level, this supracellular coordination is mediated by a protein known as merlin, which transduces intercellular forces into cell polarization. In such a mechanically coordinated way, the entire cell monolayer spreads on the substrate and becomes progressively thinner. ¹⁴ Combined with other mechanisms, such collective cell migration helps, as in wound healing, to close the gaps in epithelial tissues.

But tissues are not always spread on substrates. Under certain conditions, a cell monolayer may instead retract from the substrate and eventually collapse into a droplet-like cell aggregate, ¹⁵ as illustrated in the opening image on page 30. Tissue spreading and retraction are reminiscent of the wetting and dewetting of liquid droplets. The degree of wetting depends on the balance between cohesive forces in the liquid and adhesive forces with the substrate.

By analogy, early models proposed that tissue wetting was dictated by a competition between cell–cell ($W_{\mathrm{cc}}$) and cell–substrate ($W_{\mathrm{cs}}$) adhesion energies, ^{16 , 17} encoded in a spreading parameter $S=W_{\mathrm{cs}}-W_{\mathrm{cc}}$. When $S$ < 0, cell–cell adhesion dominates and the cell aggregate retracts from, or dewets, the substrate, whereas when $S$ > 0, cell–substrate adhesion dominates and the aggregate spreads over, or wets, the surface (see figure 4c). This simple conceptual framework is sufficient to interpret the behavior of cell aggregates when the levels of cell–cell and cell–substrate adhesion are varied. ^{16 , 17} Even so, the analogy to passive liquids does not explicitly account for the active nature of cells.

Recent work addressed that limitation by treating the cell monolayer as a droplet of an active liquid. ¹⁵ Using this approach, one obtains the spreading parameter directly in terms of active cellular forces. Supported by experiments, the model predicts that the tissue wetting transition results from the competition between two types of active forces: Whereas cell–substrate traction forces promote spreading, cell–cell pulling forces, or tissue contractility, promote retraction.

That active wetting framework makes another key prediction: The spreading parameter depends on the droplet radius. Cell monolayers larger than a critical radius wet the substrate, whereas smaller monolayers dewet from it (see figure 4d). The prediction is striking because it has no counterpart in the classic wetting picture, in which the spreading parameter depends solely on surface tensions. For ordinary liquid droplets, size does not matter. Tissue wetting, by contrast, is size dependent. This prediction has been verified in experiments, which provide evidence for the active nature of tissue wetting. ¹⁵

Besides its relevance to physics, the existence of a critical size for tissue wetting might explain drastic changes in tissue morphology during embryonic development and cancer progression. A disturbing possibility, for example, is that a growing tumor might become able to spread onto surrounding tissue once it reaches a critical size.

Overall, the work described above exemplifies how the quest to understand collective cell migration motivates the development of new physics, as in the example of active wetting. This physics approach offers clues on how cell aggregates can tune active forces to control whether to spread or not to spread.

Mechanical waves without inertia

Tissue spreading exhibits yet another striking collective phenomenon: Mechanical waves start spontaneously at the leading edge of a cell monolayer and propagate across it, ¹⁴ as shown in figure 5. The waves are slow, with speeds between 10 µm/h and 100 µm/h and wavelengths that span several cell diameters. Like longitudinal sound waves, waves in tissues stretch and compress the cells as they travel. More strikingly, the waves are self-sustained; they can travel distances as long as 1 mm unattenuated.

Figure 5.

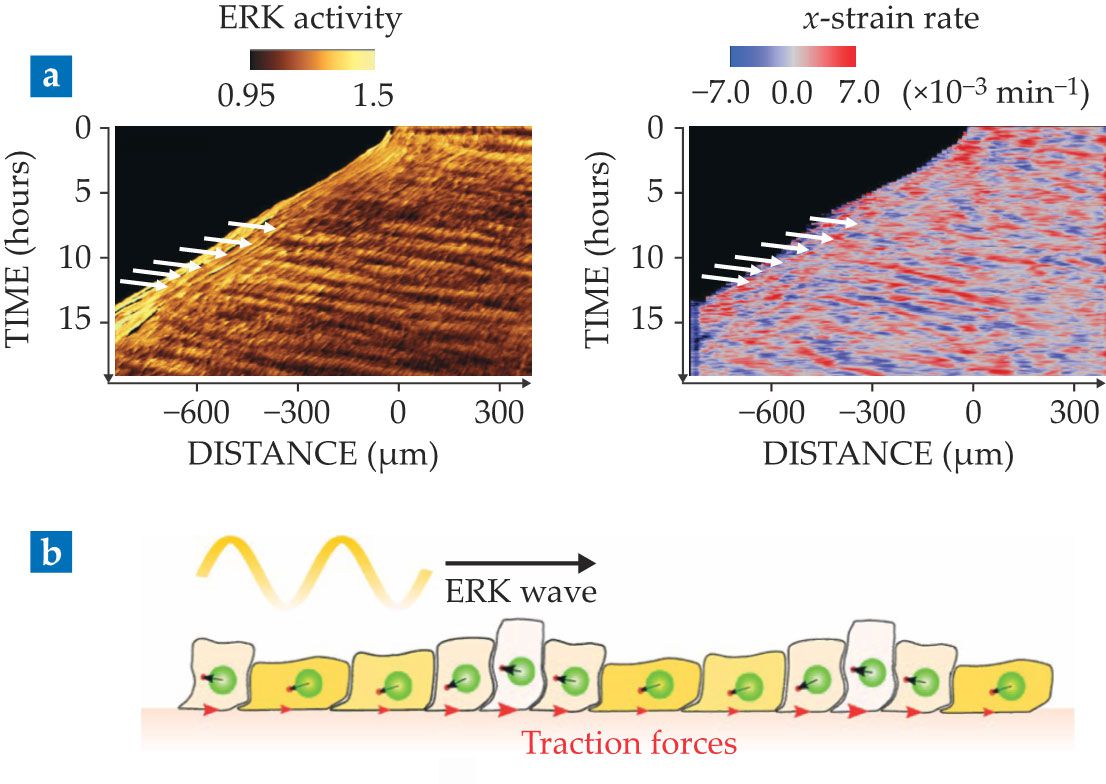
The observation is surprising because cell motion is so slow that inertia is negligible. Thus, tissue waves cannot be sustained by the common back-and-forth between kinetic and potential energies, familiar from the harmonic oscillator. Moreover, many sources of dissipation, including cell–cell and cell–substrate friction, exist in tissues and could potentially damp the waves. Thus, the very existence of mechanical waves in tissues implies an active driving mechanism that compensates damping and generates an effective inertia.

The quest to understand such waves has led to a plethora of physical models and revealed several possible mechanisms. ¹ Recently, experiments have shown (see figure 5a) that mechanical waves are accompanied by waves of ERK, an extracellular signaling molecule that affects cellular activity. Following those observations, researchers developed a theory based on the feedback between the molecule and cell mechanics, which produces coupled chemical and mechanical waves. Assuming that cells polarize in response to stress gradients in the monolayer, the theory also explains propagation away from the leading edge in spreading tissues, ¹⁸ as sketched in figure 5b.

The results show that cells can exploit mechanochemical feedbacks to transmit local information over long distances. Such tissue-scale communication is relevant for wound healing, as it enables distant cells to coordinate their migration toward the wound. Similar principles operate in morphogenesis, in that mechanochemical feedbacks enable coordinated cell deformations to precisely shape tissues without requiring local genetic control of cellular forces. The research shows that the cells’ ability to generate, sense, and respond to signals—both chemical and mechanical—can give rise to emergent phenomena as counterintuitive as mechanical waves without inertia.

The physics of active living matter is increasingly successful at explaining the dynamics of collective cell migration. This core biological process is being understood through concepts such as orientational order, flow, turbulence, jamming, wetting, and wave propagation. The mechanistic origin and physical properties of these phenomena in cells, however, differ fundamentally from those in nonliving matter. Whereas new active-matter theories manage to explain the broad phenomenology of collective cell migration in terms of a small number of physical variables, how cells tune these variables through thousands of genes and biochemical reactions remains a major open question.