Light-driven spin chemistry for quantum information science
DOI: 10.1063/PT.3.5196
Quantum information science (QIS) has many types of qubits to choose from, including superconducting and trapped-ion qubits, all with their advantages and disadvantages. Although less developed than some of the other qubit platforms, molecules and molecular systems can serve as spin-qubit arrays with distinct benefits. For example, molecular synthesis can create qubits at atomically precise locations; tailor the qubits’ magnetic, optical, and electronic properties; and construct large ordered qubit arrays through self-assembly and other strategies. 1

ISTOCK.COM/ALICE-PHOTO

Experiments from the mid 1970s showed that when light triggers electron transfer between molecules, the electrons and the electron vacancies they leave behind—known as holes—can form entangled spin states. The presence of those spin pairs is clear from time-resolved electron paramagnetic resonance (TREPR) spectroscopy, which measures the absorption or emission of gigahertz radiation as a function of an applied magnetic field—in effect, the method probes the magnetic interactions between the electron spins. Important early experiments focused on the photosynthetic-reaction-center proteins, which are responsible for the primary transduction of solar photon energy into electron–hole pairs. After photoexcitation, those proteins showed strong absorptive and emissive resonances. 2 Since then, various chemical electron donor–acceptor systems have been investigated. 3
About 10 years ago, researchers realized that photoinitiated electron–hole spin pairs can serve as spin-qubit pairs (SQPs), whose spin dynamics are of practical and fundamental interest in QIS. As with many quantum platforms, a primary challenge is generating well-defined initial states that maintain their spin coherence long enough to undergo spin manipulations and carry out quantum gate operations. 4 Those criteria are difficult to fulfill in most other materials used to create electron spin qubits because the energy gap between the spin states is so small. For example, Boltzmann statistics require millikelvin temperatures to achieve greater than 95% spin polarization. Even if one applies a 10 T magnetic field to increase the energy gap between electron spin states through the Zeeman interaction, adequate spin polarization still requires temperatures on the order of 4 K. By contrast, when electrons in molecules are excited by light, the spins resulting from electron transfer are highly polarized even at room temperature. Those molecular spin pairs can be expanded from two-spin systems to three- and four-spin systems that demonstrate desirable properties for QIS applications.
Spin-qubit pairs
Electron spins are good qubits because their two spin states constitute a prototypical two-level quantum system, in which the two states can exist in a superposition. Two or more spins can also couple through distance-dependent magnetic spin–spin exchange (with coupling constant J) and magnetic dipole–dipole interactions (with coupling constant D). Those interactions can create quantum entanglement between spins and allow for two-qubit gates essential for executing quantum algorithms. Such spin coupling occurs in many chemical systems. When a donor molecule (D) absorbs a photon, its excited electron can transfer to an acceptor molecule (A) that’s covalently linked to D by a bridge molecule (B). The resulting two spatially separated, entangled spins at D and A can function as an SQP in a well-defined pure initial quantum state. 5
Femtosecond and nanosecond transient absorption spectroscopies are typically used to characterize the ultrafast electron-transfer dynamics of D-B-A molecules. Following selective photoexcitation of D, B, or A, researchers monitor the electronic spectra of each intermediate state as a single electron transfers between subsequent component pairs. For example, if D is selectively photoexcited, an electron transfers from D to B and then from B to A, which gives intermediate states of D•+-B•−-A and D•+-B-A•−, respectively, where the superscript dot and + or − sign denote the presence of an unpaired electron spin and the net charge on D, B, and A. The spin dynamics of the SQP are then probed with TREPR spectroscopy using either continuous or pulsed microwave irradiation. The advantage of using pulsed microwaves is that one can perform specific manipulations of the spin states as a function of time that are useful for executing quantum logic gates.
The entanglement in SQPs results from spin exchange (J) and dipolar (D) couplings. The two electron spins also experience different magnetic environments because of differing electron–nuclear hyperfine couplings (a-tensors) in D•+ and A•− and differing spin–orbit interactions that lead to distinct electronic g-tensors. When the SQP is generated in a magnetic field that is much larger than all the magnetic interactions between the two spins, the SQP wavefunctions consist of a singlet state
Only the
Figure 1.
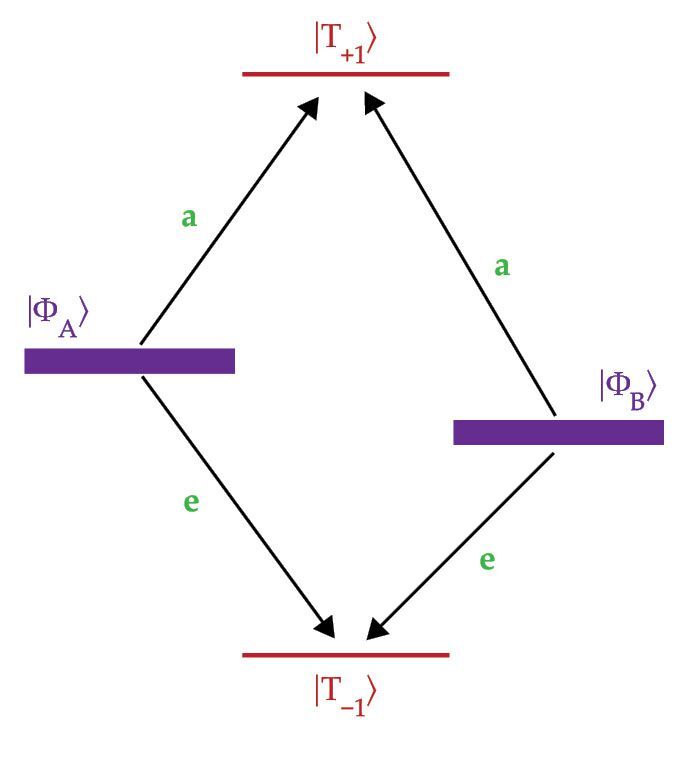
The energy levels for an entangled pair of spins change in a high magnetic field. For a molecular system, the result is the mixing of the singlet
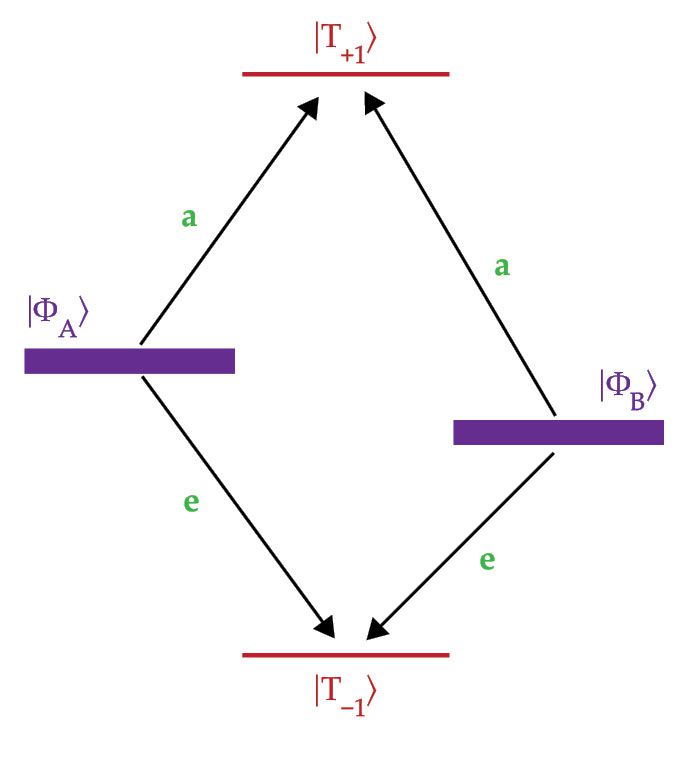
Because the SQP starts in a pure
Many of the interactions quantified by the variables g, a, and D are anisotropic. But they are averaged out in room-temperature TREPR measurements of SQPs in solution. That information can be regained by performing the experiments on solid-state samples. Two methods can transform SQP solutions into solids. Many experiments freeze dilute solutions into a low-temperature glass state. Researchers also employ nematic liquid crystals (LCs) to order D-B-A molecules containing SQPs. 3 The long axis of the LC typically aligns in the direction of an applied magnetic field. The LC in turn aligns the long axis of the surrounding D-B-A molecules parallel to it. Freezing the LC locks in the orientation of the molecule, which can then be rotated relative to the magnetic field direction to explore the anisotropies of g, a, and D.
The distance between the two spins strongly influences the SQP lifetime and
Figure 2.
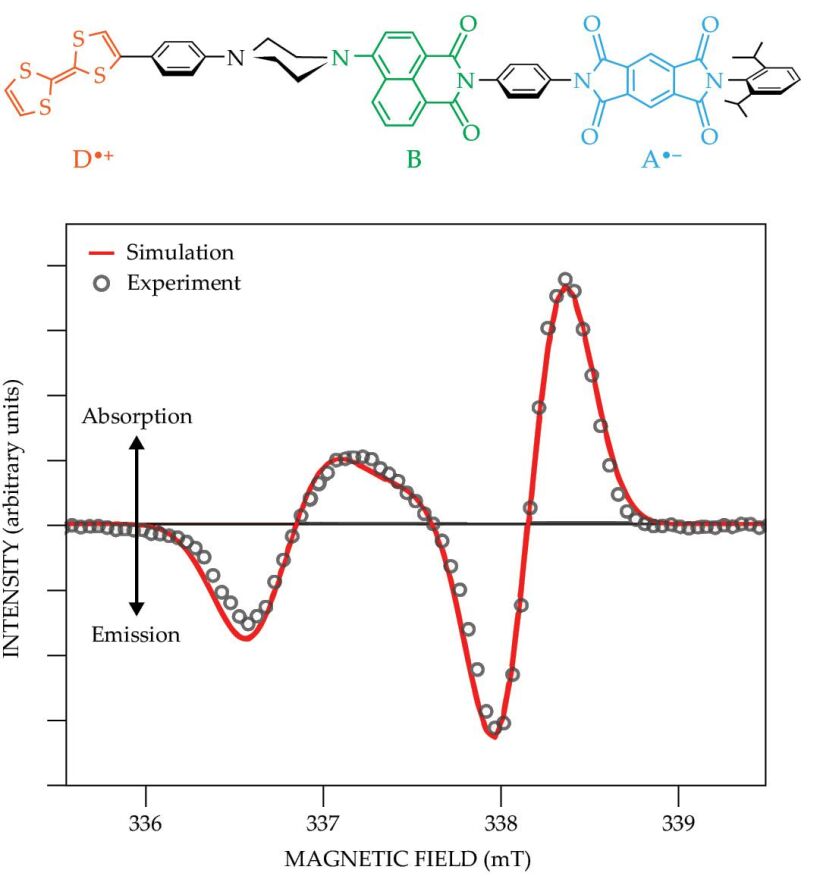
A molecular triad comprises a linked-together tetrathiafulvalene electron donor (D), aminonaphthalimide bridge molecule (B), and pyromellitimide acceptor (A). After being aligned by nematic liquid crystals and frozen into place at 85 K, it has a time-resolved electron paramagnetic resonance (TREPR) spectrum that’s typical for a molecular system hosting a spin-qubit pair. A photoexcited electron moves from D—leaving behind a hole—across B, and to A. The spectrum shown here occurs 100 ns after a laser pulse and has a pattern of emission, absorption, emission, and absorption from low field to high. (Adapted from J. N. Nelson et al., J. Chem. Phys. 152, 014503, 2020, doi:10.1063/1.5128132
Decoherence of SQPs is driven largely by hyperfine interactions between the electrons and nearby nuclei. Reducing the magnetic moments of those nuclei can thus significantly lengthen the coherence time. Although values of a few microseconds are typical for SQPs, recent work in my lab indicates that coherence times approaching 10 µs are readily achievable by swapping the hydrogen atoms in D and A for deuterium, which has a magnetic moment smaller than that of hydrogen by a factor of roughly 6.5.
Molecular SQPs can execute quantum gate operations. Quantum computing requires, for example, the two-qubit controlled-NOT (CNOT) gate, which uses a control bit to set the state of a target bit. If the control bit is off, then the application of a CNOT gate preserves the target bit’s initial on or off state. If the control bit is on, then application of the CNOT gate will flip the target bit from on to off or from off to on. Using the D-B-A molecule in figure
Chirality in molecular spin qubits
Molecules offer a wide variety of properties that can be exploited to control spin states. One such property of growing interest is molecular chirality—that is, handedness. Chirality is a key property of molecules and important in many physical and nearly all biological processes. Ron Naaman, David Waldeck, and their colleagues presented the first evidence of the relationship between chirality and electron motion 7 in 1999. In a thin film of chiral molecules, they observed that far more electrons with one spin polarization passed through the layer than those with the other polarization. Their work was an example of a phenomenon known as chirality-induced spin selectivity (CISS).
When an electron travels along the helical potential generated by a chiral molecule, it experiences a polarizing force from the induced magnetic field. So the transmitted electron mostly ends up with a spin parallel or antiparallel to its motion, depending on the handedness of the chiral molecule. The spin selectivity of the effect can be very high, even at room temperature, and cannot be explained solely by spin–orbit coupling effects, which are relatively weak in molecular structures that are primarily composed of light atoms.
The theoretical foundation of CISS is still being explored, and its potential for spin manipulation relevant to QIS has only recently been recognized. Some fundamental questions that remain are the following: Does CISS affect intramolecular electron transfer for molecules not on a substrate? Can magnetic resonance techniques directly measure the spin polarization created by the CISS effect? Can an electron’s resulting spin polarization be transferred to other quantum spin systems? Can optical methods read out the results of the CISS effect on electron spin states?
If charge transfer occurs through a chiral spacer, denoted as Bχ in D-Bχ-A, the bridge molecule induces a spin polarization that depends on its chirality and the direction of the electron transfer. As a result, electron–hole pairs end up primarily in the
DNA helices, which provided the first observation of the CISS effect on spin dynamics, can also be used as bridge molecules to study the CISS effect on SQP. My colleagues and I recently studied DNA hairpins, so-called to evoke the molecule’s shape.
3
In one example, a naphthalenediimide (NDI) chromophore acceptor molecule links two short single strands of DNA, as depicted in figure
Figure 3.
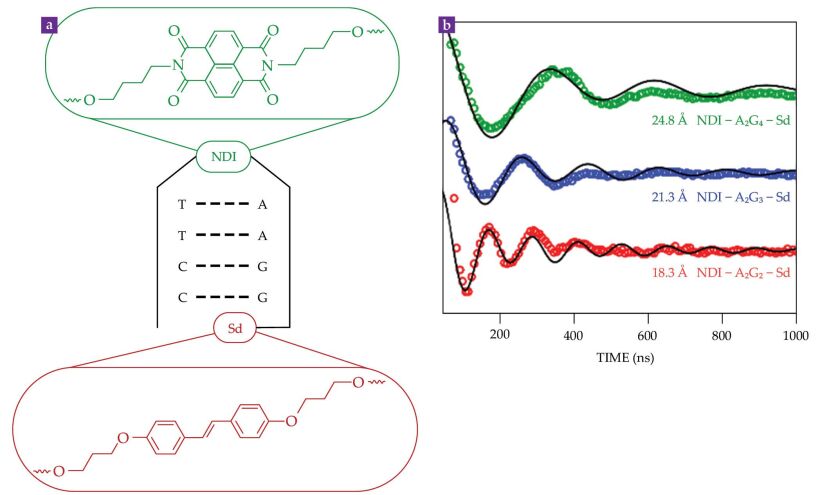
DNA helices can bridge a variable gap between electron spins. (a) A DNA hairpin composed of adenine (A), thymine (T), cytosine (C), and guanine (G) bases connects a naphthalenediimide (NDI) acceptor chromophore to a stilbene diether (Sd) donor molecule to form a single structure such as NDI-A2G2-Sd, shown here. (b) After the formation of a spin-qubit pair at 85 K, what’s known as the out-of-phase electron spin-echo envelope modulation can reveal the distance between the NDI and Sd spins, shown here for three separations (colors) with corresponding simulations (black). (Adapted from J. H. Olshansky et al., J. Am. Chem. Soc. 141, 2152, 2019, doi:10.1021/jacs.8b13155
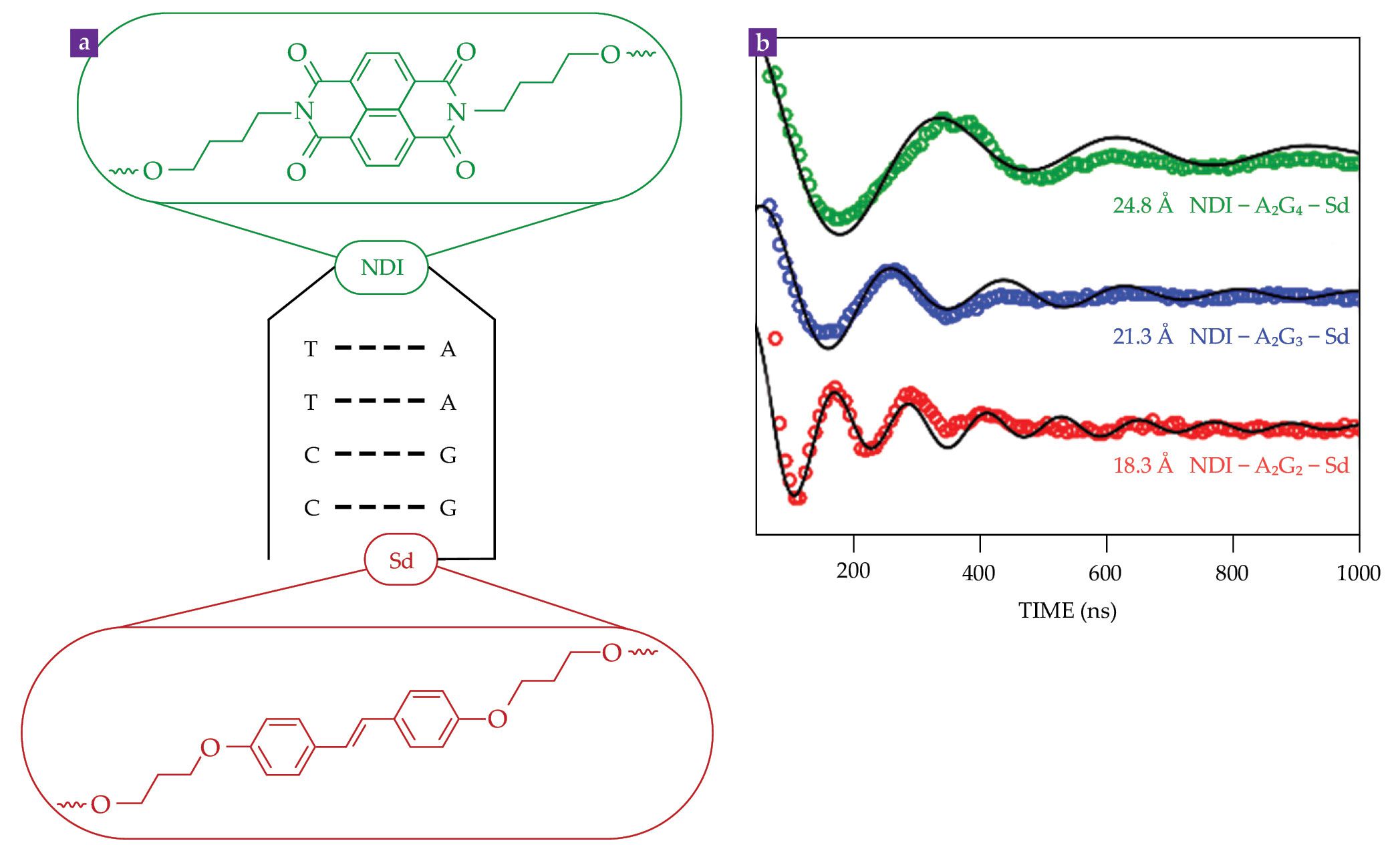
TREPR techniques using pulsed microwaves reveal detailed information about J, D, and spin coherence for photogenerated SQPs in DNA hairpins. For example, say photogeneration of an SQP is followed by a microwave pulse that rotates the spin ensemble away from the direction of the magnetic field (z-direction) into the xy-plane. Local magnetic field variations resulting from the spins’ interactions then cause the spins to fan out in the xy-plane. A second microwave pulse can refocus the spins, resulting in a so-called spin echo. The measured echo amplitude as a function of the interpulse delay oscillates with a frequency related to both J and D. 9
When the experiment is performed on spin-coherent SQPs, the echo experiences a characteristic phase shift relative to the microwave pulses and is therefore termed an out-of-phase electron spin-echo envelope modulation (OOP-ESEEM).
9
If J is small (as it usually is), the OOP-ESEEM oscillation frequency is approximately
Recent theoretical work has shown that based on the phase relationships of spin-echo oscillations, OOP-ESEEM and TREPR in general can detect the CISS effect on the spin dynamics of SQPs.
10
Figure
Adding a third spin
Quantum communications is often depicted as long-range transmission of information, such as establishing secure links to orbiting satellites. But coherent information transfer over length scales ranging from 1 nm to 100 nm is critical for the connections between quantum processors, so-called quantum interconnects. It is in that regime that molecular systems are particularly promising. Those interconnects necessarily involve more than two electron spins, so strategies are needed to deal with multiple spins—for example, quantum teleportation in a three-spin system.
Quantum teleportation is the transfer of a quantum state over an arbitrary distance through quantum entanglement. Copying a quantum state is impossible because measurement destroys the information encoded in a quantum superposition—a phenomenon known as the no-cloning theorem. In 1993 Charles Bennett and colleagues proposed a workaround that uses quantum entanglement to transfer the information without destroying it: 11 Given a particle (particle 1) and a pair of entangled particles (particles 2 and 3), the state of particle 1 can be transferred to particle 3 through a joint so-called Bell-state measurement on particles 1 and 2. Experiments since have demonstrated quantum teleportation in photonic qubits, trapped ions, atomic ensembles, superconducting circuits, nuclear spins, electron spins in quantum dots, and a combination of the electron and nuclear spins of nitrogen–vacancy centers in diamond.
In 2007 Kev Salikhov and his colleagues proposed a method to perform quantum teleportation with an SQP. One electron in the entangled SQP spontaneously transfers to an adjacent stable organic radical that has an unpaired electron prepared in a specific initial spin state. The electron transfer would reduce the third radical to a diamagnetic anion and serve as the Bell-state measurement step. As a result, the third radical’s initial spin state teleports to the remaining member of the original SQP. 12
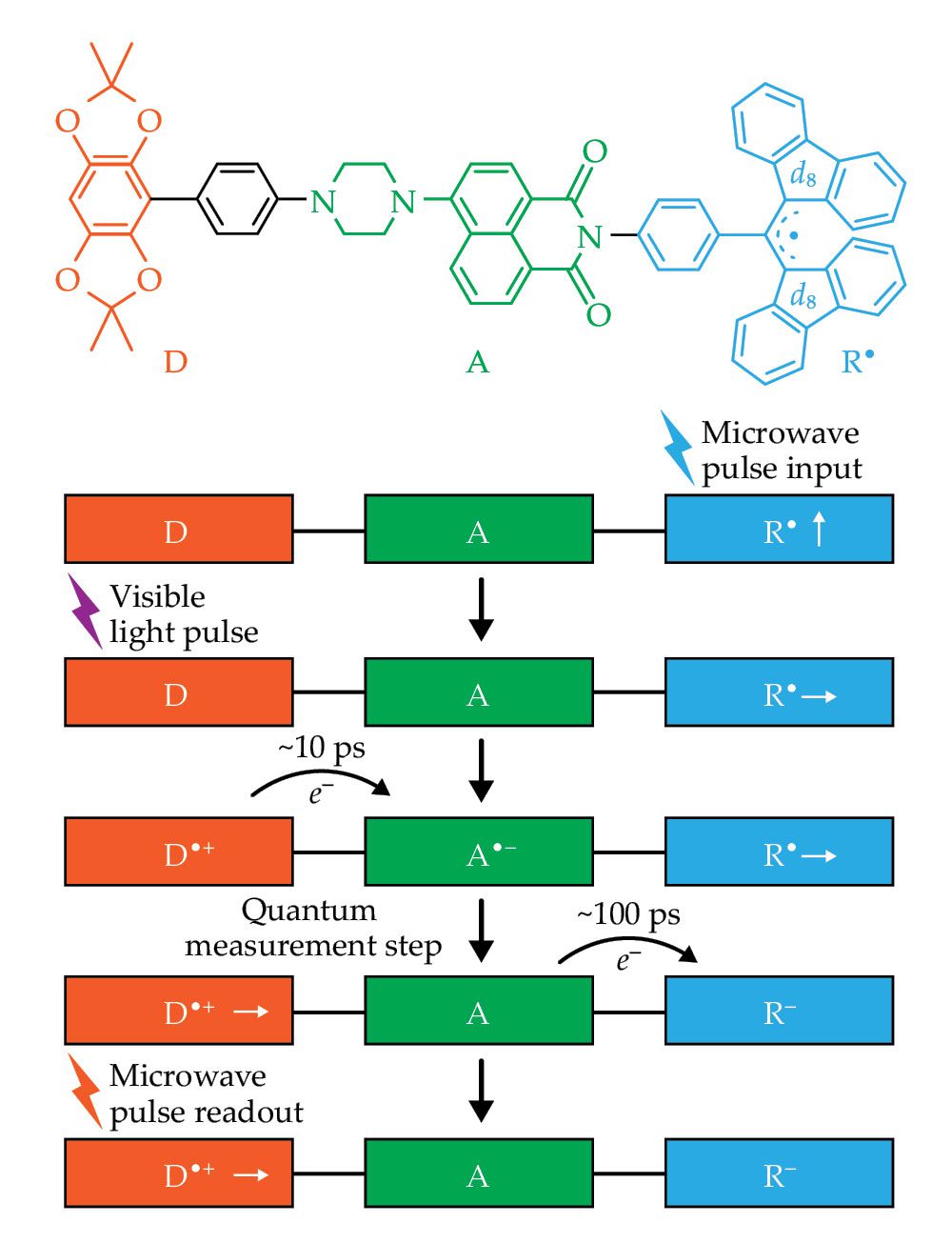
Using that strategy, my colleagues and I implemented quantum teleportation in a donor-acceptor-stable radical (D-A-R•) molecule, shown in figure
Figure 4.
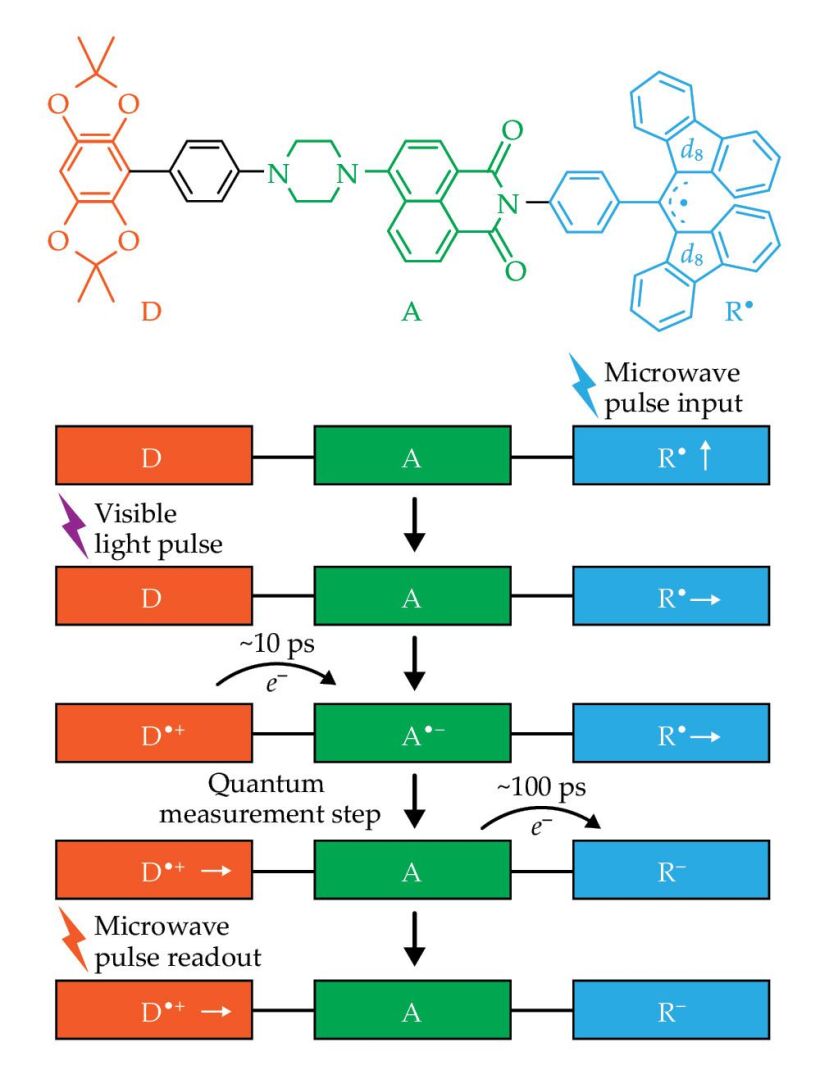
Quantum teleportation is possible in the donor-acceptor-stable radical (D-B-R•) molecule, shown at top, composed of tetramethylbenzodioxole (D), aminonaphthalimide (A), and α,γ-bisdiphenylene-β-phenylallyl (R•). (The label d8 indicates that the fluorenyl rings are deuterated.) In the teleportation scheme at bottom, a microwave pulse puts R• in a selected spin state. A visible laser pulse then excites an electron e–, which in about 10 ps transfers from D to A and forms an entangled pair with the hole it left behind. When the electron transfers to R•, the process is equivalent to a measurement. As a result, the initial spin state at R• is teleported to the hole at D•+, where its state can be read out by microwave pulses.
Another promising approach to create and manipulate three-molecular-qubit systems employs an optically excited chromophore covalently linked to a stable radical. For example, recent work has focused on perylenediimide (PDI) chromophores, which are widely available, robust organic dyes used in some red paint formulations. My colleagues and I linked PDI to the stable BPDA radical, which following photoexcitation of PDI produces a spin-polarized quartet state that subsequently transfers its spin polarization to the doublet ground state of the BPDA radical. 14 Using optical pumping to spin polarize a stable radical is an important outcome because it can be used for QIS applications in a manner analogous to the way defect sites in diamond or silicon carbide are used. But molecular systems have the advantage of being easily modified and placed at spatially precise locations.
Four for the price of one
Singlet fission (SF) is a process in which a photoexcited molecule in its excited singlet state interacts with a neighboring molecule in its ground state 15 such that the molecules end up in a pair of coupled triplet states 1(TT) with an overall singlet spin state (S = 0). Although SF has been known about for about 50 years, it has attracted considerable interest recently as a way to improve the performance of solar cells. In the past five years or so, researchers have also realized that SF is an efficient way to use one photon to prepare four entangled molecular spin qubits. 16 , 17 In an organic semiconductor, the rate of SF depends on how strong the interaction is between the neighboring molecules and the energies of the singlet and triplet excitons, ES and ET, respectively—rapid rates are achieved when ES ≥ 2ET.
If the 1(TT) lifetime is sufficiently long, spin evolution can produce the quintet (S = 2) state 5(TT), which has four unpaired electrons, before the spins eventually decohere,
16
as depicted in figure
Figure 5.
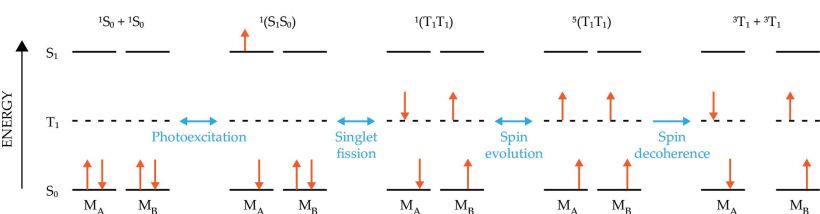
Figure 5. Singlet fission uses a single photon to generate four spin qubits. A pair of molecules (MA and MB) start in their ground states S0. After photoexcitation, MA enters its singlet state S1. The two molecules then interact such that they both end up in excited triplet states T1. After enough time, the spins can evolve to form a five-level state 5(T1T1) that has four unpaired electrons. Eventually the spins decohere altogether.
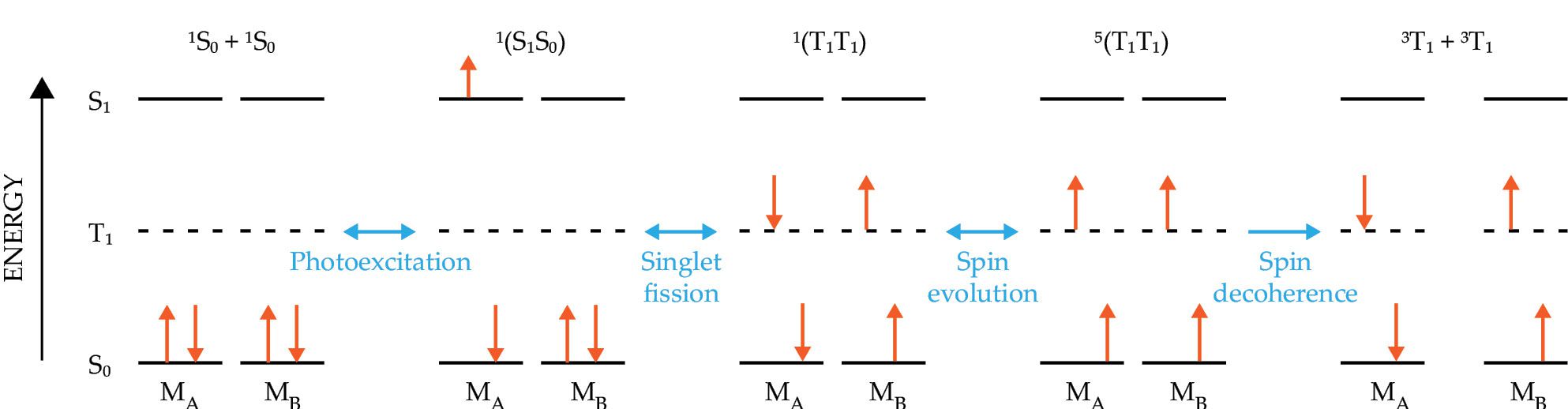
Several other qualities of the 5(TT) state also make it attractive for QIS applications. Because of its many possible spin orientations, the 5(TT) state can be utilized as a five-level qudit—the multilevel analog of the two-level qubit. Qudits could facilitate greater storage and processing power than qubits and may provide built-in error correction. The 5(TT) state can also be photogenerated on demand at arbitrary locations. Despite the 5(TT) state’s intriguing properties, investigations of it for QIS applications have been limited thus far. The mechanisms of its decoherence are not yet well understood, and strategies for extending coherence lifetimes have not been fully realized.
Although SF occurs in molecular dimers and higher aggregates of chromophores 15 in both solution and the solid state, the 5(TT) state has been relatively elusive in solid-state materials. To realize a long-lived 5(TT) state, the intermolecular electronic interaction must be sufficiently strong to allow efficient SF and prevent dissociation of the triplet-pair state but sufficiently weak to minimize triplet–triplet annihilation and triplet diffusion. Striking that delicate balance is a major challenge. In solid-state materials, electronic coupling is dictated by the crystal structure, which is difficult to predict or control because of the various weak intermolecular forces that govern molecular packing. 16
Recently some colleagues and I have managed to engineer the crystal morphology of the chromophore tetracene. 17 By attaching bulky tris(cyclohexyl)silylethynyl groups to it, adjacent pairs of tetracene molecules are placed far enough apart in the crystal to be effectively isolated. Photoexcitation of tetracene results in formation of the 5(TT) state, which is confirmed by its TREPR spectrum and observable even at room temperature. The lifetime of the 5(TT) state is 130 μs, and its spin-coherence lifetime is 3 μs at 5 K. The crystals spatially align and organize the interchromophore spacing to optimize the electronic interaction needed for favorable 5(TT) properties. With that optimization taken care of, future work can focus on identifying decoherence sources.
Scaling up and outlook
Light-driven processes in molecules are increasingly revealing themselves as promising spin qubits. The coherence lifetimes of those systems are constantly improving through, for example, deuteration of the organic molecules. Molecular spin qubits have already demonstrated basic operations essential to QIS, such as transferring coherence and polarization to neighboring spins and essential quantum gate operations, including the CNOT gate. Further work on spin teleportation in molecular arrays will extend the distance over which quantum information can be transferred from the nanoscale to the microscale.
Now that some of the basic concepts intrinsic to quantum information have been demonstrated, further development of photogenerated molecular spin qubits will likely take many directions. For example, multispin systems comprising even a few qubits can execute simple algorithms and serve as intelligent nanoscale sensors. A key challenge to those and other applications is finding ways to photogenerate larger numbers of SQPs and control individual spins. Toward that goal, two colleagues and I have already shown that it is possible to generate two SQPs in a single molecular system by using laser pulses at two wavelengths. 18
Exploiting the CISS effect in molecular systems may make it possible for molecular building blocks to execute well-defined spin manipulations similar to what is achieved today using microwave pulses. Different molecular building blocks that execute different spin manipulations could combine to create functional molecular quantum circuits on the nanoscale. Lastly, DNA hairpins and other systems that mimic nature provide a readily accessible platform to scale up molecular quantum components. Exploiting chemistry to create new multispin systems provides a broad range of new molecules and materials whose properties can be tailored to specific QIS applications.
This work was supported as part of the Center for Molecular Quantum Transduction, an Energy Frontier Research Center funded by the US Department of Energy, Office of Science, Basic Energy Sciences, under award DE-SC0021314.
References
1. M. R. Wasielewski et al., Nat. Rev. Chem. 4, 490 (2020). https://doi.org/10.1038/s41570-020-0200-5
2. P. J. Hore, C. G. Joslin, K. A. McLauchlan, Chem. Soc. Rev. 8, 29 (1979). https://doi.org/10.1039/cs9790800029
3. S. M. Harvey, M. R. Wasielewski, J. Am. Chem. Soc. 143, 15508 (2021). https://doi.org/10.1021/jacs.1c07706
4. D. P. DiVincenzo, Fortschr. Phys. 48, 771 (2000). https://doi.org/10.1002/1521-3978(200009)48:9/11<771::AID-PROP771>3.0.CO;2-E
5. G. L. Closs, M. D. E. Forbes, J. R. Norris, J. Phys. Chem. 91, 3592 (1987); https://doi.org/10.1021/j100297a026
C. D. Buckley et al., Chem. Phys. Lett. 135, 307 (1987); https://doi.org/10.1016/0009-2614(87)85162-X
A. J. Hoff et al., Spectrochim. Acta A Mol. Biomol. Spectrosc. 54, 2283 (1998). https://doi.org/10.1016/S1386-1425(98)00211-X6. J. S. Bell, Phys. Phys. Fiz. 47, 195 (1964). https://doi.org/10.1111/j.1444-0938.1964.tb01735.x
7. K. Ray et al., Science 283, 814 (1999); https://doi.org/10.1126/science.283.5403.814
R. Naaman, Y. Paltiel, D. H. Waldeck, Nat. Rev. Chem. 3, 250 (2019). https://doi.org/10.1038/s41570-019-0087-18. J. Luo, P. J. Hore, New J. Phys. 23, 043032 (2021). https://doi.org/10.1088/1367-2630/abed0b
9. J. Tan, M. C. Thurnauer, J. R. Norris, Chem. Phys. Lett. 219, 283 (1994). https://doi.org/10.1016/0009-2614(94)87059-4
10. T. P. Fay, J. Phys. Chem. Lett. 12, 1407 (2021); https://doi.org/10.1021/acs.jpclett.1c00009
A. Chiesa et al., J. Phys. Chem. Lett. 12, 6341 (2021). https://doi.org/10.1021/acs.jpclett.1c0144711. C. H. Bennett et al., Phys. Rev. Lett. 70, 1895 (1993). https://doi.org/10.1103/PhysRevLett.70.1895
12. K. M. Salikhov, J. H. Golbeck, D. Stehlik, Appl. Magn. Reson. 31, 237 (2007). https://doi.org/10.1007/BF03166259
13. B. K. Rugg et al., Nat. Chem. 11, 981 (2019). https://doi.org/10.1038/s41557-019-0332-8
14. Y. Qiu et al., Angew. Chem. Int. Ed. 62, e202214668 (2023). https://doi.org/10.1002/anie.202214668
15. M. B. Smith, J. Michl, Chem. Rev. 110, 6891 (2010). https://doi.org/10.1021/cr1002613
16. L. R. Weiss et al., Nat. Phys. 13, 176 (2017). https://doi.org/10.1038/nphys3908
17. R. M. Jacobberger et al., J. Am. Chem. Soc. 144, 2276 (2022). https://doi.org/10.1021/jacs.1c12414
18. M. P. Debreczeny, W. A. Svec, M. R. Wasielewski, Science 274, 584 (1996). https://doi.org/10.1126/science.274.5287.584
More about the authors
Michael Wasielewski is the Clare Hamilton Hall Professor of Chemistry, director of the Center for Molecular Quantum Transduction, and executive director of the Institute for Sustainability and Energy at Northwestern University in Evanston, Illinois.





