Large amplitude oscillatory shear: Simple to describe, hard to interpret
DOI: 10.1063/PT.3.3971
Silly Putty, the classic toy that can stretch, bounce, snap, and mold, provides endless hours of amusement. It is an elastic liquid, so-called because it simultaneously exhibits both solid-like (elastic) and liquid-like (viscous) behaviors. The viscoelasticity of Silly Putty is evidenced by the way it bounces off a table like a rubber ball when interacting quickly with the surface and flows like a thick syrup when left alone for a long time. Is Silly Putty a solid or a liquid? The answer depends on the time scale over which it is observed. Typical viscoelastic materials are elastic at short times and viscous at long times.
Many important and familiar substances are viscoelastic. Examples include biological and industrial macromolecules, colloidal suspensions, emulsions, and foams. The characteristic time that separates short-term from long-term behavior is specific to each material and governed by the rate at which the material can relax stress. That relaxation time is a macroscopic manifestation of the microscopic processes by which molecular or mesoscopic constituents rearrange themselves when the bulk material is deformed. Think of entangled polymers moving like spaghetti on your plate when you twist your fork, with each noodle-like polymer moving around its neighbors. Or imagine clusters of colloidal particles, such as those shown in figure
Figure 1.

Toothpaste, yogurt, paint, and many other common materials are colloidal gels, in which solid particles are dispersed in a liquid. In this simulation of a colloidal gel deformed with large amplitude oscillatory shear, colors indicate clusters of colloidal particles. (Courtesy of Jun Dong Park, University of Illinois at Urbana-Champaign.)

Viscoelasticity spans the space between the behaviors of elastic solids, in which stresses and strains are proportional, and those of viscous liquids, in which stresses and strain rates are proportional. Measurements of viscoelasticity require a way of probing a material’s solid-like and liquid-like responses simultaneously. By far the most common experimental approach is to apply a shear strain that varies sinusoidally in time and measure the stress response, a test devised by Andrew Gemant
1
in 1935. Figure
Figure 2.

At the heart of a typical rheometer (a) is a working fluid, here a variety of blue Colgate MaxFresh toothpaste, sandwiched between a lower plate and an upper surface that apply a shear strain. A transducer located above the frame of the photo converts the fluid’s stress response into a measurable electronic signal. (b) Oscillatory shearing is described by two parameters with units of inverse seconds, the amplitude
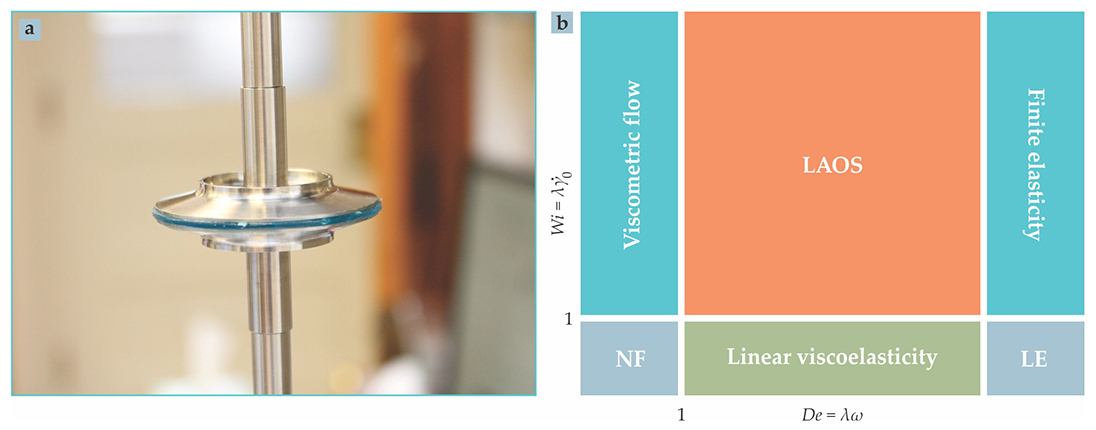
The
How do we explore material responses to large strains? For that matter, how large is large?
Box. Linear viscoelastic response
If a material is not deformed too much, the effects of sequential changes in strain are additive. To calculate the linear rheological response of a viscoelastic material, I turn to the Boltzmann superposition principle, which states that the stress
Let
The terms in the large parentheses are functions of frequency only, so the response to oscillatory strains may be expressed as
Equation
Unexplored territory
The oscillatory strain used to probe the solid-like and liquid-like components of viscoelasticity has two tunable parameters: the frequency of the oscillation, which governs the time scale being probed, and the amplitude, which governs the extent of the deformation. Both parameters can be expressed in dimensionless form to account for material-specific relaxation processes.
For oscillatory testing, the Deborah number
One can think of all oscillatory responses as residing in the space defined by those two dimensionless numbers. A loosely defined version of that space, reproduced here as figure
Linear viscoelasticity—output linearly dependent on input—corresponds to small-amplitude oscillations. The relaxation time of a material is typically determined in the linear regime by taking the reciprocal of the frequency at which the dynamic storage and loss moduli, described in the
For the biggest region of the space defined by Pipkin, however, strain amplitudes are large and frequencies are neither high nor low. Experiments probing that region are called large amplitude oscillatory shear (LAOS) tests. As a consequence of the study of LAOS, linear viscoelastic oscillations are now referred to as small amplitude oscillatory shear, or SAOS. Some experimenters use MAOS for medium amplitudes, and at least one researcher has suggested XXLAOS for extra-extra-large amplitudes. 2 Noting the proliferation of naming schemes, MIT’s Gareth McKinley, in his plenary lecture at the International Congress on Rheology in Lisbon, Portugal, in 2012, put forward the tongue-in-cheek suggestion that CHAOS enter the rheological nomenclature. Despite the various naming options, many researchers take a binary approach: The nonlinearities that exist in all real experiments are either insignificant or too small to measure, in which case the experiment is SAOS, or they are significant and the study is LAOS.
We researchers who conduct LAOS experiments cannot treat the response as a sum of purely viscous and purely elastic terms. Rather, we are forced to take into account the inherent viscoelasticity. Typically, the response to a sinusoidal input in the LAOS region is not sinusoidal. Pipkin himself noted that “nothing very systematic” is known about the region of large
Linear oscillatory rheology has been studied for more than 80 years in SAOS experiments, but LAOS studies have become commonplace only in the past couple of decades, with the advent of more sensitive transducers in commercially available rheometers. In that time, investigations have used LAOS on a large variety of materials, including biological macromolecules, polymer melts and solutions, blends of polymers, block copolymers, polyelectrolytes, surfactants, suspensions, and emulsions.
To the brink and back
Why are LAOS studies important? To some extent I addressed that question when I noted that researchers seek protocols that match the nonlinear and transient processing conditions imposed on real-world materials. In a LAOS test, an investigator can control large, rapid deformations. LAOS is therefore a well-defined standard protocol for obtaining information regarding a material’s nonlinear viscoelasticity and the transient way it changes in response to those deformations.
Two types of transience and nonlinearity are involved in LAOS tests. Intercycle and intracycle measures, as the prefixes suggest, provide information regarding changes between successive oscillations and changes in a single oscillation. Intercycle measures can be used, for instance, to determine how long it takes for a material to reach a steady-state oscillating response. Once at steady-state, intracycle measures on the material can help explicate the nonlinear way in which the material responds to strains and strain rates.
Different materials that have similar linear rheology can have drastically different nonlinear rheology, and thus their response to LAOS can provide information not available from linear measurements. For example, LAOS can help differentiate between suspensions of rigid and soft particles that would look the same in SAOS experiments.
A LAOS study is an oscillatory protocol, but a second class of transient protocols—steps—is also often used by researchers. In a step experiment, the strain or the rate of strain is suddenly changed, and the material’s response is recorded as a function of time elapsed from the moment of change. For the nonlinear rheological properties to be explored in the clearest conceptual manner, the steps need to be large and instantaneous. A literal instantaneous jump is not possible, and even tests that approximate the instantaneous jumps with large ramps place considerable loads on the materials and the testing equipment and can lead to failure of one or both. In contrast, oscillatory methods are gentle; they impose smoothly changing deformations with no sudden jumps. Deformations that would lead to material failure in step tests can be applied in oscillatory tests. Like the Road Runner being chased off a cliff by Wile E. Coyote, materials in a LAOS experiment can turn back and avert disaster.
Fourier-transform rheology
As I noted earlier, once more sensitive transducers became widely available in commercial rheometers, investigators could perform LAOS experiments that provided clean, reliable data. The next major challenge for the community to overcome—still an active and ongoing avenue of research—is what to do with experimental data once we’ve got them. That is, how do we obtain meaning from the results? What formalism provides clear and unambiguous physical interpretations in all cases? The community has not reached consensus; in fact, the most popular approach has changed numerous times in the past decade. To date, the most useful avenues have relied on 19th-century mathematics and are associated with the way LAOS data are presented.
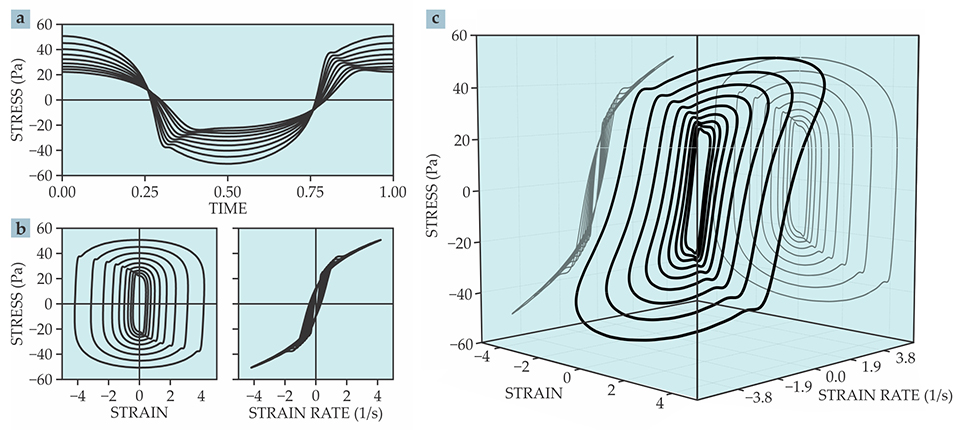
When a material is probed by LAOS, the sinusoidal strain and strain-rate inputs and the nonsinusoidal stress output are recorded. Displaying the stress as a function of time, as shown in figure
Figure 3.

Display methods for large amplitude oscillatory shear data are connected with the type of analysis used. (a) A nonlinear periodic stress response plotted as a function of time invites a Fourier transform, which yields the spectrum of frequencies for the response. (b) When the stress is plotted as a function of either the strain or the strain rate, it is natural to look for linear relations—that is, regions where the derivatives are constant. (c) Stress plotted as a function of both the strain and the strain rate is usefully described in terms of the geometry of trajectories in deformation space. (All panels adapted from ref.
One of the group’s notable successes started from an idea discussed earlier, that the viscoelastic response of a material is a result of the way its constituents rearrange when deformed. Wilhelm, joined by Kyu Hyun of Pusan National University in South Korea and Victor Hugo Rolón Garrido and Manfred Wagner, both of the Technical University of Berlin, showed that nonlinear oscillatory rheology can differentiate between polymers with different branching structures. 4 The group coupled LAOS experiments with Wagner’s molecular stress function theory and showed that the theory was able to account for the scaling relations observed during frequency and amplitude sweeps. For example, theory and experiment are in accord that the ratio of third-harmonic intensity to first-harmonic intensity is proportional to the square of the strain amplitude.
Despite the widespread use of FT rheology, there remains no clear physical interpretation of the experimentally measured higher harmonics for an arbitrary material. Recent theoretical work from a Thai–Canadian collaboration has produced exact expressions for the higher harmonics in terms of the parameters of some simple models for LAOS flow, though it is not yet clear how generally those expressions can be applied. 5 Studies of LAOS using FT approaches typically follow the tack of Wilhelm and colleagues and combine experimental results with model predictions. The lack of a clear analytic strategy has led researchers to propose other formalisms that lend themselves to more straightforward physical interpretation.
A consensus broken
Several researchers have advocated displaying the results of an oscillatory test as Lissajous figures, parametric plots of oscillating signals first studied by Nathanial Bowditch in 1815. (Jules Antoine Lissajous published his work in 1857.) Plotting stress parametrically against the strain or the strain rate, as shown in figure
In 2005 Kwang Soo Cho from Kyungpook National University and Kyu Hyun, Kyung Hyun Ahn, and Seung Jong Lee at Seoul National University in South Korea used symmetry arguments in proposing a decomposition of the stress into two constructions they referred to as the elastic and viscous stresses. 6 Cho and coworkers defined those as even and odd functions of the strain and strain rate and showed that they can be obtained from the elastic and viscous Lissajous curves. Unlike the Lissajous figures from which they are derived, however, elastic and viscous stresses are single-valued in the strain and the strain rate: With Cho and colleagues’ innovation, the complexity of describing shapes had been reduced to the simpler task of describing lines.
Three years after the publication of Cho’s stress decomposition, Randy Ewoldt, Anette “Peko” Hosoi, and McKinley, all from MIT, suggested that Chebyshev polynomials of the first kind would be a useful linear algebraic basis for describing Cho’s elastic and viscous stresses. 7 Using the polynomials introduced by Pafnuty Chebyshev in 1854, Ewoldt and coworkers proposed physical interpretations for the first two terms in the expansions of Cho’s elastic and viscous stresses. For example, Ewoldt and coworkers argued that a positive coefficient of the third Chebyshev polynomial in the description of Cho’s elastic stress leads to a greater stress at large strains than would occur if only the linear term were present. Such an increase signifies strain stiffening. A positive value for the analogous component in the expression for the viscous stress would be indicative of shear thickening.
The LAOS community greeted Ewoldt and coworkers’ physical interpretations with excitement, particularly because the theorists had also shown that the Chebyshev analysis was simply related to the often used Fourier analysis. In fact, Fourier transformation, the stress decomposition, and the Chebyshev description were ultimately shown to be different expressions of the same underlying structure.
The field of LAOS analysis seemed to have reached a point of near consensus, with researchers free to choose among the three equivalent major analysis frameworks. That consensus was broken when Pavlik Lettinga and I, working at the Jülich Research Center in Germany, published work in which we used simple models to show that the physical interpretations derived from those frameworks could not be applied to all LAOS responses. 8 The mathematics was sound, but the physical interpretations were more limited than had been thought because the symmetries assumed by Cho and coworkers in their stress decomposition were not always present. Given the clear connection between the Fourier transformation, stress-decomposition, and Chebyshev approaches, our exposition was problematic. Another approach was needed.
Some investigators sought to describe the overall shape of the Lissajous figures in a manner akin to the way Fourier transformation views the entire period of oscillation as the object to be described. Others, including me, took a different approach and looked for parts of the response, as represented by the Lissajous figures, that are locally linear. Those regions could be easily interpreted as representing a sequence of physical, elastic and viscous processes. Armed with that insight, Dimitris Vlassopoulos, Brian Erwin, and I, all at the Foundation for Research and Technology–Hellas in Greece, along with Michel Cloitre from ESPCI ParisTech considered a glassy suspension of star-shaped polymers.
9
By following sequences of elastic and viscous processes, we were able to show that the LAOS response of the glassy colloid (see figure
More recently, I have further developed the concept of physical-process sequences,
10
starting from an observation made originally by Cho and coworkers.
6
They had noted that viscoelastic responses lie on a two-dimensional surface in the space defined by the strain, the strain rate, and the stress. Figure
Beyond stress measurements
The fundamental thesis underlying studies of viscoelasticity, including those that use LAOS experiments, is that the macroscopic response is a manifestation of microscopic processes. Researchers have done much work to deduce the microstructural response of a material from its rheology, but, more and more, researchers are using powerful structural techniques to measure how material constituents rearrange. Approaches that combine rheological information with structural probes include rheo-NMR 11 and rheo-scattering. 12
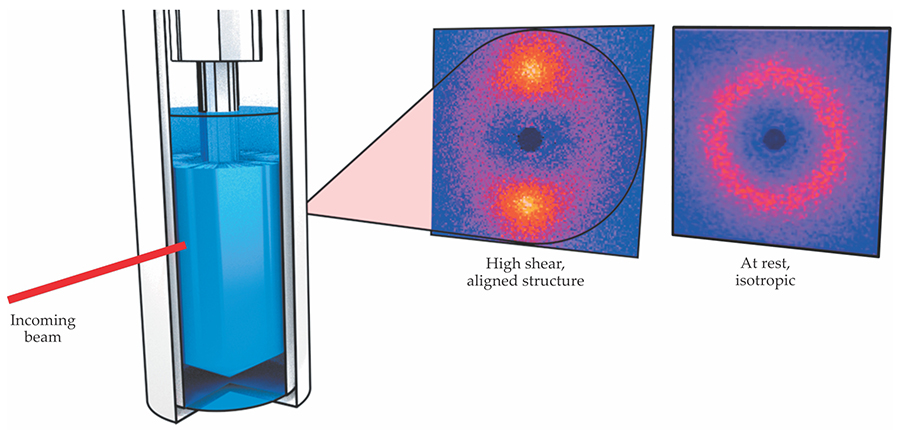
Hybrid experiments typically include a rheometer in an external magnetic field or a beam of laser light, x rays, or neutrons in such a way that the NMR or scattering experiment can proceed normally as the material is subjected to a controlled deformation; figure
Figure 4.

Hybrid rheo-scattering experiments involve scattering light, x rays, or neutrons from samples undergoing deformation. In the left panel, a cylindrical rotating bob immersed in a fluid sets up a shear field. Scattering provides information relating the microstructure to the rheology. In this example, the fluid includes polymer-like micelles, clusters of colloidal molecules. Shearing at high rates aligns the micelles and leads to an anisotropic scattering pattern (central panel; yellow indicates greatest scattering and blue least). In contrast, when the material is at rest, the scattering pattern is isotropic (right panel).
As rheologists more deeply explore the transient nonlinear viscoelasticity of soft materials and discover more about the ways in which their constituents move and rearrange, we also deepen our understanding of the testing protocols and learn how to design more specialized experiments. The more we learn about the sometimes subtle, sometimes drastic changes that occur during deformation, the more we will be able to incorporate those lessons into the design of a new generation of smart materials.

The author, Simon Rogers, at work. (Photograph by L. Brian Stauffer, University of Illinois at Urbana-Champaign.)

References
1. A. Gemant, Trans. Faraday Soc. 31, 1582 (1935). https://doi.org/10.1039/tf9353101582
2. R. H. Ewoldt, J. Fluid Mech. 798, 1 (2016). https://doi.org/10.1017/jfm.2016.265
3. M. Wilhelm, Macromol. Mater. Eng. 287, 83 (2002). https://doi.org/10.1002/1439-2054(20020201)287:2<83::AID-MAME83>3.0.CO;2-B
4. M. Wagner et al., J. Rheol. 55, 495 (2011). https://doi.org/10.1122/1.3553031
5. C. Saengow, A. J. Giacomin, C. Kolitawong, Macromol. Theory Simul. 24, 352 (2015); https://doi.org/10.1002/mats.201400104
C. Saengow, A. J. Giacomin, C. Kolitawong, Phys. Fluids 29, 043101 (2017). https://doi.org/10.1063/1.49789596. K. S. Cho et al., J. Rheol. 49, 747 (2005). https://doi.org/10.1122/1.1895801
7. R. H. Ewoldt, A. E. Hosoi, G. H. McKinley, J. Rheol. 52, 1427 (2008). https://doi.org/10.1122/1.2970095
8. S. A. Rogers, M. P. Lettinga, J. Rheol. 56, 1 (2012). https://doi.org/10.1122/1.3662962
9. S. A. Rogers et al., J. Rheol. 55, 435 (2011). https://doi.org/10.1122/1.3544591
10. S. A. Rogers, Rheol. Acta 56, 501 (2017). https://doi.org/10.1007/s00397-017-1008-1
11. P. T. Callaghan, Rep. Prog. Phys. 62, 599 (1999). https://doi.org/10.1088/0034-4885/62/4/003
12. A. K. Gurnon et al., Soft Matter 10, 2889 (2014). https://doi.org/10.1039/C3SM53113A
More about the authors
Simon Rogers is an assistant professor in the department of chemical and biomolecular engineering at the University of Illinois at Urbana-Champaign.





