Iron-based superconductors: Teenage, complex, challenging
DOI: 10.1063/PT.3.5235
The annual meeting of the American Physical Society in March 2008 was especially memorable for condensed-matter physicists. It seemed that all anyone wanted to talk about in New Orleans was the surprising discovery, and subsequent confirmation, of high-temperature superconductivity in the iron arsenides. 1 Surprising was perhaps an understatement. After all, iron was supposed to be as toxic to superconductivity as arsenic is to humans. The superconducting transition temperature Tc had reached only 26 K by the time of the March Meeting, though reports were circulating that—as with high-Tc cuprates two decades earlier—the application of high pressures was pushing Tc to temperatures above 40 K. The race was on.

B. BRYANT

In a matter of weeks after the meeting, substitutional studies had helped to repeatedly break the Tc record, which eventually plateaued at 56 K. As a barometer of the excitement, by the end of 2010, 8 out of 10 of the most cited papers published in Physical Review Letters in 2008 featured arsenide superconductivity. Amid the frenzied activity, superconductivity was also being reported in a simple binary iron chalcogenide, iron selenide. Although the Tc of FeSe was modest—only 8 K in the bulk—in monolayer form it went on to claim the record for all the iron-based superconductors (FeSCs), with a Tc in excess of 65 K. To date, only the cuprates are known to possess a higher Tc at ambient pressure. And although the maximum Tc in either system has not shifted in the past decade, the field of superconductivity is now enjoying a resurgence, spurred on by the discovery of unconventional or high-temperature superconductivity in a host of new materials and extreme environments.
It is therefore an opportune moment for a status update on FeSCs. Because the early years of FeSC research were expertly surveyed in 2009 (see the article by Charles Day, Physics Today, August 2009, page 36
FeSCs allow for a deeper understanding of such diverse themes as electronic nematicity (that is, orientational order), quantum criticality, orbital-selective correlations, and topological superconductivity. Thus, even though FeSCs are still in their teenage years, they are already providing profound insights into the rich physics of unconventional superconductivity.
Some basics
Iron-based superconductors primarily comprise iron pnictides—compounds based on arsenic or another element from the pnictogen group, also known as the nitrogen group, of the periodic table—and iron chalcogenides containing selenium, tellurium, or sulfur. A broad spectrum of structural types exists among those superconductors (see box
Iron-based superconductors—some basics
The various iron-based superconductor (FeSC) family members and their maximal Tc values are listed in panel a. The highest critical transition temperature Tc appears in monolayer iron selenide deposited on a SrTiO3 substrate (FeSe/STO). The accepted record value of Tc, which is based on the onset of the Meissner effect, is 65 K, though transport evidence for Tc above 100 K has also been reported.

All FeSCs have the same structural motif, a single layer of FeSe/FeTe or FeAs/FeP. (For an illustration of the structure of bulk FeSe, which corresponds to direct stacking of FeSe layers, see panel b.) The primitive unit cell of a single FeAs/FeSe layer is shown in panel c, with two Fe ions from an Fe layer, one Se or As ion located above the Fe layer, and one below. When spin-orbit coupling is neglected, the Brillouin zone can be unfolded to a square in reciprocal (k) space, shown in panel d. The unfolded Brillouin zone corresponds to the square lattice of Fe ions illustrated in panel c.
Strictly speaking, one needs to use the two-Fe unit cell and its associated Brillouin zone, which is half of what is shown in panel d. While the notation is rigorous, it is also somewhat cumbersome. Usually, it is more convenient to adopt the single-Fe unit cell and its associated Brillouin zone. Correspondingly, microscopic theoretical studies typically involve multiorbital models on a square lattice with both on-site Hubbard (direct Coulombic) and Hund’s (spin-exchange) interactions.
The electronic states near the Fermi energy are dominated by the 3d orbitals of the Fe ions. Thus, for most purposes, theoretical models of FeSCs retain only the 3d states, with the p orbitals of Se/As ions (or their variants, Te/P ions) projected out. The multiplicity of the 3d orbitals near the Fermi energy is reflected in the multiple Fermi sheets. Most FeSCs have hole Fermi pockets near the center of the one-Fe Brillouin zone and electron pockets at the edges. The hole and electron Fermi pockets have roughly the same size, which enhances the phase space for interpocket electron interactions; they are called “nested.” A single-layer FeSe/STO has only electron Fermi pockets near the edges of the Brillouin zone, as shown in panel d. The same is true in most members of the bulk iron chalcogenides with relatively high Tc, including the alkaline iron selenides, where Tc reaches about 30 K, and the lithium-intercalated iron selenides (Li,Fe)OHFeSe, whose Tc exceeds 40 K. Those members are marked in blue in panel a.
In any crystal, atoms form a periodic arrangement in a lattice. The discrete lattice in real space implies, by virtue of a Fourier transform, a corresponding lattice in reciprocal (that is, wavevector) space. Condensed-matter physicists call the unit cell of that reciprocal space a Brillouin zone. Only a single Brillouin zone is needed to account for all the electronic states.
For a metal, the Pauli exclusion principle dictates that each wavevector be associated with an individual and distinct set of internal (for example, spin and orbital) quantum numbers. For a noninteracting electron system, the electrons occupy states with wavevectors that are associated with an increasing ladder of energies. The locus of wavevectors corresponding to the highest energy—the so-called Fermi energy—of occupied states forms a Fermi surface. The Brillouin zone of a square lattice is another simple square. For some iron chalcogenides in the group of highest-Tc FeSCs, including monolayer FeSe, the Fermi surface also turns out to be remarkably simple, comprising only small electron pockets located at the edges of the Brillouin zone (see box
Electron correlations
When two electrons occupy either the same 3d orbital or two different 3d orbitals of an Fe ion, their proximity inevitably leads to a Coulomb repulsive interaction between them. The size of that repulsion quantifies the strength of electron correlations in the system, which in turn can cause the electrons to become heavier and slower. It was recognized early on that electron correlations are important to the physics of FeSCs.
2
One manifestation of strong correlations is an electrical resistivity that exhibits so-called bad-metal behavior, characterized by an anomalously short electron mean free path at room temperature,
3
as described in figure
Figure 1.

The allure of linearity. In a typical metal, the temperature dependence of the resistivity
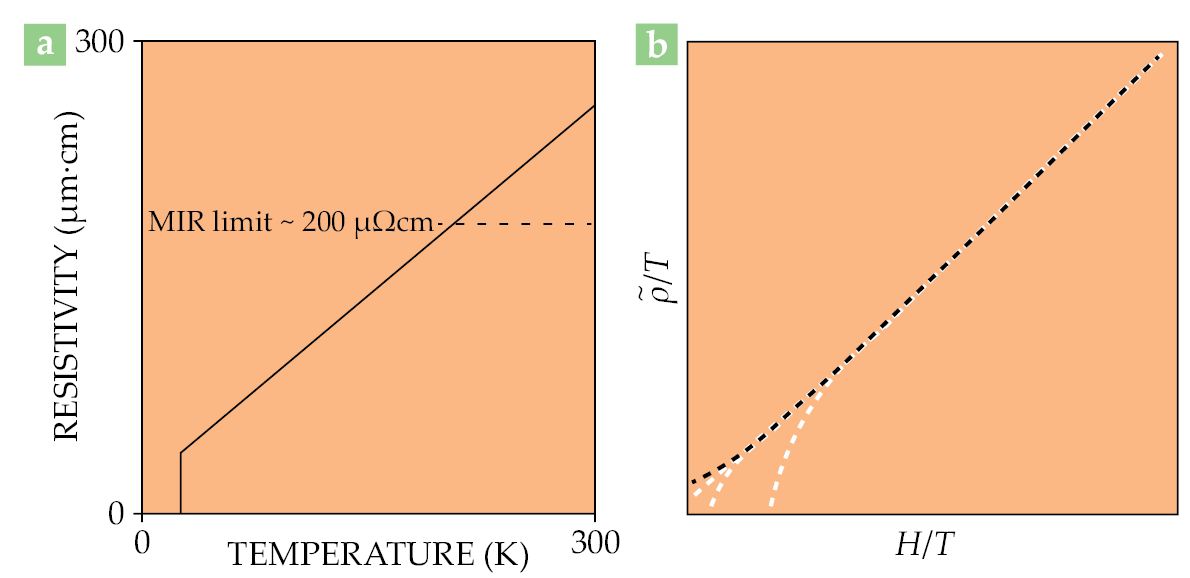
Accompanying evidence for that behavior comes from measurements of the optical conductivity and angle-resolved photoemission spectroscopy, 2 which show a significant renormalization of, among other parameters, the effective electron mass m∗ relative to its noninteracting counterpart mb. Remarkably, in FeSCs, that renormalization can even be orbital specific, with a mass enhancement m∗/mb that varies strongly from one orbital to another. In the Fe(Te, Se) series, m∗/mb in one of its 3d orbitals reaches almost 10 times that for the other 3d orbitals. 4 These observations further explicate the notion that electron correlations are strong in the FeSCs and motivate a new understanding about the nature of the superconducting pairing.
Theoretical treatments of the electron correlations in models that contain multiple 3d orbitals anticipated that orbital selectivity. One theoretical approach considers the system to be in the proximity of an orbital-selective Mott phase, where electrons within specific orbitals are localized on their respective lattice sites, while others remain itinerant, depending on the relative strength of the (unscreened) Coulomb repulsion (see figure
Figure 2.

Orbital-selective correlations among electrons. In a simple metal, conduction electrons are essentially free of interactions and readily propagate across the entire system like waves. But in iron-based superconductors, electrostatic repulsion between electrons primarily drives their superconductivity. The correlated electrons act as if only a fraction of them, Z, propagate freely. (a) That quasiparticle weight Zα is orbital dependent. It’s plotted for orbitals α = 3dxy and 3dxz/yz as a function of the on-site intra-orbital Coulomb repulsion U. Over an extended interaction range, the quasiparticle weight of the electrons in the 3dxy orbitals is much lower than those of the other orbitals. That regime is anchored by an orbital-selective Mott phase (OSMP), in which the 3dxy electrons are fully localized while the other orbitals have a nonzero quasiparticle (metallic) weight. (Adapted from ref.
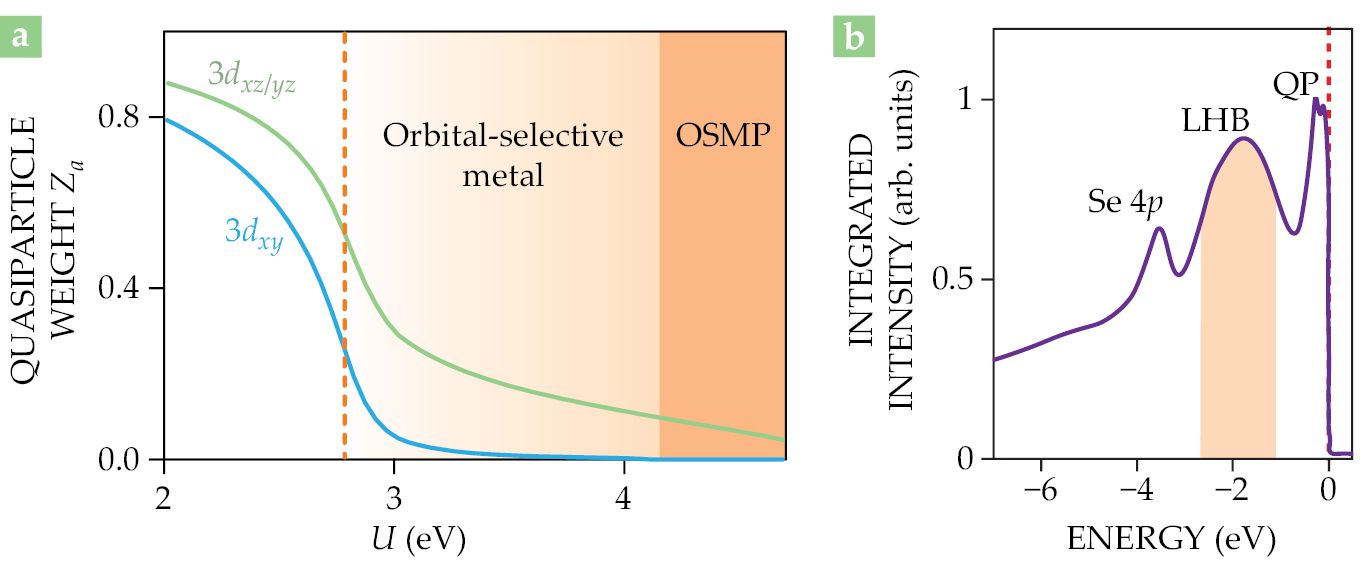
Because the dominant Coulomb repulsion is local, the electron dynamics are best captured in terms of short-range hopping between adjacent atomic sites rather than the usual metallic, wavelike propagation across the whole sample. Excitations between atomic energy levels split by the Coulomb repulsion can create an additional peak in the excitation spectrum. Observations of that additional “lower Hubbard band” peak, illustrated in figure
Electronic order and quantum criticality
Classical phase transitions in matter take place when the temperature is changed, as exemplified by ice melting or water evaporating. Quantum phase transitions, by contrast, occur at zero temperature and are induced by a change in the extent to which the Heisenberg uncertainty principle is manifest upon the variation of a nonthermal control parameter. Quantum criticality develops when the transition is continuous, and it controls the physics in a larger parameter regime at nonzero temperatures. (See the article by Subir Sachdev and Bernhard Keimer, Physics Today, February 2011, page 29
In the phase diagram of the iron pnictides, superconductivity adjoins an antiferromagnetically ordered phase in which the adjacent spins are anti-aligned along a specific direction.
2
By tuning a system appropriately, either through chemical substitution or by applying pressure, the phase transition to the magnetic state at the Néel temperature is suppressed to ever lower temperatures. Though superconductivity invariably intervenes, experimental signatures of mass renormalization imply that the magnetic phase terminates at a quantum critical point (QCP), where quantum fluctuations destroy the magnetic order, even at zero temperature (see box
Quantum criticality in iron pnictides—where all the players come together
Quantum criticality has been extensively studied in the iron pnictides. An early theoretical analysis by Jianhui Dai and coauthors 9 led to the proposal that isoelectronic phosphorus-for-arsenic substitution yields a quantum critical point, shown in panel a at a concentration x = xc. There, the antiferromagnetic (AF) and nematic (nem) orders vanish at the same time. Electronic nematicity describes the development of orientational symmetry breaking in the electronic phase and can be pictured by analogy with the anisotropy seen in the cosmic microwave background. As a result, both the magnetic and nematic degrees of freedom play a central role in creating critical quantum fluctuations (panel a) and in causing the effective carrier mass to diverge (panel b).

Researchers have now observed the concurrent quantum phase transitions in the P-substituted pnictides CeFeAsO and BaFe2As2. And in the BaFe2(As1−xPx)2 (and FeSe1-xSx) series, they demonstrated quantum criticality in multiple ways. Those include the extended T-linearity of the electrical resistivity inside the quantum critical fan (shown in panel a and on page 34 as the red zone) and an effective mass that diverges as the quantum critical point is approached from the paramagnetic side when the concentration exceeds xc (as indicated by the dashed black line in panel b and the intensity of yellow dots shown on page 34). 9 In the vicinity of the quantum critical point, the superconducting Tc is maximized (red solid curve in panel b). Thus, BaFe2(As1−xPx)2 provides a textbook example of superconductivity driven by the same critical quantum fluctuations that are responsible for the emergence of anomalous transport properties.
Earlier transport and thermodynamic measurements on isovalently substituted BaFe2(As1−xPx)2 provided strong evidence for mass renormalization due to the interaction of the itinerant carriers with quantum critical fluctuations of some underlying order parameter. 9
In addition to magnetic order, the iron pnictides also possess nematic order that spontaneously breaks the symmetry between the x and y spatial directions, setting in at or around the tetragonal-to-orthorhombic structural transition temperature TS. Figure
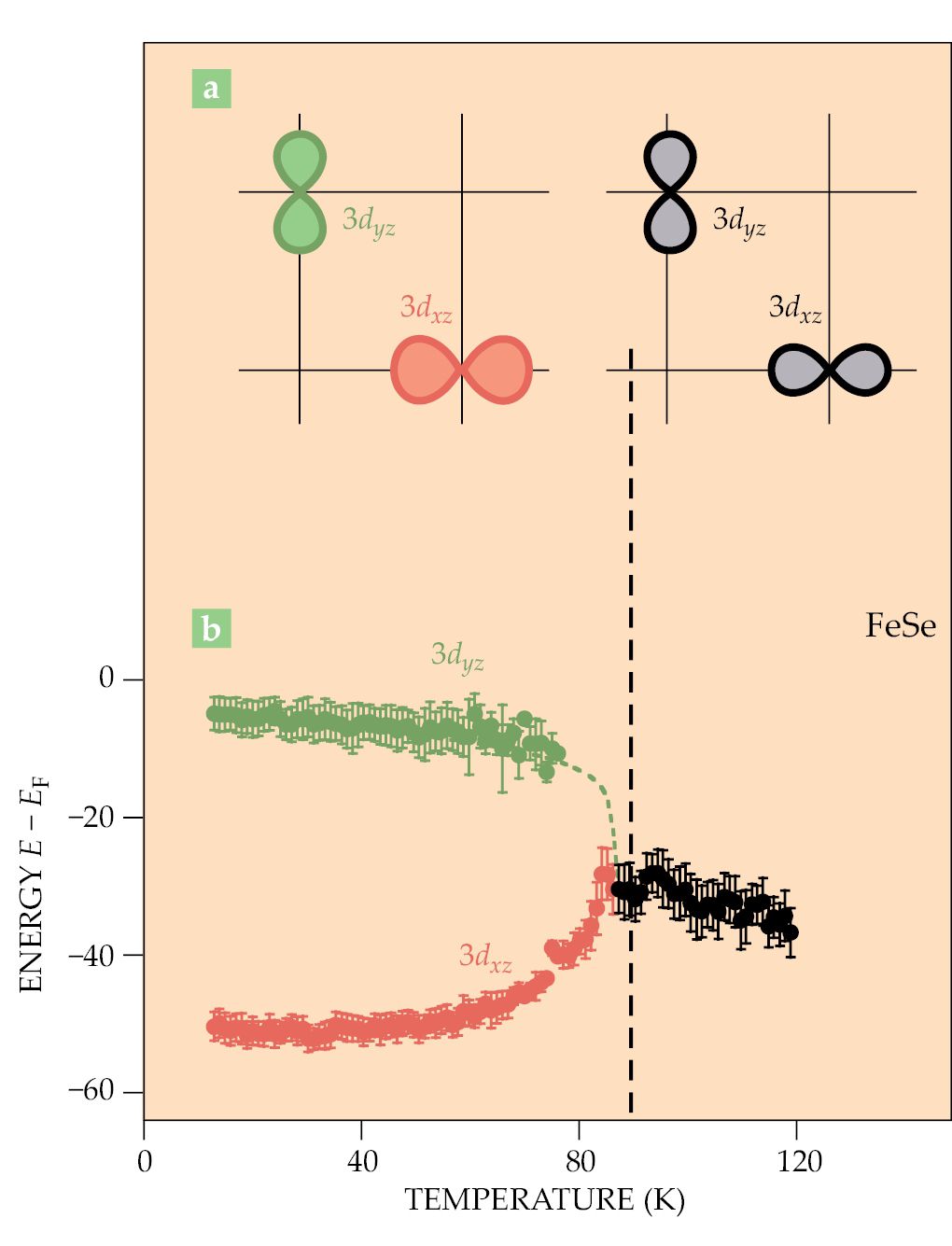
Figure 3.

Nematicity in iron selenide. (a) The breaking of the orbital degeneracy, shown schematically from right to left, is a proxy for the electronic nematic transition across a structural phase transition (vertical dashed line). The constituent ions of a crystal are arranged according to a geometric lattice, which provides a periodic potential for mobile electrons. The crystalline symmetry of FeSe dictates that its 3dxz and 3dyz orbitals (marked by different colors) can be transformed into each other by a 90° rotation in its tetragonal plane. That is indeed what happens when T > TS, the structural transition temperature. Upon FeSe’s cooling below TS, however, the symmetry is broken through the formation of an electronic nematic and is manifest as an inequivalence between the electronic bands associated with the 3dxz and 3dyz orbitals. (b) The 3dxz and 3dyz bands obtained from angle-resolved photoemission-spectroscopy measurements on detwinned FeSe show degenerate bands that are split as the temperature is lowered through the nematic transition. (Adapted from ref.
In many cases, the nematicity and magnetism appear to be strongly intertwined, as discussed in box
With increasing pressure, the critical nematic fluctuations in FeSe are quenched, presumably because of the emergence of long-range magnetic order before the nematic phase terminates. As mentioned earlier, Tc grows more than fourfold up to 40 K with increasing pressure, in tandem with the strengthening magnetic interactions. In sulfur-substituted FeSe, nematicity vanishes at a critical S concentration xc, at which point the nematic susceptibility, as deduced from elastoresistivity measurements, also diverges. 12 Since no magnetic order develops at any point at ambient pressure across the substitution series, the divergence hints at a pure nematic QCP in FeSe1−xSx.
One of the key experimental signatures of quantum criticality is an electrical resistivity displaying a marked linear temperature dependence down to low temperatures—well below the typical temperature scales associated with electron–phonon scattering, an example of which is shown in figure
In addition to that T-linear resistivity, magnetotransport studies on iron-based superconductors have uncovered a startling new feature of quantum-critical transport, namely a crossover to linear-in-field magnetoresistance in systems close to the QCP.
13
The particular scaling form of the magnetoresistance, shown in figure
Unconventional superconductivity
In the iron pnictides, the proximity of the superconducting phase to the static magnetic order suggests that the quantum fluctuations associated with the antiferromagnetic spin-exchange interactions are involved in the pairing mechanism. The same principle may apply to the iron chalcogenides. In the part of the phase diagram where superconductivity develops, the nature of the long-range electronic order differs from that seen in the iron pnictides, yet antiferromagnetic fluctuations are still prevalent. Although a smoking gun for nematic-fluctuation-assisted superconductivity remains elusive, superconductivity often emerges in FeSCs that exhibit quantum-critical nematic fluctuations.
In a conventional superconductor, the pairing function, or gap, is essentially isotropic in reciprocal space. For some of the pnictide superconductors, the Fermi surface comprises both electron pockets at the Brillouin-zone boundary and hole pockets at the zone center. Measurements largely support the notion that the pairing function actually changes sign across the electron and hole pockets while maintaining a fully gapped single-particle excitation spectrum, as predicted in a variety of theoretical studies. 2
But phase-sensitive measurements for the sign change remain difficult to interpret when other pairing channels are close in energy. For the highest-Tc group of iron chalcogenides, in which the Fermi surface contains only the electron pockets, researchers have reached similar conclusions regarding the pairing states and pairing amplitude. They suggest that the details of the Fermi surface are not as crucial as the effect of electron correlations.
The advent of orbital-selective correlations in the normal state naturally raises the question of its implications for the pairing amplitude, symmetry, and structure in the superconducting state. Indeed, such orbital-selective pairing has been visualized, in spectacular fashion, via tunneling measurements performed on the nematic FeSe (see figure
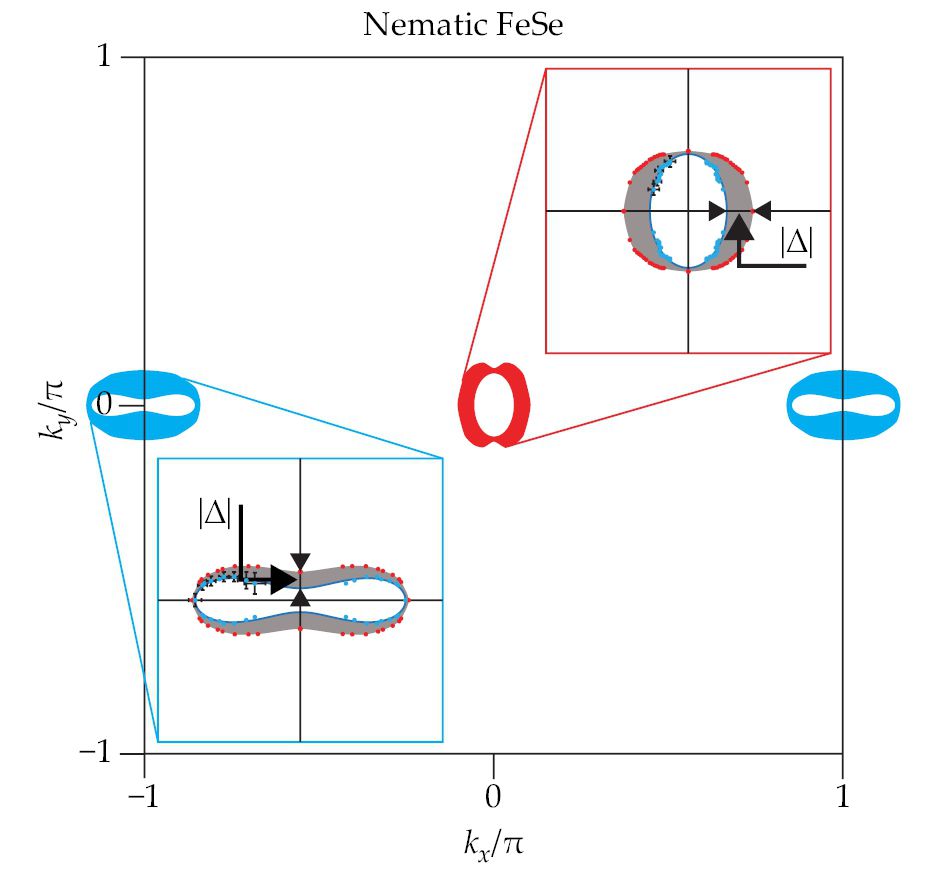
Figure 4.

Superconducting pairing from orbital-selective correlations. The variation of the superconducting gap magnitude |Δ| is shown on the hole Fermi pocket at the center (red, and top inset) and on the electron Fermi pocket at the side edges (blue, and bottom inset) of the Brillouin zone in iron selenide, as determined from scanning-tunneling-microscopy measurements. In a conventional phonon-mediated superconductor, the superconducting gap is essentially isotropic—that is, of the same magnitude over the entire Fermi surface. But in FeSe, the superconducting gap almost vanishes for specific momenta. Not only does such strong anisotropy hint at a nonphonon pairing mechanism, but it also illustrates how the different orbitals that contribute electronic states at the Fermi level can have very different pairing strengths. (Adapted from ref.
New horizons
Space restrictions inevitably prevent us from covering the whole gamut of exciting physics that is emerging from research into iron-based superconductors, such as the proximity of their superconducting state to Bose–Einstein condensation or the prospects for observing topological superconductivity at elevated temperatures. (With regard to the latter, the role of quantum critical fluctuations in enhancing the transition temperature points to an interesting and potentially profitable route to expand the domain of topological superconductivity.) Rather, in this final section, we consider the major impact that FeSCs are having in our efforts to understand a variety of other disparate families of unconventional superconductors.
Chief among these efforts is the guiding principle—so aptly demonstrated by the BaFe2(As1−xPx)2 series—that superconductivity is enhanced near a QCP. Those developments have solidified the idea that quantum critical fluctuations promote unconventional superconductivity and have led to the notion that orbital multiplicity allows for new types of Cooper pairing.
In that regard, developments in FeSCs have influenced investigations into other multiorbital superconductors. Although Sr2RuO4 has long been championed as a chiral spin-triplet superconductor, recent experiments suggest that it is a spin-singlet superconductor with an unusual pairing function (see Physics Today, September 2021, page 14
Another multiorbital superconductor, CeCu2Si2—the very first unconventional superconductor ever discovered—has long been thought to be nodeless. Recent experiments down to lower temperatures, however, have provided compelling evidence that the gap does not close anywhere on the Fermi surface, even though it is strongly anisotropic. The leading idea to resolve the conundrum invokes a multiorbital pairing state that is analogous to what has been proposed for the iron chalcogenides. 16 Multiorbital physics is now being actively investigated in a host of more recently discovered superconductors, including nickel-based compounds that represent a close structural cousin to the high-Tc cuprates—the exotic, heavy-fermion compound uranium telluride and the vanadium-based kagome metals.
Not only does nematicity provide a boon for tuning and probing unconventional superconductivity using uniaxial strain measurements, it also has encouraged the community to consider new pathways to improve superconducting performance. The essential argument is the following: Although the electron–phonon interaction acts on the entire Fermi surface, it is inherently weak. By contrast, antiferromagnetic interactions tend to be much stronger, but they only influence a restricted region in momentum space. In principle, nematicity offers the best of both worlds—strong interactions acting on the entire Fermi sea.
The challenge then is to harness those interactions either on their own or in conjunction with another pairing instability. At the same time, the success of engineered structures based on monolayer FeSe in raising Tc has provided an added incentive to achieve superconductivity in the purely two-dimensional limit. That frontier has enjoyed remarkable recent success with the discovery of superconductivity in monolayer tungsten telluride and twisted bilayer graphene, to name just two compounds.
One might even argue that the above effort has motivated other recent global attempts to realize superconductivity under extreme conditions, such as ultrahigh pressures for near-room-temperature superconductivity in the hydrides, or the realms of ultralow temperatures, where superconductivity is driven by quantum criticality in YbRh2Si2.
Given this rich vein of commonality, the time seems ripe for the development of a conceptual framework that unifies our understanding of such disparate material families of unconventional superconductors, with the precocious pnictides firmly at the helm. Ultimately, scientists would like to know how to achieve superconductivity with even higher transition temperatures at ambient conditions. Is there a design principle for boosting superconductivity? Our considerations in this article suggest the need for two central ingredients that cooperate with each other. One is for the entire Fermi surface to participate in promoting superconductivity. The other is to maximize the strength of the effective interactions that drive the superconductivity.
The band of unconventional superconductors to which FeSCs belong has the characteristic property that all electronic states are on the verge of localization and thus experience strong coupling. Compared with good metals, they also host stronger interactions that favor superconductivity. We envision that tuning the balance between interaction strength and localization is precisely the tool required to optimize superconductivity.
We thank Anna Böhmer, Lei Chen, Amalia Coldea, Pengcheng Dai, Ian Fisher, Frederic Hardy, Christoph Meingast, Matthew D. Watson, Ming Yi, Rong Yu, and Jian-Xin Zhu for their input. The work has been supported in part by the Theoretical Condensed Matter Physics program under the Department of Energy’s Basic Energy Sciences program and by the European Union’s Horizon 2020 research and innovation program, funded by the European Research Council.
References
1. Y. Kamihara et al., J. Am. Chem. Soc. 130, 3296 (2008). https://doi.org/10.1021/ja800073m
2. F. Wang, D.-H. Lee, Science 332, 200 (2011); https://doi.org/10.1126/science.1200182
D. J. Scalapino, Rev. Mod. Phys. 84, 1383 (2012); https://doi.org/10.1103/RevModPhys.84.1383
E. Dagotto, Rev. Mod. Phys. 85, 849 (2013); https://doi.org/10.1103/RevModPhys.85.849
P. Dai, Rev. Mod. Phys. 87, 855 (2015); https://doi.org/10.1103/RevModPhys.87.855
Q. Si, R. Yu, E. Abrahams, Nat. Rev. Mater. 1, 16017 (2016). https://doi.org/10.1038/natrevmats.2016.173. N. E. Hussey, K. Takenaka, H. Takagi, Philos. Mag. 84, 2847 (2004). https://doi.org/10.1080/14786430410001716944
4. J. Huang et al., Commun. Phys. 5, 29 (2022). https://doi.org/10.1038/s42005-022-00805-6
5. R. Yu et al., Front. Phys. 9, 578347 (2021) and references therein; https://doi.org/10.3389/fphy.2021.578347
M. Aichhorn et al., Phys. Rev. B 82, 064504 (2010); https://doi.org/10.1103/PhysRevB.82.064504
L. de’ Medici, G. Giovannetti, M. Capone, Phys. Rev. Lett. 112, 177001 (2014); https://doi.org/10.1103/PhysRevLett.112.177001
N. D. Patel et al., Commun. Phys. 2, 64 (2019). https://doi.org/10.1038/s42005-019-0155-36. T.-H. Lee et al., Phys. Rev. Lett. 121, 187003 (2018). https://doi.org/10.1103/PhysRevLett.121.187003
7. M. D. Watson et al., Phys. Rev. B 95, 081106(R) (2017). https://doi.org/10.1103/PhysRevB.95.081106
8. A. Kreisel, B. M. Andersen, P. J. Hirschfeld, Phys. Rev. B 98, 214518 (2018); https://doi.org/10.1103/PhysRevB.98.214518
R.-Q. Xing et al., Phys. Rev. B 95, 085108 (2017). https://doi.org/10.1103/PhysRevB.95.0851089. T. Shibauchi, A. Carrington, Y. Matsuda, Annu. Rev. Condens. Matter Phys. 5, 113 (2014) and references therein; https://doi.org/10.1146/annurev-conmatphys-031113-133921
J. Dai et al., Proc. Natl. Acad. Sci. USA 106, 4118 (2009). https://doi.org/10.1073/pnas.090088610610. T. Worasaran et al., Science 372, 973 (2021); https://doi.org/10.1126/science.abb9280
P. Malinowski et al., Nat. Phys. 16, 1189 (2020). https://doi.org/10.1038/s41567-020-0983-911. S. Lederer et al., Phys. Rev. Lett. 114, 097001 (2015). https://doi.org/10.1103/PhysRevLett.114.097001
12. S. Hosoi et al., Proc. Natl. Acad. Sci. USA 113, 8139 (2016); https://doi.org/10.1073/pnas.1605806113
S. Licciardello et al., Nature 567, 213 (2019); https://doi.org/10.1038/s41586-019-0923-y
S. Licciardello et al., Phys. Rev. Res. 1, 023011 (2019). https://doi.org/10.1103/PhysRevResearch.1.02301113. I. Hayes et al., Nat. Phys. 12, 916 (2016); https://doi.org/10.1038/nphys3773
S. Kasahara et al., Phys. Rev. B 81, 184519 (2010). https://doi.org/10.1103/PhysRevB.81.18451914. P. O. Sprau et al., Science 357, 75 (2017). https://doi.org/10.1126/science.aal1575
15. L. Benfatto, B. Valenzuela, L. Fanfarillo, npj Quantum Mater. 3, 56 (2018); https://doi.org/10.1038/s41535-018-0129-9
H. Hu et al., Phys. Rev. B 98, 220503(R) (2018). https://doi.org/10.1103/PhysRevB.98.22050316. R. Yu, J.-X. Zhu, Q. Si, Phys. Rev. B 89, 024509 (2014); https://doi.org/10.1103/PhysRevB.89.024509
T. Ong, P. Coleman, J. Schmalian, Proc. Nat. Acad. Sci. USA 113, 5486 (2016); https://doi.org/10.1073/pnas.1523064113
M. Smidman et al., Philos. Mag. 98, 2930 (2018). https://doi.org/10.1080/14786435.2018.151107017. M. Yi et al., Phys. Rev. X 9, 041049 (2019); https://doi.org/10.1103/PhysRevX.9.041049
A. E. Böhmer et al., Phys. Rev. Lett. 114, 027001 (2015). https://doi.org/10.1103/PhysRevLett.114.027001
More about the authors
Qimiao Si (qmsi@rice.edu






