In celebration of Ilya Lifshitz

Virtually every physicist has encountered the famous Landau and Lifshitz textbooks, but many may not know that there were two Lifshitz brothers, both physicists. The textbook Lifshitz is the older, Evgeny Lifshitz (1915–85); this article concerns the younger, Ilya Lifshitz (1917–82), shown in figure 1 as a young man. Their parents were Mikhail Lifshitz, a physician, and Berta. Mikhail was from a poor Jewish family that lived in the Pale of Settlement in tsarist Russia. He received his medical education in Heidelberg, Germany, where he won a gold medal for student research and, according to family legend, was presented to Queen Victoria as one of the best European medical students. As was traditional in such families, Evgeny and Ilya received a sound early education at home. Evgeny excelled in languages; Ilya was proficient in music.

Figure 1.

The family lived in Kharkov, Ukraine, a cultural and industrial center that was also becoming a notable science hub. The Ukrainian Institute of Physics and Technology (UPTI), founded there in 1930, attracted visits from the likes of Niels Bohr and Paul Ehrenfest. In 1932, fresh from his 18-month stay in Europe, Lev Landau arrived in Kharkov to lead the theoretical division at UPTI and, simultaneously, to take up a chair in theoretical physics at Kharkov’s Mechanical Engineering Institute.

The following year, Ilya became a physics student at the Mechanical Engineering Institute. In parallel, he studied pure mathematics at Kharkov University, whose faculty included several first-rate mathematicians. Ilya also studied music at the Kharkov Conservatory. Though he never completed the program, he took great pleasure in playing piano at home for his family and friends. Much later he took up stamp collecting as a hobby and achieved an international reputation.

Always independent, Ilya carried out his PhD work without an adviser; he would later emphasize tactfully that although Landau was a hugely beneficial influence, he had never been Landau’s student. In light of that, Landau’s Moscow disciples jokingly called Ilya an appanage prince, referring to the younger members of a royal family who are given a small portion of the kingdom to provide income until they inherit a more important position. Nevertheless, on Landau’s death in 1968, it was Ilya who became his successor as head of Moscow’s prestigious theoretical division in the P. L. Kapitza Institute for Physical Problems. Thus, for the last 14 years of his life, Ilya worked next door to his older brother.

A man of deep decency

Ilya and Evgeny shared a devotion to science, but in many ways they were very different. Meticulously dressed, efficient, lean, and unsmiling, Evgeny hardly ever supervised graduate students. By contrast, Ilya was stouter and radiated friendliness; students, colleagues, and collaborators seemed unable to resist his charm. When he taught or delivered a seminar, his enthusiasm was infectious. Excited, he could easily forget his somewhat old-fashioned manners: Once, when trying to explain knots in DNA to a large audience, he theatrically removed the belt from his trousers. ¹ Even in later life, after he had received many honors, Ilya was almost childishly excited about any discovery—his or someone else’s—that showed intellectual beauty. In his office, one met mathematicians, polymer chemists, and biophysicists besides the usual theoretical and experimental physicists.

Ilya had harmonious relationships with his students. He worked individually with each and was sensitive to the moment when one was mature enough to become independent. Often, he would take a few students and start a new research direction; his colleagues would shrug their shoulders and ask, “Why metals?” When, after some years, those students had become renowned authorities in their still-fertile field, Ilya would suddenly abandon it, take a few new students, and jump into something entirely different. Yet again there would be muttering: “Why polymers?”

In the USSR of those days, it was impossible to hide from difficult interactions with the authorities. Neither Lifshitz was an open dissident, but each refused to tarnish himself with a morally questionable act. For instance, during a press campaign accusing Andrei Sakharov of anti-Sovietism, senior scientists came under enormous pressure to sign condemnatory letters. Many did, but not the Lifshitzes. When Mark Azbel, one of Ilya’s outstanding disciples, became a refusenik—that is, the authorities refused to permit his emigration—many colleagues were afraid even to talk to him. But not Ilya. One of us (Grosberg) witnessed how Mark stood alone in the lobby of a Moscow seminar room, with no one approaching him, until Ilya entered and, with his friendly smile, started a conversation. He was not a hero; he was just a man of a deep decency—and that’s not insignificant in a totalitarian state.

Ilya did not aim to climb high on the administrative ladder, but he did receive the highest scientific distinctions in the USSR. He was particularly proud to be elected a member of the Soviet Academy of Sciences in 1970; he explained privately that voting for academy membership was the only secret ballot in the country. Neither his academic title nor the tremendous reputation he enjoyed among his colleagues protected him from disappointing treatment by administrators; the many bitter setbacks he endured ranged from issues of student recruitment and employment to the leadership of his departments at Moscow State University.

Having described the man, we now turn to three of his scientific achievements.

Fermiology

Rudolf Peierls told one of us (Singleton) that Ilya Lifshitz was the person who defined a metal as “a solid with a Fermi surface,” even though others set those words down in print first. ² Be that as it may, Lifshitz and collaborators certainly expressed themselves memorably on the subject. For example, in a paper with Moisei Kaganov he wrote, “Each metal acquired its own ‘face’. . . . its Fermi surface, a ‘visiting card’ describing the constant-energy surface which at zero temperature separates the occupied from the empty states in quasi-momentum space.” ³ The reference to the constant-energy surface is the definition of the Fermi surface that we nowadays teach to students. The earlier part of the quote refers to one of Lifshitz’s major achievements—a model that, for the first time, allowed three-dimensional Fermi-surface shapes to be deduced from experimental observations. ⁴

Why is the Fermi surface important? To quote Lifshitz and Kaganov again, it is “the stage on which the ‘drama of the life of the electron’ is played out.” ² The Fermi surface is the only place in k space where filled and empty states are adjacent (k is the quasi-momentum mentioned above, the conserved quantity that replaces momentum for a particle in a spatially periodic potential). As such, it determines all of a metal’s properties. A knowledge of the Fermi surface—the goal of fermiology—enables one to check band-structure models and to understand most of the mechanical, electrical, and magnetic properties of a metal. ^{2 , 4 , 5}

Lifshitz’s interest in fermiology came via Landau. In 1930, soon after Arnold Sommerfeld successfully applied quantum statistics to the theory of metals, Landau famously predicted diamagnetism due to the orbital motion of band electrons. His paper contains a laconic statement about magnetization oscillations that are periodic in 1/(magnetic field), a phenomenon now known as the de Haas–van Alphen (dHvA) effect. Landau, however, dismissed the effect as unobservable under the experimental field strength and homogeneity then available. He was certainly correct for most metals, but ironically, just a few weeks after his paper appeared, Wander de Haas and Pieter van Alphen reported their first experimental observations of magnetization oscillations in the semimetal bismuth. ⁴

The Hamiltonian of an electron in a magnetic field can be solved analytically only for a Fermi surface that is a sphere or an ellipsoid of rotation; that was the approach followed by Peierls, Landau, and others during the 1930s to analyze increasingly sophisticated dHvA experiments on bismuth. However, bismuth is a special case, a semimetal with a simple Fermi surface consisting of four tiny, ellipsoidal pockets. The small pocket size causes widely spaced dHvA oscillations, so field inhomogeneities are not worrisome. The ellipsoidal shape gives rise to an easily understood dependence of the oscillations on the orientation of the field with respect to the crystal axes.

After World War II and its interruption of further investigations, it came as something of a surprise when a succession of true metals exhibited a plethora of dHvA oscillations with much more complex field-orientation dependences. The ellipsoidal-surface model was inadequate to explain those data, which demanded a theory for the quantum mechanics of electrons on an arbitrarily shaped Fermi surface exposed to a magnetic field.

Fantasies of a modern artist

Lifshitz’s insight was to apply Bohr’s correspondence principle to closed electron orbits on the Fermi surface in a magnetic field—that is, to assume that the difference in energy of adjacent levels is ℏ times the angular frequency of the corresponding classical motion. The frequency at which electrons orbit, known as the cyclotron frequency, is proportional to the field; it determines the separation of the electrons’ energy levels, now called Landau levels (LLs). Each closed orbit about the Fermi surface (see figure 2a) will have its own set of LLs, but it turns out that the LLs associated with extremal orbits dominate the response of the metal.

Figure 2.

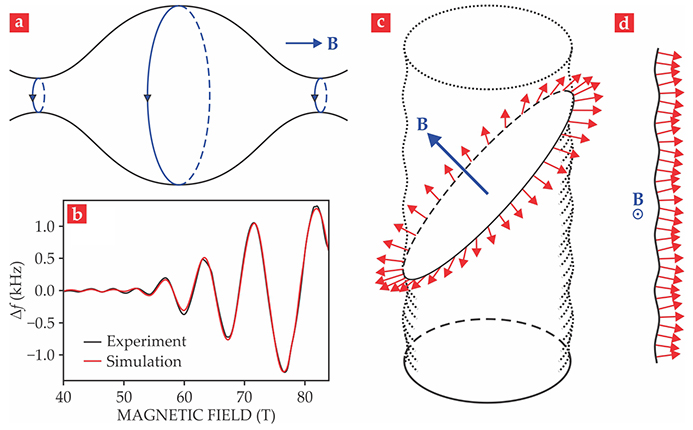
Because the LL spacing is proportional to the magnetic field, an increase in the field causes LLs to successively approach, pass through, and exit the Fermi surface as their energies rise above the surface’s energy—the Fermi energy. The field increase thus modulates the density of states at the Fermi energy and causes the metal’s properties, including magnetization, to oscillate. Each extremal orbit contributes a series of such oscillations (see figure 2b).

The correspondence principle is only valid for large quantum numbers. But Lifshitz realized that it always applied to conventional metals in the experimental fields of the time, which even in pulsed magnets rarely exceeded 10 T. Proceeding from that premise, he found that the inverse of the periodicity of each series of dHvA oscillations is proportional to the corresponding extremal cross-sectional area of the Fermi surface in the plane perpendicular to the magnetic field. (Figure 2a shows the geometry.) Consequently, dHvA data in which the field is applied at various angles to a crystal could be used to map the 3D Fermi-surface shape. Lifshitz described the idea in a seminar in 1950; Lars Onsager independently published similar conclusions in 1952. With Arnold Kosevich, Lifshitz further developed the theory to take into account temperature and impurity scattering. Their Lifshitz–Kosevich formula enables the extraction of such electronic parameters as effective masses, g factors, and scattering rates.

Lifshitz and coworkers then studied how a metal’s resistivity in a magnetic field depends on the kinetics of electrons at the Fermi surface. They analyzed the Shubnikov–de Haas (SdH) effect—resistivity oscillations analogous to dHvA oscillations in magnetization. They also showed that the field-orientation dependence of various components of a metal’s resistivity tensor could be used to map out details of the Fermi surface, an observation that follows from the fact that trajectories on the surface can be closed or open, as illustrated in figures 2c and 2d.

Even today, dHvA and SdH oscillations are experimental tools of choice for studying many aspects of metals. They are applied to substances as diverse as heavy-fermion compounds, whose novel properties derive from partially filled f orbitals of rare-earth or actinide ions, cuprate semiconductors, and crystalline organic conductors. All those and more are now regarded as metals because they possess Fermi surfaces.

This introduction to fermiology concludes with a hot topic in condensed-matter physics: changes in the topology of a Fermi surface, or Lifshitz transitions. If a metal is subject to pressure, to give one example, a Fermi-surface section such as that shown in figure 2a may constrict so much that the narrow necks disappear. At that instant, the Fermi-surface topology changes from an extended object to a series of isolated pockets. Lifshitz transitions are thought to be important in many areas of physics, including high-temperature superconductivity, topological insulators and other topological materials, and even black holes. ⁶

Lifshitz was modest about his pivotal contributions to fermiology. He likened the increasingly exotic Fermi surfaces extracted from his insights to the fantasies of a modern artist. It was a prophetic description. The Fermi surface of lead inspired the sculpture shown on page 45: For Dolores (Flores para los muertos), by Tony Smith. ²

Disordered systems

Lifshitz published his first paper on disordered systems when he was only 20 years old. It was an analysis of the diffuse scattering of x rays due to defects in a crystalline lattice. Soon afterward, he turned to the impact of defects on absorption and refraction of IR radiation. ⁷ Since an IR wavelength is very large compared with the atomic spacing in a crystal, Lifshitz analyzed the problem in terms of the coupling of vibrational modes to a uniform electric field that oscillates at the IR frequency.

For a lattice without disorder, IR radiation can be absorbed only if the incident photons are matched to the frequency of a vibrational mode with quasi-momentum k = 0. Below each absorption frequency is a finite frequency band for which incident radiation will be totally reflected at the crystal surface. For frequencies outside the bands of total reflection, a fraction of the incident power will be transmitted into the crystal and propagate without absorption.

The situation is qualitatively different for a crystal with disorder. Because the disorder allows momentum to be freely transferred to the lattice, the energy of an incident photon can be transferred to any phonon with a matching frequency, regardless of the phonon’s k. Consequently, radiation of any frequency within the range covered by the entire set of the crystal’s phonons will have a finite absorption length. In addition, defects can lead to localized vibrational modes outside the frequency range of the perfect crystal; IR radiation with frequencies matched to those extra modes will also be absorbed.

Lifshitz tails

Many of the effects of disorder on vibrational modes have parallels in the theory of electronic states in a disordered system. Hence, Lifshitz was naturally interested. His most famous contribution was his 1964 description of what are commonly referred to as Lifshitz tails, regions of energy in which the electron density of states might be expected to be zero but is actually nonzero because of rare fluctuations in the local density of impurities. ⁸

As a simple example, consider a model in which space is divided into cubic cells with sides of length $a$. Within any cell, the potential $V$ is constant and takes on one of two values: Either $V=U$, with probability $p$, or $V=0$, with probability $1-p$ (see figure 3a). If $p$ is small, one can think of the cells with $V=0$ as the host crystal and the remaining cells as impurities. The issue to be addressed is the density of states at low energies for a quantum particle of mass $m$ moving in the potential $V$. Suppose that $\left|U\right|$ is very small compared with ${\hslash }^2/{ma}^2$, an expression that estimates the kinetic energy $E_{\mathrm{K}}$ paid to confine the mass to a single cell. In that case, a low-energy particle would not be sensitive to the potential in any one lattice cell but would instead respond to the potential averaged over a region containing many cells.

Figure 3.

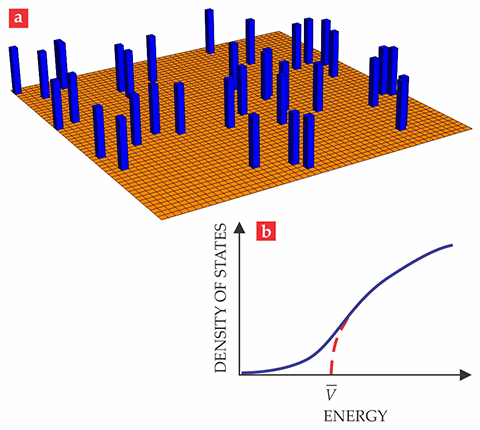
To a first approximation, the particle would behave as though it were moving in a uniform potential equal to the average potential in the crystal, $\bar{V}=pU$. The density of states would thus be zero for energies $E$ less than $\bar{V}$ and otherwise would be that of a free particle, proportional to ${(E-\bar{V})}^{1/2}$.

In reality, however, there will always be states with energies less than $\bar{V}$. For example, if $U$ is positive (and thus so is $\bar{V}$), the lower bound to the energy spectrum will actually be at $E=0$. After all, statistical fluctuations guarantee that an infinite sample will have impurity-free regions of arbitrarily large size, and a particle confined to a sufficiently large empty region can have an energy arbitrarily close to zero. For a spherical region of radius $R$ without impurities, there must exist at least one electronic state that is localized in the region and that has an energy $E$ equal to or less than a value on the order of $E_{\mathrm{K}}{a}^2/R^2$. The probability $P$ that a region of radius $R$ actually is devoid of impurities is given by $P={(1-p)}^N$, where $N$ is the volume of the sphere in units of $a^3$. Noting that $N\propto R^3\propto E^{-3/2}$, one obtains in the limit of small $E$ a rough estimate for the number of energy states per unit volume with energy less than $E:exp[-p{(E_0/E)}_{3/2}]$, where $E_0$ is on the order of $E_{\mathrm{K}}$. The analysis for the case $U<0$ proceeds similarly, but the bottom of the energy band is at $U$ rather than 0.

Figure 3b shows the low-energy density of states according to the argument just sketched. A more careful analysis reveals that the most probable spherical region for confining a state of low energy is not completely devoid of impurities but instead contains a small residual density that depends on $E$ and $U/E_{\mathrm{K}}$. Further refinements take into account fluctuations about the optimal distribution of impurities. Those improvements lead to a more accurate value of the parameter $E_0$ and to better estimates of the preexponential factor in the density of states, but do not affect the overall conclusion that the density of states has an exponentially falling tail at energies below $\bar{V}$. In his 1964 paper, ⁸ Lifshitz used extensions of the above reasoning to estimate the density of states in the entire region between the bottom of the energy band and the mean potential $\bar{V}$ for both positive and negative $U$.

The concept of Lifshitz tails has influenced thinking in several fields. Lifshitz tails have been invoked, for example, in discussions of electron mobility in disordered systems and of optical absorption at frequencies below the threshold that would exist for a perfect crystal. Related concepts have been used to describe peculiar phases of disordered magnetic and ferroelectric systems. ⁹

Polymers and biophysics

In the mid 1960s, Lifshitz shifted his interest to polymers, which were also attracting the attention of Samuel Edwards and Pierre-Gilles de Gennes. The three revolutionized the way physicists think about polymers and in the process spawned the field of soft condensed-matter physics. However, their paths to polymers were very different. Interested in chemical engineering applications, Edwards was attracted by gelation and rubber elasticity, whereas de Gennes famously recognized a mathematical mapping between polymers and a particular limit of critical phenomena. By contrast, Lifshitz (shown later in his career in figure 4) came to polymers from biophysics—not a trivial point given that in the USSR of the 1960s, any involvement in modern biology had a clear flavor of political disobedience. Excited by the initial discoveries of molecular biology, Lifshitz was the first to recognize the connection between biopolymers and disordered systems.

Figure 4.

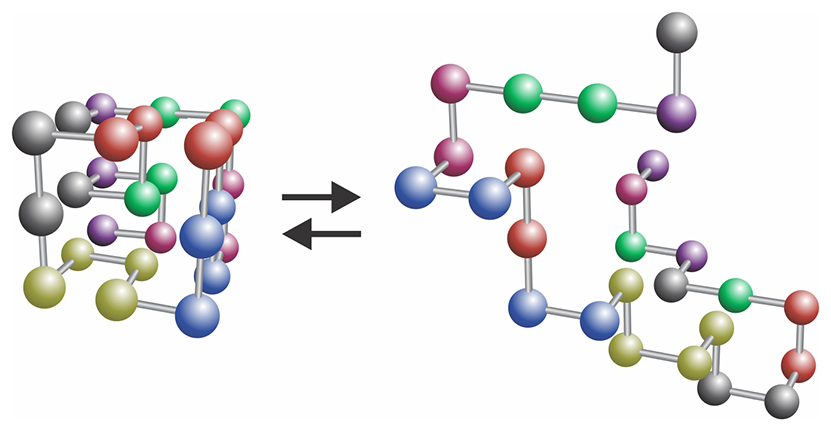
Based on that connection, Lifshitz’s main contribution to polymer physics is the theory of the coil–globule phase transition, also called polymer collapse (see figure 5). That a concept such as a phase transition can be applied to a single molecule is not obvious; even the longest polymer chains have nowhere near the number of particles found in conventional macroscopic systems. Nevertheless, polymer collapse is a phase transition in the sense that the width of the ambiguous zone separating the fluffy fluctuating coil from the dense liquid-like globule systematically decreases as the chain length increases. The coil–globule transition is, in most cases, very smooth—an almost pure second-order transition. However, the presence of surface energy makes the transition weakly first order, one that produces a small latent heat proportional to the surface area of the globule rather than to the number of particles in the chain.

Figure 5.

To approach the equilibrium statistical mechanics of polymer globules, Lifshitz assumed that a chain link at spatial point $x$ feels an external potential $U(x)$. He then considered the partition sum over all spatial conformations of a chain and noticed that the sum was mathematically similar to the Feynman path integral for a quantum particle moving in a potential proportional to $U(x)/k_{\mathrm{B}}T$, with $k_{\mathrm{B}}$ being Boltzmann’s constant and $T$ the temperature; Edwards had independently reached the same conclusion.

Unlike Edwards, however, Lifshitz paid attention to the corresponding Schrödinger equation. In that context, when $U(x)$ is a potential well, the effective potential $U(x)/k_{\mathrm{B}}T$ becomes deeper as the temperature decreases. Lifshitz elegantly interpreted the simplest coil–globule transition as occurring at the temperature at which the discrete ground-state energy level splits from the lower border of the continuous spectrum. Indeed, the discrete-level wavefunction corresponds to the globule form of the polymer chain, confined within the potential well. Lifshitz’s theory is quite a contrast to the critical-phenomena concepts developed simultaneously, mostly by the de Gennes group, and it was initially received with skepticism. The controversy was fruitful, as its resolution brought forth an understanding of where the critical-phenomena and mean-field approaches were applicable.

Another interesting controversy arose in the early to mid 1970s, when the Lifshitz theory, with its predicted almost-second-order transition, was compared with experiments on protein globules. At the time, Lifshitz and others thought of the denaturation and renaturation as the globules’ unfolding and refolding and viewed those processes as coil–globule transitions par excellence. But the experiments showed that the transitions produced a large latent heat, comparable per particle to that observed in the melting of regular molecular crystals. The first explanation was rather dismissive: The Lifshitz theory was for homopolymers consisting of a single monomer species, whereas proteins are obviously heteropolymers. Such a discouraging conclusion could be justified from Lifshitz’s papers, which addressed homopolymers only. But in seminars that , unfortunately, were not presented anywhere outside the USSR, more generally applicable arguments were discussed and honed.

Years later Lifshitz’s ideas bore fruit in biophysics, once it was understood that the first-order nature of coil–globule transitions in proteins is a property of particular amino-acid sequences. Theoretically, such sequences could be identified and created by computer or in real experiments via a process called sequence design. The new understanding permitted biophysicists to estimate the number of sequences exhibiting first-order folding transitions and led to the idea that such sequences have been selected by evolution for their stability against mutations and environmental perturbations. ^{10 , 11}

Lifshitz’s insights into polymer globules have also informed the now hot topic of genome folding. The puzzle is to understand how 2 m of DNA are housed and accessible in the 10 µm nucleus of every cell of the human body. ^12–14

Ahead of fashion

In a career spanning from the end of the 1930s to the start of the 1980s, Ilya Mikhailovich Lifshitz had a remarkable influence on the study of fermiology, disordered systems, and biophysics. He also made other contributions, no less impressive, some of which are among his most cited. Those include work with Vitaly Slezov on the kinetics of first-order phase transitions (including the famous t^1/3 law describing the growth of the nucleus of a new phase), a study with Alexander Andreev on quantum diffusion of vacancies, and an investigation of quantum-tunneling kinetics of nucleation with Yuri Kagan. Many times, when Lifshitz entered a field, he was not following fashion. But fashion often followed him, even if it sometimes took 20 years to catch up.

Supplemental material: A few personal memories of Ilya Lifshitz

Alexander Grosberg: I was fortunate to work closely with Ilya Mikhailovich for 13 years. As it turns out, however, I passed the most difficult exam when I first visited him in his home office. He treated me to a box of chocolates. When I took a second piece, he smiled and said, “It is my test! Good theorists like chocolate.”

Bertrand Halperin: I met Lifshitz on two occasions in Moscow. In 1971 and 1974 I was one of the youngest members of a delegation of American visitors. Lifshitz was very kind to me and invited me to lunch at the Academy of Sciences. I think he had a special affection for me, because in 1964 I had done work as a graduate student that had strong overlaps with his work on tails in the density of states. During the 1974 trip, I paid a visit to Mark Azbel, who had been excluded from our conference because he was a refusenik. After that, Lifshitz took me aside to let me know that he was very pleased with my action.

John Singleton: In gathering the information for our commemoration of Lifshitz, I was reminded of the high regard in which he was held by all of the senior physicists at Oxford and Cambridge Universities when I was a student in the 1980s. On hearing of his death, Rudolf Peierls, Betty and Brebis Bleaney, Nicholas Kurti, Nevill Mott, Mary O’Brien, Harry Rosenberg, and David Schoenberg spoke with nostalgia about his work, his correspondence with them, his thirst for new experimental data (and stamps!), and his encouragement.