High-energy-density physics
DOI: 10.1063/1.3455249
Matter whose energy density corresponds to pressures above about 1 million atmospheres behaves differently from the more familiar solid, liquid, gaseous, and plasma states. Instead, its properties and behavior overlap with systems known from astronomy and astrophysics—planetary interiors, stars, and the early universe.
To understand the interiors of planets, one must create and measure the behavior of matter at planetary pressures. To understand the structure of stars, one must create and measure the interactions between stellar matter and x-ray photons. To understand astrophysical explosions such as supernovae, one must create and measure the relevant dynamical processes. To understand strongly relativistic systems such as existed in the early universe, one must create and measure strongly relativistic interactions of matter and photons. In none of those areas is theory or simulation straightforward; validation of theoretical and numerical results requires benchmark measurements that offer the potential for novel discoveries. All the systems mentioned above are accessible, at least in some ways, to investigations in high-energy-density (HED) physics laboratories, whose studies promise to yield a host of practical applications in addition to fundamental science.
Origins and scope
Even some years into the 20th century, the highest densities known to humans were those of solid matter, and the highest temperatures were below 100 000 K. Early understanding of denser, hotter systems originated from three sources. The first was the quest by Arthur Eddington, Subrahmanyan Chandrasekhar, Martin Schwarzschild, and many others to understand stellar structure. 1 Their work eventually led to the understanding that stars release energy by nuclear fusion and that matter could exist at much higher densities and much hotter temperatures than previously assumed. The second source was the development of nuclear explosives. Richard Rhodes, for example, describes how difficult it was for the scientists of the Manhattan Project to grasp the idea that metals could be compressed; 2 that idea is now second nature to students in HED physics. In the mid-1960s, Yakov Zel’dovich and Yuri Raizer published their seminal book, which described the fundamental science of dense, hot systems as it was then understood. 3 The third source was the pursuit of inertially confined fusion, begun in the 1960s and declassified in 1972, the same year a key paper by John Nuckolls and others was published in Nature. 4
I date the emergence of HED physics to 1979. Ten years previously, physicists had assembled at a largely theoretical conference entitled “The Physics of High Energy Density.” 5 By 1979, facilities were becoming capable of performing a wide range of fundamental experiments, and the first user-facility program in HED physics was established at the Laboratory for Laser Energetics at the University of Rochester. Since then, a large number of user programs have been established in the US, Europe, and Asia, and the sophistication of the facilities and diagnostics has evolved rapidly. In addition, the entire field of relativistic HED physics, also known as high-field physics, was enabled by the invention in the early 1980s of so-called chirped-pulse amplification of laser light, a technique that generated laser electromagnetic fields of unprecedented intensities (see reference 6 and the article by Gérard Mourou, Christopher Barty, and Michael Perry in Physics Today, January 1998, page 22 ). The year 2006 saw the first book developed specifically as a graduate text for HED physics. 7
In 2003 a National Research Council committee defined the field of HED physics as the study of systems whose energy density corresponds to thermal pressures above 0.1 TPa (1 million atmospheres or 1 Mbar).
8
Such extraordinary conditions can be created by thermal pressure, internal energy of material constituents, intense fields, or a combination of those. Indeed, today’s experimental devices can heat solid-density matter to millions of degrees, can heat atmospheric-density matter to relativistic temperatures, and can perform and diagnose complex experiments under those conditions.
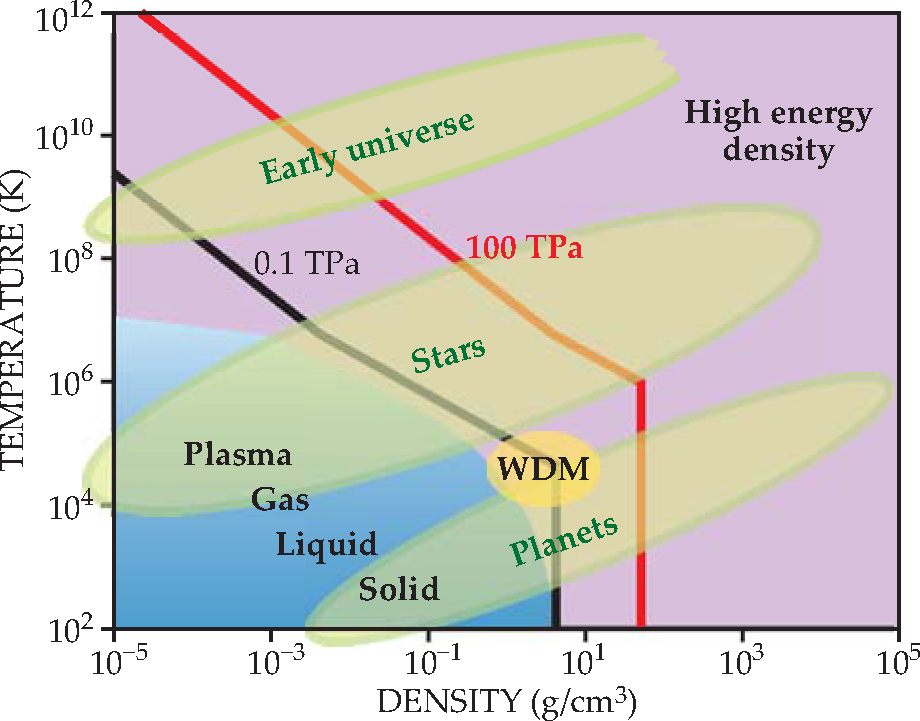
Figure 1 illustrates the HED regime and, in particular, shows its overlap with a number of systems known from astronomy and astrophysics. Solids, liquids, and gases persist to temperatures up to about 10 000 K and to densities up to a few times the density of nuclei in water, 1029 nuclei/m3; raising the temperature or density above those benchmark values frees electrons. The neutral states of matter continue off the plot in the figure downward and to the left. Traditional, ideal plasmas exist at low enough densities that the particles are weakly correlated. Once the pressure increases above 0.1 TPa or so, however, the system becomes an HED system. Depending on the specific values of temperature and density, one may need to consider particle correlations, electric and magnetic forces, or radiative, relativistic, or quantum mechanical effects;
Figure 1. Conventional and high-energy-density physics. According to a definition proposed in 2003 by the US National Research Council, an HED system is one for which the pressure exceeds 0.1 TPa (106 atmospheres). In this plot, the defining boundary is shown as a solid black curve, calculated for a simple model of aluminum; specific details of the 0.1-TPa boundary vary with material. The vertical portion of the line shows the density at which one needs 0.1 TPa to compress Al. (For comparison, the density of water at room temperature and pressure is 1 g/cm3.) The change in slope in the diagonal segment at a temperature slightly below 107 K indicates that the Al is fully ionized. The red curve indicates a 100-TPa pressure. The region corresponding to so-called warm dense matter (WDM) is becoming increasingly accessible to experiment. One can approach the WDM region from the solid, liquid, gas, plasma, or Fermi-degenerate state; no matter, the standard models all fail. Green shading approximately indicates the regions spanned by material found in planets, stars, and the early universe. Astrophysical HED systems beyond the range shown here include gamma-ray bursts, stars that are about to explode, and compact objects such as neutron stars. Many astrophysical systems have dynamical features that can be studied in HED experiments. Those aspects relate to radiating shocks, relativistic dynamics, plasma hydrodynamics, and effects of extreme magnetic fields, among others.
Facilities that create high-energy-density conditions
The images shown here are from four facilities that produce high-energy-density (HED) matter. At the upper left and on the cover are open-shutter images from the University of Rochester’s Omega laser facility. Omega, which can pack 30 kJ of laser energy in a nanosecond-scale pulse or generate kJ pulses of much shorter duration, is one of several active kJ-class user facilities that provide a wide range of laser and diagnostic capabilities. The central region of the photo here shows glowing material heated by UV laser irradiation. The residual green light produced by the laser but not focused on the target illuminates the many structures used to hold experimental components and diagnostics. The entire region shown is about 1 m across; the target is 1 mm across. (Courtesy of Eugene Kowaluk.)
The photo at the upper right shows the Z pulsedpower device at Sandia National Laboratories. The facility uses magnetic forces driven by currents of tens of mega-amps to implode a shell of conducting material. The imploding shell takes about 100 ns to reach its axis, where it deposits many megajoules of concentrated energy. When Z fires, residual arcs above the pulse compression hardware produce a dramatic display. Numerous smaller-scale pulsed-power devices use mega-amp currents to produce and study states of matter created by intense currents and magnetic acceleration. The red barrier encircles a region about 5 m across; the Z device focuses its energy on a target about 1 cm in diameter. (Courtesy of Sandia National Laboratories.)
The lower right image shows key parts of the HERCULES laser, in operation at the University of Michigan. That laser, the most intense in the world, is entirely contained in an ordinary laboratory whose area is about 100 m2. The laser uses several joules of energy to produce a 30-fs pulse with an intensity of 1026 W/m2 focused on a micron-sized spot. Its intense light causes electrons to oscillate with a quiver momentum of about 100 mc, where m is the electron’s rest mass and c is the speed of light. Many smaller high-field lasers are probing the behavior of matter at relativistic conditions. (Courtesy of Anatoly Maksimchuk.)
The picture at the lower left shows the target bay of the National Ignition Facility at Lawrence Livermore National Laboratory, which houses by far the largest and highest-energy laser in the world. The goal of facilities such as NIF is to assemble a large enough quantity of HED matter to produce fusion ignition. The facilities concentrate more than a megajoule of energy in a pulse whose duration is 10 ns or so. NIF is operating today; similar facilities are being built in Europe and Asia. The target bay is about 10 m across; the NIF fusion targets have a diameter of a few millimeters. (Courtesy of Lawrence Livermore National Laboratory.)
The images shown here by no means give a complete roster of the ways in which high-energy conditions can be created. X-ray lasers such as the Linac Coherent Light Source at Stanford University can directly heat matter into an HED state. Pulsed-power devices such as Z can accelerate plates of material that produce high pressure upon impact with a target. The technique originated with gas guns that enabled matter to reach the low-pressure part of the HED regime; diamond anvil cells can reach that regime too. Particle accelerators often produce HED conditions within their bunches of accelerated particles. Heavy-ion accelerators such as the second-generation Neutralized Drift Compression Experiment at Lawrence Berkeley National Laboratory will be able to heat targets into the warm-dense-matter regime. The plans for the next major heavy-ion accelerator, the Facility for Antiproton and Ion Research at GSI in Germany, include an area for studies of HED physics.
The HED regime extends, in principle, to indefinitely high temperature and energy density. In particular, a distinct class of laboratory HED systems—quark-gluon plasmas, produced by colliding relativistic heavy ions—exists at densities far greater than those indicated in figure 1 (see the article by Barbara Jacak and Peter Steinberg in Physics Today, May 2010, page 39 ). They form at a temperature near 1012 K, and their energy density, of order 1 GeV/fm3, corresponds to a mass density some 1015 times that of water. At such densities, the particles interact primarily through the strong force. Challenges in the study of quark-gluon plasmas include producing them and demonstrating that they exist, measuring their properties, and elucidating their connections with other plasmas.
For many HED systems, the energy density is not primarily thermal. Those systems, which include strong magnetic fields, intense laser fields, intense x-ray radiation, and particle beams, are not easily depicted on plots such as that of figure 1. To give a couple of specifics, an electron or positron beam whose kinetic energy times current density exceeds 30 GeV × 100 kA/cm2 is considered to have a high energy density. Strong magnetic fields arise throughout HED physics because dense, ionized matter can carry intense electric currents. Today’s experiments produce magnetic fields up to 105 tesla (109 gauss). Fields just a bit stronger would have a pronounced impact on atomic structure and would need to be taken into account, for example, to interpret spectra from pulsar atmospheres and similar environments.
A shocking controversy
The properties of hydrogen significantly affect the structure of giant-planet interiors; understanding those properties is thus essential to resolving basic questions about planetary formation. 9 Nowadays, the uncertainties in hydrogen properties are so great that scientists don’t even know whether Jupiter has a core of ice and rock. Laboratory studies can reduce those uncertainties.
The most spectacular recent controversy in HED physics involved the behavior of cryogenic deuterium compressed by a strong shock wave. Deuterium is denser as a liquid than common hydrogen and allows experimenters to produce a higher pressure. With increasing compression, condensed hydrogen or deuterium changes from insulator to conductor. The transition, which is complicated by the breaking of molecular bonds, occurs in the warm-dense-matter regime (see figure 1). It is of interest to physicists not only for its relation to planets but also as a test of our fundamental understanding of a system with relatively simple constituents.
One of the basic ways to characterize the behavior of a material is to send a constant-speed shock wave through it and to measure the postshock state. It is fortunate that most people have little direct experience of shock waves—they are not friendly to structured objects, let alone to living ones. But through lightning, thunder, and sonic booms, we have some sense of familiarity with them, and most scientists are aware that a shock wave is a supersonic disturbance that heats and compresses matter. A shock wave generates both kinetic and internal energy; the postshock state reflects the amount of energy that is invested in breaking bonds, ionization, and other processes beyond straightforward heating.
Experimenters can often measure the velocities of the shock wave and the postshock material at the same time. In combination with the conservation of mass, momentum, and energy, those powerful measurements yield various thermodynamic quantities, including the ratios of final to initial pressure and density. For the data to be useful, though, measurements must be accurate to a few percent. Experimental results are often displayed as a plot of pressure versus density, such as shown in figure 2. The figure also shows theoretical model curves, the most long-standing of which is derived from the SESAME model, publicly available from Los Alamos National Laboratory. Simply put, the displacement of the data from the SESAME curve indicates an unexpected complexity in the behavior of deuterium. The pressures corresponding to that surprising behavior occur in those regions of giant gas planets where magnetic fields are generated.
Figure 2. Shocked, cryogenic liquid deuterium. This plot shows model curves and data from various experimental groups (indicated by different colors and symbols) for the behavior of shocked D2. The normalized compression is the ratio of the final density to the initial density of 171 kg/m3. All the data should be consistent to within the error bars, but they are not. The curves show the long-standing SESAME model (black), the behavior expected if the ratio of constant-pressure to constant-volume specific heats is 1.5 (gray), and a model by Marvin Ross (blue).
(Adapted from
The controversy primarily relates to the discrepancy between the data represented in the figure by red triangles and those indicated by gray diamonds. Before 1997, experiments that used gas guns to shoot plates of material at samples had produced data for pressures up to about 25 GPa. Those studies gave no reason to question the SESAME model, which was then the standard for comparison, even though the literature included several models with divergent predictions at higher pressure. 10 Then, in 1997, scientists at Lawrence Livermore National Laboratory (LLNL) used a novel technique for finding the velocities to obtain data in the same type of experiment, but at higher pressures. Their results, which led to the gray diamonds far to the right of the SESAME curve in figure 2, were widely acclaimed. A few years later scientists from Sandia National Laboratories used their advanced pulsed-power methods to launch plates of material at unprecedented velocities. Traditional diagnostic techniques yielded data, shown as red triangles, that contradicted the LLNL findings. The resulting controversy was not without sociological interest: Two large, proud national labs were put in opposition, and each sought to criticize the work of the other. Subsequent work involving LLNL and the Laboratory for Laser Energetics seemed to validate the Sandia results, but as yet no one has identified the error in the original LLNL experiment.
The story implies an important lesson, taught before but worth repeating. Science is hard. Competent people doing excellent work can get the wrong answer. A single set of measurements with a single technique should never be viewed as conclusive. Repetition of an important scientific result is of great value, especially if an independent method can be brought to bear. The dynamics of scientific funding and publishing are often at odds with that lesson. Those of us who serve as reviewers or in funding agencies should bear it in mind.
A window onto stellar processes
When stars explode or galaxies and other objects collide, they often produce radiative shock waves, which glow so intensely that they emit most of the thermal energy produced during shock compression. Scientists have devised several ways to produce and study radiative shock waves. The x-ray radiograph shown in figure 3 illustrates one example. The image depicts a shock tube filled with xenon gas, into which a slug of beryllium plasma was launched. The slug, irradiated by the Omega laser at the University of Rochester, attained a maximum speed of about 200 km/s.
Figure 3. Radiative shock in xenon gas. This x-ray radiograph captures a shock moving from left to right through xenon gas confined to a 575-µm-diameter tube; the length of tube shown is about 800 µm. The grid enables spatial calibration, and darker regions indicate higher xenon density. Not visible in the image is the beryllium plasma slug that drives the shock into the xenon. Radiation from the shocked xenon heats the walls of the tube, which expand and drive wall shocks radially inward; sharp kinks are visible where wall and primary shocks meet. The xenon near the walls experiences both the primary and the wall shocks and ends up in entrained flow near the walls to the left of the densest shocked xenon. The layer of dense xenon is not uniform, but rather appears to be subject to unstable fluctuations.
(Courtesy of Forrest Doss.)
The many complexities of high-energy-density systems
When the pressure on a material becomes greater than about 0.1 TPa, a number of new physical effects come into play, as shown in this plot. Consistent with figure 1, the boundary line that defines high energy density is in black and all lines are calculated for a simple model of aluminum, unless indicated otherwise.
The relativistic region corresponds to temperatures above 6 × 109 K. At those high temperatures, the kinetic energy of an electron exceeds its rest mass. At temperatures above 106 K or so and densities high enough so that a system can efficiently emit radiation, radiative energy fluxes and pressures become large enough to substantially alter material behavior. The corresponding region in the figure is labeled as a radiative plasma. The neighboring light pink region is partially bounded by a black horizontal line above which the radiation pressure would exceed 0.1 TPa if the radiation were confined in equilibrium with the radiating matter. In practice, establishing that equilibrium is a substantial challenge at the indicated densities. In the absence of trapped radiation, the light pink region would correspond to ideal plasma.
A plasma may be characterized, in part, by a parameter Γ, the ratio of electrostatic to thermal energies. That ratio increases as the density does. As Γ approaches 1, particles become correlated and traditional plasma theory fails; the resulting nonideal plasma corresponds to the light-blue region of the plot. The curve Γ = 1 (green for Al) is approximately coincident with the curve, shown in red, that specifies where the temperature equals the Fermi energy E F. In addition to the Γ = 1 curve for Al, the plot shows curves for hydrogen and an imaginary high-atomic-number material that never becomes fully ionized. If the density is sufficiently high, once the temperature drops below E F, the matter becomes both Fermi degenerate and strongly coupled. A correct description of the regime requires that electrons be explicitly treated as fermions and that the strong Coulomb interactions of the particles and the quantum mechanical structure of the ions be duly considered.
A nonradiative shock would produce an image with much less structure; indeed, understanding the structure seen in the figure has proven to be a challenge. In addition, several processes lead to effects that are not visible in the radiograph. Those include the heating of the xenon ions by the shock, the rapid transfer of energy from xenon ions to electrons, the radiation of that transferred energy by the electrons so as to heat the plasma ahead of the shock, and the cooling of the ions and electrons. The processes occur over a large range of spatial scales, so computer simulations of the system are a challenge. When described in terms of appropriate dimensionless parameters, the radiative shock shown in figure 3 is in the same regime as is a shock wave emerging from a supernova. Laboratory studies of radiative shocks, or of other dynamical systems that occur in astrophysics, provide important benchmarks for astrophysical computer simulations and have the potential to discover novel physical mechanisms also present in the astrophysical cases.
Empirical studies may also provide insights about the Sun. Experimenters can now produce conditions in the laboratory similar to those present at the boundary in the Sun where the heat transport changes from radiative to convective; moreover, they can measure x-ray transport under such conditions. Such measurements are of great interest to theorists, whose model predictions for the boundary location currently disagree with the location as determined by helioseismology—by more than 10 times the standard deviation of the measurement.
Energy and security
Inertial fusion has provided the motivation for the funding of most facilities where physicists study HED systems. The goal of inertial fusion is to implode a capsule that contains nuclear fuel and thus produce conditions in which nuclear fusion releases more energy than was used to initiate the implosion. As figure 4 shows, inertial fusion capsules access a broad slice through the parameter space of HED physics. The lowest density portions of those curves represent the laser-heated corona that has blown off the capsule surface. The corresponding reaction force drives shock waves into the capsule. The plasma that is blown off the surface is an ideal plasma. Following the curve to the right, which represents denser matter that has been shocked and perhaps further accelerated and compressed, rapidly leads to a regime in which particle correlations are important; at greater densities, strong coupling becomes significant. The cores of the fusion capsules are not the densest regions: The capsule curves turn upward at the cores and enter a regime of nonideal plasmas in which radiative effects matter.
Figure 4. Inertial confinement fusion as a high-energy-density system. The green curves show simulated properties of the nuclear fuel used in inertial fusion experiments. Time is fixed in the simulation; even so, properties of the fuel vary with location in a confining fusion capsule. The curve labeled “Omega” refers to the Omega laser facility at the University of Rochester; NIF is the National Ignition Facility at Lawrence Livermore National Laboratory. The plot also includes the curve (blue) for ionized beryllium with a ratio of electrostatic to thermal energies (ΓBe) equal to 1; at high energy densities, Be serves as a reasonable proxy for the complicated material used in actual fusion capsules.
(Courtesy of Riccardo Betti)
One might think that inertial fusion would have been supported in the US as part of the broad effort to produce energy for the future. Such support exists in Europe, where the HiPER (High Power Laser Energy Research) project seeks to go beyond the US National Ignition Facility in demonstrating the feasibility of inertial fusion for electricity production. In fact, the US has never systematically pursued the goal of electricity generation by inertial fusion. Instead, the US inertial fusion effort has been funded by what is now known as the National Nuclear Security Administration (NNSA)—the part of the Department of Energy (DOE) that supports nuclear weapons maintenance and research.
That emphasis has its sensible aspects. Consequences arise from the US’s decision to have nuclear weapons but not test them. The nation needs to develop a scientific understanding sufficient to maintain existing weapons without testing them, to assess the impact on civilian and military technology of nuclear weapons that others might use, and to sustain the scientific capability to cope with a world in which other nations continue to develop nuclear weapons. At the same time, it must train the individuals who will meet those needs. The above issues are addressed, in part, by inertialfusion and other HED studies.
But the organization of inertial fusion work in the US also has a nonsensical aspect. Rather than being funded in the context of potential sources of energy, or even of defense research, inertial fusion in the US is funded as part of the effort to clean up and replace the sites where nuclear weapons have been produced. The US would be wise to develop an inertial fusion energy program and also to find a way to place defense-relevant HED science, including inertial fusion, in a more sensible funding context. One way to do that would be to move the science part of the NNSA—a small fraction of its total budget—into the DOE office of Science. That office already has a small inertial fusion energy research budget and supports some university research in HED physics.
Science, industry, and medicine
High-energy-density physics lies at the core of numerous applications that promise both practical benefits and advances in fundamental knowledge. In big science, plasma-based particle accelerators offer a path forward for high-energy physics. Particle accelerators that rely on electromagnetic fields in vacuum have grown as large as is feasible. In plasma accelerators, the plasma is in a self-organized state; local application of intense energy creates a plasma wave whose intense wake is responsible for the acceleration (see the article by Chandrashekhar Joshi and Thomas Katsouleas in
Applications of HED physics in industry, medicine, and smaller-scale science projects will often involve tabletop systems—small pulsed-power systems or lasers like the HERCULES discussed in
When a system is brought to high enough pressure, quantum and relativistic effects become important and nonstandard correlations emerge. Thus HED systems are unlike any conventional state of matter and present a unique set of challenges to the experimentalists and theorists who work with them. Despite those difficulties, HED systems are well worth studying. Not only do they have much to teach us about the universe—what we are and where we come from—they also offer the promise of powerful applications that will affect many fields. On the large scale, HED physics can be applied to energy and security needs or in the service of high-energy particle beams. Applications on smaller scales include imaging systems that use x rays or particles to probe or modify structures ranging from jet turbines to brain tumors.
References
1. M. Schwarzschild, Structure and Evolution of the Stars, Dover, New York (1977).
2. R. Rhodes, The Making of the Atomic Bomb, Simon & Schuster, New York (1995).
3. Y. B. Zel’dovich, Y. P. Raizer, Physics of Shock Waves and High-Temperature Hydrodynamic Phenomena, Dover, New York (2002).
4. J. Nuckolls et al., Nature 239, 139 (1972). https://doi.org/10.1038/239139a0
5. P. Caldirola, H. Knoepfel, eds., Physics of High Energy Density: Proceedings of the International School of Physics “Enrico Fermi,” Course XLVIII, Academic Press, New York (1971).
6. G. Mourou D. Umstadter, Phys. Fluids B 4, 2315 (1992). https://doi.org/10.1063/1.860202
7. R. P. Drake, High-Energy-Density Physics: Fundamentals, Inertial Fusion, and Experimental Astrophysics, Springer, New York (2006).
8. National Research Council, Committee on High Energy Density Plasma Physics, Frontiers in High Energy Density Physics: The X-Games of Contemporary Science, National Academies Press, Washington, DC (2003).
9. D. Saumon T. Guillot, Astrophys. J. 609, 1170 (2004). https://doi.org/10.1086/421257
10. D. G. Hicks et al., Phys. Rev. B 79, 014112 (2009). https://doi.org/10.1103/PhysRevB.79.014112
More about the Authors
Paul Drake (rpdrake@umich.edu ) is the Henry Smith Carhart Collegiate Professor of Space Science at the University of Michigan in Ann Arbor, where he directs the center for radiative shock hydrodynamics.
R. Paul Drake. University of Michigan, Ann Arbor, US .
