Exotic physics with slow neutrons

I have to imagine that the great majority of scientists pay little attention to neutrons in their work. Lacking electric charge and bound to the nucleus by the strong interaction, neutrons are silent participants in most atomic- and larger-scale dynamical processes. Mainly, they serve to double the mass of atoms. Neutrons also don’t play much of a role in experiments in high-energy physics; there are no high-energy neutron accelerators, for obvious reasons. Although free neutrons are undoubtedly emerging from various violent events in the cosmos, their finite lifetime—about 15 minutes in their rest frame—severely limits the number of extraterrestrial sources that can transmit them to us directly.

Neutrons do occasionally take center stage; they figure prominently in nuclear processes such as fission and fusion and in the formation, evolution, and death of stars, including neutron stars and supernovae. In experiments, neutrons are most commonly used as weak, nondestructive scattering probes to measure static and dynamic correlations of density and magnetization in systems of interest for condensed-matter physics, chemistry, biology, materials science, geology, and other fields. In those cases, however, it is the dynamics of the sample, not of the neutron, that are of primary interest.

The reader may be surprised to learn that neutrons can be used to probe important questions in nuclear and particle physics, astrophysics and cosmology, and gravitation. To those ends, the same properties that ordinarily render neutrons “invisible” turn into experimental advantages. Their zero electric charge, tiny magnetic moment, and small electric polarizability make neutrons relatively insensitive to environmental fluctuations that would otherwise ruin delicate measurements.

So-called slow neutrons—those with energy of roughly 25 meV or less, for which the de Broglie wavelength is large enough to match the atomic spacings in condensed matter—can be manipulated by diffraction, mirror reflection, and other forms of coherent scattering. (That is also the energy regime in which neutrons are used as scattering probes.) And like neutral atom beams and trapped atoms, slow neutrons spend enough time in a reasonably sized apparatus to allow for precision experiments.

For many measurements slower is better, and one really wants a low-energy “decelerator” for neutrons. Although the laser-cooling technology that revolutionized atomic physics cannot be directly applied to neutrons, the particles can be cooled to millikelvin temperatures by exploiting interactions with quantized elementary excitations in condensed matter. Neutrons can, in a single step, convert almost all of their incident energy into phonons in superfluid helium or solid deuterium, or into magnons in solid oxygen, and come nearly to rest. At kinetic energies of 100 neV and below, the neutrons are cool enough to be totally reflected at all angles of incidence by solid surfaces or confined by magnetic or gravitational potentials; in that regime, they are commonly called ultracold neutrons, or UCNs. ^{1 , 2}

In this article I describe some of the experiments currently being done with slow neutrons at facilities worldwide. Several recent reviews present a broader survey of slow-neutron physics and related research areas, ^{3 , 4 , 5} and instructive books give overviews of neutron physics ⁶ and the beautiful subject of neutron interferometry. ⁷

Neutrons and nucleosynthesis

With a little contemplation, one can quickly realize that neutrons must be intimately linked to the early formation of elements after the Big Bang and to the relative abundances of those elements seen today. Imagine a thought experiment in which a hunk of ordinary matter is divided into separate piles of protons, neutrons, and electrons. The electrons, which are protected by charge conservation, and the protons, which are protected by the less widely advertised conservation law of baryon number, will be stable. But the pile of free neutrons will soon fall apart.

A neutron—a composite of two down quarks and an up quark—undergoes beta decay when the electroweak interaction changes one of the down quarks into an up quark and a W boson. That up quark remains bound to the others by the strong interaction, the three quarks together forming a proton. Meanwhile, the W boson quickly turns into an electron and an antineutrino, both of which typically escape. The decay process is n → p + e⁻ + ν̅_e + 0.782 MeV.

For neutrons bound inside a nucleus, however, the story is quite different: The scant 0.782 MeV released by neutron decay is typically smaller than the nuclear binding energy and comparable to the energy-level spacings. It’s therefore highly unlikely that the newly created proton would escape the nucleus or be excited to high energy levels—and it would run afoul of the Pauli principle were it to try to occupy an already-filled proton orbital. So although about half of our mass is made of unstable particles, we are rescued by the strong interactions that bind them inside nuclei and by the near equality of the neutron and proton masses, which leaves little excess energy for the decay products.

From Big Bang cosmology and the observed cosmic microwave background we know that the early universe was too hot to host atoms and nuclei and instead consisted of a plasma of neutrons, protons, electrons, neutrinos, photons, and probably other as-yet-unidentified constituents. (Our theoretical understanding of that history is well described in Steven Weinberg’s classic, The First Three Minutes, ⁸ and the basic calculations are now treated routinely in graduate texts on statistical mechanics. ⁹ ) There is no obvious protection for the free neutrons swimming in such a soup, and had the universe lasted in that state for too long, almost all of them would have decayed. Fortunately, many neutrons were saved from that fate: As the plasma expanded and cooled, nuclear reactions took over to bind the neutrons in nuclei, with most ending up in helium-4. Other present-day neutrons are the byproducts of stellar fusion reactions.

Naturally, the nuclear reaction rates in the primordial soup depend on the particle density, specifically the ratio η of baryons to photons. Now that η has been determined using data from the Wilkinson Microwave Anisotropy Probe (see Physics Today, May 2006, page 16 ), Big Bang nucleosynthesis has become a parameter-free theory except for the nuclear reaction rates. Better measurements of the neutron lifetime—whose uncertainty is the dominant source of error in predictions of the primordial ⁴He abundance—are needed to take advantage of the improved precision of astronomical measurements.

Unfortunately, recent measurements of the neutron lifetime are inconsistent. ¹⁰ One technique is to simultaneously measure the average number of neutrons N and their decay rate dN/dt in a well-defined fiducial volume of a slow-neutron beam. The rate dN/dt is inferred by counting protons, the products of beta decay, which can be trapped in a combination of electric and magnetic fields known as a Penning trap. The lifetime τ_n is equal to −N/(dN/dt). In the past couple of decades, beam experiments have produced estimates of τ_n ranging from 886 seconds to 889 seconds, with uncertainties near 0.3%. Figure 1 shows the electrostatic portion of a Penning trap that researchers at NIST will soon use in an attempt to measure the neutron lifetime to 0.1% accuracy.

A second approach to measuring τ_n is to confine neutrons in a material bottle. Neutrons will bounce from a flat surface if their kinetic energy is below the spatially averaged potential energy seen by the neutron—the so-called optical potential. For many neutron–nucleus interactions, that optical potential is of order 100 neV, larger than the kinetic energy of a UCN and large enough to make neutron optics practical. ¹¹ As a result, a UCN can be held in a material trap, or bottle, for long times. One can then simply measure N as a function of time, with N(t) = N(0)exp(−t/τ_n). Inconsistent recent experimental results, which differ in some cases by more than five standard deviations, show that the uncertainties from neutron interactions with the surface have been underestimated.

One can also trap neutrons with magnetic field gradients or, better still, with a combination of magnetic field gradients and gravity. That way, the neutrons never touch a material surface, and any loss of neutrons from the trap should only come from neutron decay. Those experiments are now under way.

Parity violation

In addition to the neutron lifetime, one can measure energy spectra and angular correlations of neutron decay products to shed light on symmetry violations in particle physics. Perhaps the best known measurement of that type is the famous 1957 experiment conducted by Columbia University’s Chien-Shiung Wu and collaborators at the US National Bureau of Standards (now NIST). ¹² At the suggestion of T. D. Lee and C. N. Yang, Wu and coworkers looked for, and found, parity violation in the weak interaction in the form of a lopsided angular distribution of electrons emitted during beta decay of polarized cobalt-60. The angular correlation—proportional to 〈s · p〉, where s is the spin of ⁶⁰Co and p is the electron momentum—is odd under a parity transformation: Momentum reversals are not accompanied by a corresponding reversal of spin.

Later experiments have sought to achieve the neutron equivalent of Wu and coworkers’ measurement—that is, the correlation 〈s_n · p_e〉 between the neutron spin and the electron momentum in neutron beta decay. That data, combined with the neutron lifetime, could help determine a key parameter of the standard model—the element V_ud of the so-called Cabibbo-Kobayashi-Maskawa matrix, which relates the quark-mass eigenstates and the weak-interaction eigenstates. Figure 2 shows the UCNA experiment, now in progress at Los Alamos National Laboratory, which uses polarized UCNs to measure the spin–momentum correlation. The sensitivity of neutron-decay experiments to possible physics and quark transformations beyond the standard model rivals that of similar searches now under way at the Large Hadron Collider.

The matter–antimatter imbalance

Inflation, the early exponential expansion of the universe following the Big Bang, is invoked in cosmology to explain the large-scale homogeneity, isotropy, and near flatness of the cosmos. To avoid apparent violations of causality—correlated temperature fluctuations in the microwave background, for example—the expansion must increase the radius of the universe by a factor of roughly e⁷⁰, which would enormously dilute any preexisting matter. In that view the matter and energy that later come to populate the universe are created after inflation through the decay of a scalar field from an initial state otherwise devoid of particles.

If that’s so, then where is the antimatter? After all, in the lab we always make equal amounts of matter and antimatter. Andrei Sakharov first raised the possibility that the matter–antimatter asymmetry of the universe should be calculable from basic principles. ¹³ He identified three criteria that, if satisfied simultaneously during the Big Bang, would cause an initially symmetric state to evolve into an asymmetric one: baryon-number (B) violation; charge–parity (CP) violation, which is equivalent to time-reversal (T) violation if CPT symmetry is preserved, as appears to be the case; and departure from thermal equilibrium. (See the article by Helen Quinn, Physics Today, February 2003, page 30 .) Although the standard model contains processes that satisfy the first two conditions and the Big Bang certainly could have satisfied the third, Sakharov’s theory underestimates the observed matter–antimatter asymmetry by many orders of magnitude when the known particles and particle interactions are used as the inputs. Therefore, adherents to the cosmological argument expect that B violation and new sources of T violation await discovery.

Both T violation and B violation should be detectable in sensitive neutron measurements. Time-reversal asymmetry has been sought, but not yet found, in neutron decay and would also be implied by a neutron electric dipole moment (EDM). ¹⁴ (See the article by Norval Fortson, Patrick Sandars, and Steve Barr, Physics Today, June 2003, page 33 .) Given that the neutron radius R is roughly 10⁻¹⁵ m and the electric charges of down quarks and up quarks are −e/3 and 2e/3, respectively, dimensional analysis suggests that the neutron’s EDM should be on the order of eR = 10⁻¹⁸ e-cm. But the minuscule size of the T-odd interactions suppresses the dipole moment, and the current experimental upper bound of the neutron EDM—set at the Institut Laue–Langevin (ILL) in Grenoble, France, using free neutrons in the apparatus shown in figure 3—is below 10⁻²⁵ e-cm. Already, that limit severely constrains supersymmetry theories and other models for physics beyond the standard model.

Experimentalists typically look for an EDM by searching for a shift in the precession frequency of a polarized particle upon a change in an external electric field. (The preferred interferometry technique is the same one used in atomic clocks; see the Physics Today special issue on Norman Ramsey’s method of successive oscillatory fields, January 2013 .) Various efforts are now in motion to improve the upper bound on the neutron EDM by about two orders of magnitude. That would severely wound minimal versions of supersymmetry and place constraints on specific theories within the Sakharov paradigm, in which the onset of the matter–antimatter asymmetry coincides with the electroweak phase transition—the point at which W and Z bosons, the transmitters of the weak interaction, are thought to have gained their mass. At that transition, our universe became, essentially, a superconductor for the quanta of the weak interaction.

Modern EDM experiments use ensembles of polarized UCNs and seek to maximize UCN number density, observation time, and the size of the applied electric field. The most ambitious such experiment, now under development by the US-based nEDM collaboration for the Spallation Neutron Source at Oak Ridge National Laboratory, will use superfluid ⁴He to slow UCNs by phonon emission and thereby increase their number density. And superfluid ⁴He can maintain large electric fields without suffering dielectric breakdown. Polarized ³He atoms will be added to the bath to polarize the neutrons and to serve as a comagnetometer that directly monitors the magnetic field fluctuations seen by the neutrons.

Evidence of B violation could come in the form of neutron–antineutron oscillations—the neutron analogue of neutrino flavor oscillations. Such oscillations would require a new interaction that changes B by two. Sensitive experiments on a slow-neutron beam at the ILL have yet to find evidence of the phenomenon, as have experiments at underground detectors used to look for neutrino oscillations and proton decay. No new measurements are under way, but a breakthrough in ongoing theoretical work would potentially breathe new life into the search.

The quark–quark weak interaction

In addition to the part of the weak interaction that initiates the neutron and nuclear beta decays discussed above, a lesser-known manifestation of the weak interaction operates only between quarks and does not produce objects that escape the nucleon. Given that quarks are permanently confined inside nucleons by the strong interaction, it should come as little surprise that the weak interaction between quarks remains mysterious—the strong interaction itself is poorly understood in that confining regime.

However, evidence of the weak interaction between quarks can be obtained by exploiting the fact that, to our knowledge, only the weak interaction violates parity symmetry. For example, an Oak Ridge collaboration known as NPDGamma—so named because it investigates reaction n + p → D + γ, the conversion of a neutron and proton into a deuteron and a photon—is now searching for evidence of weak interactions between quarks in protons and neutrons. As with the neutron beta decay experiments, the researchers are looking for the interaction in the form of a parity-odd correlation between spin and momentum, only in this case the spin of an incident polarized neutron and the momentum of the product γ are of interest. And whereas neutron beta decay produces an asymmetry of nearly 10%, the expected asymmetry in the NPDGamma experiment is just 10–40 parts per billion.

Because the quark–quark weak interaction is specified by the standard model, an accurate measurement of the parity asymmetry could be used to help infer the distribution and dynamics of quarks inside the nucleons. The interaction’s short range, about 1/100 the size of the nucleon, makes such measurements especially sensitive to the odds that two quarks in the nucleon are almost on top of each other and thereby correlated. (Double parton scattering, a new process recently observed at the Large Hadron Collider, is similarly sensitive to short-range quark–quark correlations.) The so-called lattice gauge theory formulation of strong interaction theory—a computation-friendly approach that has successfully reproduced the mass of the neutron, proton, and other bound-state properties of quarks—is now being applied to calculate the size of the parity-odd asymmetry from first principles.

The exquisite control over polarization achievable with slow-neutron beams and the small cross sections for neutron–matter interactions also make it possible to search for delicate forces on slow neutrons passing through macroscopic hunks of matter. A recent experiment at NIST looked for the rotation of the spins of transversely polarized slow neutrons moving through liquid helium and found an upper bound of 1 microradian per meter. That result sets the most stringent limit on the strength of any long-range parity-odd forces that might arise from the exchange of undiscovered, light, weakly interacting vector bosons.

Testing gravity

The first observation of a quantum mechanical phase shift on a neutron due to gravity was made using a neutron interferometer ⁷ like the one shown in figure 4. In the experiment, a neutron beam was coherently split and recombined by diffraction from three blades etched from a single, perfect silicon crystal. As the crystal was rotated about the incident-beam axis, the neutrons in the two interferometer arms saw different gravitational potentials, which generated a detectable shift in the relative phases of the two sub-beams.

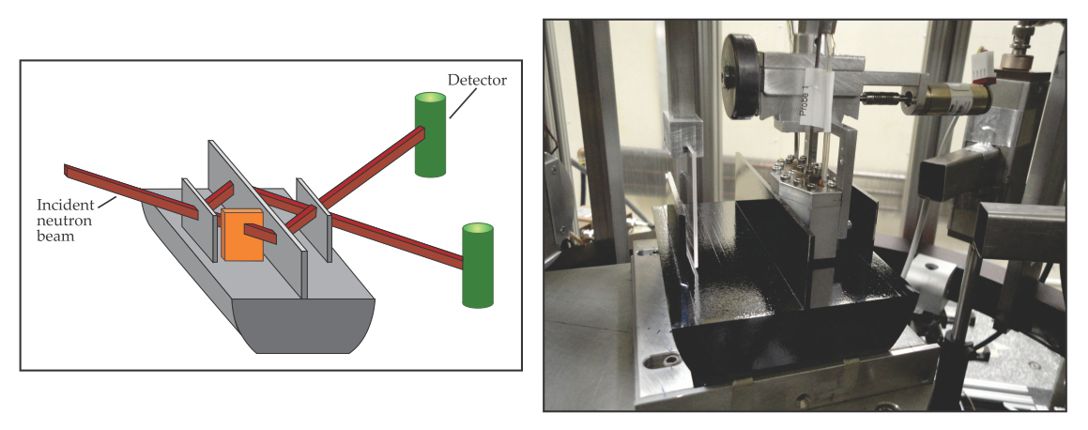
The experiment has become a textbook example of quantum mechanics. A similar phase shift can be caused by Earth’s rotation (the Sagnac effect) or by subjecting one of the neutron paths to an electric field (the Aharonov–Casher effect). Typically, the neutron beam is so dilute that rarely is more than one neutron in the device at a time. In fact, when one neutron is in the interferometer, the next often has yet to be liberated from its parent nucleus inside the reactor.

One can easily use magnetic fields to polarize the neutrons in the incident beam or manipulate the energy and momentum of the neutrons in an interferometer arm. That makes it possible to use neutron interferometers to test Bell’s inequalities, quantum decoherence, and other laws of quantum mechanics, and allows one to generate so-called Greenberger-Horne-Zeilinger states—quantum entanglements of three observable properties. And just as Lord Rayleigh used a light interferometer to measure the index of refraction of transparent materials, the neutron interferometer can be used to precisely measure a material’s neutron optical phase shift, which is proportional to the neutron–nucleus scattering amplitude. Precise measurements of the neutron–nucleus scattering length in light nuclei—⁴He and smaller—are of interest for few-body theorists seeking to understand the nuclear three-body force.

One potential explanation for why gravity is so much weaker than other interactions is that gravitational field lines escape into extra dimensions of spacetime at short length scales. (See the article by Nima Arkani-Hamed, Savas Dimopoulos, and Georgi Dvali in Physics Today, February 2002, page 35 .) Gauss’s law then implies that the inverse square law for gravity could be modified at length scales as large as 10 µm. ¹⁵ But our ignorance of the composition of dark matter and dark energy encourages other speculations about possible new interactions. Dimensional analysis of the dark energy density points toward 100 µm as the scale at which new phenomena might be found. The very small magnetic moment and electric polarizability of the neutron make it a good choice for testing gravity at those short length scales.

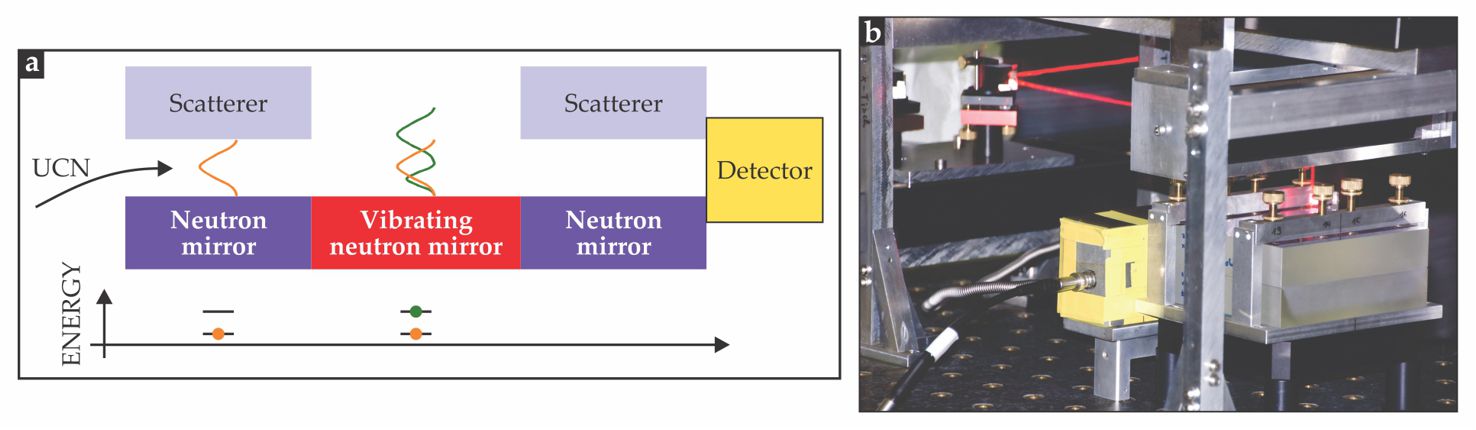
Sufficiently cool neutrons will float above a mirror in Earth’s gravitational field, with positions and energies prescribed by quantum mechanical bound states. In the lowest bound state, of energy 1.4 peV, the neutron hovers above the mirror at a distance of order 10 µm. Experiments at the ILL populated various bound states by forcing UCNs through a narrow gap above a neutron mirror. As the separation was varied, the intensity of the transmission of UCNs through the gap oscillated in accordance with theoretical predictions of the spatial extent of the bound states. (See Physics Today, March 2002, page 20 .) The measurement has become another textbook example of quantum mechanics ¹⁶ and has helped set an interesting bound on possible new weak forces at micron scales, since any nonstandard neutron–matter attractions on those length scales would modify the bound-state energies. Very recently, groups working at the ILL used the setup illustrated in figure 5 to observe transitions between low-lying gravitational bound states. Their experiments have created delicate superpositions of stationary quantum states that arise from the competition of strong and gravitational interactions. Indeed, slow-neutron physics may have more surprises left for us yet.