Do quantum spin liquids exist?
DOI: 10.1063/PT.3.3266
It was 1987, a year after high-temperature superconductivity was discovered in the cuprates. Over a lunch table in a small Chinese restaurant in downtown Tokyo, a group of physicists were excitedly discussing Philip Anderson’s new paper, 1 which proposed that the insulating phase of the cuprates is a quantum spin liquid (QSL). Similar conversations probably took place among physicists around the world.
One of us (Imai), then a young graduate student, wondered aloud what the big deal was. An unamused old-timer snapped, “You can surely try to read the new paper!” Still, he went on to explain that in 1973 Anderson had examined the possibility of a peculiar destruction of magnetism exhibited by spins arranged in a triangular lattice. 2 The new paper extended his original work to the square-lattice geometry found in the newly discovered cuprate superconductors.
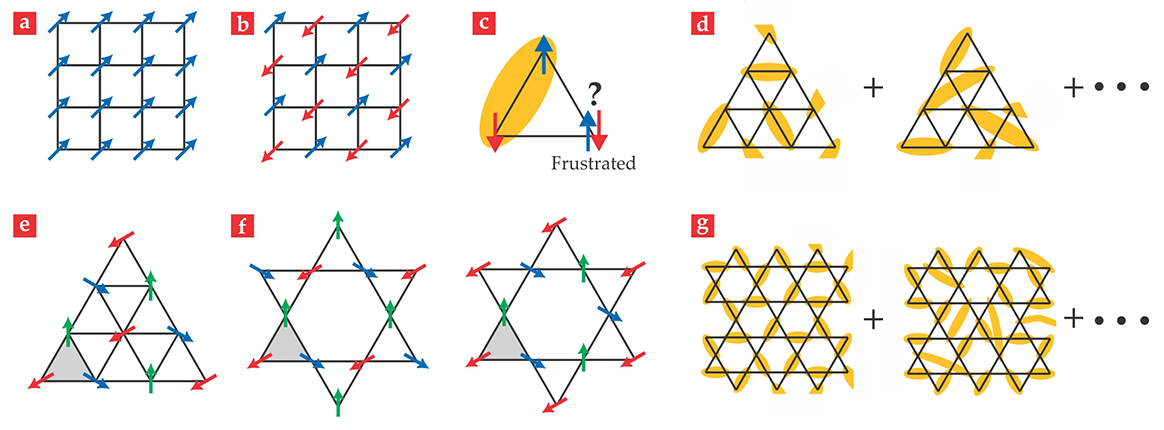
The QSL, in theory, represents a new state of matter. Unlike conventional magnetic states, such as the ferromagnetic state with parallel spins (figure

Figure 1. Frustration effects. (a) Ferromagnetic and (b) antiferromagnetic ordered states can exist on a square lattice without frustration. The arrows represent spins, and their colors identify their orientations. (c) Three
The discovery of cuprate superconductors had broader physics implications than just raising the superconducting transition temperature above the boiling point of liquid nitrogen. Lanthanum cuprate (La2CuO4) and related materials turn out to be ideal platforms for exploring the quantum effects of magnetism in low-dimensional systems.
The spin-½ Cu2+ ions in La2CuO4 are arranged neatly in a square lattice. Reducing the spin-projection quantum number
The trouble with antiferromagnetism
The fundamental ideas behind the QSL state trace back to a related debate from decades earlier over the concept of antiferromagnetism.
3
To examine the issues at hand, first recall what ferromagnets are. Above the Curie temperature
The underlying physics of ferromagnetism may be described by the Heisenberg Hamiltonian,
In contrast, the case of an antiferromagnetic Heisenberg model with a positive
Lev Landau therefore suggested that the Néel state
It took the invention of neutron diffraction during the post–World War II era to experimentally establish the existence of the Néel state. Since then, it has been found in a wide range of antiferromagnets on three-dimensional lattices. In the actual Néel state, the magnitude of the ordered magnetic moment is less than
The Néel state strikes back
In his classic 1973 paper,
2
Anderson proposed that in an edge-sharing triangular lattice, geometrical frustration could prevent spins from undergoing magnetic long-range order into a Néel state. The reasoning is that three spins at the corners of a triangle cannot be made mutually antiparallel (figure
In the RVB picture of chemical bonds in aromatic molecules such as benzene, the carbon–carbon bonds may be envisioned as a fluid of mobile single (C–C) and double (C=C) valence bonds that dynamically alternate their positions. In analogy, Anderson posited that neighboring
It turns out, however, that even edge-sharing triangular- lattice Heisenberg antiferromagnets can still form a Néel ordered state. In the so-called 120-degree structure (figure
In 1987 Anderson infused new life into the QSL idea by studying it in the context of antiferromagnetically interacting
Unusual suspects
Nonetheless, the search for new candidate materials that may harbor a QSL continued.
6
Over the past decade, two classes of materials have emerged as promising avenues to realize a QSL in two dimensions. One is the kagome Heisenberg antiferromagnet,
7
named after the Japanese word for a woven-basket pattern consisting of a corner-sharing triangular lattice (figures

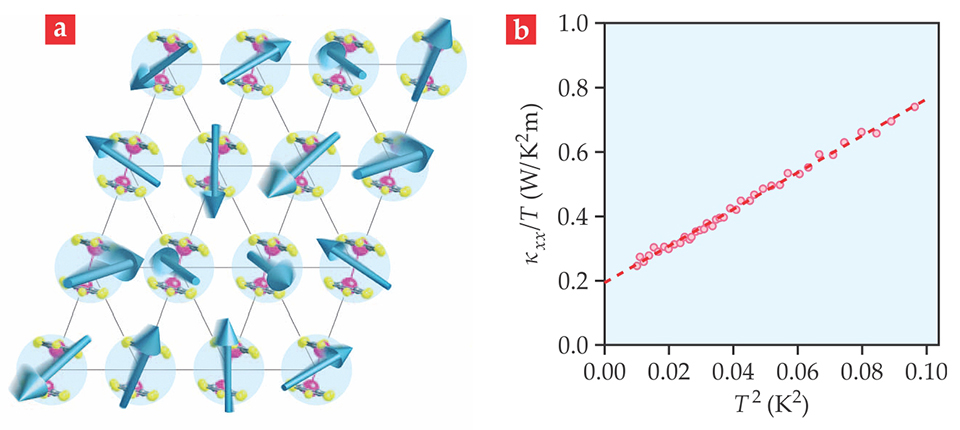
Figure 2. Organic quantum spin liquid candidates. (a) This depiction of the two- dimensional triangular planes in the organic compound EtMe3Sb[Pd(dmit)2]2 illustrates how pairs of Pd(dmit)2 molecules (highlighted in the blue circles) each share an unpaired, spin-½ electron denoted by the blue arrow. (b) As a function of the square of the temperature
Direct experimental proof of a QSL state is hard to come by. One of the unique features of a QSL is that the ground state does not follow the conventional Landau paradigm for phase transitions. Typically, interactions between particles in a collection will lead to ordering at low temperatures, and will thereby lower the overall symmetry. For example, the ferromagnetic transition breaks spin-rotational symmetry because the static moment of the electrons or ions must point in a specific direction. A local order parameter exists and becomes nonzero below a transition temperature. As a result, measurements of heat capacity, magnetization, and other thermodynamic quantities as a function of temperature show sharp anomalies in the vicinity of the transition temperature.
For a QSL, a local order parameter does not exist. The spins do not order and hence do not break spin-rotational symmetry, nor do they form singlets that are fixed to the crystal lattice and hence do not break translational symmetry. No phase boundary is crossed on cooling. So initial experimental tests for the QSL state in a material consist of looking for the absence of a phase transition. Measurements showing that the spins interact strongly yet fail to order, even at temperatures well below the interaction energy scale, would be consistent with a QSL state.
The question that immediately follows is whether the lack of ordering is a consequence of defects in the system. It is well known that quenched disorder in a spin system can lead to spin-glass physics, in which the dynamics slow down dramatically or freeze below a glass temperature without having long-range order. 9 Such spin freezing can be seen in magnetization measurements as a divergence between the temperature dependences of the spin susceptibilities of samples cooled in zero and nonzero magnetic fields. The absence of a glass transition at a temperature scale well below the interaction-energy scale would count as further evidence, albeit indirect, of the QSL state.
Terms of entanglement
The triangular-lattice molecular solids, mentioned earlier, pass all initial tests for being QSLs.
8
Specifically, they are κ-(BEDT-TTF)2Cu2(CN)3 and EtMe3Sb[Pd(dmit)2]2. Here, BEDT-TTF and dmit are particular organic molecules and Et and Me are ethyl and methyl groups. The structure of EtMe3Sb[Pd(dmit)2]2 is depicted in figure
One may ask whether there are more direct probes of the QSL. In fact, we have not yet discussed one of the defining properties of QSLs: They possess a high degree of quantum entanglement. Recall the picture of the QSL state as a superposition of all possible arrangements of singlets that cover the lattice, as shown in figures
The fractional quantum Hall state, in which the charge degrees of freedom have fractional statistics, is the one known experimental realization of such a highly entangled state. The QSL is a leading candidate to become the second known experimental realization.
The specific heat in the organic triangular-lattice compounds shows a large term that is linear in
Measuring thermal conductivity is another way to investigate spin excitations. In a magnetic insulator, the thermal conductivity contains contributions from phonons, magnetic excitations (spinons or magnons), and other propagating excitations. At low temperatures, the thermal conductivity of EtMe3Sb[Pd(dmit)2]2 has a large term linear in
The T-linear term is as large as the contribution by conduction electrons in metallic brass, so the mean free path for the heat-carrying quasiparticles must be exceedingly long—on the order of 1 μm. Such a large
The persuasive power of those measurements on the putative organic QSLs lies in the fact that they go beyond simply showing the absence of ordering and freezing. They show that the materials’ properties have specific temperature dependences that are consistent with spin excitations behaving as nearly free fermions rather than as magnons.
Another difficulty that arises in definitively proving the existence of a QSL in a particular material is that a vast array of theoretical QSL states are possible, each with slightly different properties. 6 Some QSLs have a so-called spin gap between the ground state and the first excited state. Others, such as the proposed state for the organics, are gapless.
Hence one of the best ways to make progress is to find a material with a theoretically tractable spin Hamiltonian and study the spin excitations directly with spin-sensitive probes. In the past several years, exciting developments have been made on both fronts for the Heisenberg model on the kagome lattice.
Advances in numerical calculations have shed much light on the possibility that the ground state of the
Herbertsmithite
Concomitant with the recent theoretical progress, experimental studies have identified one particularly promising

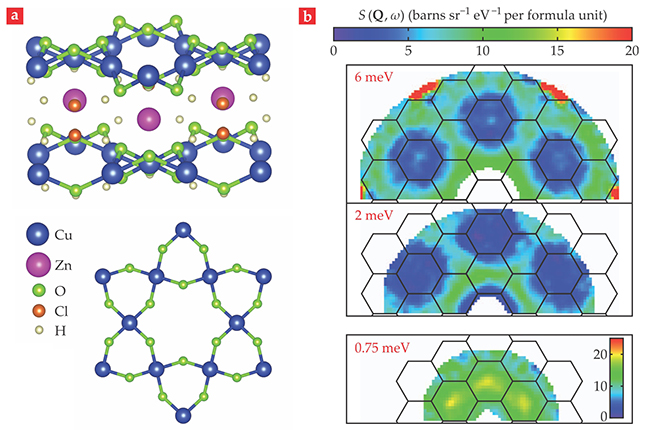
Figure 3. The kagome lattice as host for quantum spin liquid. (a) The crystal structure of the mineral herbertsmithite consists of copper and oxygen ions in kagome planes that are separated by nonmagnetic zinc, chlorine, and hydrogen interlayer ions. The bottom picture shows the two-dimensional structure of the kagome plane. (b) Inelastic neutron scattering measurements, made at 1.6 K on a single-crystal sample, map the spin excitations. The reciprocal-lattice unit-cell boundaries, drawn in black, provide orientation in reciprocal space. The signal at 0.75 meV is dominated by impurity scattering. However, plots of the dynamic structure factor
Importantly, single-crystal samples can be grown, and they have been used for various detailed measurements. We will highlight two recent experiments based on neutron scattering and NMR that shed valuable light on the nature of the possible QSL ground state.
As discussed in the
Plots of
The neutron data in figure
To further specify the ground state of the kagome Heisenberg antiferromagnet, one must probe the low-energy sector of spin excitations. In herbertsmithite, however, the nonmagnetic Zn2+ sites located between the kagome planes are occupied, with about 15% probability, by extra Cu2+ ions.
16
Those impurities also have spin
Because NMR is a local probe, it can separately detect nuclear spins that are far from defects or near defects. That ability makes it ideally suited for investigating the intrinsic low-energy spin excitations in the presence of defects. Recent NMR studies of herbertsmithite single crystals enriched in oxygen-17 or deuterium enabled measurements of intrinsic and defect-induced local spin susceptibilities (
In condensed-matter NMR measurements, one detects the resonant absorption of RF waves at the Zeeman frequency

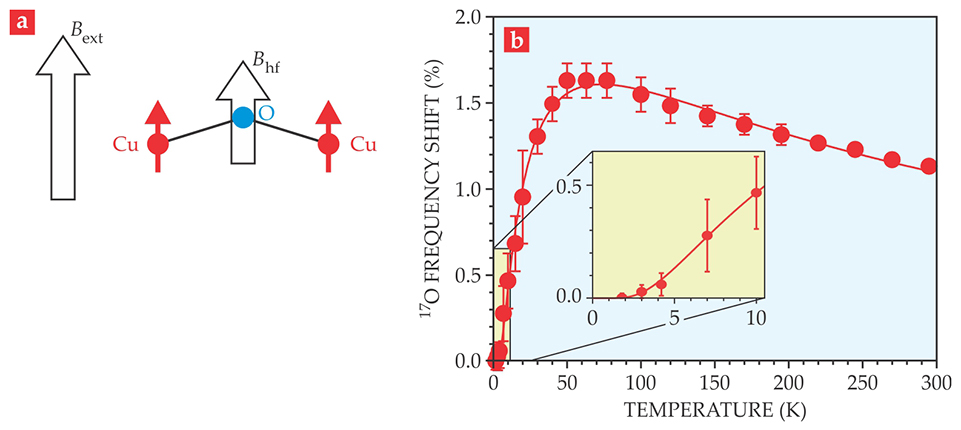
Figure 4. Intrinsic spin susceptibility of herbertsmithite. (a) An external magnetic field
In contrast,
The temperature dependence of the frequency shift,
17
shown in figure
Tip of the iceberg
The few example materials that we have discussed are hopefully just the first among many to be discovered that possess a QSL ground state. Beyond materials based on triangular and kagome lattices, other exciting new avenues for finding spin liquids involve highly frustrated pyrochlore lattices composed of corner-sharing tetrahedra with highly anisotropic interactions, and honeycomb lattices with bond-dependent interactions.
In the decade since Physics Today’s report on QSLs (February 2007, page 16

IMAGE BY SEAN K. TAKAHASHI

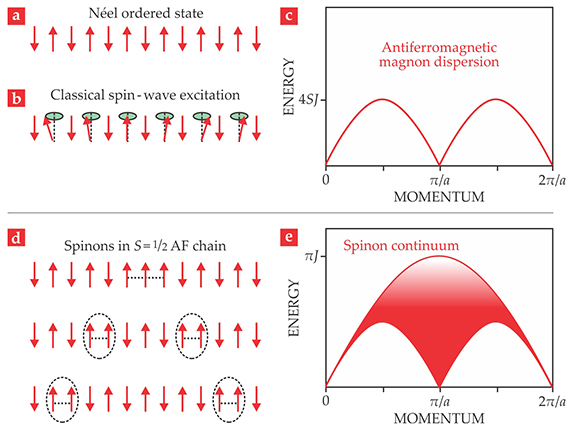
Box. Spin waves versus spinons
When the magnetic moments of a magnet enter an ordered state, the low-energy excited states are known as spin waves and the quantum of excitation is called a magnon. How the spin waves behave reveals the symmetry and strength of interactions and other fundamental properties of the magnetic system. In the high-temperature paramagnetic phase, the moments are equally likely to point in any direction. But in the low-temperature ordered phase, the moments must spontaneously select a unique direction along which to align the macroscopic magnetization. Goldstone’s theorem says that a consequence of that spontaneous breaking of a continuous symmetry is that the energy of the longest-wavelength spin waves will vanish.
Consider the simple example of antiferromagnetically interacting magnetic moments arranged on the one-dimensional lattice shown in
For quantum spins with
Because spin-rotational symmetry is not broken, the low-energy excitations cannot be classical spin waves. Rather, the
One may think of the

IMAGE BY SEAN K. TAKAHASHI
References
1. P. W. Anderson, Science 235, 1196 (1987). https://doi.org/10.1126/science.235.4793.1196
2. P. W. Anderson, Mater. Res. Bull. 8, 153 (1973). https://doi.org/10.1016/0025-5408(73)90167-0
3. P. A. Lee, Science 321, 1306 (2008). https://doi.org/10.1126/science.1163196
4. M. F. Collins, Magnetic Critical Scattering, Oxford U. Press (1989).
5. E. Manousakis, Rev. Mod. Phys. 63, 1 (1991); https://doi.org/10.1103/RevModPhys.63.1
M. A. Kastner et al., Rev. Mod. Phys. 70, 897 (1998); https://doi.org/10.1103/RevModPhys.70.897
R. J. Birgeneau et al., Phys. Rev. B 59, 13788 (1999). https://doi.org/10.1103/PhysRevB.59.137886. L. Balents, Nature 464, 199 (2010); https://doi.org/10.1038/nature08917
F. Mila, Eur. J. Phys. 21, 499 (2000). https://doi.org/10.1088/0143-0807/21/6/3027. M. P. Shores et al., J. Am. Chem. Soc. 127, 13462 (2005); https://doi.org/10.1021/ja053891p
Z. Hiroi et al., J. Phys. Soc. Jpn. 70, 3377 (2001). https://doi.org/10.1143/JPSJ.70.33778. K. Kanoda, R. Kato, Annu. Rev. Condens. Matter Phys. 2, 167 (2011); https://doi.org/10.1146/annurev-conmatphys-062910-140521
S. Yamashita et al., Nat. Phys. 4, 459 (2008); https://doi.org/10.1038/nphys942
S. Yamashita et al., Nat. Commun. 2, 275 (2011). https://doi.org/10.1038/ncomms12749. J. A. Mydosh, Spin Glasses: An Experimental Introduction, Taylor & Francis (1993).
10. M. Yamashita et al., Science 328, 1246 (2010). https://doi.org/10.1126/science.1188200
11. S. Yan, D. A. Huse, S. R. White, Science 332, 1173 (2011); https://doi.org/10.1126/science.1201080
S. Depenbrock, I. P. McCulloch, U. Schollwöck, Phys. Rev. Lett. 109, 067201 (2012); https://doi.org/10.1103/PhysRevLett.109.067201
H.-C. Jiang, Z. Wang, L. Balents, Nat. Phys. 8, 902 (2012). https://doi.org/10.1038/nphys246512. Y. Ran et al., Phys. Rev. Lett. 98, 117205 (2007). https://doi.org/10.1103/PhysRevLett.98.117205
13. J. S. Helton et al., Phys. Rev. Lett. 98, 107204 (2007); https://doi.org/10.1103/PhysRevLett.98.107204
P. Mendels et al., Phys. Rev. Lett. 98, 077204 (2007). https://doi.org/10.1103/PhysRevLett.98.07720414. T.-H. Han et al., Nature 492, 406 (2012). https://doi.org/10.1038/nature11659
15. D. Grohol et al., Nat. Mater. 4, 323 (2005). https://doi.org/10.1038/nmat1353
16. D. E. Freedman et al., J. Am. Chem. Soc. 132, 16185 (2010). https://doi.org/10.1021/ja1070398
17. M. Fu et al., Science 350, 655 (2015); https://doi.org/10.1126/science.aab2120
T. Imai et al., Phys. Rev. B 84, 020411 (2011). https://doi.org/10.1103/PhysRevB.84.020411
More about the Authors
Takashi Imai is a professor of physics at McMaster University in Hamilton, Ontario, and a senior fellow of the Canadian Institute for Advanced Research in Toronto. Young Lee is a professor of applied physics at Stanford University in Stanford and a member of the photon science faculty at SLAC in Menlo Park, both in California.






