Creating the perfect liquid in heavy-ion collisions
DOI: 10.1063/1.3431330
In 2005 the four experimental groups at Brookhaven National Laboratory’s Relativistic Heavy Ion Collider (RHIC) announced that collisions of gold nuclei at ultrarelativistic energies produced a “perfect liquid” of quarks and gluons. That’s something quite different from the gaseous quarkgluon state theorists and experimenters were expecting from quantum chromodynamics, the standard theory of the strong interaction.
Nucleons and all other hadrons are made up of quarks bound together by the strong interaction, which is mediated by gluon exchange. Unlike the chargeless photons that mediate the electromagnetic interactions, gluons carry color charge, the QCD analogue of electric charge. Therefore gluons, unlike photons, attract each other, which gives rise to the confinement of quarks inside hadrons.
A central consequence of QCD is the remarkable property of “asymptotic freedom,” the gradual vanishing of the strong forces between partons (quarks and gluons) with increasing proximity (see Physics Today, December 2004, page 21
Asymptotic freedom also seems to imply that ordinary hadrons can be “boiled” into a quark-gluon plasma (QGP) when the strong interactions are sufficiently weakened by high temperature or high density. That hardly sounds like a liquid. But in fact, the four RHIC groups concluded that the best parameter for describing what they found in the system created in those Au-Au collisions was one usually applied to liquids—namely, the ratio η/s of its shear viscosity to its entropy density. That ratio appeared to be nearly zero, making the system one of the first experimentally accessible perfect liquids ever isolated in the laboratory. 1
Quantum chromodynamics is an elegant and self-contained theory. But its predictions are notoriously difficult to extract. The development of lattice QCD in the 1980s put the study of quarks and gluons at high temperature on a firmer footing. That computational technique puts quark and gluon fields onto fixed lattice sites and links, and calculates their interactions by Monte Carlo methods. (See the article by Carleton DeTar and Steven Gottlieb in Physics Today, February 2004, page 45
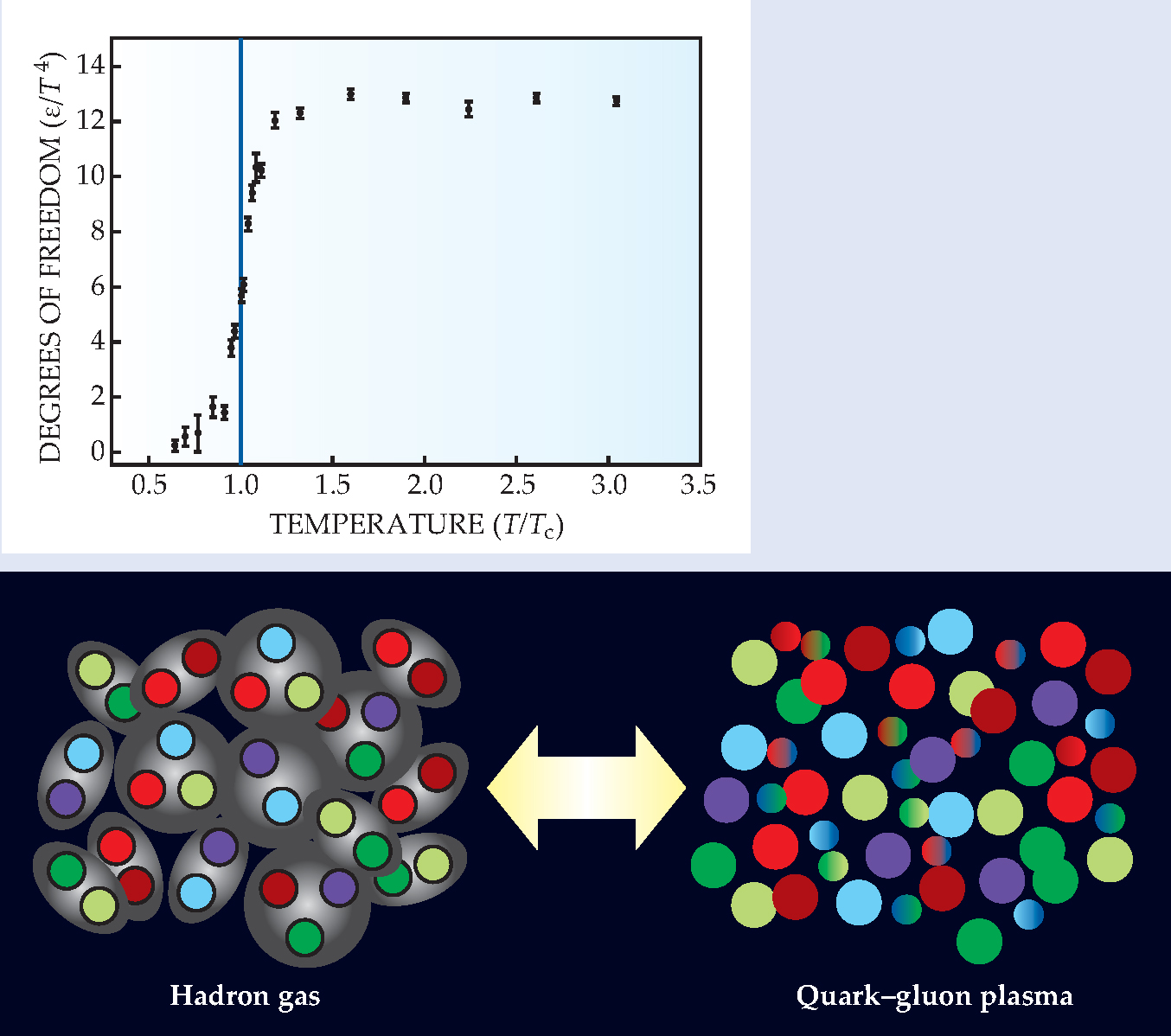
The Stefan-Boltzmann law tells us that the number of active degrees of freedom of a thermal system with energy density ε at temperature T is proportional to ε/T 4. Figure 1 shows that this ratio, as computed by lattice QCD, changes dramatically with temperature, jumping near a critical temperature T c of about 170 MeV (2 × 1012 K) to a high plateau. 2 That jump implies the existence of two phases: a low-temperature phase of hadrons and a high-temperature QGP phase characterized by quasi-free quarks and gluons.
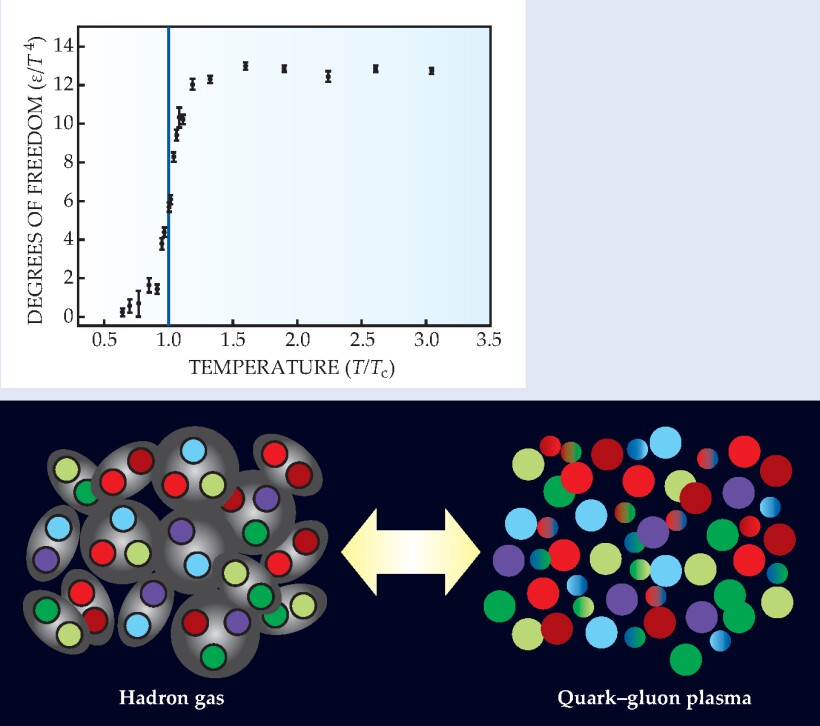
Figure 1. The number of thermally active degrees of freedom in a system at temperature T is proportional to its energy density ε divided by T 4. Plotted here is the expected temperature dependence of
(Adapted from ref. 2.)
Energy densities many times that found inside a normal nucleus are needed to produce a QGP. Such conditions haven’t been available since the first few microseconds of the early universe. Relativistic collisions of heavy nuclei provide the only terrestrial laboratory for studying matter at such extreme conditions.
Experiments at RHIC
RHIC was designed to test the QCD phase-transition predictions and to explore the properties of the QGP. Operating at Brookhaven since 2000, the collider produces the hottest, densest matter available in the laboratory so far (see figure 2). RHIC collides two countercirculating beams of ions with energies up to 100 GeV per nucleon. (A nucleon’s mass is about 1 GeV.) At the highest beam energies, the initial temperature generated by a head-on collision between two Au nuclei is inferred 3 to reach between 300 and 600 MeV.

Figure 2. The Relativistic Heavy Ion Collider at Brookhaven National Laboratory. (a) Aerial view of the collider and its complex of injection accelerators. (b) Inside the RHIC tunnel, two beam pipes for countercirculating heavy ions are surrounded by vacuum pipes and superconducting bending magnets. (c, d) Thousands of particle tracks emerging from typical heavy-ion collisions are displayed by the detectors of the PHENIX and STAR experiments at RHIC.

The ability to collide beams with nuclear mass ranging from protons to gold in nearly any combination lets experimenters at RHIC explore the nature and properties of the QGP. One can, for example, compare Au-Au collisions with protons or deuterons striking Au nuclei. Because the two RHIC beams can be brought into collision in several halls, an initial suite of four experimental detectors was constructed. Two large experiments, PHENIX and STAR, continue to operate today. The smaller experiments, BRAHMS and PHOBOS, have completed data taking.
To allow a broad survey of physics, each experiment, built and operated by an international collaboration of physicists, was optimized for a different set of experimental observables. Significant common capabilities allow the experiments to verify one another’s key results. Sample event displays from PHENIX and STAR are shown in figure 2.
The PHENIX detector consists of four spectrometers. Two of them measure particles emitted at scattering angles near 90° with respect to the beam direction. Consisting of multiple layers of tracking and particle-identification planes outside an axial field magnet, they provide precision measurement of photons, electrons, and hadrons. The distribution and correlations of those particles provide information about the collision region at times ranging from the collision’s initial pre-equilibrium stage, through the QGP phase, to the eventual “freeze-out,” when the system has cooled by rapid expansion and breaks apart. Closer to the beam directions are the two muon spectrometers, which are optimized to study the production and fate of mesons containing charmed and bottom quarks, rare and useful probes of the QGP.
The heart of the STAR detector is a time-projection chamber, which acts essentially as a 3D digital camera recording a large fraction of the thousands of charged particles produced in the collision. Sitting inside a large solenoid magnet, the chamber is surrounded by time-of-flight detectors and electromagnetic calorimeters to identify hadrons and select high-momentum electrons. STAR’s large angular coverage is ideal for studying collective plasma effects by measuring multi-particle correlations over a wide momentum range.
STAR and PHENIX have focused primarily on particles emitted close to the plane perpendicular to beam direction. Therefore, part of the role of BRAHMS and PHOBOS was to avoid missing interesting physics at angles closer to the beamline.
Experimental observables
Because different observables provide insight into different times in the history of a collision, the RHIC experiments measure many particle types over a wide range of momenta. Most of the collision products are hadrons with momentum spectra that are Boltzmann distributions boosted by a substantial radial expansion velocity. The relative yields of different hadron types are consistent with emission from a thermally and “chemically” equilibrated source 4 with a temperature near 170 MeV. Although that temperature is strikingly close to the predicted phase-transition temperature, it is not direct evidence of QGP formation. The distribution of particle types clearly indicates the presence of an equilibrated hot gas of hadrons at some stage in the evolution of the collision. Their momentum spectra seem to indicate that the final decoupling, or freeze-out, of the hadrons occurs when elastic scattering ceases at a temperature somewhere between 100 and 150 MeV.
Understanding of the system prior to freeze-out comes from two types of observables: measurements sensitive to the “flow” of the matter before freeze-out, and measurements of “hard” processes characterized by large momentum transfers. Hard processes include heavy-quark production and the formation of a pair of hadron jets. Jets are highly collimated sprays of hadrons resulting from the fragmentation of quarks or gluons scattered to high momentum. Produced early in the collisions, high-momentum quarks and gluons probe the hot, dense plasma as they traverse it.
Flow
The discovery that relativistic heavy-ion collisions produce a flowing medium is surprising if one expects that asymptotic freedom weakens interactions in a QGP. Nonetheless, the RHIC experiments observed “elliptic flow” in off-center collisions. Elliptic flow is manifested by a systematic modulation in the azimuthal angular distribution of collision products. The outgoing particles are emitted preferentially along the direction of the impact-parameter vector between the two colliding ions.
The modulation varies as
Although similar elliptic flow had been observed in lower-energy heavy-ion collisions at CERN and Brookhaven, those modulation amplitudes were much smaller. Hydro-dynamic simulations of the hot matter engendered in the RHIC collisions successfully reproduce the observed magnitude and increase of ellipticity with increasing impact parameter and emitted-particle momentum. Those results provide confidence in the validity of hydrodynamic descriptions of heavy-ion collisions.
Constraining the calculations with data let us infer more properties of the hot, dense system. The observed pattern and strength of the flow indicates a high degree of coordination among the constituents of the postcollision medium. Such coordination is more characteristic of a liquid than a gas. It may also help explain the extremely high opacity of the medium.
Hydrodynamics provides a tool for modeling the spacetime evolution of the system almost to the point where the emerging hadrons cease to interact with one another. But the moment of collision itself is not amenable to hydrodynamic treatment, because hydrodynamics requires the system to be in approximate local equilibrium. The earliest moments of the collision must involve nonequilibrium processes in which the incoming nuclei deposit energy, presumably by liberating quarks and gluons from their parent nucleons.
Although the thermalization time is still not known precisely, the hydrodynamic models that describe RHIC data best must begin evolution at 2 × 10-24 seconds. That’s much less time than is required for a particle to traverse a heavy nucleus.
Jet quenching
During the initial overlap of the Au nuclei, the quark and gluon constituents of the colliding protons and neutrons can scatter with large momentum transfer. Such scatterings create the “hard probes”—jets, heavy quarks, and high-energy photons—that must traverse the plasma on their way to the detectors.
Jet formation arises from quark confinement: When a quark is energetically struck, it radiates multiple gluons, and the resulting cluster fragments into a spray of emerging hadrons. Jets have been intensively studied in collisions of high-energy protons and antiprotons. The production cross sections and momentum distributions of jets and other hard probes can be reliably calculated from QCD by perturbative methods.
Before the start of RHIC, a key prediction was that a high-energy quark or gluon passing through very dense matter would suffer multiple interactions with plasma quarks and gluons, leading to large energy loss in the resulting jet—a phenomenon known as “jet quenching.” Only a few months after RHIC started up in 2000, first results on jet quenching from PHENIX and STAR showed suppression of energetic jet particles relative to the rate expected from collisions of free protons. As expected, the heavy-ion collisions appeared to be forming a dense, opaque medium. (See the article by Thomas Ludlam and Larry McLerran in Physics Today, October 2003, page 48
Figure 3 shows measurements of pions and photons emerging with very high momentum components transverse to the beam direction. The electron data in the figure signal the decays of heavy quarks. 5 The QGP is extraordinarily opaque to traversing gluons and light quarks, even at those high momentum. QCD attributes that opacity to plasma-induced radiation of gluons, akin to ordinary bremsstrahlung of photons by electrons. The low velocities of the heavy charmed and bottom quarks reduce the phase space available for gluon radiation, and thus should reduce their energy loss. Nonetheless, the electron measurements in figure 3 show that jets initiated by heavy quarks are suppressed just as much as the light-quark jets. That remarkable result indicates that the gluon-radiation energy loss predicted by perturbative QCD is insufficient to explain the observed jet quenching at RHIC.

Figure 3. Suppression of jets and heavy-quark hadrons in a quark-gluon plasma (QGP) (a) is shown by plotting suppression factors for pions and electrons emerging with high transverse momenta p t from head-on collisions between gold nuclei.
((a) Adapted from ref. 5.)
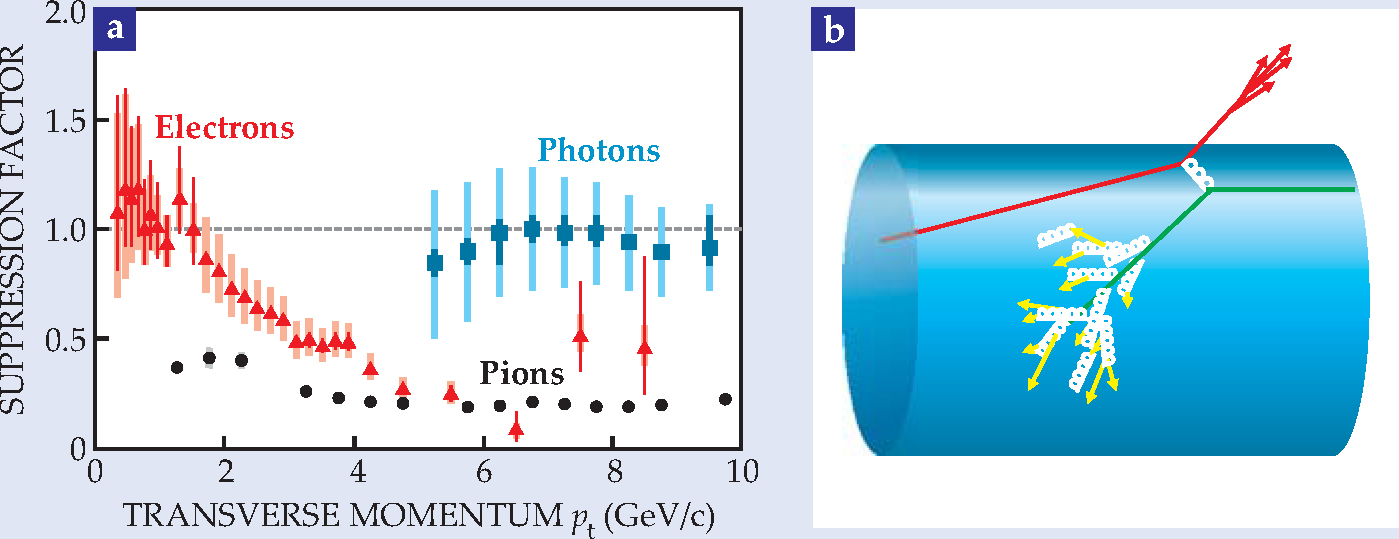
Because photons do not couple to the strong interaction, they provide the ideal control probe of the QGP. They should emerge from the plasma without significant energy loss. The high-energy photons are mostly produced in the initial, pre-equilibrium stage of the collision, with a spectrum that is well described by QCD. The figure 3 data show that the photons do indeed exit the plasma unscathed.
Lower-energy photons produced in the hot plasma provide information about the plasma temperature during its evolution. Hydrodynamic analysis of measured photon spectra yield the temperature estimates of 300 to 600 MeV for the early collision phase. That’s well beyond the transition temperature predicted by lattice QCD.
The strongly coupled plasma
By 2004, RHIC experiments had determined and reported several key properties of the hot, dense matter. 1 Its opacity to energetic quarks and gluons indicates extremely high density. Hydrodynamic descriptions reproduce the data and describe the collision from early times through expansion, cooling, and hadron formation, but only if η/s is taken to be very small. The system is therefore not the weakly coupled gas of almost freely moving quarks and gluons one would naively expect from asymptotic freedom. Instead, it is strongly coupled.
The strong coupling implies that some correlation among the quarks and gluons may survive within the plasma phase near T c and produce multiparticle interactions with near neighbors. Indeed, lattice QCD studies of energy-density correlations in a QGP at temperatures of 1-2 T c show small correlation peaks. The correlation is similar to the short-range order observed in ordinary liquids near the liquid-gas phase transition. 6
A strongly coupled classical system should be characterized by small η/s. The viscosity η is a measure of the inability of matter to transport momentum. In other words, viscosity indicates local deviations from perfect equilibrium that induce frictional forces and impede flow. A perfect classical liquid is inviscid—that is, η = 0. Models based on such a perfect liquid describe the flow of the medium created by collisions at RHIC remarkably well.
And yet a fully inviscid liquid clearly violates quantum mechanics. A system at a particular temperature cannot have degrees of freedom localized more precisely than the uncertainty principle allows. So it’s been difficult to model an in-viscid liquid in a relativistic quantum theory.
7
Remarkably, the string theory dualities that relate theories of strongly coupled particles to theories of weak gravitational coupling have yielded some progress toward quantum theories of inviscid liquids. (See the article on
The impact of that theoretical discovery was enormous. QCD is difficult to solve when the coupling is too strong for perturbative approximations. So there was a need for techniques that could address strong coupling. Physicists at RHIC were amazed to find that the duality of string theory with black holes offers a framework for calculating QGP dynamics. Since 2004, experimenters and theorists at RHIC have joined forces to devise measurements and theoretical techniques that work in tandem to extract the viscosity directly from the data.
Two teams have evaluated η/s via the diffusion of charmed quarks in the QGP. 9 Both found a strong correlation between the heavy quarks’ energy loss in the medium and the ellipticity of its flow. To reproduce the data, the calculations require the ratio η/s to be nonzero. But it must be very small, approaching the value expected by Kovtun.
It is clear that the collision systems produced at RHIC are nowhere near the weakly coupled regime of asymptotic freedom, which QCD attributes to the screening of color charge at short distances. That QCD analogue of electromagnetic Debye screening appears to be incomplete at typical interparticle distances in the heavy-ion collision plasmas. Consequently the QGP produced at RHIC is similar to other systems with strong coupling. But the presumption is that a weakly coupled plasma truly manifesting asymptotic freedom prevailed at an early phase of the Big Bang hotter than anything experimenters have reproduced.
Strongly coupled systems exhibit phase transitions, and many of them experience hydrodynamic flow. Examples include dusty plasmas such as in the rings of Saturn, which have been shown to have liquid and even crystalline phases. Similarly, warm, dense plasmas and strongly correlated condensed matter undergo transitions between phases with quite different physical properties. In all those cases there is a competition among different terms in the Hamiltonian.
In strongly coupled plasmas the potential energy wins out and the matter exhibits many-body interactions rather than being dominated by two-body scattering.
10
Phase transitions occur when the balance between the kinetic and potential energies changes, and minimum viscosity is observed at the transition point.
11
Dilute gases of ultracold fermions provide another example of a strongly coupled system (see the article on
Tuning the coupling is not possible in heavy-ion collisions, though the coupling strength may turn out to be different at the higher collision energies that will be accessible at CERN’s new Large Hadron Collider. But it is remarkable that both the coldest and the hottest matter on Earth exhibit very similar elliptic flow patterns, with η/s near the conjectured lower bound.
The discovery of the perfect liquid at RHIC is an important step toward understanding the nature of QCD matter. The next step is to quantify the properties of the hot, dense QGP. To that end, PHENIX and STAR are being upgraded to better exploit hard probes of the plasma—particularly heavy-quark states, which test color screening directly. RHIC’s collision rate is being increased by nearly an order of magnitude to allow a detailed tomography of the QGP with those rare probes.
Perfect liquidity was unanticipated at the beginning of the RHIC program. The newly discovered properties of the QGP will be of interest to a wide group of physicists. Cosmologists need better understanding of the correlations implied by strong coupling when the first hadrons were born in the immediate aftermath of the Big Bang. And the string-theory community is enthusiastic about the discovery of a physical system to which both string and gravity techniques have direct application.
We thank John Chin-Hao Chen, Peter Reynolds, and Edward Shuryak for help and valuable discussions.
References
1. Special issue, “First Three Years of Operation of RHIC,” Nucl. Phys. A 757 (2005).
2. F. Karsch, E. Laermann, A. Peikert, Nucl. Phys. B 605, 579 (2001). https://doi.org/10.1016/S0550-3213(01)00200-0
3. A. Adare et al. (PHENIX collaboration), Phys. Rev. Lett. 104, 13230 (2010).
4. J. Cleymans et al., J. Phys. G 32, S165 (2006). https://doi.org/10.1088/0954-3899/32/12/S21
5. A. Adare et al. (PHENIX collaboration), Phys. Rev. Lett. 101, 232301 (2008); https://doi.org/10.1103/PhysRevLett.101.232301
98, 172301 (2007); https://doi.org/10.1103/PhysRevLett.98.172301
S. S. Adler et al., Phys. Rev. Lett. 94, 232301 (2005). https://doi.org/10.1103/PhysRevLett.94.2323016. H. B. Meyer, Phys. Rev. D 79, 011502 (2009). https://doi.org/10.1103/PhysRevD.79.011502
7. P. Danielewicz M. Gyulassy, Phys. Rev. D 31, 53 (1985). https://doi.org/10.1103/PhysRevD.31.53
8. P. K. Kovtun, D. T. Son, A. O. Starinets, Phys. Rev. Lett. 94, 111601 (2005). https://doi.org/10.1103/PhysRevLett.94.111601
9. G. D. Moore D. Teaney, Phys. Rev. C 71, 064904 (2005); https://doi.org/10.1103/PhysRevC.71.064904
H. van Hees, V. Greco, R. Rapp, Phys. Rev. C 73, 034913 (2006). https://doi.org/10.1103/PhysRevC.73.03491310. B. Liu J. Goree, Phys. Rev. Lett. 94, 185002 (2005). https://doi.org/10.1103/PhysRevLett.94.185002
11. L. P. Csernai, J. I. Kapusta, L. O. McLerran, Phys. Rev. Lett. 97, 152303 (2006). https://doi.org/10.1103/PhysRevLett.97.152303
More about the authors
Barbara Jacak is a professor of physics at Stony Brook University in Stony Brook, New York. Peter Steinberg is a physicist at Brookhaven National Laboratory in Upton, New York.
Barbara Jacak, 1 Stony Brook University, Stony Brook, New York, US .
Peter Steinberg, 2 Brookhaven National Laboratory, Upton, New York, US .