Chemistry on the computer
DOI: 10.1063/1.2911179
When natural philosophers first tried to categorize the science of chemistry, they sometimes felt that as an experimental subject, it was strongly distinct from considerations of mathematics. In 1830 Auguste Comte wrote, “Every attempt to employ mathematical methods in the study of chemical questions must be considered profoundly irrational and contrary to the spirit of chemistry. If mathematical analysis should ever hold a prominent place in chemistry—an aberration which is happily almost impossible—it would occasion a rapid and widespread degeneration of that science.”
But with the dawn of quantum theory, the pioneers in that field began to realize that quantum mechanics had the potential to be a predictive theory of chemistry, just as Newton’s laws had already become for classical mechanics. As Paul Dirac said in 1929, “The underlying physical laws necessary for the mathematical theory of … the whole of chemistry are thus completely known, and the difficulty is only that the exact application of these laws leads to equations much too complicated to be soluble.”
Computational power has come a long way since 1929, but quantum chemists are still following Dirac’s instructions: “Approximate practical methods of applying quantum mechanics should be developed, which can lead to an explanation of the main features of complex atomic systems without too much computation.” Modern quantum chemistry, charged with the task of implementing that dream, thus has much in common with other computational physical sciences.
Today tens of thousands of research chemists routinely use the methods of quantum chemistry through computer software packages that contain more than a million lines of code. What do they use them for? How reliable are the results? What future challenges does quantum chemistry face? How do the parallel developments of quantum chemistry and condensed-matter theory compare? While no article of this length and nature can deeply answer all those questions, our goal is to give the reader a feel for the state of the art and its remaining limitations.
Some of the uses of quantum chemistry are described in
Wavefunction theory
Quantum mechanics enables, in principle, the study of chemistry without experiments. But in practice, the exact solution of the Schrödinger equation is intractable: Its computational cost grows exponentially with the number of electrons. One must make viable approximations, called theoretical model chemistries, a term coined by John Pople, who shared the 1998 Nobel Prize in Chemistry with Walter Kohn. Typical model chemistries include approximations of two types: restriction of the electronic wavefunction to the space of linear combinations of a finite number of basis functions, and simplification of the treatment of electron–electron interactions. A good model chemistry provides a useful tradeoff between the incompatible goals of accuracy and computational feasibility and is solvable to high enough precision to resolve small differences between large energies—attributes necessary for the study of chemical reactions.
The minimal basis set provides one basis function per occupied atomic orbital of each atom. For example, each carbon, nitrogen, or oxygen atom is assigned five basis functions: 1s, 2s, 2p x , 2p y , and 2p z . Such a small basis set is inadequate for most purposes because atomic orbitals are distorted in chemical bonds, and additional basis functions are added to accurately model the distortion. Functions of higher angular momentum than are occupied in the free atom are also added to describe polarization effects. A hierarchy of standardized basis sets has been developed and is built into modern quantum chemistry programs.
The simplest useful treatment of electron–electron interactions is the Hartree–Fock method, in which one treats the electrons in a mean-field sense, neglecting electron correlations but accounting for Fermi statistics. The wavefunction is an antisymmetrized product of the one-electron functions, or molecular orbitals, that are calculated to minimize the resulting energy.
Several different treatments of electron correlations offer useful tradeoffs between accuracy and feasibility. The simplest such treatment employs many-body perturbation theory, with the mean-field solution as the reference and the difference between the exact and mean-field Hamiltonians as the perturbation. The first nonzero correction, the second-order Møller–Plesset model, describes pair correlations (including van der Waals interactions) in a qualitatively correct way. The MP2 model systematically improves Hartree–Fock predictions of chemical observables such as structures and relative energies, though the accuracy of reaction energies is still deficient. With a medium-sized basis set, MP2 calculations are routinely performed on molecules of more than 100 atoms. Higher-order perturbation methods exist, but they are largely superseded by the infinite-order treatments discussed next.
Probably the most general and powerful wavefunction approach to the electron-correlation problem is the coupled-cluster method, which originated in nuclear physics and has been extensively developed in quantum chemistry. Coupled-cluster theory is based on the representation of the exact wavefunction as the exponential of a correlation operator acting on the mean-field solution. Approximate solutions are then derived from truncation of the power series of the exponential. The simplest useful truncation is after the second-degree term, which defines CCSD (CC for coupled cluster and SD for single and double substitutions). That model gives a self-consistent treatment of pair correlations and yields the exact solution for two-electron systems. It is applicable to molecules with up to 30–40 atoms.
A further correction, CCSD(T), includes a quasiperturbative estimate of the energy lowering due to three-body correlations. With a large enough basis set, CCSD(T) can yield chemical-reaction energies to an accuracy of better than 0.05 eV, which is sufficient for many predictive purposes (see
Given a theoretical model chemistry that defines the electronic ground state, almost any property of interest can be evaluated. Characterizing stationary points—local minima and saddle points on the potential energy surface—and the paths that interconnect them is the most important application area of quantum chemistry calculations. Calculations for many systems can be performed on a fast personal computer, but state-of-the-art applications typically require supercomputing resources. Bond lengths can be predicted to within 2–3% by Hartree–Fock theory and to better than 0.2% by CCSD(T). Relative energies and reaction barriers can be input into kinetic models to yield rates of chemical reactions. A wide range of other properties, such as permanent and induced electric dipole moments, frequency-dependent polarizabilities, and electronic excitation energies, can also be obtained.
Extracting physical insight from the electronic structure itself, however, is more difficult. The quantum mechanics of N correlated particles is based on a 3N-dimensional wavefunction, for which not much intuition has been developed. Simple 3D pictures are usually employed to relate the calculated wavefunction to known properties of atoms or functional groups, but they offer only limited insights. Localized orbitals, energy decompositions into physically motivated terms such as polarization and charge transfer, or properties of the electron density itself are typically used today.
Box 1. Quantum chemistry in industry: Saving the ozone layer
Chlorofluorocarbons are cheap, nontoxic, stable molecules that were once ubiquitously used as coolants, blowing agents, and industrial solvents—until it became clear in the 1980s that their very stability was contributing to atmospheric ozone depletion. That discovery led to the 1987 Montreal Protocol, which froze CFC production at 1986 levels, with the goal of a 50% reduction over the next decade. There was an urgent need to find suitable CFC replacements with greatly reduced ozone-depletion potential and minimal global warming potential.
Between 1988 and 1994, a team of DuPont scientists led by David Dixon (now at the University of Alabama) used quantum chemistry calculations on the highest-performance supercomputers to explore the behavior of CFC alternatives. What catalysts needed to be developed for producing the alternative substances? How much heat would be released or consumed in the production process? Would the new molecules have suitable refrigerant properties? What are their atmospheric lifetimes, and how much IR radiation would they absorb? What are their atmospheric degradation products?
Thermodynamic data were lacking for most of the possible CFC replacements. Methods based on quantum chemical wavefunction calculations were developed to calculate the missing data with accuracies similar to those of experimental measurements. The calculations even allowed researchers to identify errors in the experimentally measured heats of formation of two CFC species. With the thermodynamic properties of replacement molecules and associated radicals having been calculated, it became possible to understand their behavior in the environment, in production processes, and in use—for example, by predicting refrigeration cycles.
Quantum chemistry was used to predict the reaction rate of CFC alternatives with the hydroxyl radical, OH, which is the reactant responsible for the alternative molecules’ atmospheric lifetimes and thus their contributions to both ozone depletion and global warming. The IR absorptivity of each compound was accurately computed from first principles and used in computer models to predict the global warming potential. By using other kinetic parameters calculated from first principles, the DuPont team was able to predict to within 2% the activation energy of a pilot plant to synthesize the alternative compounds.
The ability to generate reliable thermodynamic and kinetic parameters has transformed computational quantum chemistry from simply a research tool to a true partner in the development of new chemicals and processes in the chemical industry. DuPont ceased commodity CFC manufacturing by the end of 1995.
Density-functional theory
As a function of 3N variables, the N-electron wavefunction becomes exponentially complicated as N grows large. In his 1998 Nobel lecture, Kohn spoke of an exponential “complexity wall” and even stated that for more than about 1000 electrons, the wavefunction “is not a legitimate scientific concept.” In contrast, the physical electron density is a function of just three variables. Of course, the costs of practical wavefunction methods scale much more reasonably with N, as a result of the approximations discussed previously. However, density-functional theory, which bypasses the wave-function to express the energy in terms of the density, has opened the field of first-principles simulations to systems far larger than can be studied with wavefunction techniques, as shown in
In 1964 Kohn and Pierre Hohenberg set forth their formal description of DFT and proposed the electron density n(r) as the fundamental variable. They proved the existence of an exact ground-state-energy functional, E[n(r)], and a variational principle for it. For fixed nuclear positions, the ground-state energy is the lowest possible energy that can be obtained from a search over all valid densities. And the density that yields the ground-state energy is the ground-state density.
However, the exact functional is unknown—and probably unknowable. The largest unknown term is the kinetic energy, for which an accurate approximate functional has proved elusive. The search for a kinetic-energy functional motivated Kohn and Lu Sham to map the original many-electron problem onto one of independent fermions under an effective potential, exactly described by a single-determinant wavefunction. The Kohn–Sham molecular orbitals that make up the wavefunction are used to evaluate the kinetic energy; they isolate the unknown part of the functional in a smaller term corresponding to the exchange and correlation energy. Kohn–Sham DFT is very efficient because it is a mean-field theory from a computational viewpoint, and nowadays it is the form of DFT that is almost universally employed.
Like wavefunction methods, DFT model chemistries are defined by the way they approximate the exchange–correlation energy. The first such approximation proposed, the local-density approximation, takes the effective exchange–correlation potential felt by an electron at any point in space to be a function of only the electron density at that point. That function was derived from the exact solution to the uniform electron gas, which is a reasonable model of a free-electron metal. Solid-state physicists adopted DFT and the LDA in the late 1970s with extraordinary success, and thus began the extremely fruitful line of first-principles calculations in solids. From very simple solids, the focus quickly turned to surfaces, defects, and interfaces. The calculations were accurate to within 1% for geometries and within a few percent for cohesive energies, elastic constants, and vibrational frequencies. However, the LDA overestimates binding energies of molecules by around 20%—almost as much as mean-field theory underestimates them—so it did not find wide use in quantum chemistry.
In the late 1980s, DFT became widely accepted in the quantum chemistry community, mainly because of the work of Axel Becke. Becke took the next proposed approximation to exchange and correlation, the generalized gradient approximation, and improved it to satisfy the demands of chemistry. GGAs allow the correlation energy to depend on the local gradient of the density in addition to its local value. They thereby offer a more flexible description of systems that differ greatly from the idealization of the uniform electron gas. Modern GGAs estimate the atomization energies of small molecules with five times better precision than the LDA, so they have become a standard way of computing ground-state properties of extremely varied systems.
The strategy of introducing higher-order local derivatives of the electron density has branched out in different directions explored by both physicists and chemists. Physicists led by John Perdew are considering a hierarchical set of approximations—his so-called Jacob’s ladder—based on satisfying as many fundamental principles as can be summoned, thus preserving DFT as a first-principles theory. Chemists, on the other hand, often perceive DFT as a semiempirical approach. They have constructed functionals in which a few empirical parameters are chosen to best reproduce the experimentally measured chemical properties of representative systems. Functionals of both kinds are used by both communities.
There are still clear limitations in the accuracy of GGAs for problems such as energy barriers and even reaction energies themselves. Becke proposed modifying the functionals by mixing in a fraction of the wavefunction exchange energy associated with the Kohn–Sham orbitals. The procedure and the amount of mixing initially proposed—the half-and-half functional—were justified on simple and elegant theoretical grounds. Becke later generalized the admixture to include some empirical parameters. That work marked the birth of hybrid functionals, which are a departure from Kohn–Sham theory. Hybrid functionals yield useful accuracy improvements over pure functionals for nonmetallic systems, so they are the functionals of choice in most molecular DFT calculations done by chemists. But they have not been widely adopted by physicists, partly because the higher efficiency of their algorithms for condensed-matter systems is dramatically degraded by hybrid functionals.
As proposed by Kohn and collaborators, DFT is strictly for the electronic ground state. Eberhard Gross and others extended it to electron dynamics in a way conceptually parallel to going from the stationary Schrödinger equation to its time-dependent form. Time-dependent DFT thus enables the study of electron dynamics and, even more importantly, excited states of many-electron systems. Many of today’s time-dependent DFT calculations make direct use of functionals from the ground-state theory, which have no frequency or time dependence. That approach involves comparatively little effort and yet is often quite accurate for molecular excited states. It is also natural for the study of genuinely time-dependent problems, such as the nonadiabatic electron dynamics associated with time-dependent perturbations—for example, ions shooting through solids. Although time-dependent DFT originated in condensed-matter physics, it is now used and developed by physicists and chemists alike.
Modern DFT calculations are predominant in both quantum chemistry and condensed-matter physics because present-day functionals usually offer the best tradeoff between accuracy and feasibility. They are routinely performed on systems of hundreds of atoms. Potential-energy surfaces can be explored using derivative methods, and a system’s response to small perturbations can be computed. Often the accuracy is sufficient for interpretive and sometimes even for predictive purposes. The failures and limitations remaining in DFT are associated with deficiencies in the exchange and correlation functionals. In the exchange functional, for instance, the electron can interact unphysically with a fraction of itself, which can cause excessive delocalization: An extreme example is the incorrect dissociation of He2 + to two He0.5+ ions. In the correlation functional, researchers face the lack of nonlocal dispersion interactions and the problem of treating highly correlated systems. The limitations of DFT are major enough to inspire intense efforts to overcome them in both the chemistry and physics communities.
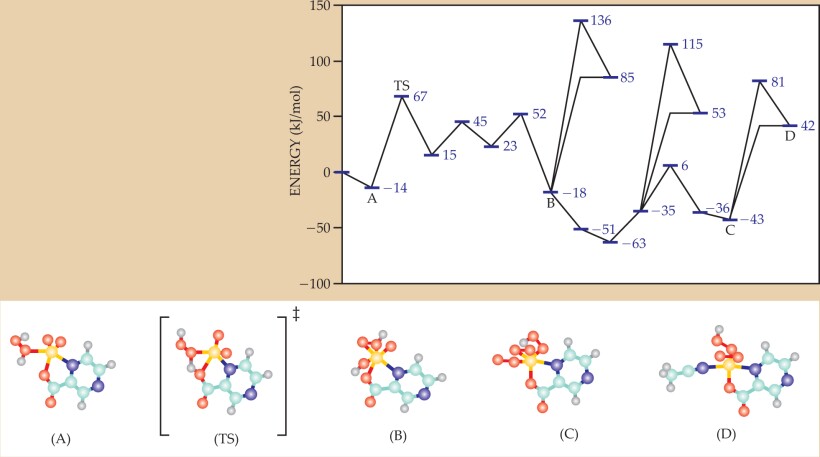
Box 2. Unraveling catalytic cycles
A chemical reaction mechanism connects reactants and products (local minima on the potential energy surface) via transition structures (saddle points). A simple reaction has a single transition structure, but most reactions are more complicated, particularly catalyzed reactions, which follow a path with multiple energy barriers. The figure depicts the configurations of a vanadium-based catalyst that enables the oxidation of alkanes by hydrogen peroxide in acetonitrile. Each purple bar represents an optimized structure from a density-functional-theory calculation. Five of the structures are shown below: TS is a transition state, and the others are local minima. The yellow atoms are vanadium, the red are oxygen, the blue are carbon, the purple are nitrogen, and the gray are hydrogen.
The catalyst creates reactive hydroperoxy radicals by decomposing hydrogen peroxide. The catalyzed decomposition is controlled by two steps with roughly equal energy costs, with an overall activation energy calculated to be 75% lower than that of direct decomposition, in agreement with experiments. Kinetic modeling based on the computed mechanism has been used to predict the dependence of the oxidation rate on conditions such as catalyst and reactant concentrations. Those results are within a factor of 10 of experiment—still satisfactory, since reaction rates vary over many orders of magnitude. Calculations are especially valuable for so rich a mechanism, but increasing complexity presents new challenges to the use of quantum chemistry methods. (Figure courtesy of Rustam Khaliullin.)
Box 3. First-principles molecular dynamics
After analytic energy derivatives were successfully incorporated into density-functional theory, the calculation of adiabatic forces acting on nuclei became routine. First-principles molecular dynamics calculations, which follow the Newtonian dynamics of classically treated nuclei under the DFT forces obtained at every time step, have made electronic-structure calculations applicable to the study of liquids, from biochemical systems to the liquid iron in Earth’s core. It is a field of enormous potential and great challenges, which researchers are starting to explore with other model chemistries as well. The figure captures the deformation of the electron density, as contours in a plane, in a snapshot of liquid water. (Figure courtesy of Marivi Fernandez-Serra.)

Present and future challenges
Practical DFT and wavefunction calculations constitute a well-developed core to quantum chemistry that synergizes strongly with parallel developments in condensed-matter physics. They are used across all areas of modern chemical research: About 10% of all chemical research publications now involve quantum chemistry calculations. In that sense, quantum chemistry is joining experimental techniques such as mass and x-ray spectrometry as a standard tool for research in chemistry.
However, in some ways, that maturity is only skin-deep. Unlike those used in other computational physical sciences such as weather forecasting or classical molecular dynamics, the underlying numerical methods used in quantum chemistry are not yet fully mature and stable, because the standard theoretical model chemistries have significant failings. The following are a few of the most interesting and pressing research frontiers that quantum chemistry is facing. But just as in most other areas of science, it is likely that many of the future breakthroughs will come from unanticipated directions.
Locality and nonlocality of electron correlation. The central issue that makes electronic structure a rich and nontrivial subject is its many-body nature. It is helpful to separate correlation effects into those associated with nearly degenerate electron configurations (see “Strongly correlated systems,” which follows) and the remaining so-called dynamic correlations.
Dynamic correlations are mostly spatially localized. While locality is explicit in the correlation functionals of DFT, it is not directly evident in wavefunction methods. A challenge and an opportunity is to exploit localization to break the unphysical increase in computational cost with system size. In addition to truncating by excitation level, the goal is to truncate according to some distance-based criterion. Proof of concept was first demonstrated by Peter Pulay in the early 1980s; nowadays local models can reduce the cost of many-body methods to a linear function of the system size. However, constructing a local model that retains a good model chemistry is still an open challenge.
A related problem is the difficulty of approaching completeness of the atomic-orbital basis sets used for correlated electrons. From theory, one expects and observes slow L −3 convergence of the correlation energy with respect to the highest angular momentum L of the basis functions. Describing two-particle and higher correlations in terms of the products of one-particle basis functions is both inefficient and nonlocal. One way forward is to augment the basis with two-particle functions that correctly describe the wavefunction in the vicinity of electron–electron coalescence. That research is yielding significant improvements in convergence, although many technical and practical issues remain open.
Although localizability of electron correlation yields many useful results, there is still a need for nonlocality. Correlations have a nonlocal component associated with dispersion interactions between systems, overlapping or not. Such interactions are crucial for correctly modeling large-scale self-assembly in nanoscale and mesoscale systems and for biochemical systems. Nonlocal correlation effects are neglected in standard DFT functionals, so research is under way to modify the functionals, whether by simple empirical corrections or by first-principles constructions, to include more nonlocal character. In that sense, the future modeling needs of the two branches of quantum chemistry are diametrically opposed.
Strongly correlated systems. A system that exhibits genuinely strong electron correlations cannot be well described by a single electronic configuration. Rather, the interaction among multiple configurations produces interesting effects such as molecular analogues of the Kondo effect and magnetic couplings of transition metal atoms with partly filled d shells. Proper modeling of such systems lies at the very limit of—or even beyond—the standard methods because both Kohn–Sham DFT and wavefunction methods begin with a single configuration and correct imperfectly for correlation effects.
At present, the usual approach to strongly correlated systems is to solve the Schrödinger equation exactly in a small strongly correlated space of so-called active orbitals, with the rest of the system treated in a mean-field approximation. Because of the exponential cost of the exact treatment, there is a hard upper limit of approximately 16 active orbitals—insufficient to treat more than one or two atoms with active s, p, and d shells. (The separation of a correlated space resembles what is done in dynamical mean-field theory and related techniques in condensed matter, as described in the article by Gabriel Kotliar and Dieter Vollhardt, Physics Today,
One possible new approach to highly correlated systems is the physicists’ density-matrix renormalization group, which builds up descriptions of the many-body Hamiltonian atom by atom (or region by region) in an iterative way, while keeping the lowest-energy state at every iteration. At present, it is a method best suited to systems with 1D connectivity.
Another alternative may be to use reduced density matrices. The ground-state energy of any system can be exactly expressed in terms of the two-particle density matrix instead of the N-electron wavefunction, but the equations that determine that matrix couple to higher-order density matrices, and truncations of that hierarchy are under development. The direct search for such matrices by suitably constrained energy minimizations confronts the unsolved N-representability problem: Is there actually an N-particle wavefunction that corresponds to the energy-minimizing density matrix?
The nano- and mesoscales. Chemistry is moving in many directions, and researchers in neighboring fields in the bio-, geo-, nano-, environmental, and materials sciences are asking for predictive computational methods that can deal with larger and more complex systems. The recent progress in accuracy and scalability of quantum chemistry methods has substantially extended their applicability into those fields. In many fields, quantum chemistry methods are meeting, and even marrying, the methods of condensed-matter theory—an example of physics and chemistry meeting at the nanoscale. There the frontier of decreasing sizes that can be probed by experiments meets that of increasing sizes amenable to simulations, and new synergies between the two are foreseeable. There is also a demand for calculations on mesoscale and larger systems, where multiscale approaches represent an exciting frontier in which quantum chemistry methods treat just the finest length scale.
Progress in electronic-structure methods is allowing researchers to get around Kohn’s complexity wall. On the other side of it, however, there is another wall: the complexity of the nuclear degrees of freedom. The prediction of molecular structure is an exponentially complex problem too. Molecular-dynamics calculations are needed in many of the fields into which quantum chemistry is extending, such as those that address liquid systems (see
Quantum chemistry and the future of computing. Computational quantum chemistry depends critically on computer resources. The exponential increase in computer power over the past four decades, as described by Moore’s law, has combined with developments in theory to make large-scale practical applications a reality today. On the one hand, the fact that only an inexpensive high-performance personal computer is required has made the barrier to adopting computational chemistry calculations extraordinarily low. On the other hand, supercomputing resources have enabled the crossing of new frontiers in applications. Future developments in computing will offer both challenges and opportunities. Challenges include the difficulty of mapping the algorithms of quantum chemistry onto new computer architectures that are increasingly parallel: The supercomputers of the next decade will have between 10 000 and 100 000 processors. But opportunities may also come from revolutionary changes in computing paradigms—for example, nothing could simulate a quantum system like a quantum computer!
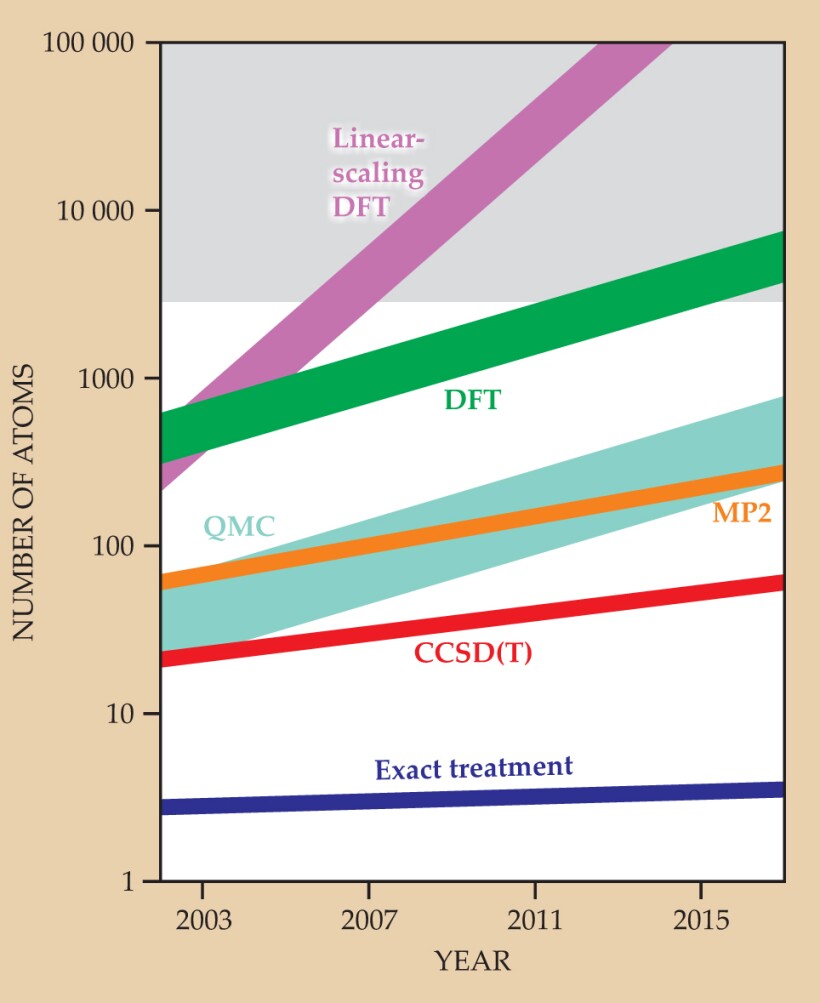
Box 4. Scaling of computational needs with system size
Given a finite basis set, the memory and processor needs for an exact treatment of electron interactions (the so-called full configuration interaction or full CI) grow exponentially with the number N of atoms in the system. Model chemistries introduce approximations that reduce the scaling: N 3 for density-functional theory (DFT), Hartree–Fock, and quantum Monte Carlo (QMC, a basis-independent, stochastic wavefunction approach); N 5 for second-order Møller–Plesset perturbation theory (MP2); and N 7 for the coupled-cluster method CCSD(T). The figure illustrates an estimated evolution of the size of the systems solvable by each method if computer power continues to double every two years or so. In the early 1990s, Weitao Yang, Giulia Galli, and Michele Parrinello realized that a reduction to linear-scaling complexity could be achieved for DFT if the solution to the electronic problem could be re-expressed in a localized language. After a decade of developments by chemists and physicists, several linear-scaling electronic-structure methods are now in use that can address systems with as many as a few thousand atoms. Other theories, such as linear-scaling QMC, have also achieved improved scaling through locality. Reduced-scaling wavefunction theories are in development. The shaded area at the top shows the nuclear complexity wall described in the text.
References
1. F. Jensen, Introduction to Computational Chemistry, 2nd ed., Wiley, Hoboken, NJ (2006).
2. R. J. Bartlett, M. Musiał, Rev. Mod. Phys. 79, 291 (2007). https://doi.org/10.1103/RevModPhys.79.291
3. C. Fiolhais, F. Nogueira, M. Marques, eds., A Primer in Density Functional Theory, Springer, New York (2003). https://doi.org/10.1007/3-540-37072-2
More about the authors
Martin Head-Gordon is a professor of chemistry at the University of California, Berkeley, and a faculty chemist at Lawrence Berkeley National Laboratory. Emilio Artacho is a professor of theoretical mineral physics at the University of Cambridge, UK.
Martin Head-Gordon, 1 University of California, Berkeley, US .
Emilio Artacho, 2 University of Cambridge, UK.




