Bulk Metallic Glasses

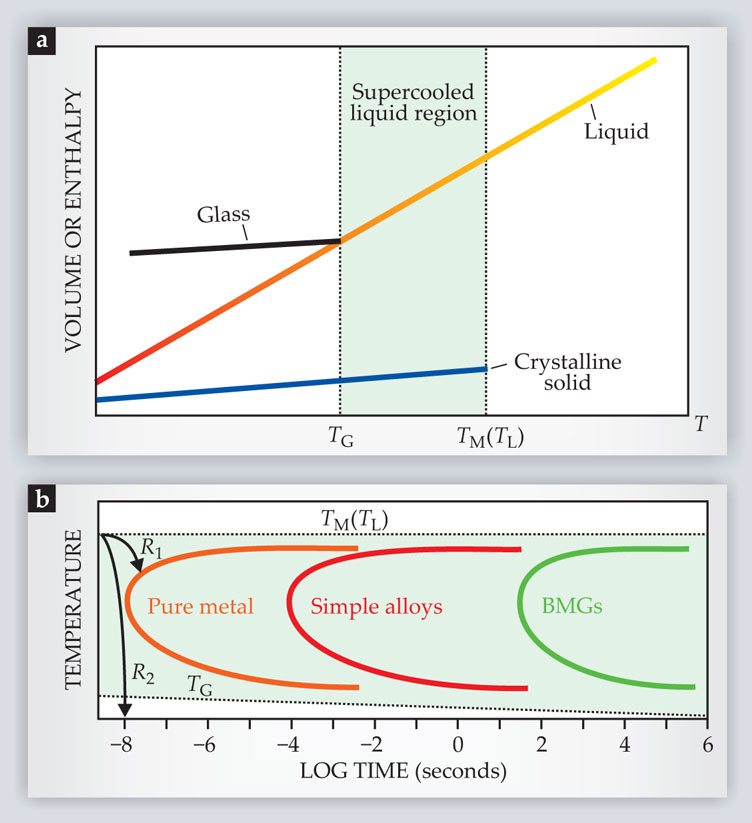
Creating a glass is akin to racing against a thermodynamic clock. The clock begins ticking when a liquid is cooled below its melting temperature T_M. Typically, as the supercooled liquid’s temperature decreases, so do its enthalpy and volume, as illustrated by the plot in figure 1a. (Water, which has a negative thermal expansion coefficient below 4 °C, is a notable exception.) At what’s known as the glass transition temperature T_G, the atoms in the liquid become so tightly packed that they can no longer easily rearrange themselves. In that glassy state, the system behaves like a solid, although liquid-like disorder is “frozen” into its structure. The challenge, then, is to supercool the liquid from T_M to T_G so fast that there’s no chance for a crystalline phase to nucleate and grow.

In materials that form localized chemical bonds—polymers, organics, and silica, to name a few—the race against crystallization is relatively easily won. In those systems, the crystalline lattice has both translational and bond-orientation order: To crystallize, molecules must find an appropriate place in the lattice and position themselves at just the right angle relative to neighbors. The collective rearrangements needed to fulfill both requirements proceed slowly enough that even moderate cooling rates suffice to supercool a liquid to T_G before it crystallizes.

Because metals are bound by freely shared conduction-band electrons, they have no orientational requirement and need only adopt translational order to crystallize. As a result, supercooled metals tend to crystallize quickly—so quickly that until about 60 years ago, it was thought infeasible to cool metals into a glassy state. We now know, however, that for certain metals—particularly alloys—under certain conditions, the thermodynamic clock ticks slowly enough to allow glass formation. It’s advantageous to cool the metal in an immaculate environment to reduce the number of impurities at which crystals might preferentially nucleate. But the chief breakthrough was recognizing that certain alloys have a dramatically lower propensity to crystallize than do pure metals. The discovery of such alloys has led to the fast-growing new class of materials known as bulk metallic glasses (BMGs).

In recent decades various research groups have discovered a wide range of bulk metallic glasses. Some are metal–metal alloys based on elements such as zirconium, copper, iron, and nickel; others combine metals with near-metalloids such as silicon, carbon, and phosphorus. Some metallic glasses are attractive for their magnetic properties; iron–boron glass, for example, is commonly used in distribution transformer cores. This article will focus on promising opportunities stemming from BMGs’ mechanical and thermodynamic properties. Specifically, BMGs exhibit a rare and tantalizing combination of traits: Their amorphous, defect-free microstructure makes them one of the strongest engineering materials known, and because they can occupy a peculiar thermodynamic middle ground between solid and liquid, they can be processed like plastics into nanoscale textures, seamless hollow containers, and other shapes that are impossible to make with traditional metals. (See this issue’s cover and the box on this page.)

A new class of glass

There’s no universally agreed-on answer to the question, What is a glass? It’s clear that a supercooled liquid exists in a metastable equilibrium: The crystalline solid state is energetically preferable, but the two states are separated by an activation barrier. That barrier is what enabled Daniel Fahrenheit, as early as 1724, to cool liquid water to nearly −10 °C without it freezing.

But it’s unclear how the glassy state is separated from the supercooled liquid in the energy landscape. Most evidence suggests that the states are not separated by an energy barrier and that the glass transition is not a true phase transition. Rather, the glass transition is widely thought to be a rate effect—a result of the material’s internal rate of relaxation becoming much slower than the laboratory cooling rate; in theory, a glass is always relaxing toward a supercooled liquid or crystalline state, it just does so at time scales far too long for us to observe.

Any liquid will vitrify, or solidify into a glass, if it’s cooled rapidly enough. (See figure 1b.) In the 1950s Werner Buckel and Rudolf Hilsch discovered that they could create amorphous solids by using vapor condensation to cool simple metallic melts at rates of approximately 10¹² K/s. Roughly 10 years later, Paul Duwez and coworkers found that certain fractional compositions of some alloys—Au₇₅Si₂₅, for example, where the subscript denotes the atomic percentage—are stable enough in the supercooled state to vitrify at cooling rates of order 10⁶ K/s. Nowadays we know that many alloys can form glasses when cooled at rates below 1000 K/s and as low as 1 K/s.

The bulkier a sample is, the more slowly its interior cools. So the critical cooling rate required for glass formation also determines the critical casting thickness—the maximum thickness for which the sample can be glass throughout. One can speak of a material’s glass-forming ability (GFA) as being either inversely proportional to its critical cooling rate or proportional to its critical casting thickness. By convention, a BMG is a metal with a critical casting thickness of at least 1 mm. The current record, set with Pd₄₀Ni₁₀Cu₃₀P₂₀, is 72 mm. ¹

Why the large disparity, more than 12 orders of magnitude, between the critical cooling rates of pure metals and those of BMG-forming alloys? To some extent, GFA is dependent on a metal’s specific chemical makeup, but the best glass-forming alloys do share some universal traits.

Packing matters

From the thermodynamic point of view, the driving force for crystallization can be represented as the difference between the Gibbs free energies of the crystalline solid (X) and supercooled liquid (L) phases, ΔG = (H_L − TS_L) − (H_X – TS_X). Here H is enthalpy, T is absolute temperature, and S is entropy. In the supercooled region, ΔG is always positive; the larger its magnitude, the greater the liquid’s propensity to crystallize and the lower its GFA. ²

From a rheological point of view, GFA can be related to viscosity η. The atoms in a supercooled liquid must do a significant amount of rearranging in order to crystallize, and that process unfolds more slowly in viscous fluids. All supercooled liquids exhibit an increase in viscosity as they are cooled toward the glass transition. In so-called strong liquids, viscosity grows gradually throughout the supercooled liquid region; in fragile liquids, it doesn’t appreciably increase until the temperature is very close to T_G. As a general rule, strong liquids have higher GFA than fragile ones.

Although the thermodynamic and rheological properties are often treated separately, they are in fact connected, as exemplified by the Adams–Gibbs relationship, η = Aexp{B/[TS_C(T)]}. Here, A and B are constants and S_C is configurational entropy. Furthermore, the favorable traits of small ΔG and high viscosity both have origins in the dense, efficient packing of atoms in the supercooled liquid.

Dense packing in the liquid phase is achieved through short-range order, with nearest-neighbor atoms organizing into crystalline shells that can extend up to nanometers across; ³ in metal–metal alloys, the shells are often icosahedral in structure. ⁴ Although such supercooled liquids are structurally disordered at macroscopic scales, they closely resemble crystalline solids at atomic scales. That resemblance manifests thermodynamically as similar Gibbs free energies of the liquid and solid phases, or small ΔG. And because tightly packed atoms have greater difficulty moving past one another, the ordered arrangements also lead to increased viscosity. In both respects, dense packing serves to enhance GFA—a conclusion that is supported by structural characterizations, indirect measurements, and simulations. ⁵

The search for new BMGs

The knowledge that dense packing improves GFA is, by itself, of little practical use for designing new and improved BMGs. For that task, heuristic guidelines and criteria are more helpful. In 1969 David Turnbull suggested that one might be able to predict an alloy’s GFA based on its T_G and its liquidus temperature T_L, the highest temperature at which a stable crystalline phase can form. (In a pure metal, T_L is equivalent to T_M; in an alloy, it serves roughly the same role as T_M during glass formation.) Based on empirical evidence, Turnbull proposed that any alloy with a ratio T_G/T_L exceeding 0.65 should form a BMG. The underlying idea is that the closer T_L is to T_G, the less one has to supercool the liquid to reach the glass transition and the easier it should be to do so before the liquid crystallizes.

The same principle suggests that an alloy with high GFA is likely to be one with a large, negative heat of mixing—that is, one whose free energy in the mixed state is much less than that of its individual component metals. For such alloys, T_L is small compared with the average T_M of the constituent metals.

A limitation of Turnbull’s criterion is that it doesn’t account for what’s known as nonpolymorphic crystallization. Most alloys, particularly those that readily form metallic glasses, can assume a variety of crystalline structures whose chemical compositions differ from that of the liquid phase. As a consequence, crystallization creates local concentration gradients and, limited by long-range diffusion, occurs at a slower rate that facilitates glass formation.

To account for nonpolymorphic effects, Turnbull’s criterion can be modified to include the crystallization temperature, the temperature at which the amorphous solid crystallizes when heated. That temperature captures certain kinetic aspects of crystal formation, although not necessarily of the crystalline phases that pertain to GFA. ⁶

Nonpolymorphic crystallization and dense packing are the basis of Lindsay Greer’s confusion principle, a guideline for achieving high GFA. The confusion principle calls for metal combinations that can form complex and vastly different crystalline phases, which enhances nonpolymorphism, and that are size polydisperse, which increases packing density. Akihisa Inoue pointed out in 2001 that a dense liquid-phase packing can typically be orchestrated by choosing atoms with a size difference of 12% or more, so that the smaller atoms can fit in the interstices of the larger ones.

Electronic effects have also been invoked to explain GFA. ⁷ Some studies suggest that GFA is highest for alloys containing roughly 1.5 conduction-band electrons per atom. However, that correlation has not been widely confirmed, and more work is required to conclude its importance to GFA.

Strong and sometimes tough

The failure behavior of a crystalline solid is predominantly a function of the quantity, distribution, and nature of its dislocations, the defects in its crystalline lattice. But since metallic glasses are amorphous, they lack dislocations and the associated slip planes. As a result, they display some unusual mechanical properties. ⁸

Bulk metallic glasses are exceptionally strong and elastic, meaning they can withstand large stresses without permanently losing their shape. In fact, BMGs are among the strongest engineering materials known and are typically stronger than steel (see figure 2). When a BMG does fail, however, it tends to do so catastrophically. Crystalline solids exhibit strain hardening: Dislocations preferentially form in locations of enhanced shear, and those dislocations locally harden the material and thereby relocate shear away from the original source. That redistribution of stress throughout the bulk leads to a relatively homogenous deformation. Because BMGs have no dislocations, they tend to localize shear in narrow, roughly 10-nm bands (see figure 3a). The high shear rate generates heat that causes the material in the band to dilate and weaken, which leads to a lower shear resistance and an even higher shear rate. Hence, a strain-softening instability develops.

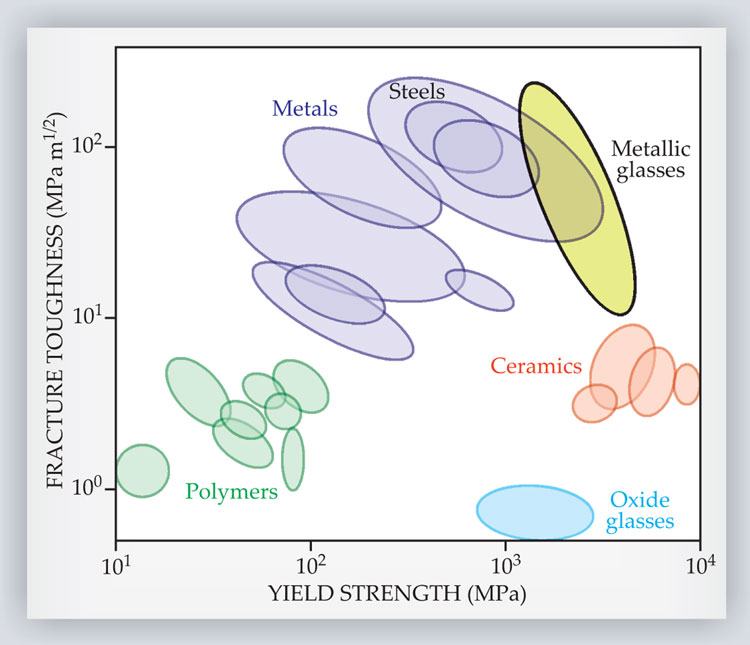
Another important measure of mechanical viability is toughness, a material’s ability to resist the propagation of cracks. As shown in figure 2, BMGs exhibit large variation in this category: Some are brittle, in that small cracks easily grow into large fractures; others are impressively tough. ⁹ The variation can be related to materials’ relative elastic stiffness under shear and pressure. ¹⁰ BMGs that are more susceptible to elastic shear than to pressure—those with a low shear modulus relative to the bulk modulus—tend to be the toughest. Under stress, they form propagating shear bands that dissipate energy and lower the probability for a crack to form (see figure 3b). Recent evidence suggests, however, that other factors—such as the cooling rate and processing conditions—also play a part. ¹¹

Ductility, the ability to plastically deform—to bend without breaking, for instance—is a trouble area for BMGs. Typically, BMGs are ductile only if their thickness is less than 10 times the critical crack length—the length of the largest crack the material can withstand before significantly weakening. For most BMGs, the critical crack length is around 100 µm, so achieving bending ductility in a BMG requires casting thicknesses of 1 mm or less ¹² (see figure 3c).

Thermoplastic forming

The above discussion of mechanical properties applies to BMGs at room temperature and well below T_G, which for most BMGs falls in the range 150–350 °C. As Frans Spaepen explained in 1977, however, BMG properties are highly and nonlinearly temperature dependent: If a BMG is heated to near T_G and subjected to gentle strain, it begins to behave less like a solid and more like a liquid. ¹³

When reheated to the supercooled liquid region just above T_G, a BMG begins to slowly relax into a liquid and, eventually, into a crystalline solid. Scientifically, that regime is interesting because it enables fundamental studies of rheology, diffusion, and thermodynamics of highly viscous melts far from equilibrium. ² Technologically, it gives rise to unique metal-processing opportunities.

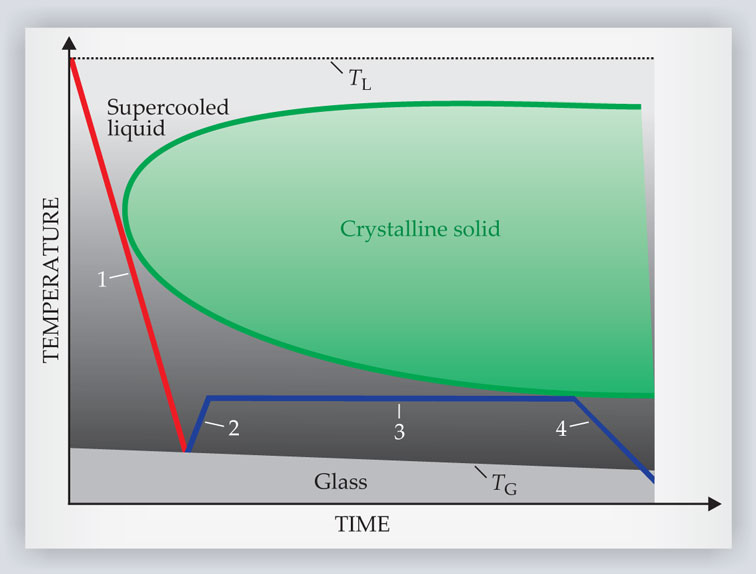
In the supercooled liquid region, BMGs can be shaped and molded much like plastics via a process known as thermoplastic forming. The typical thermoplastic forming protocol is illustrated in figure 4. First, the alloy melt is cooled to the glass transition to form a BMG. Next, the BMG is reheated into the supercooled liquid region, where it gradually softens. A stress is then applied to form the material into the desired shape. That stress may take the form of, say, compression, injection molding, extrusion, hot rolling, blow molding, or wire drawing. Finally, the alloy is recooled below T_G.

There is a limited, temperature-dependent window of time, t_cryst(T), in which to shape and form the BMG before it crystallizes. Also dependent on temperature is the material viscosity η(T), which determines the ease with which the BMG will deform during processing. Thus, for a given set of conditions, the total amount of deformation that can be achieved in a single round of thermoplastic forming is given by a temperature-dependent quantity known as formability, F(T) = t_cryst(T)/η(T).

Evidence shows that formability increases with temperature; as temperature rises, the penalty of smaller available processing time is overcompensated by a simultaneous drop in viscosity. Thus thermoplastic forming is usually carried out at the highest practically accessible processing temperature. To that end, the development of heating techniques that can achieve high temperatures quickly, at time scales much shorter than t_cryst, has been an important breakthrough.

Thermoplastic forming was first demonstrated on metallic glasses in 1978, but the recent discovery of highly formable BMGs has accelerated its development. ¹⁴ The technique has been successfully used to pattern and shape BMGs on length scales ranging from subnanometers to meters ¹⁵ (see figure 5).

The road ahead

Bulk metallic glasses exhibit material attributes that were previously thought to be mutually exclusive. Conventional metals are strong but challenging to process—in their solid state, they are too hard; in their liquid state, too soft. Thermoplastics are easily processed but lack strength. Because BMGs are both strong and easily processed, they open the door to a variety of intriguing applications.

A key feature of BMGs is their lack of an intrinsic length scale. In crystalline metals, the characteristic length scale is set by the grain size, typically between 50 nm and 50 µm. In polymers, the intrinsic length scale is set by the chain length, typically several nanometers. But since BMGs have amorphous microstructure, they can be shaped at almost arbitrarily small length scales. For instance, catalytically active BMGs containing palladium or platinum can be formed with nanometer-sized features, which would make them attractive for use in fuel cells, batteries, and sensors, where large surface area is important. ¹⁶

Another prospective application is imprinting, or embossing, particularly on the micro- and nanoscale. There the BMG can serve either as a hard and durable imprint tool, if used at T ≪ T_G, or as a soft imprint material, if used at T ≈ T_G. The most promising scenario is to use BMGs as tools to imprint thermoplastic materials.

To realize the vast potential of BMGs, today’s materials scientists still have some limitations to overcome. One is that suitable ductility can currently only be achieved in alloys that are hazardous to human health, expensive, difficult and unreliable to process, or otherwise impractical. And even then, the material length scale must be small. Achieving ductility in technologically interesting BMGs will require a better understanding of the underlying physics. Computational methods can be expected to play a major role in that effort.

Another limitation is material costs. Even the most economical BMGs comprise materials that cost around $100/kg, while common steels average about $1/kg. The price currently limits BMGs to high-value-added applications for which processing costs, not materials, are the limiting economic factor. Such applications include electronic casings, medical implants and devices, catalysts, watch cases and components, microelectromechanical resonators and sensors, imprint tools, and jewelry.

Current BMG development is based on scientific intuition rather than rationale. Advances are realized through a time-intensive strategy of trial and error; it takes almost an entire day to fabricate and characterize just one alloy composition. As a consequence, only a minute fraction of potential BMG-forming compositions have been explored thus far. To investigate the vast remaining phase space, more efficient techniques, such as combinatorial and high-throughput methods, are required.

Computational methods can be used to help unravel the structure of known BMGs, but they aren’t yet efficiently used to develop new ones. In part, that’s because molecular dynamics simulations of glass formation and crystallization are difficult and time consuming: The longest realizable molecular simulations are still many orders of magnitude too short to simulate glass formation or crystallization at realistic cooling rates. In addition, proper treatment of chemical bonding must take into consideration quantum effects, which further increase computational demands.

Advances in data mining, density functional theory calculations, and other computational methods might speed the development of BMGs, but even those methods are unsuited to determine states of metallic glasses that are realized under experimental conditions, since for any given alloy there is virtually an unlimited number of possible amorphous configurations. Instead of molecular-dynamics-style approaches, efficient computational strategies might draw on analytical understanding of correlations—for instance, between the energies of an alloy’s various crystalline phases and its GFA.

Bulk metallic glasses have found a growing number of applications in recent decades. But whether, and at what pace, BMGs continue to proliferate will hinge on the advancement of thermoplastic-based fabrication techniques for large-scale industrial use and the scientific community’s ability to find next-generation BMGs for the exciting applications that await.

More about the cover images

The objects seen here and on this issue’s cover exemplify the broad range of potential uses and applications for bulk metallic glasses (BMGs). Shown, from left to right and top to bottom, are 100-nm-thick platinum BMG nanorods; micron-sized dendrites, formed by electrochemical processing of a BMG; a millimeter-sized metallic “wineglass,” which can serve as an ultralow-loss mechanical resonator; a miniature mechanical part with features that vary in size from a few microns to several hundred microns (ref. ); a seamless, hollow watch case formed in less than 20 seconds via blow-molding (ref. , J. Schroers et al.); catalytic nanofibers 50 nm in diameter and 10 µm long; a multicolored optical pattern embossed on a bulk metallic glass surface (ref. ); miniature tweezers 2 mm in length, fabricated through thermoplastic forming (ref. ); and a blow-molded BMG container. (All images are courtesy of the Schroers lab; montage designed by Miriam Schroers.)