Brownian Motors

A great challenge for the burgeoning field of nanotechnology is the design and construction of microscopic motors that can use input energy to drive directed motion in the face of inescapable thermal and other noise. Driving such motion is what protein motors—perfected over the course of millions of years by evolution—do in every cell in our bodies. ¹

To put the magnitude of the thermal noise in perspective, consider that the chemical power available to a typical molecular motor, which consumes around 100–1000 molecules of adenosine triphosphate (ATP) per second, is 10⁻¹⁶ to 10⁻¹⁷ W. In comparison, a molecular motor moving through water exchanges about 4 × 10⁻²¹ J (the thermal energy kT at room temperature) with its environment in a thermal relaxation time of order 10⁻¹³ s. Thus, a thermal noise power of about 10⁻⁸ W continually washes back and forth over the molecule. That power, which, according to the second law of thermodynamics cannot be harnessed to perform work, is 8–9 orders of magnitude greater than the power available to drive directed motion. For molecules, moving in a straight line would seem to be as difficult as walking in a hurricane is for us. Nonetheless, molecular motors are able to move, and with almost deterministic precision.

Inspired by the fascinating mechanism by which proteins move in the face of thermal noise, many physicists are working to understand molecular motors at a mesoscopic scale. An important insight from this work is that, in some cases, thermal noise can assist directed motion by providing a mechanism for overcoming energy barriers. In those cases, one speaks of “Brownian motors.” ² In this article, we focus on several examples that bring out some prominent underlying physical concepts that have emerged. But first we note that poets, too, have been fascinated by noise; see box 1.

Bivalves, bacteria, and biomotors

Bacteria live in a world in which they are subject to viscous forces large enough that the inertial term $m\dot{\nu }$ in Newton’s equation of motion can be safely ignored. The motion of the bacteria, governed by those viscous forces, is very different than the inertia-dominated motion that we know from everyday experience. Edward Purcell, in his classic article “Life at Low Reynolds Number,” highlighted that difference by formulating what has come to be known as the scallop theorem. ³

A scallop is a bivalve (a mollusk with a hinged shell) that could, in principle, move by slowly opening its shell and then rapidly closing it. (In fact, the scallop’s method of locomotion is somewhat different.) During the rapid closing, the scallop would expel water and develop momentum, allowing it to glide along due to inertia. A typical scallop has a body length a of about a centimeter and propels itself at a speed v of several cm/s, that is, at several times its length per second. Thus, the Reynolds number, $R=a\nu \rho /\eta$ (a dimensionless parameter that compares the effect of inertial and viscous forces), is about 100, where ρ is the density of the fluid (for water, the density is 1 g/cm³) and η is the fluid’s viscosity (for water, about 10⁻² g/(cm·s)).

For organisms a few thousand times smaller than a scallop, also moving at several body lengths per second, the Reynolds number is much less than one. In that case, the glide distance is negligible. Because the motion generated by opening the shell cancels that produced on closing the shell, a tiny “scallop” cannot move. The mathematical reason is that motion at low Reynolds number is governed by the Navier–Stokes equation without the inertial terms, $-\nabla p+\eta {\nabla }^2\nu =0$ . Because time does not enter explicitly into the equation, the trajectory depends only on the sequence of configurations, and not on how slowly or rapidly any part of the motion is executed. Hence, any sequence that retraces itself to complete a cycle—and that is the only type of sequence possible for a system such as a “scallop” with just one degree of freedom—results in no net motion.

With typical lengths of about 10⁻⁵ m and typical speeds of some 10⁻⁵ m/s, bacteria live in a regime in which the Reynolds number is quite low, about 10⁻⁴. Thus, bacteria must move by a different mechanism than that used by a “scallop.” Our purpose is not to investigate how actual bacteria move (see the article “Motile Behavior of Bacteria” by Howard C. Berg in Physics Today, January 2000, page 24 ) but to examine generic mechanisms by which locomotion at low Reynolds number is possible, with an ultimate focus on molecule-size Brownian motors.

Purcell described several locomotion mechanisms, all of which pertain to motion induced by cyclic shape changes in which, unlike the scallop’s cycle, the sequence of configurations in one half of the cycle does not simply retrace the sequence of configurations in the other half. Here, we consider the two mechanisms shown in figure 1, the corkscrew and the flexible oar.

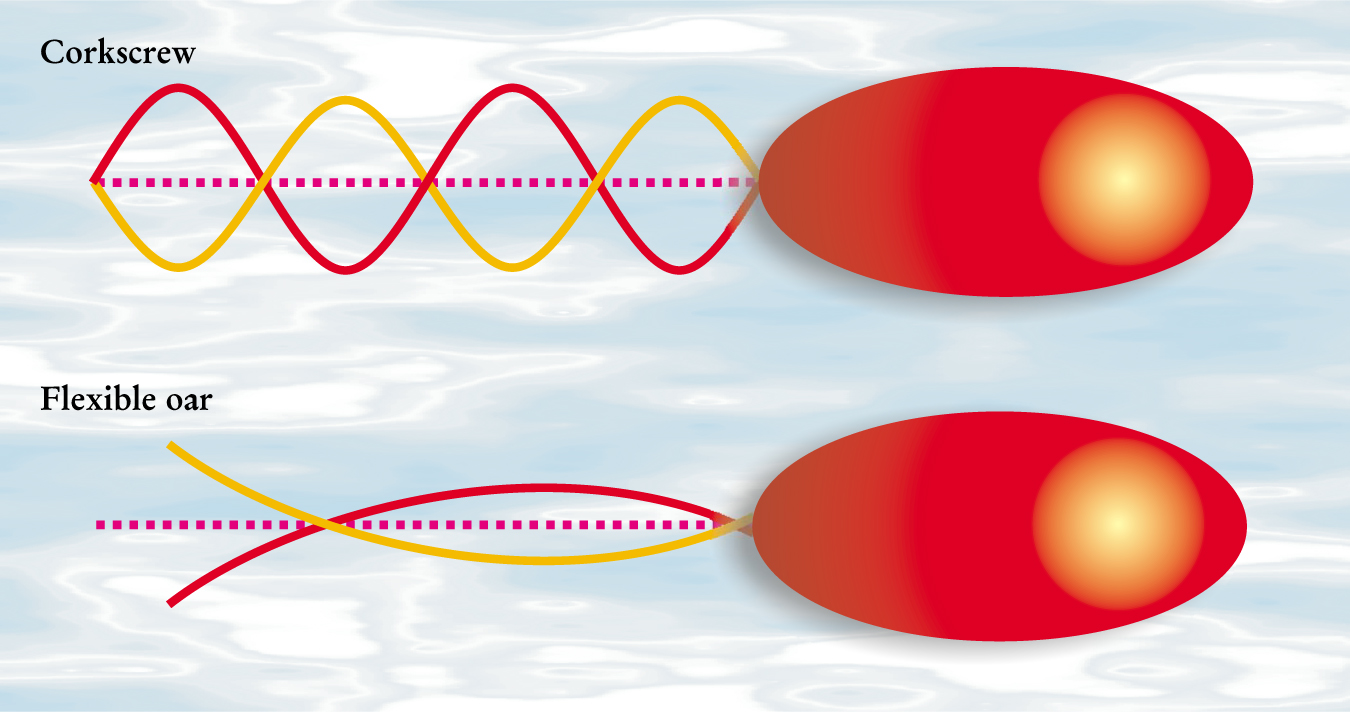
The two mechanisms shown have different symmetries. The corkscrew mechanism avoids retracing its steps by its chirality. At low frequency, the bacterium moves a fixed distance for each complete rotation of the chiral screw about its axis. Thus, the velocity is proportional to the frequency. Reversing the sense of corkscrew rotation reverses the bacterium’s motion. Slow enough rotation produces motion with essentially no dissipation, so we call the corkscrew an adiabatic mechanism.

On the other hand, the flexible oar relies on the internal relaxation of the oar curvature to escape the scallop theorem. At low frequency, the amplitude of the bending of the oar is proportional to the frequency and the velocity is thus proportional to the square of the frequency. Because, in this case, relaxation and dissipation are essential, the flexible oar is an example of a nonadiabatic mechanism. ⁴

The role of noise

The mechanisms in figure 1 illustrate how self propulsion at low Reynolds number is possible. A new problem arises, however, when particles have lengths characteristic of molecular dimensions, 10⁻⁸ m or so.

In that case, diffusion caused by thermal noise (Brownian motion) competes with self-propelled motion. The time to move a body length a at a self-propulsion velocity v is a/v, while the time to diffuse that same distance is of the order $a^2/D$ . Here, the diffusion coefficient D is given in terms of particle size, solution viscosity, and thermal energy by the Stokes–Einstein relation $D=kT\left(6\pi \eta \alpha \right)$ . At room temperature, and in a medium whose viscosity is about that of water, a bacterium needs more time to diffuse a body length than it does to “swim” that distance. For smaller molecular-sized particles, however, a body length is covered much faster by diffusion. For molecular motors, unlike bacteria, the diffusive motion overwhelms the directed motion of swimming.

A solution widely adapted in biology is to have the motor on a track that constrains the motion to essentially one dimension along a periodic sequence of wells and barriers. ⁵ The energy barriers significantly restrict the diffusion. Thermal noise plays a prominent constructive role by providing a mechanism, thermal activation, by which motors can escape over the barriers. ⁶ (See also the article “Tuning in to Noise” by Adi R. Bulsara and Luca Gammaitoni in Physics Today, March 1996, page 39 .) The energy necessary for directed motion is provided by appropriately raising and lowering the barriers and wells, either via an external time-dependent modulation or by energy input from a nonequilibrium source such as a chemical reaction.

A simple Brownian motor

Figure 2 shows a simple example of a Brownian motor, in which a molecule-sized particle moves on an asymmetric sawtooth potential. Such an asymmetric profile is often called a ratchet after the beautiful example given by Richard Feynman in his Lectures on Physics, volume I, chapter 46 (Addison-Wesley, 1963). Feynman used his ratchet to show how structural anisotropy never leads to directed motion in an equilibrium system. But in the nonequilibrium system depicted in figure 2, the potential’s cycling—which provides the energy input—combines with structural asymmetry and diffusion to allow directed motion of a particle, even against an opposing force. (An excellent simulation of the Brownian motor is at the Web site http://monet.physik.unibas.ch/~elmer/bm/ .)

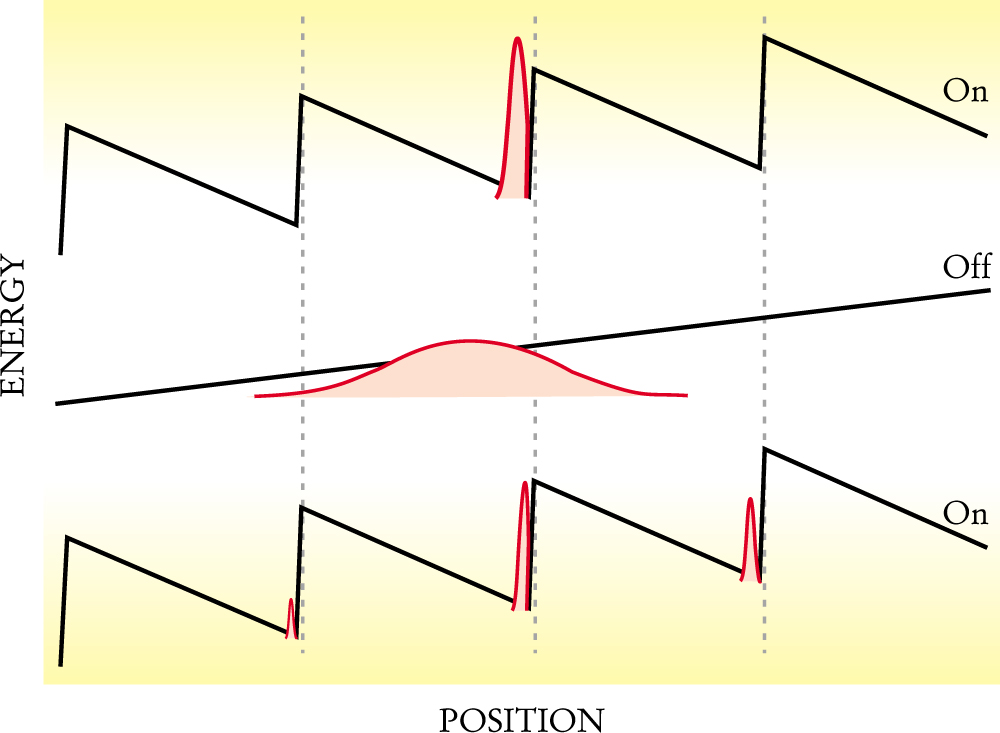
For biological motors on a track, one might expect the length a and track period L to be of molecular size and the viscous drag coefficient to be around 10⁻¹⁰ kg/s, somewhat higher than that in water due to friction between the motor and track. If the potential is switched on and off with a frequency of 10³ Hz, consistent with the rate of ATP hydrolysis by many biological motors, the induced velocity is about 10⁻⁶ m/s and the force necessary to stop the motion is approximately 10⁻¹¹ N: The velocity and force estimates are both consistent with values obtained from single-molecule experiments on biological motors. ¹ (See also the article “The Manipulation of Single Biomolecules” by Terence Strick, Jean-François Allemand, Vincent Croquette, and David Bensimon in Physics Today, October 2001, page 46 ).

An effect analogous to the directed motion caused by cyclically turning a potential on and off can be demonstrated for particles moving on a fixed asymmetric track, such as a sawtooth etched on a glass slide. ⁷ The energy input driving the directed motion is provided by cyclically varying the temperature between high and low values. At high temperatures the particles diffuse, but when the temperature is low the particles are pinned in the potential wells. Because of the asymmetry of the track, the fluctuations over time between hot and cold cause the particles to move, on average, over the steeply sloped, shorter face of the etched sawtooth.

In the scheme depicted in figure 2, the fuel is the energy supplied by turning the potential on and off. The track, or substrate, is the lattice on which the particle moves. The particle is the motor—the element that consumes fuel and undergoes directional translation. The model illustrates the two main ingredients necessary for self-propelled motion at low Reynolds number: symmetry breaking and energy input. The particle in the illustrated scheme is a true Brownian motor, because without thermal noise to cause Brownian motion, the mechanism fails. ⁸

The ratchet in figure 2 mimics a Brownian motor first proposed in 1992 by Armand Ajdari and Jacques Prost working at the Ecole Supérieure de Physique et de Chimie Industrielles in Paris. ⁹ They envisioned a situation in which turning on and off an asymmetric electric potential would provide a means for separating particles based on diffusion.

Several groups explored that possibility in various ways during the mid-to-late 1990s. ¹⁰ In 1994, Ajdari and Prost, along with colleagues Juliette Rousselet and Laurence Salome, constructed a device for moving small latex beads unidirectionally in a non-homogeneous electric potential that was turned on and off cyclically. About a year later, Albert Libchaber and colleagues at Princeton University and at NEC Research Institute Inc, made an optical ratchet. By modulating the height of the barrier on an asymmetric sawtooth fashioned from light, they could drive a single latex bead around a circle. Most recently, Joel Bader and colleagues at CuraGen Corp constructed a device for efficient separation of DNA molecules using interlocking combed electrodes with an asymmetric spacing between the positive and negative electrodes.

General description

When we considered the scallop theorem and the devices bacteria use to evade it, we focused on physical changes—the opening and closing of a scallop’s shell, the turning of a corkscrew, and the waving of a flexible flagellum. In a general mathematical description of motion at low Reynolds number, a time-dependent potential corresponds to the changes in shape that we discussed earlier.

Imagine a particle constrained to move on a line, with a spatially periodic time-modulated potential V(x, t). The particle is governed by the equation of motion $$m\dot{\nu }+V^{\prime }\left(x,t\right)=-\gamma \nu +\sqrt{\left(2kT\gamma \right)}\xi \left(t\right),$$ where the prime denotes a spatial derivative and $\gamma =6\pi \eta a$ is the viscous drag coefficient. The left-hand side of the equation of motion describes the deterministic, conservative part of the dynamics, and the right-hand side accounts for the effects of the thermal environment—viscous damping and a fluctuating force modeled by thermal noise ξ(t). If both inertia and noise are negligible, the equation of motion may be approximated as $V^{\prime }\left(x,t\right)=-\gamma \nu$ : Explicit time dependence enters only through V′(x, t). Thus, the pattern of motion is independent of whether the modulations occur rapidly or slowly. If, as is the case for a standing-wave modulation, the changes are such that the path in the second half of the cycle retraces those of the first, then the velocity must also retrace its steps. That retracing is irrespective of the amplitude, waveform, or frequency of the modulation.

For Brownian motors, however, there is ineluctable and significant thermal noise, which changes the situation dramatically. Because noise provides a mechanism for relaxation—an internal response of the system to a change in the external parameters—a single external degree of freedom can combine with the internal dynamics to escape the scallop theorem and yield directed motion, as in the scheme depicted in figure 2. In boxes 2 and 3, we have worked out a second illustrative scheme in detail and discussed the relationship of that scheme with the principle of detailed balance.

As illustrated in the first of those boxes, the net current (an appropriately normalized average velocity) due to modulation of the potential can be broken into two contributions. One is a purely geometric term corresponding to motion similar to that induced by a slow traveling-wave modulation. That term depends only on the two external parameters that define the modulation and describes the reversible part of the transport. Similar in spirit to the Berry, or geometric, phase in quantum mechanics (see the article “Anticipations of the Geometric Phase” by Michael Berry in Physics Today, December 1990, page 34 ), that first term corresponds to the adiabatic transport mechanism described by David Thouless and recently used by Charles Marcus and his colleagues to pump electrons through a quantum dot with essentially no energy dissipation (see Physics Today June 1999, page 19 ). ¹¹

The second term corresponds to the dissipative part of the transport and is the term typically associated with the ratchet effect: In the on-off ratchet shown in figure 2, the average of the adiabatic term is zero—all of the net transport is described by the irreversible term. The dissipative nature of the mechanism corresponding to the irreversible term means that even random fluctuations such as those that might arise from a simple two-state nonequilibrium chemical reaction can drive transport. ¹²

Two-dimensional ratchets

The Brownian motors we have considered so far have been confined to one spatial dimension and subject to time-varying potentials. One can develop a sharper intuition for Brownian ratchets by mapping time-modulated potentials into static, 2D potentials: $\left(x/L,\omega t\right)\to \left(x/L_x,y/L_y\right)$ . The modulation, instead of being characterized by functions of time, is then characterized by functions of the coordinate y. ^13,14 The nonequilibrium features implicit in the original external temporal modulation are introduced by external forces in the x or y directions.

The resulting 2D potentials yield two classes of devices distinguished by symmetry. In one class, proposed by Tom Duke and Bob Austin, symmetry is broken in both coordinates in the sense that changing the sign of either x or y changes the potential. A member of this symmetry class is illustrated in figure 3(a), which also shows the response of particles to forces in the up and down directions. Note that changing the direction of the force changes the direction of the resulting velocity. In general, for potentials with broken symmetry in both coordinates, to leading order, the x-component of current resulting from a force in the y direction is the same as the y-component of current resulting from the same magnitude force in the x direction. Generally, if the force in the, say, x direction is zero, current in both the x and y directions is proportional to the force in the y direction.

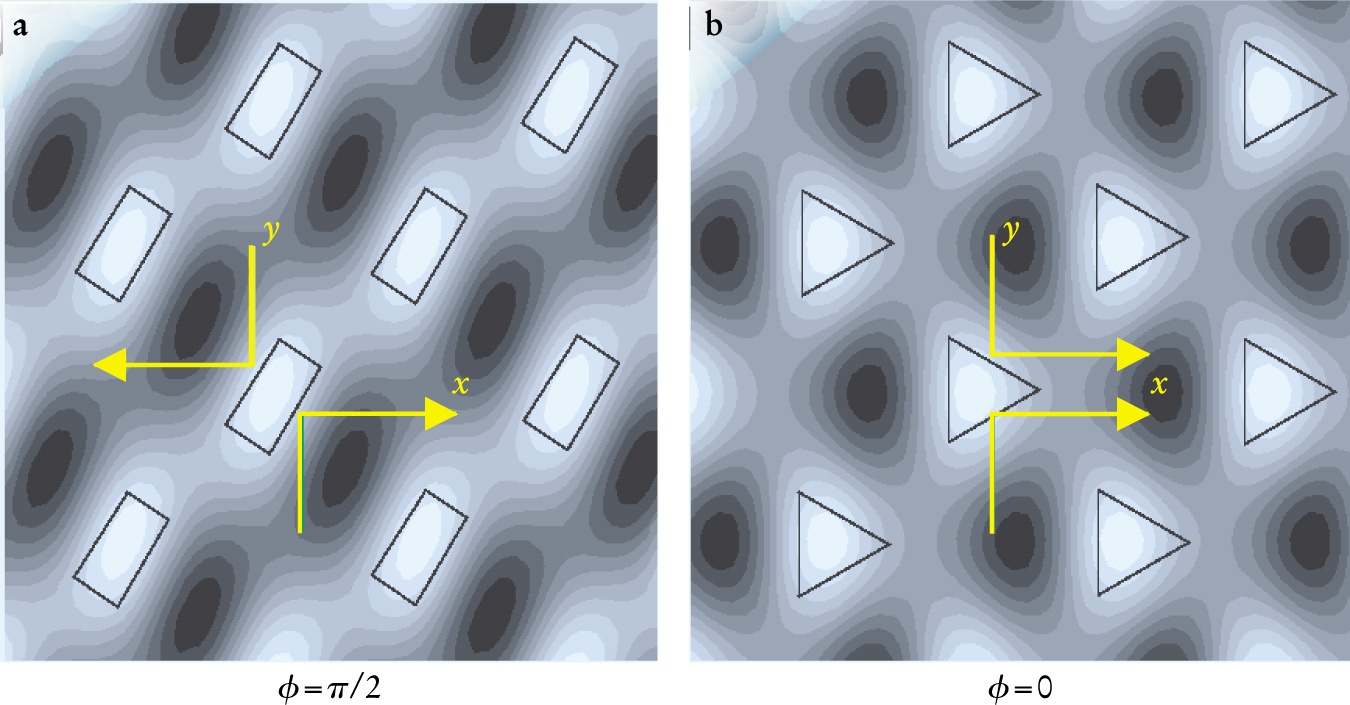
In the second class of devices, suggested by Imre Derényi and Dean Astumian and by Axel Lorke and colleagues, symmetry is broken in only one coordinate. Figure 3(b) shows a member of this class, with broken symmetry in the x coordinate. The figure also shows that a force up or down induces flow to the right; by symmetry, a force in the x direction induces no net flow in the y direction. An algebraic manifestation of those responses to force is that, to lowest order, the particle current in the x direction is proportional to the square of the y component of force.

An advantage of the second class is that an oscillating force in the y direction can drive unidirectional motion in the x direction, thus allowing devices to be much smaller. One can achieve good lateral separation without particles traveling very far vertically. Combining systems with different symmetry properties may make it possible to tailor a potential for the most effective separation in a given system.

So far, only the first symmetry class has been applied experimentally for particle separation, ¹³ but the second has been realized for ratcheting electrons that move ballistically through a maze of antidots. ¹⁴ Electrons in a 2D square array of triangular antidots move in a potential similar to that shown in figure 3(b). When irradiated by far-infrared light, the electrons are shaken and crash against the antidots rather like balls hitting the obstacles on a pinball table. The electrons are then funneled into the narrow gaps between the antidots, thereby yielding a well-directed beam. Indeed, one observes a net photovoltage between source and drain—merely the expected ratchet effect that turns an AC source into a DC one.

Two-dimensional ratchets open a doorway to wireless electronics on the nanoscale. For example, different orientations of asymmetric block structures may allow for the guiding of several electron beams across each other. As suggested by Franco Nori and his collaborators at the University of Michigan, specially tailored 2D potentials, combined with a source of thermal or quantum noise, can provide a lens for focusing or defocusing electrons, much as optical lenses manipulate light. ¹⁵

Ratchets in the quantum world

Symmetry breaking and the use of noise to allow randomly input energy to drive directed motion can also be exploited when quantum effects play a prominent role. An especially appealing possible application is the pumping and shuttling of quantum objects such as electrons along previously selected pathways without the explicit use of directed wire networks or the like.

One of the most important features of quantum transport not present in the classical regime is quantum tunneling. Tunneling provides a second mechanism—the first being the thermal activation exploited for classical ratchets—for a particle to move among energy wells. Heiner Linke and colleagues took brilliant advantage of the two mechanisms in designing a quantum ratchet showing a current reversal as a function of temperature (see figure 4). ¹⁶ Peter Hänggi and coworkers applied quantum dissipation theory to a slowly rocked ratchet device to theoretically anticipate such a current reversal. ¹⁷

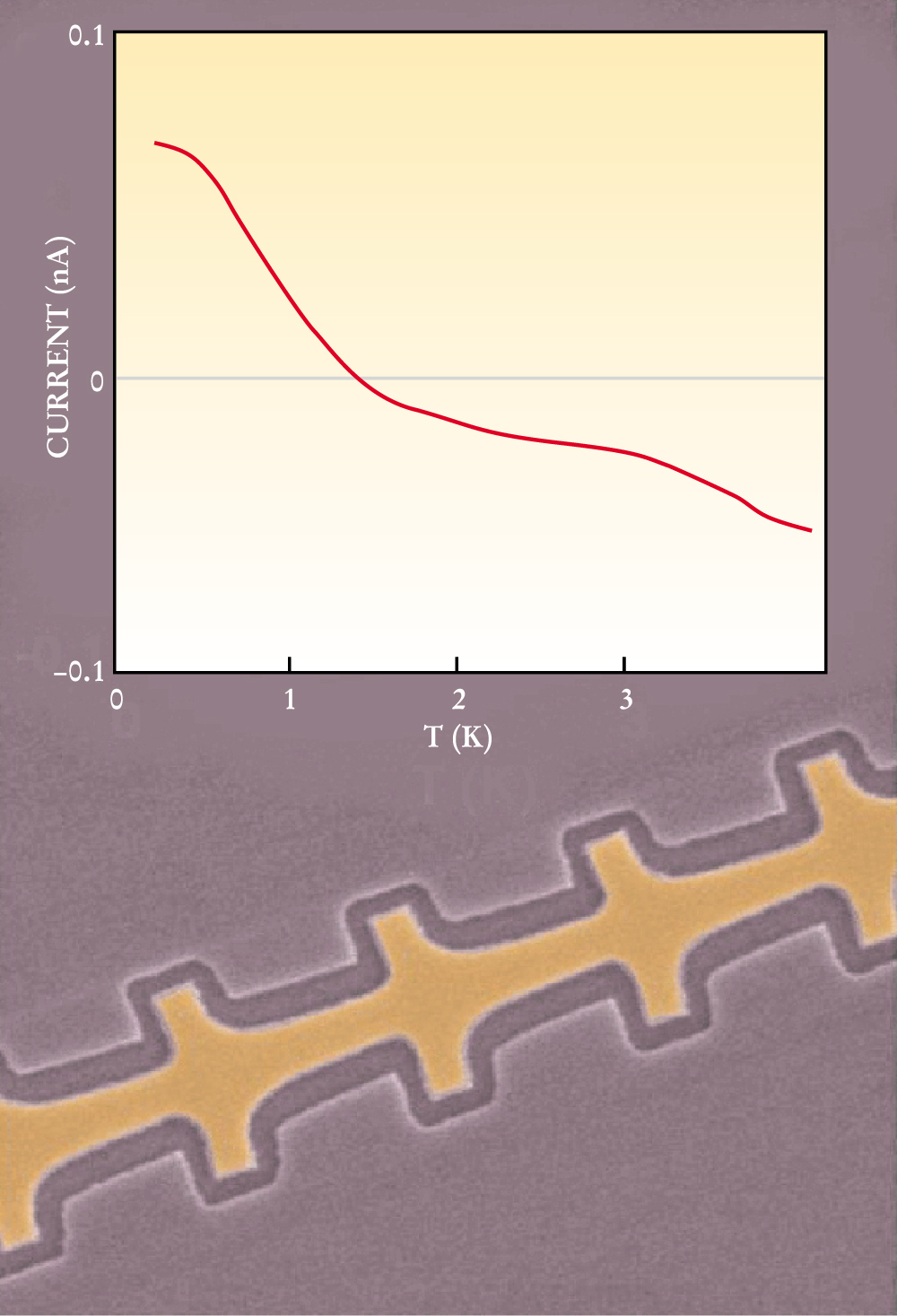
Using electron beam lithography, Linke and coworkers constructed an asymmetric electron waveguide within a 2D sheet of electrons parallel to the surface of an aluminum-doped gallium arsenide/gallium aluminum arsenide heterostructure. The device comprised a string of funnel-shaped constrictions, each of which forms an asymmetric energy barrier for electrons traveling along the waveguide. A slow (192 Hz), zero-average, periodic, square-wave voltage was applied along the channel to rock the ratchet potential. In other words, electrons traveling through the waveguide were subjected to a uniform perturbing force that periodically switched direction.

At low temperature, tunneling predominates. The barriers are narrowed when the force is to the right and widened when the force is to the left, thus inducing electron current to the right. Because of the asymmetry, the rocking produces a net current. At high temperatures, where thermal activation predominates, electrons move preferentially over the gentle slope of the potential. That movement leads to an electron current to the left. Moreover, the device functions as a heat pump even when the temperature is set to the value that produces no net electrical current: The thermally activated current is predominantly due to electrons in higher-energy states whereas the tunneling current is mainly due to electrons in the lower-energy states. ¹⁷

Quantum ratchets are potentially useful in any number of tools such as novel rectifiers, pumps, molecular switches, and transistors. Some day, devices built with quantum ratchets may find their way into practical applications.

Perspective and overview

A Brownian motor is remarkably simple: The essential structure consists of two reservoirs, A and B, with two pathways between them. (In the example of box 2, the two pathways are defined by whether the potential barrier overcome is to the left or right of well A.) By periodically or stochastically altering both the relative energies of the reservoirs and the “conductances” of the pathways between them, with a fixed relationship between the two modulations, one can arrange that transport from A to B is predominately via one pathway and transport from B to A is via the other pathway. Depending on the topology, the induced particle motion could be realized as directed transport along a circle or a line, transfer of microscopic cargo or electrons between two reservoirs, or coupled transport in two dimensions.

In micro- and nanoscale materials such as polymers or mesoscopic conductors, thermal activation and quantum mechanical tunneling are mechanisms for overcoming energy barriers (incidentally introducing nonlinearity). ⁶ In addition, the multiple time scales inherent in complex systems allow the necessary correlations between the fluctuations of the conductances and energies to emerge spontaneously from the dynamics of the system. In those cases, noise plays an essential or even dominating role: It cannot be switched off easily and, moreover, in many situations, not even the direction of noise-induced transport is obvious! Because the direction and speed of transport depend on different externally controllable parameters—temperature, pressure, light, and the phase, frequency, and amplitude of the external modulation—as well as on the characteristics of the potential and on the internal degrees of freedom of the motor itself, synthetic Brownian molecular motors can be remarkably versatile. ¹⁸

In the microscopic world, “There must be no cessation / Of motion, or of the noise of motion” (box 1). Rather than fighting it, Brownian motors take advantage of the ceaseless noise to move particles efficiently and reliably.