An atomic physics perspective on the kilogram’s new definition

Although often the bane of freshman physics students, units of measure are important for applications from commerce to fundamental physics. The current Système International (SI) units emerged early in the French Revolution to unify and promote égalité (“equality”) in commerce. Over the past two centuries, major changes and updates to SI units have occurred, but the redefinitions introduced on 20 May 2019 were the biggest conceptual transformation in metrology since the French Revolution.

All prototype-based definitions have now been replaced with ones based on the cesium atom and fundamental constants. (See the article by David Newell, Physics Today, July 2014, page 35 .) The most profound change in units is the kilogram, which is no longer defined by the artifact in Paris but by the fixed value of Planck’s constant $h$ = 6.626 070 15 × 10⁻³⁴ kg m²/s. The new definition became possible when the best two measurements of $h$, the Kibble balance and the silicon spheres, reached an accuracy similar to the mass drift of the urkilogram over 130 years. At that point, the General Conference on Weights and Measures (CGPM), the SI’s governing body, decided to define $h$ as its precisely measured numerical value, which then defines the kilogram ^{1 , 2} in combination with the speed of light $c$ and the Cs hyperfine frequency ${\nu }_{\mathrm{Cs}}$. Realizations of the kilogram standard, whether conceptual or practical, connect the mechanical or relativistic energy of a particle or object to a frequency, which is compared to an atomic frequency standard. In that way, atomic physics is central to the new definition of the kilogram.

From artifacts to fundamental constants

Over time, physicists have defined and redefined units based on natural objects, then objects of human creation and scale, and finally microscopic objects paired with fundamental constants. For example, the meter was first defined as one ten-millionth of the distance from the equator to the North Pole. In 1799 that standard was replaced by a manufactured prototype meter bar, which was more precise. But the accuracy was still limited to 10⁻⁷, and calibration measurements required a precise temperature and pressure; also required was that the meter bar be supported at the so-called Airy points, for which bending is minimized.

In 1960 the CGPM introduced a microscopic reference by defining the meter as a specific number of wavelengths of the emission from a transition in krypton-86. Now every laboratory in the world could create their own standard. But the length standard was still tied to a specific atomic transition, and with the development of lasers, krypton was no longer the best choice available. Instead of picking another atomic or molecular line, in 1983 CGPM defined the speed of light as 299 792 458 m/s and the meter as the distance travelled by light in vacuum in 1⁄299 792 458 of a second. In practice, because researchers can measure time and frequency much more accurately than length, they measure any laser’s frequency and then convert it to a wavelength using the speed of light. With a defined $c$, any laser wavelength can serve as a ruler for the meter.

The kilogram’s definition has a history similar to that of the meter. Originally, in 1795 the kilogram was defined as the mass of one liter of pure water at the melting point of ice. But unavoidable impurities in the water limited the precision. Manufactured prototypes were thus developed. In 1799 a cylinder made of platinum was introduced, and in 1879 one made of platinum–iridium, shown in the opening image on page 32, came into use; it provided the definition of the kilogram for 140 years. The problem was that when the original platinum–iridium cylinder, or the urkilogram, and its copies were compared after a year, their masses differed by up to 50 micrograms, likely because atoms fell off or hydrogen was absorbed from air contaminants or cleaning products.

The urkilogram was difficult to replace because microscopic and macroscopic masses differ by a factor of 10²⁵, which is hard to measure accurately; in contrast, the meter is on the order of 10⁶ optical wavelengths. To define the kilogram in a microscopic way, metrologists could have used the mass of a specific number of a specific atom, or of electrons or protons, similar to the meter’s definition in terms of krypton radiation. Instead, the new definition relied on a set value for a fundamental constant, similar to the meter’s definition through the speed of light. For the kilogram, the fundamental constant was Planck’s quantum $h$. Researchers can use many systems and measurement methods to realize the kilogram, as long as the result can be expressed by $h$ and a frequency.

With the new definition of the kilogram, all unit definitions in physics rely on microscopic quantities or fundamental constants and no longer involve manufactured artifacts. Any laboratory in the world can create primary standards; Paris, the home of the meter bar and the urkilogram, has lost its special role.

Kilogram in terms of frequency

Time is central to the SI because it can be measured in terms of frequencies much more precisely than any other quantity. The International Committee of Weights and Measures defines the second as “the duration of 9,192,631,770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the caesium-133 atom”; that is, the Cs hyperfine frequency is defined as 9.192 631 770 GHz. Cesium is a practical choice: Its frequency is convenient, and its heavy mass leads to low atomic velocities and thus to small transit-time spectral broadening. A single photon at the Cs hyperfine frequency ${\nu }_{\mathrm{Cs}}$ has an energy $E=h{\nu }_{\mathrm{Cs}}$, which, through the Einstein relation $E=m{c}^2$, converts into a mass equivalent $m_{\mathrm{ph}}=h{\nu }_{\mathrm{Cs}}/c^2$. The new kilogram definition fixes the relativistic mass of a photon at the Cs hyperfine frequency as $m_{\mathrm{ph}}$ = 6.777 265 × 10⁻⁴¹ kg.

Because total energy is conserved, if a Cs atom absorbs a photon of frequency ${\nu }_{\mathrm{Cs}}$ and transitions to its higher-energy hyperfine state, its mass must increase by $m_{\mathrm{ph}}$. That effect was observable in the mass difference of two isotopes of silicon or sulfur. ³ One isotope transformed into the other by capturing a neutron, but because of the nuclear binding energies, the measured change in mass was smaller than that of the captured neutron. The gamma-ray photons emitted during the process accounted for the apparent loss of mass with a precision of 10⁻⁷. But the Cs microwave photon produces a far smaller change in mass than do the gamma rays emitted in a nuclear reaction.

In the new definition, one kilogram is the mass difference between $c^2/h{\nu }_{\mathrm{Cs}}$ = 1.475 521 4 × 10⁴⁰ Cs atoms in the upper and lower hyperfine states. In theory, a researcher could measure 1 kg of a substance using a mechanical balance with the substance and ground-state Cs atoms on one side and excited-state Cs atoms on the other side, as shown in figure 1a; the mass of the ground-state atoms alone, though, would be 3.26 × 10¹⁵ kg and fill a cube with 12 km sides. That expression for the kilogram is similar to the original 1999 proposal to use a fixed value of $h$ to replace the kilogram artifact: “The kilogram is the mass of a body at rest whose equivalent energy equals the energy of a collection of photons whose frequencies sum to 135,639,274 × 10⁴² hertz.” ⁴

Figure 1.

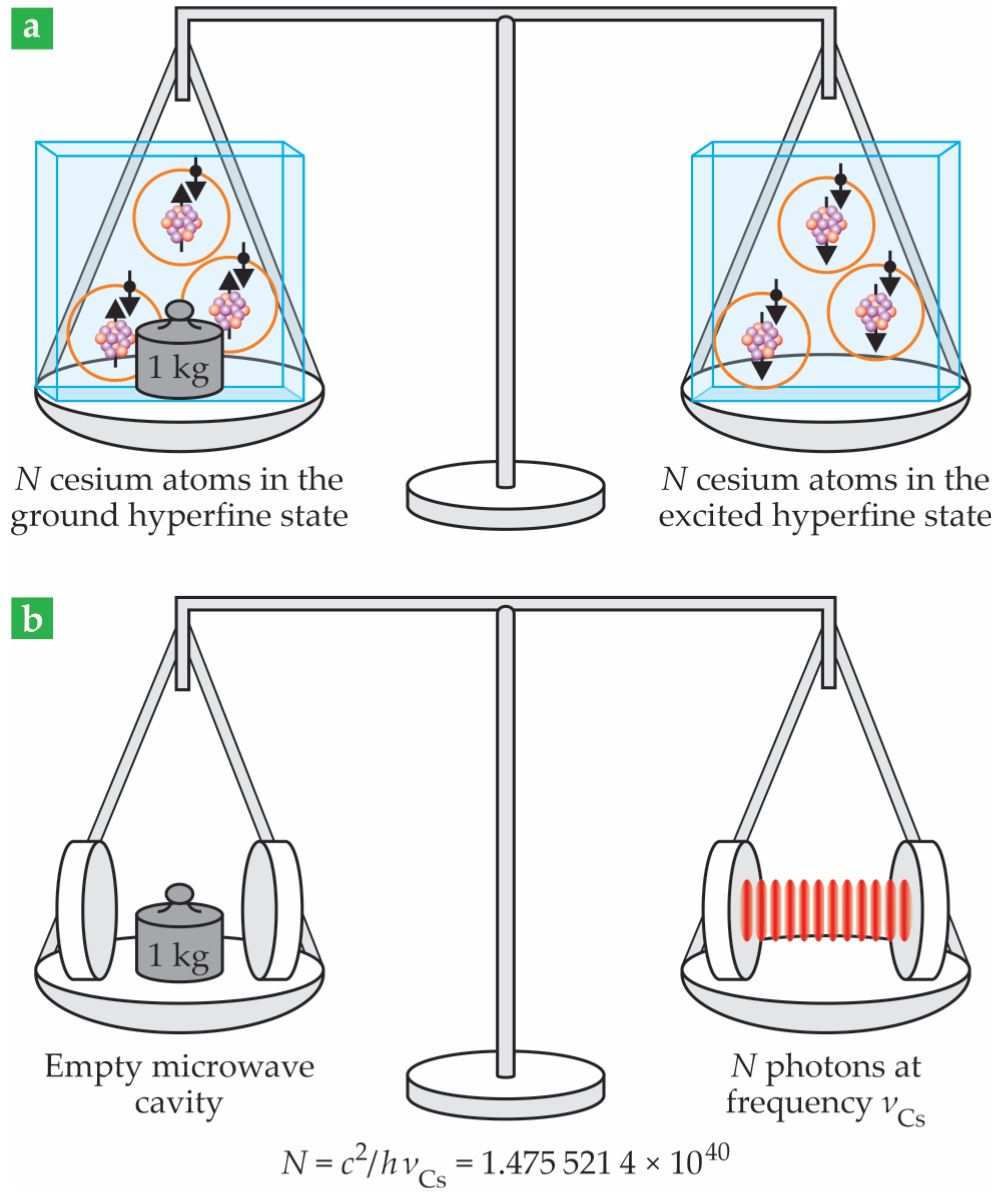
A Cs atom isn’t even necessary to turn a photon’s relativistic mass into rest, or invariant, mass. If photons are in a cavity, their total momentum is zero, and they are at rest in the lab reference frame. The composite rest mass is the mass of the empty cavity plus the photons’ relativistic masses. The kilogram can then be defined as the mass of 1.475 521 4 × 10⁴⁰ photons at ${\nu }_{\mathrm{Cs}}$ stored in a microwave cavity, as shown in figure 1b. But creating one kilogram of pure electromagnetic energy is demanding. Even in a lossless microwave cavity, one kilogram of photons would require pumping the cavity for a full year with about 3 GW of microwave power, the output of a medium-sized nuclear power plant.

The definition above is impractical or even impossible for calibrating masses. But through highly accurate (10⁻²⁰) frequency ratios and frequency combs, researchers can use any radiating system to define the kilogram. As a simple but still impractical example, they could annihilate an electron and a positron to create radiation at a frequency linked directly to the electron mass $m_{\mathrm{e}}$. The process emits two gamma-ray photons of energy $m_{\mathrm{e}}{c}^2$ = 511.0 keV, or frequency ${\nu }_{\mathrm{ep}}$ = 1.2356 × 10²⁰ Hz. The mass of the electron is $m_{\mathrm{e}}=h{\nu }_{\mathrm{ep}}/c^2$ = 6.777 265 × 10⁻⁴¹ kg (${\nu }_{\mathrm{ah}}/{\nu }_{\mathrm{Cs}}$), in terms of fundamental constants $h$ and $c$ and the frequency ratio relative to a Cs clock.

Kilogram through atomic spectroscopy

A kilogram based on gamma rays is not practical, given how difficult it is to measure their frequencies with high precision. So instead of converting the rest energy $m_{\mathrm{e}}{c}^2$ into radiation and measuring its frequency, physicists convert kinetic energy $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.m_{\mathrm{e}}{v}^2$ into more manageable ultraviolet radiation. But they need to know the velocity $v$ very well.

In hydrogen spectroscopy, the electron has a well-known velocity. Besides some small well-understood corrections, the ionization energy of hydrogen is the Rydberg energy $\mathit{Ry}$, which equals the kinetic energy of the 1s electron with velocity $c$ times the fine-structure constant $\alpha$. Through hydrogen spectroscopy and the Cs frequency standard, $\mathit{Ry}$ is known with a precision of nearly 10⁻¹². The fine-structure constant $\alpha$ can also be measured with high accuracy through several independent methods, including the quantum Hall effect, determination of the magnetic moment of the electron, and atom interferometry. Finally, the mass of the electron derives from the equation $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.m{\left(c\alpha \right)}^2=\mathit{Ry}$.

Hydrogen spectroscopy is thus a feasible way to measure the mass of the electron. The experimental realization has a precision of 2 × 10⁻¹² for the Rydberg constant, limited by the uncertainty in the finite size of the proton. ⁵ But how does the mass of the electron define a macroscopic mass? The first step is to relate the mass of the electron to the masses of atoms. An electron and an atomic ion placed sequentially in a Penning trap have cyclotron frequencies $qB/2\pi m$, which depend on their masses, the magnetic field $B$, and their electric charges $q$. The ratio of those frequencies yields the mass ratio ⁶ with a precision of 4 × 10⁻¹⁰.

The International Avogadro Coordination (IAC) project, led by Physikalisch-Technische Bundesanstalt (PTB) in Germany, took the remaining step to convert microscopic to macroscopic mass. The project members used hydrogen spectroscopy and Penning trap mass comparisons to connect ${\nu }_{\mathrm{Cs}}$ to $m_{\mathrm{Si}}$ as described above. (Atom interferometry, described in box 1, provides a more direct connection from ${\nu }_{\mathrm{Cs}}$ to $m_{\mathrm{Si}}$.) To go from $m_{\mathrm{Si}}$ to bulk silicon, they counted the number of silicon atoms in a macroscopic sphere of about 1 kg, as shown in figure 2. One kilogram of silicon has about 2 × 10²⁵ silicon atoms, so counting them, even at 50 million atoms per second, would take about the age of the universe. The solution was to determine the volume per atom and the total volume of the object.

Figure 2.

Atom interferometry

Hydrogen spectroscopy connects the mass of the electron to the hyperfine frequency of cesium by measuring the electron’s kinetic energy in the ground state. For those measurements, small corrections from quantum electrodynamics effects and the finite proton size must be determined by other measurements. Atom interferometry, on the other hand, directly determines the kinetic energy of an atom by a frequency measurement.

In an atomic recoil measurement, a photon transfers to an atom a precise momentum, $p=h\nu /c$, controlled by the photon’s frequency $\nu$. A spectroscopic measurement of the kinetic energy $p^2/2m$ determines the atomic mass. An atom interferometer implements that concept using two photons and kinetic energy measured as the phase shift between two arms of the interferometer, with one path getting a precise momentum kick and the other staying at rest.

A pulse of counterpropagating laser beams (green arrows traveling along the dashed green lines in panel a) at different frequencies places an atom, initially at rest (solid black line) into a superposition of moving and resting states (solid gray lines). A second laser pulse with both beams at the same frequency reverses the direction of the moving arm without disturbing the resting arm. A final pulse, identical to the initial pulse, reads out the arms’ phase difference, which results from the kinetic energy of the moving arm, through the relative populations in the two output ports of the interferometer (dashed black lines).

When an atom scatters a photon from one beam into the other after each pulse, as shown in panel b, it receives a momentum transfer $p$ equal to the sum of the two photon momenta, $p=ħ(k_1+k_2)=h({\nu }_1+{\nu }_2)/c$, where $k_1$ and $k_2$ are the wavenumbers and ${\nu }_1$ and ${\nu }_2$ are the frequencies of the two laser beams. A measurement of that momentum transfer, at least in principle, has the precision of laser-frequency measurements, which are currently limited only by the Cs frequency standard.

After the momentum transfer, an atom initially at rest has a kinetic energy $E_{\mathrm{k}}=p^2/2m$. The stimulated light-scattering process becomes resonant, as it is in panel a, when the kinetic energy equals the difference of the two photon energies, $h({\nu }_1–{\nu }_2)$. If the atom is not initially at rest, the resonance frequency is Doppler shifted, but in most interferometer schemes, the Doppler shift cancels out to leading order. In that way, frequency measurements now directly determine an atomic mass. ¹¹ The most recent atom-interferometry measurement was more accurate than the previous best value of the atomic fine-structure constant $\alpha$, and in combination with hydrogen spectroscopy it provided a new value for $\alpha$. ¹² (Image courtesy of Wolfgang Ketterle and Alan Jamison.)

The IAC researchers started by creating the world’s most perfect sphere out of single-crystal isotopically enriched silicon. They determined the sphere’s diameter $d$ of 9.4 cm with an uncertainty of 0.2 nm through optical interferometry and characterized the surface layer, which contributed about 80 ± 10 µg to the mass. To find the volume per atom, they performed x-ray diffraction on the sphere to determine the lattice constant $a$ with a precision of 2 × 10⁻⁹, which was limited by strain from point defects. Each unit cell has a volume of $a^3$ and contains eight silicon atoms. The total number of atoms in the sphere, then, is $(4\pi /3)d^3/a^3$. The silicon sphere provides a macroscopic mass standard ⁷ with a total uncertainty of about 10 µg or relative precision of 10⁻⁸.

The conceptual definition of the kilogram involved 1.475 521 4 × 10⁴⁰ photons at the Cs hyperfine frequency. Instead of counting 10⁴⁰ photons, the Avogadro project counted approximately 10²⁵ silicon atoms. The mass of a silicon atom is 15 orders of magnitude larger than the relativistic mass of a Cs photon. Those additional 15 orders of magnitude come in roughly equal factors from comparing frequencies $\left(\right(\mathit{Ry}/h)/{\nu }_{\mathrm{Cs}})$, comparing masses $(m_{\mathrm{Si}}/m_{\mathrm{e}})$, and using ${\alpha }^{-2}$ for the ratio of the electron’s rest energy ($m{c}^2$) and kinetic energy in the hydrogen ground state.

Kibble balance

A final method to realize a mass standard is the Kibble balance, formerly called the Watt balance. Until 2019 the Kibble balance was used to measure the value of Planck’s constant $h$. After the new SI unit definitions with the fixed numerical value of $h$, it became a method to calibrate the kilogram with a precision on the same order as the silicon spheres. Box 2 gives the standard explanation of the Kibble balance, but a conceptual explanation compares it with the other methods.

Kilogram with the Kibble balance

In the main text, the concept of the Kibble balance is explained through energy conservation: The electrical power required to levitate an object of mass $m$ at velocity $v$ is equal to the rate of change of mechanical energy, $mvg$. But the Kibble balance measures virtual rather than real power to eliminate contributions from friction and ohmic dissipation. To do so, it operates in two modes.

In force mode (panel a in the figure), the Kibble balance magnetically levitates the test object. The Lorentz force $F_{\mathrm{L}}=ILB$ equals the weight $F_{\mathrm{m}}=mg$, where $I$ is the current through the solenoid, $L$ is the length of the solenoid conductor, and $B$ is the external radial magnetic field.

In velocity mode (panel b), the Kibble balance moves the solenoid at a constant velocity $v$. When the coil is lowered by an amount $\Delta z$, a magnetic flux of $BL\Delta z$ leaves the solenoid. By Faraday’s law, the change in magnetic field induces a voltage $U$ in the solenoid’s open loop equal to $LBv$, the time derivative of the magnetic flux.

With the current measured in force mode and the voltage measured in velocity mode, their product $IU=mvg$ is independent of the quantities $B$ and $L$, which are difficult to measure. The result is the same as discussed in the main text, that electrical and mechanical power are equal, but now in terms of virtual powers. (Image courtesy of Bureau International des Poids et Mesures.)

The basic idea is to measure a change in mechanical energy, which is proportional to the mass of an object, using electrical power. When a motor lifts an object with velocity $v$ in a gravitational field, the mechanical power $P=mgv$ must equal the electrical power $P=IU$, in terms of current $I$ and voltage $U$. In a process similar to that of atomic spectroscopy or atom interferometry, researchers determine the mass of a now-macroscopic object with well-known velocity and acceleration from the mechanical energy. They measure $v$ and $g$ precisely by forming a Michelson interferometer with the object serving as one mirror.

In the Kibble balance, the motor is replaced by a levitating coil with current $I$ in a magnetic field. The current is adjusted until the magnetic force on the coil compensates for the gravitational force on the object—that is, until the object is levitated. With no extra mechanical force, the object’s gravitational potential energy can be increased at a rate $mgv$. To conserve energy, the power $P=mgv$ must come from electrical power.

Researchers use the Josephson effect to measure the product of voltage and electron charge, $eU$. When a DC voltage is applied to a tunnel junction between two superconductors, it creates a current oscillating at the Josephson frequency ${\nu }_{\mathrm{J}}=2eU/h$, which can be measured precisely. The factor of two appears in the equation because superconducting currents are carried by electron pairs with a charge of $2e$. In Josephson voltage standards, microwaves are applied to the junction, and the current–voltage plot shows quantized jumps in voltage steps given by the equation above.

Single-electron pumps operate with currents up to 100 pA at frequencies ⁸ near 1 GHz and count the macroscopic number of electrons per time, $ṅ$, where $I=ṅe$. Combined with the Josephson frequency relation, the electrical power becomes $P=IU=h{\nu }_{\mathrm{J}}ṅ/2$ and depends on a frequency measurement and the counting of electrons.

With electrical power measured that way, the Kibble balance realizes masses by obtaining the energy, or voltage times $e$, of an electron through a frequency measurement, as in the atomic spectroscopy technique, and by counting electrons, similar to counting silicon atoms in the Avogadro project. Although the Kibble balance method is an electrical measurement, it doesn’t need $e$ (which has a fixed value in the new SI units) or any electrical units.

The accuracy of current standards based on single-electron-pumps ⁸ is around 10⁻⁷, so researchers chose a different way to measure the current. It passed through a quantum Hall device kept at a resistance plateau equal to the von Klitzing constant $R_{\mathrm{K}}=h/e^2$, a newly defined quantity of 25 812.807 Ω. The voltage $U=I{R}_{\mathrm{K}}$ is measured by the Josephson effect, and the electrical power becomes the product of two Josephson frequencies and $h$. With the quantum Hall effect, researchers no longer need to count a macroscopic number of particles. Microscopic and macroscopic physics are not connected by counting but by a macroscopic quantum effect.

The new definition of the kilogram has the advantage not only that it can be realized everywhere in the world, independent of artifacts, but also that it can be directly applied to objects at any mass. For a 1 kg object, the precision of the Kibble balance and silicon spheres is about the same as the urkilogram. But for smaller masses, the old definition required dividing masses using pairwise comparisons of equal masses, and each order of magnitude typically involved five weights. ² Reaching milligrams, for example, required many steps with huge losses in precision, whereas the new definition works the same for a kilogram or a milligram.

The various routes to the new kilogram can be reduced to connecting a frequency to the mechanical or relativistic energy of a particle. Conceptually, that means using the relativistic energy of a particle (through annihilation radiation). Practically, it means using the kinetic energy of a microscopic object with either a well-known velocity (electron in the hydrogen atom) or momentum (atom interferometry) or of a macroscopic object with well-known velocity and acceleration (Kibble balance).

Planck units

The new SI units almost reach Max Planck’s 1899 vision to define all units using only fundamental constants without reference to specific particles. ⁹ Planck suggested defining the gravitational constant $G$, which would then define the mass in Planck units, or Planck mass, $m_{\mathrm{P}}=\sqrt{\hslash c/G}$. Although used widely in particle-physics theory, the Planck mass is not a practical way to define units, given that $G$ is currently the fundamental constant with the largest relative uncertainty by far (2 × 10⁻⁵). But how, in principle, could Planck’s suggestion be implemented?

First, what is the Planck mass? If the mass of a point-like object increases, its reduced Compton wavelength $ħ/mc$ becomes shorter, whereas the Schwarzschild radius $2Gm/c^2$—the event horizon of the black hole created by the point particle—becomes larger. Those two lengths are the same when the object has the mass $m_{\mathrm{P}}/\sqrt{2}$.

To measure masses in units of the Planck mass, a gravitational effect must be measured at some distance $r$. That distance can be in units of the reduced Compton wavelength ${ƛ}_0=\hslash /\left(m_{0}c\right)$ of a suitable reference particle of mass $m_0$. The simplest gravitational effect is Newtonian acceleration $g=Gm/r^2$, which can be written as $\tilde{g}={(m/m_{\mathrm{P}})}^2(m_0/m)/{\tilde{r}}^2$ in units of the speed of light per Compton time, or $c^2/{ƛ}_0$, and the length $\tilde{r}$ in units of ${ƛ}_0$. The mass $m$ is then in units of the Planck mass through measurements of a mass ratio $m_0/m$, a length ratio $\tilde{r}$, and the acceleration $\tilde{g}$ using ${ƛ}_0$ as a ruler. Currently, no precise methods exist to measure the mass ratio between a large object, for which gravity can be observed, and a microscopic reference particle.

A more elegant but equally unrealistic method is the gravitational redshift $\delta \nu /\nu$. In the weak-gravity limit, the redshift is proportional to the gravitational potential and given by $Gm/\left(r{c}^2\right)$. The redshift becomes $\delta \nu /\nu ={(m/m_{\mathrm{P}})}^2(m_0/m)/\tilde{r}$, and masses in units of the Planck mass are determined by ratios of mass, frequency, and length.

Unlike Planck’s vision, the new SI units still use one specific particle, the cesium atom, although that unique role will soon likely pass to another atom with an optical frequency, such as strontium, ytterbium, ytterbium ions, or aluminum ions. ¹⁰ Planck argued that the selection of an atom and a spectral line to define frequency is arbitrary, whereas definitions based on fundamental constants would be valid for all times and all cultures, including extraterrestrial and extrahuman cultures (“ausserirdische und aussermenschliche Culturen”). ⁹

Planck’s units and the new SI units could, in principle, be fundamentally different. For example, if the expectation value of the Higgs field slowly changes as a function of position, the masses of elementary particles would subtly alter, but fundamental interactions would remain unchanged. SI units based on a selected particle would then drift in value from place to place, whereas the Planck units would remain fixed. That example illustrates one of the many connections between metrology and fundamental science.