Tip of the iceberg

The phrase “tip of the iceberg” suggests that what you see is much less than what is hidden from view. The concept of a tip above seawater and a much larger root below more or less conforms to Archimedes’s principle of buoyancy: The force exerted on a body partially or completely immersed in a fluid of higher density is directed upward and is equal to the weight of the fluid that the body displaces.

When a totally submerged lower-density body is released, the buoyancy force causes it to rise until it reaches a floating equilibrium. The tip then rests above the surface and the root below it, with the mass of each determined by the density contrast between the floating solid and the surrounding fluid. Figure 1 depicts a common representation of such an equilibrium. But the configuration is pure artistic license—it does not display a stable orientation and does not exist in nature.

Figure 1.

Sphere, cube, and cylinder

What’s wrong with the image? A floating elongated iceberg can satisfy the buoyancy requirements of Archimedes’s principle in many orientations, but most, including that depicted in figure 1, turn out to be unstable. To see an example of such an instability, take a wine cork and immerse it in water in any orientation. Upon release, the cork will rise to the surface and float only with its long axis horizontal—that is, parallel to the surface of the water.

An equilibrium orientation of a floating body occurs when the center of gravity (the center of mass of the whole object) and the center of buoyancy (the center of mass of just the submerged part) are vertically aligned. If perturbations from wind, waves, or melting lead to a small departure of that alignment, a torque is created that reorients the body. If the torque amplifies the misalignment, the orientation is unstable; if the torque reduces the misalignment, the orientation is stable.

What are the parameters that define a stable equilibrium orientation? A floating object must satisfy Archimedes’s principle by displacing a mass of fluid equal to its own. Because the object is less dense than the underlying fluid, it projects some volume above the surface and some volume below. Thus the first parameter that determines the stable equilibrium is the density contrast between the floating body and the surrounding fluid, here defined as a ratio $\rho$ of the two densities, with $0<\rho <1$.

The density of ocean water depends on both temperature and salinity; the density of ice depends on ambient temperature and the concentration of bubbles and structural voids. But an ice–water density ratio of $0.90$ is accurate enough to characterize the stability of ice objects afloat in the ocean. It is behind the tip-of-the-iceberg concept because at typical densities of the two phases, about 90% of an iceberg’s volume is submerged, leaving only the tip above water.

The second important parameter is the shape of the floating body. Consider a floating sphere. Once its fractional volumes above and below the fluid surface have been established by the density contrast, it will float stably in any orientation. But a cubic body has well-defined stable orientations relative to the fluid surface that over a wide range of densities do not include the intuitive orientations—floating with a face or edge parallel to the fluid surface or with a corner pointing upward, perpendicular to the surface. To test that assertion experimentally, just place a cube of wood in water and let it stabilize.

How will an iceberg shaped like the one shown in figure 1 establish a stable equilibrium orientation? A geometry useful for examining stability quantitatively is the circular cylinder of length $H$ and diameter $D$, as shown in figure 2. When $H<D$, the cylinder is a disk, and when $H>D$, the cylinder is elongated, like a wine cork or pencil. The question raised by figure 1 is whether cylindrical bodies of ice whose lengths exceed their diameters float with their long axes perpendicular to the water surface? The answer is generally no, particularly for elongated cylinders with $H>2D$.

Figure 2.

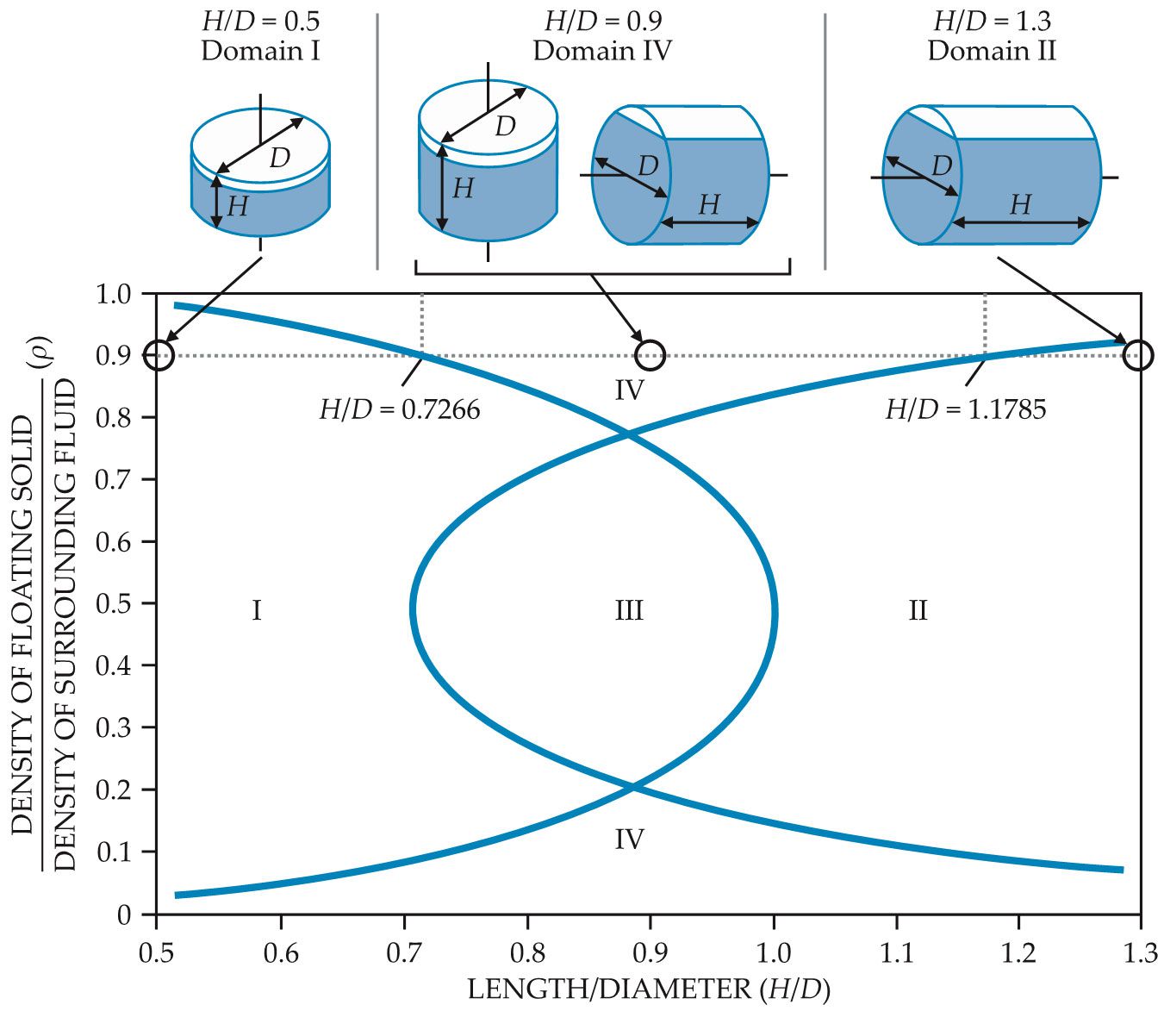
The shape of stability

In 2004 D. S. Dugdale presented a useful discussion of the floating-cylinder problem. He defined four domains of stable equilibrium in density–shape space: (I) The cylinder floats with its rotational axis perpendicular to the water surface and its circular faces parallel to the water surface. (II) The cylinder floats with its rotational axis parallel to the water surface and its circular faces partially submerged to a depth dependent on the density of the cylinder. (III) The rotational axis of the cylinder is tilted at an angle neither parallel nor perpendicular to the surface. (IV) The orientations described in I and II are both stable.

Figure 2 illustrates the complexity of those domains of stable equilibrium as a function of density contrast and cylinder shape. For ice floating in water ($\rho =0.9$), stable equilibria exist only under the conditions of domains I, II and IV; the density conditions that yield stable equilibria within domain III (that is, in the range $0.2<\rho <0.8$) exclude the ice–water density contrast. Therefore, ice cylinders floating in water will stabilize in only two orientations—with the cylindrical axis either perpendicular or parallel to the water surface.

In 1991 Edgar Gilbert showed that for a stable equilibrium with the cylindrical axis perpendicular to the water surface, the following condition must hold: $\rho (1-\rho ){(2H/D)}^2<0.5$. For $\rho =0.9$, the equation requires that $H/D<1.1785$. A glance at the iceberg in figure 1 leaves little doubt that its $H/D$ ratio is greater than that. So the iceberg violates the stability condition required for the cylinder to float with its rotational axis perpendicular to the water surface. It would therefore spontaneously reposition itself to an orientation with its rotational axis horizontal. In that equilibrium orientation, the waterline on the cylinder is a rectangle of length $H$ and width $w$.

The width is determined by the density difference between the floating body and the fluid—that is, by how much of the cylinder is submerged. Gilbert showed that the equilibrium is stable if $w<H$. For $\rho >0.5$, $w<D$, and all cylinders where $H/D>1$, the condition for stability is met because $w<D<H$. The actual stability field, as determined from the condition $w<H$, is $H/D>0.7266$, as shown in figure 2. Therefore, along the dashed line $\rho =0.9$ and in the range $0.7266<H/D<1.1785$, both cylinder orientations are stable and can coexist. For $H/D>1.1785$, certainly the case for the iceberg in figure 1, the equilibrium orientation is intrinsically unstable and does not occur in nature.