The no-cloning theorem
DOI: 10.1063/1.3086114
The principle of superposition is a cornerstone of quantum mechanics. It says that when two evolving states solve the SchröUdinger equation, any linear combination of the two is also a solution. For that reason, waves from the two slits in the double-slit experiment simply add together to create the familiar interference pattern. As it happens, the superposition principle also prohibits the arbitrary copying of quantum states.
Linearity, unitarity, and cloning
To see why, imagine a machine that copies the state of a photon or an electron. When the original enters, two copies come out, each having the same state as the original. If such a machine were successful, it would convert the state |




















The difficulty stems from the inherent nonlinearity of copying: When one asks for “two of the same,” a square |s〉|s〉 of the original |s〉 is requested. The desire for a squared state is in conflict with the strict linearity of quantum theory. As a result, a single cloner cannot make a perfect copy of every quantum state. So what states can it clone?
Thus far, we have considered the linearity of quantum mechanics. But quantum evolutions preserve probability. The norm 〈e|e〉 of the state emerging from the copier must be the same as 〈s|s〉 of the original. The only difference between the two norms, expressed in terms of |








One reaches the same conclusion after recognizing that quantum evolutions are unitary—they preserve the scalar product of any two states. So for states that can be copied, one again gets 〈




Quantum evolutions are reversible, so one can imagine running the copier in reverse to delete the extra copy in states such as |




The optimistic assumption that a copier will work according to specs for the arbitrary states |



In sum, one cannot make a perfect copy of an unknown quantum state, since, without prior knowledge, it is impossible to select the right copier for the job. That formulation is one common way of stating the no-cloning theorem.
Quantum cryptography
The impossibility of cloning may seem at first an annoying restriction, but it can also be used to one’s advantage—for instance, in a quantum key distribution scheme devised by Charles Bennett and Gilles Brassard in 1984. The idea is for the sender, Alice, to transmit many photons to the receiver, Bob, with the aim of ultimately creating a shared, secret, random string of zeros and ones. Such a random string can later be used as a key for encrypting and decrypting messages. For example, armed with a coded binary message and the key, Bob can decode the message by reversing the binary ciphers in all the positions where the key has a “1.”
In the Bennett-Brassard scheme, each of Alice’s photons is prepared at random in one of four possible polarization states: 

Although Eve cannot perfectly copy the photons Alice sends to Bob, she can, in fact, do a pretty good job of approximately cloning Alice’s transmission. Indeed, optimal approximate cloning is, in principle, one of the best methods Eve can use against quantum cryptography. Fortunately for Alice and Bob, it is possible to place strict theoretical limits on the fidelity of any such copying scheme. The study of approximate cloning is currently an active area of both theoretical and experimental research and is discussed in detail in the additional resources provided at the end of this Quick Study.

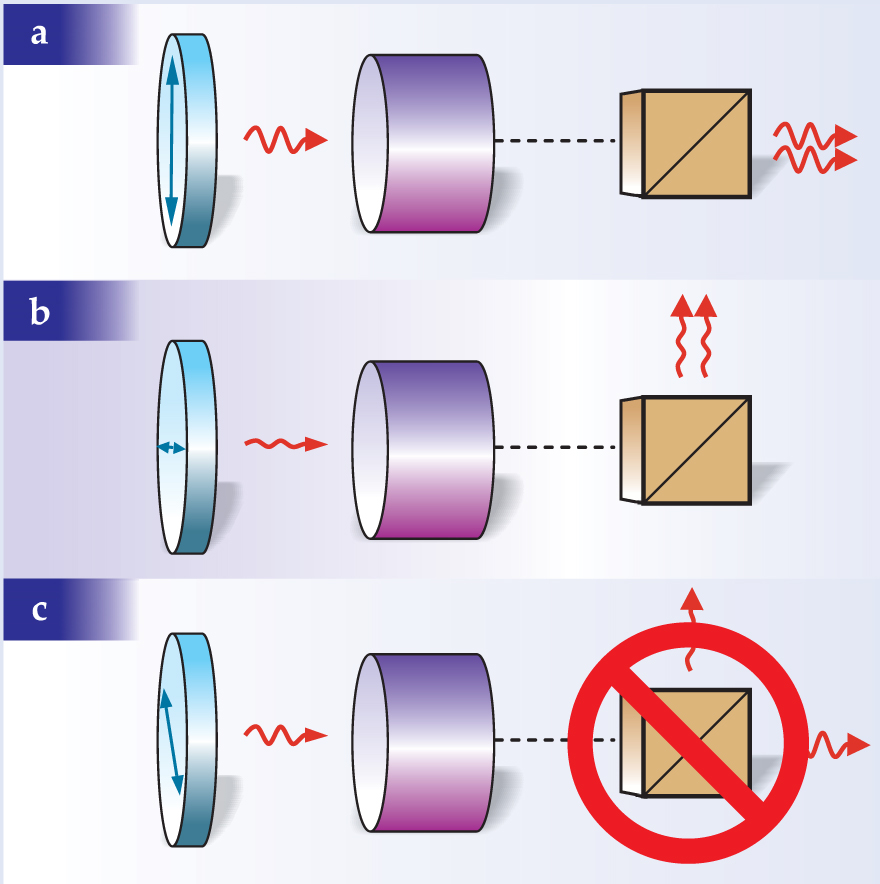
There is no perfect quantum copier. Imagine a device that could clone an arbitrary quantum state. (a) A vertically polarized photon would yield two vertically polarized photons, both of which make the “vertical” choice at a polarizing beamsplitter. (b) A horizontally polarized photon would yield two horizontally polarized photons, both of which make the “horizontal” choice. (c) Because quantum mechanics is linear, a diagonal polarization—a superposition of vertical and horizontal—can produce only the measurement outcomes represented in panels a and b; it could not produce the outcome shown. But such an outcome would be possible if the diagonal polarization were cloned correctly. The linearity of quantum mechanics thus prohibits the cloning of arbitrary states.
Causality, copying, and collapse
If cloning were possible, one could communicate instantaneously over a distance. Suppose Alice and Bob share two photons in the entangled polarization state, 


In view of the collapse induced by Alice’s measurement, Bob’s photon, in a sense, gets the message. But Bob doesn’t. He cannot simply ask his photon, “What’s your state?” A quantum measurement is a multiple-choice test. It poses questions such as, “Are you |↕〉 or |↔〉?” Eigenstates of the measured observable are the only legal answers. If he wrongly measures in the basis complementary to that selected by Alice, Bob will randomize the state of his photon and, in effect, erase Alice’s message. And to choose correctly, he needs to know the message. That’s the proverbial Catch-22.
Direct measurement fails, but what if Bob were able to clone his photon first? Copying 

What if Bob uses a copier for, say, just the basis {|↕〉, |↔〉}? If Alice sends “0,” the copier works. But for the diagonal input states (|↕〉 ± |↔〉)/
Nevertheless, the redundancy in states like (|↕↕↕…〉 ± |↔↔↔…〉)/
Phrases like “Bob’s photon gets the message” or “Bob erases the message” suggest that a definite underlying pure state of Bob’s unobserved photon exists as soon as Alice makes her measurement. Such language is natural in that it provides a convenient picture that agrees with experimental results. However, the fact that an unknown quantum state cannot be discovered by a measurement or revealed by cloning suggests that not only is it unknown, but it does not even exist in the usual sense. Indeed, the nature of a quantum state is still the subject of lively debate, and the restriction on copying expressed by the no-cloning theorem is an important part of the discussion.
References
1. V. Bužek, M. Hillery,“Quantum Copying: Beyond the No-Cloning Theorem,” Phys. Rev. A 54, 1844 (1996)
2. V. Scarani, S. Iblisdir, N. Gisin, A. Acín,“Quantum Cloning,” Rev. Mod. Phys. 77, 1225 (2005).https://doi.org/10.1103/RevModPhys.77.1225
3. N. J. Cerf, J. Fiurasek,“Optical Quantum Cloning—A Review,” Prog. Opt. 49, 455 (2006).https://doi.org/10.1016/S0079-6638(06)49006-5
More about the authors
Bill Wootters is a professor of physics at Williams College in Williamstown, Massachusetts. Wojciech Zurek is a laboratory fellow in the theoretical division of Los Alamos National Laboratory in New Mexico.
William K. Wootters, 1 Williams College, Williamstown, Massachusetts, US .
Wojciech H. Zurek, 2 Los Alamos National Laboratory, New Mexico, US .




