From cracks to atoms and back again

Something usually seems real only when we can detect it with our own senses. The famous 1972 photograph of Earth as a blue marble rising above the Moon is a dramatic case in point. It makes our planet appear round in a vivid way unseen before.

What, then, can we make of atoms, which will always be too small to see with ordinary visible light? The speculation that matter is made of atoms goes back millennia to Lucretius’s De Rerum Natura (On the Nature of Things). Compelling scientific evidence is not that old, but it does go back centuries to an unexpected corner of physics—the fracture of solids—where the influence of atoms, if not the atoms themselves, is visible.

Cleaving crystals

Fracture is the process by which external forces break a solid object into pieces. It can happen in any solid but is most suggestive as it occurs in crystals. Many of those types of stones have translucent optical properties that make them precious or semiprecious and produce fractures with flat surfaces. Jewelers can cleave them into appealing symmetrical shapes, a process that happens because crystal faces form only at specific angles to one another.

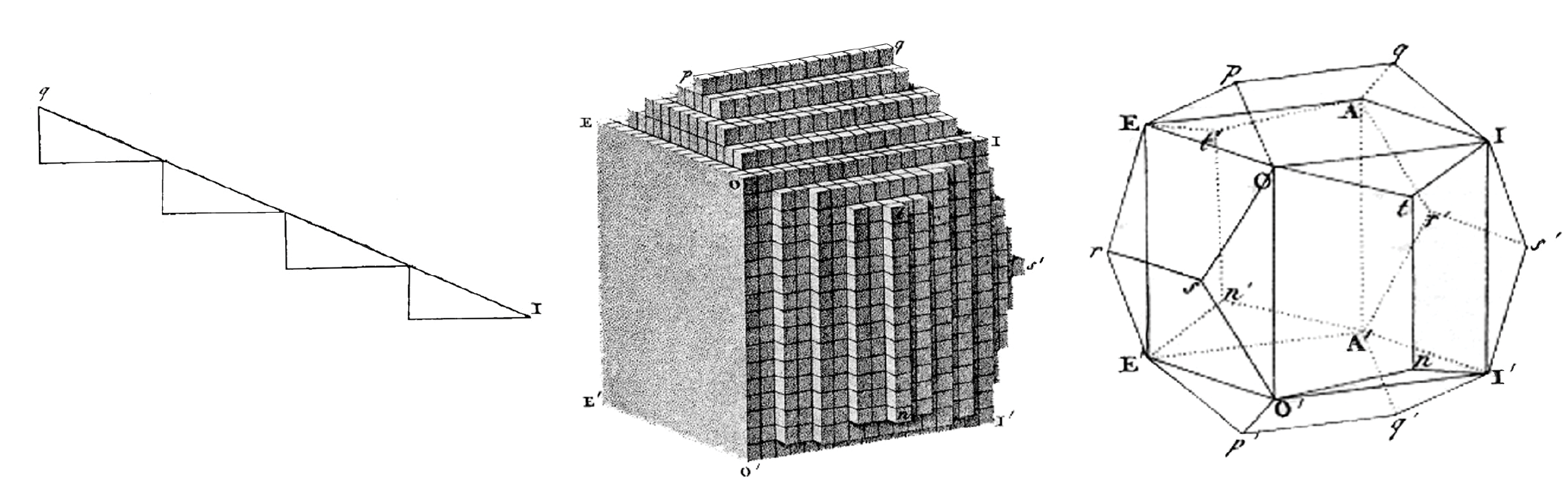
The cleaving occurs only along invisible natural joints inherent in each crystal. In the late 18th and early 19th centuries, the French mineralogist René Just Haüy imagined that crystals are built from vast numbers of identical cells, from which the faces emerge as stepped surfaces. For example, a surface that goes sideways two units and upward one unit will form an angle 26.5° above the horizontal, as shown in the left panel of the figure.

Haüy’s struggle to explain fracture opened a winding intellectual path that led over the next hundred years to an understanding of matter as being composed of atoms. But scientists were slow to take up the question of how to explain fracture itself. The first modern study was published in 1920 by the British engineer Alan Arnold Griffith, who examined the strength of glass fibers as their diameters decreased. The stress needed to break them increased the thinner the fibers became, and from that trend he deduced that the breaking stress is inversely related to the depth of the largest crack on their surface. He also focused on the fact that energy is required to break the bonds when cleaving a surface, and a crack can advance only if energy is available.

Griffith had annoyed his superiors at the Royal Aircraft Establishment at Farnborough by doing experiments on glass rather than on aluminum and other practical materials that would help ensure the safety of airplanes. He also had the misfortune of setting his laboratory on fire one night. Thus he was ordered to stop work on glass after 1920.

Three decades later the UK’s de Havilland Aircraft Company produced the world’s first commercial jetliner, and not long into service several planes fell mysteriously from the sky. The line of investigation Griffith had begun was exactly what was needed to understand why, but by the time the significance of his work became fully apparent, leadership in both the study of fracture and the manufacture of jet airplanes had moved across the Atlantic Ocean to the US.

Concentrated stress

The key person at the forefront of fracture science in the US was George Rankin Irwin. Although his first degree was in English, he obtained a PhD in physics from the University of Illinois in 1937 and then went to work at the US Naval Research Laboratory. During World War II, he began to investigate the fracture of steel. The US Navy needed additional insight into the topic to build armor and to stop the phenomenon of new all-welded ships, which had been built in haste for the war, sometimes cracking in half on launch.

Starting in 1948 Irwin developed a new theory for fracture. He began with Griffith’s observation that cracks need energy to move and then asked how that energy flowed. When a cracked solid is under tension, energy stored inside it spontaneously runs to the crack tip, like water in a pool rushing into a drain. At the tip, it creates a stress concentration that is strong and sharp enough to cut atoms apart. The detailed mathematical theory shows that in the vicinity of the crack tip, stress and strain fields take a universal form, rising as one over the square root of distance to the crack tip. The coefficient of that universal stress configuration is called the stress intensity factor.

In brittle crystals, severe material disruption ahead of the crack is limited to distances of a few atomic lengths. If you notch a silicon crystal along one of its planes and pull on it gently, it will come apart. The slight resistance you feel is literally a line of atomic bonds unzipping. The great brittleness makes silicon a poor structural material.

To make structures that endure, builders tend to use materials such as steel, in which an approaching crack tip is disruptive over much larger length scales than in silicon. Driving the crack tip forward in steel requires the metal to flow plastically—that is, to move in a way that’s more fluidlike than solidlike.

At macroscopic scales, however, Irwin’s theory for energy transfer still applies; the stress falls off away from the crack tip in universal inverse-square-root fashion. That way of thinking about fracture unified the study of cracks of many types and paved the way to the engineering study of fracture mechanics.

It took until the 1960s for Irwin’s view of fracture to be accepted: At a 1997 symposium dedicated to Irwin, H. P. Rossmanith said, “It was necessary to overcome a substantial amount of unsympathetic reaction.” Paul Paris, a graduate student at Lehigh University in the late 1950s, studied Irwin’s theories while working in the summer at Boeing, just in time for the engineers there to develop its first civilian jet. Paris proposed a now-classic theory on how cracks creep forward in vibrating structures. It was rejected so many times from journals that Paris eventually placed it in a student engineering magazine. By the end of the 1960s, the whole theory of fracture was placed on a rigorous footing by James Rice—working at Brown University at the time—and other applied mathematicians, and it became a standard part of the engineering curriculum.

A contemporary perspective

Fracture continues to present physics with fascinating scientific questions. Two examples of recent work make the case. Yael Klein and Eran Sharon conducted experiments in thin strips of gel at the Hebrew University of Jerusalem. Because the material is both brittle and floppy, they found that it can undergo a transition that had never before been observed. Sometimes a seed crack runs through the strip. But under slightly different stress conditions, the strip responds by buckling out of the plane instead.

Studying that transition has led scientists to create a new theoretical framework in which to view cracks, where a crack is represented as a line distribution of internal buckling (see my article with Robert Deegan and Eran Sharon, Physics Today, February 2007, page 33 ). The new theory complements the more familiar representation of a crack as a line distribution of stress monopoles called dislocations.

Irwin’s theory postulates that cracks cannot run faster than sound because its speed sets fundamental limits on transporting energy to the crack tip. One can solve the problem of crack motion in crystals analytically, however, and those calculations say that cracks can travel at any speed set by the strain level, so long as the strain is big enough and the crack is not allowed to branch. Supersonic cracks in tension were seen 20 years ago in rubber, but it was thought a peculiarity of that material. New experiments by Jay Fineberg and collaborators in brittle gels are also finding cracks that travel faster than sound. They are trailed by Mach cones at a speed set by the strain level, giving evidence that the predictions from calculations in crystals are correct.

Fracture is a phenomenon that helped atoms seem real, for the fracture of crystals could not be explained without them. Fracture links the macroscopic and microscopic worlds like no other mechanical process, and in doing so continually leads—literally—to scientific breakthroughs.